12.8: El Mecanismo Michaelis-Menten
- Page ID
- 72466
El mecanismo Michaelis-Menten (Michaelis & Menten, 1913) es uno que siguen muchas reacciones mitigadas por enzimas. El mecanismo básico involucra una enzima (\(E\), un catalizador biológico) y un sustrato (\(S\)) que deben conectarse para formar un complejo enzima-sustrato (\(ES\)) para que el sustrato se degrada (o aumente) para formar un producto (\(P\)). La reacción general es
\[S \rightarrow P\]
Y el sencillo mecanismo de dos pasos viene dado por
\[E + S \ce{<=>[k_1][k_{-1}]} ES \label{step1}\]
\[ ES \xrightarrow{k_2} P \label{step2}\]
Observe que la enzima es necesaria para que la reacción continúe, pero no forma parte de la estequiometría general (¡como es el caso de cualquier catalizador!).
Derivación de aproximación de equilibrio
Aplicando la aproximación de equilibrio al primer paso
\[ k_1[E][S] \approx k_{-1}[ES] \label{equil}\]
Y usando una relación de conservación de masa sobre la enzima (señalando que la enzima debe estar en su forma desnuda (\(E\)) o complejada con un sustrato (\(ES\))):
\[ [E]_o = [E] + [ES]\]
o
\[[E] = [E]_o - [ES]\]
Sustituyendo esto en la expresión de equilibrio (Ecuación\ ref {equil}) rinde
\[ k_1([E]_o - [ES])[S] = k_{-1}[ES] \]
Resolviendo esta expresión para revelaciones\([ES]\) paso a paso
\[ k_1[E]_o[S] - k_1[ES][S] = k_{-1}[ES] \]
\[ k_1[E]_o[S] = k_{-1}[ES] + k_1[ES][S]\]
\[= (k_{-1} + k_1 ) [ES]\]
\[\dfrac{k_1[E]_o[S]}{k_1[S] + k_{-1}} = [ES]\]
Sustituyendo esto en la expresión por la tasa de producción del producto\(P\)
\[\dfrac{d[P]}{dt} = k_2[ES] \label{step3}\]
rendimientos
\[\dfrac{d[P]}{dt} = \dfrac{k_2 k_1 [E]_o [S]}{k_1[S] + k_{-1}}\]
Multiplicar la parte superior e inferior de la expresión en el lado derecho por 1/k 1 da el resultado
\[\dfrac{d[P]}{dt} = \dfrac{k_2[E]_o[S]}{[S] + \frac{k_1}{k_{-1}}}\]
La relación de k -1 /k 1 es la constante de equilibrio que describe la disociación del complejo enzima-sustrato,\(K_d\) en la Ecuación\ ref {paso1}. Observando\(k_2[E]_0\) que da la tasa máxima (\(V_{max}\)), y t hat\(\dfrac{d[P]}{dt}\) i s la velocidad de reacción observada, la ley de velocidad toma la forma
\[\text{rate} = \dfrac{V_{max}[S]}{K_d+[S]}\]
Esto se debe a que la velocidad máxima de reacción se logra cuando [ES] es baja. A medida que aumenta [ES], la probabilidad de que el complejo se descomponga para reformar los reactivos es mayor, lo que ralentiza la conversión. [ES] será baja si la concentración de la enzima es mucho mayor que la del sustrato, por lo que nunca hay escasez de enzima disponible para formar el complejo con el sustrato. Sin embargo, si la concentración de sustrato es mayor, la falta de sitios activos enzimáticos disponibles ralentizará la reacción y provocará que se convierta en el orden 0.
En el límite de que la concentración de sustrato es grande en comparación con\(K_d\) (es decir,\(K_d + [S] \approx [S]\)), la reacción termina en orden cero en sustrato.
\[\text{rate} = \dfrac{V_{max}[S]}{K_d+[S]} \approx \dfrac{V_{max}\cancel{[S]}}{\cancel{[S]}} = V_{max}\]
De ahí que agregar más sustrato al sistema bajo esta condición limitante no tendrá ningún efecto sobre la tasa observada. Esto es característico de un cuello de botella en el mecanismo, lo que sucedería si hay escasez de sitios enzimáticos a los que se pueda adherir el sustrato.
En el otro extremo, en el que\(K_d\) es muy grande en comparación con la concentración de sustrato (es decir,\(K_d + [S] \approx K_d \)), la reacción se convierte en primer orden en sustrato.
\[ \text{rate} = \dfrac{V_{max}[S]}{K_d+[S]} \approx \dfrac{V_{max}[S]}{K_d} = \dfrac{V_{max}}{K_d}[S]\]
Derivación de aproximación en estado estacionario
En una derivación alternativa (Briggs & Haldane, 1925) utilizando la aproximación en estado estacionario aplicada al complejo enzima-sustrato
\[\dfrac{[ES]}{dt} = k_1[E][S] - k_{-1}[ES] - k_2[ES] \approx 0\]
Resolviendo para\([ES]\) da el resultado
\[ES] = \dfrac{k_1[E][S]}{k_{-1} + k_2}\]
o
\[[ES] = \dfrac{[E][S]}{K_m}\]
donde
\[K_m = \dfrac{k_{-1}+K_2}{k_1}\]
\(K_M\)es la constante de Michaelis, la cual se ve afectada por una serie de factores, incluyendo el pH, la temperatura y la naturaleza del sustrato mismo. Procediendo como antes, aunque la conservación de la relación de masa y la sustitución en la expresión de tasa (Ecuación\ ref {paso3}) da como resultado
\[\dfrac{d[P]}{dt} =\dfrac{V_{max}[S]}{K_m + [S]}\]
La ventaja de este enfoque es que da cuenta de la pérdida de\(ES\) complejo por la producción de productos así como de la descomposición para reformar los reactivos E y S. Como antes, en el límite de que\([S] \gg K_M\), la reacción alcanza su velocidad máxima (\(V_{max}\)) y se vuelve independiente de cualquier concentraciones. Sin embargo en el límite que\([S] \ll K_M\), la reacción se convierte en 1 er orden en\([S]\).
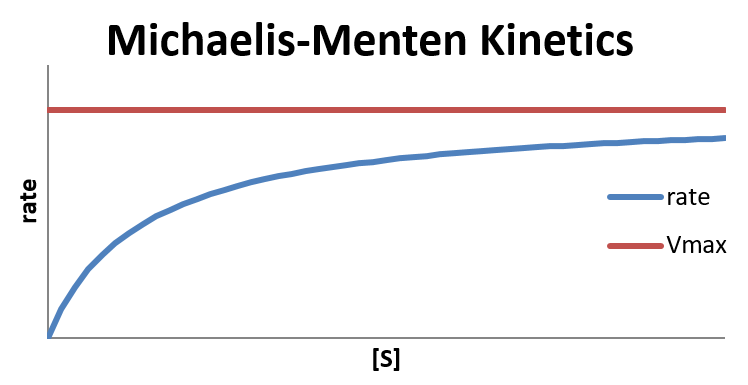
Los parámetros constante de Michalis y V max se pueden extraer de varias maneras. En el método Lineweaver-Burk (Lineweaver & Burk, 1934), se utiliza el recíproco de la ley de tasas para crear una relación lineal.
\[ \dfrac{1}{\text{rate}} = \dfrac{K_m + [S]}{V_{max}[S]}\]
or
\[ \dfrac{1}{\text{rate}} = \dfrac{K_m}{V_{max}} \dfrac{1}{[S]} + \dfrac{1}{V_{max}}\]
So a plot of \(1/rate\) as a function of \(1/[S]\) results in a straight line, the slope of which is equal to \(K_M/V_{max}\) and the intercept is \(1/V_{max}\). This is called a Lineweaver–Burk plot.

An example of a Lineweaver-Burk plot. (CC BY-SA 3.0; Diberri).


