2.3: Soluciones Oscilatorias a Ecuaciones Diferenciales

Objetivos de aprendizaje

• Explorar la base de las soluciones oscilatorias a la ecuación de onda
• Comprender las consecuencias de las condiciones de contorno sobre las posibles soluciones
• Racionalizar cómo las condiciones de límite satisfactorias fuerzan la cuantificación (es decir, solo existen soluciones con longitudes de onda específicas)

Las condiciones de contorno para la cadena mantenida en cero en ambos extremos argumentan que\(u(x,t)\) colapsa a cero en los extremos de la cadena (Figura 2.3.1 ).

Figura 2.3.1 : Ondas estacionarias en una cadena (tanto espacial como temporalmente). de Wikipedia.

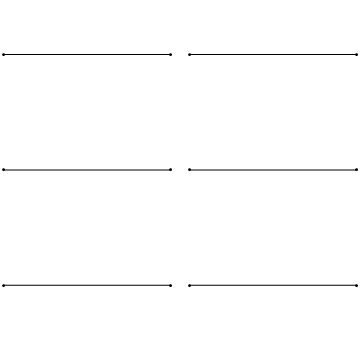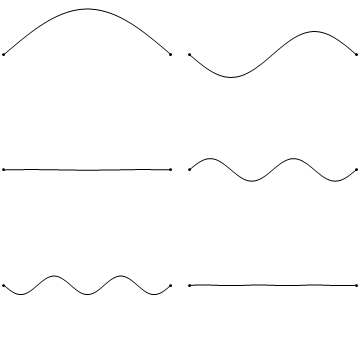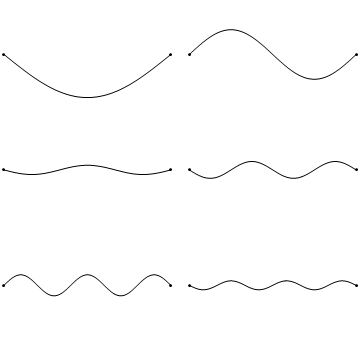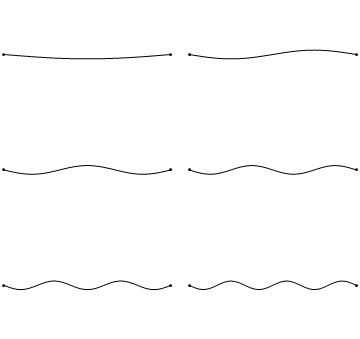
Desafortunadamente, cuando\(K>0\), la solución general (Ecuación 2.2.7) da como resultado una suma de decaimientos y crecimientos exponenciales que no pueden alcanzar las condiciones límite (a excepción de la solución trivial); de ahí\(K<0\). Esto significa que debemos introducir números complejos debido a los\(\sqrt{K}\) términos de la Ecuación 2.2.5. Así podemos reescribir\(K\):

\[K = - p^2 \label{2.3.1} \]

y la Ecuación 2.2.4b puede ser

\[\dfrac{d^2X(x)}{dx^2} +p^2 X(x) = 0 \label{2.3.2} \]

La solución general a las ecuaciones diferenciales de la forma de Ecuación\ ref {2.3.2} es

\[X(x) = A e^{ipx} + B e^{-ipx} \label{2.3.3} \]

Ejemplo 2.3.1

Verificar que Ecuación\(\ref{2.3.3}\) es la forma general para las ecuaciones diferenciales de la forma de Ecuación\(\ref{2.3.2}\), que cuando se sustituye con Ecuación\(\ref{2.3.1}\) dan

\[X(x) = A e^{ipx} + B e^{-ipx} \nonumber \]

Solución

Expandir los exponenciales complejos en funciones trigonométricas a través de la fórmula de Euler (\(e^{i \theta} = \cos \theta + i\sin \theta\))

\[X(x) = A \left[\cos (px) + i \sin (px) \right] + B \left[ \cos (px) - i \sin (px) \right] \nonumber \]

coleccionar términos similares

\[X(x) = (A + B ) \cos (px) + i (A - B) \sin (px) \label{2.3.6} \]

Introducir nuevas constantes complejas\(c_1=A+B\) y\(c_2=i(A-B)\) para que la solución general en Ecuación\(\ref{2.3.6}\) pueda expresarse como funciones oscilatorias

\[X(x) = c_1 \cos (px) + c_2 \sin (px) \label{2.3.7} \]

Ahora vamos a aplicar las condiciones de contorno de la Ecuación 2.2.7 para determinar las constantes\(c_1\) y\(c_2\). Sustituir la primera condición límite (\(X(x=0)=0\)) en las soluciones generales de Ecuación\(\ref{2.3.7}\) da como resultado

\[ \begin{align} X(x=0) = c_1 \cos (0) + c_2 \sin (0) &=0 \nonumber \\[4pt] c_1 + 0 &= 0 \nonumber \\[4pt] c_1 &=0 \label{2.3.8c} \end{align} \]

y sustituir la segunda condición límite (\(X(x=L)=0\)) en las soluciones generales de Ecuación\(\ref{2.3.7}\) da como resultado

\[ X(x=L) = c_1 \cos (pL) + c_2 \sin (pL) = 0 \label{2.3.9} \]

ya sabemos que\(c_1=0\) a partir de la primera condición límite así que Ecuación\(\ref{2.3.9}\) simplifica a

\[ c_2 \sin (pL) = 0 \label{2.3.10} \]

Dadas las propiedades de los senos, Ecuación\(\ref{2.3.9}\) simplifica a

\[ pL= n\pi \label{2.3.11} \]

con\(n=0\) es la solución trivial que así ignoramos\(n = 1, 2, 3...\).

\[ p = \dfrac{n\pi}{L} \label{2.3.12} \]

La sustitución de ecuaciones\(\ref{2.3.12}\) y\(\ref{2.3.8c}\) en la ecuación\(\ref{2.3.7}\) da como resultado

\[X(x) = c_2 \sin \left(\dfrac{n\pi x}{L} \right) \nonumber \]

que puede simplificar a

\[X(x) = c_2 \sin \left( \omega x \right) \nonumber \]

con

\[\omega=\dfrac{n\pi}{L} \nonumber \]

Un argumento similar se aplica a la otra mitad del ansatz (\(T(t)\)).

Ejercicio 2.3.1

Dadas dos olas viajeras:\[ \psi_1 = \sin{(c_1 x+c_2 t)} \; \textrm{ and } \; \psi_2 = \sin{(c_1 x-c_2 t)} \nonumber \]

1. Encuentra la longitud de onda y la velocidad de onda de\( \psi_1 \) y\( \psi_2 \)
2. Encuentre los siguientes nodos e identifique:\[ \psi_+ = \psi_1 + \psi_2 \; \textrm{ and } \; \psi_- = \psi_1 - \psi_2 \nonumber \]

Solución a:

\(\psi_1 \)es una función de pecado. En cada entero\( n \pi \) donde\(n=0,\pm 1, \pm 2, ... \), una función sin será cero. Así,\( \psi_1 = 0 \) cuando\(c_1 x + c_2 t = \pi n \). Resolviendo para la x, ignorando soluciones triviales:

\[ x = \frac{n \pi - c_2 t}{c_1} \nonumber \]

La velocidad de esta ola es:

\[ \frac{dx}{dt} = -\frac{c_2}{c_1} \nonumber \]

De manera similar para\( \psi_2 \). En cada entero\( n \pi \) donde\(n=0,\pm 1, \pm 2, ... \), una función sin será cero. Así,\( \psi_2 = 0 \) cuando\(c_1 x - c_2 t = \pi n \). Resolviendo para x, para\( \psi_2 \):

\[ x = \frac{n \pi + c_2 t}{c_1} \nonumber \]

La velocidad de esta ola es:

\[ \frac{dx}{dt} = \frac{c_2}{c_1} \nonumber \]

La longitud de onda para cada onda es el doble de la distancia entre dos nodos sucesivos. En otras palabras,

\[ \lambda = 2(x_{n} - x_{n-1}) = \frac{2 \pi}{c_1} \nonumber \]

Solución b:

Encuentra\( \psi_+ = \psi_1 + \psi_2 \; \textrm{ and } \; \psi_- = \psi_1 - \psi_2 \).

\[ \begin{align*} \psi_+ &= \sin (c_1 x + c_2 t) + \sin (c_1 x - c_2 t) \\[4pt] &= \sin (c_1 x ) \cos (c_2 t) + \cancel{\cos(c_1 x) \sin(c_1 t)} + \sin (c_1 x ) \cos (c_2 t) - \cancel{\cos(c_1 x) \sin(c_1 t)} \\[4pt] &= 2\sin (c_1 x ) \cos (c_2 t) \end{align*} \nonumber \]

Esto debería tener un nodo en cada\( x= n \pi / c_1 \) y

\[ \begin{align*} \psi_- &= \sin (c_1 x + c_2 t) - \sin (c_1 x - c_2 t) \\[4pt] &= \cancel{\sin (c_1 x ) \cos (c_2 t)} + \cos(c_1 x) \sin(c_1 t) - \cancel{\sin (c_1 x ) \cos (c_2 t)} + \cos(c_1 x) \sin(c_1 t) \\[4pt] &= 2\cos (c_1 x ) \sin (c_2 t) \end{align*} \nonumber \]