2.4: La solución general es una superposición de modos normales
- Page ID
- 80170
- Separar la ecuación de onda en problemas espaciales y temporales individuales y resolverlos.
- Demostrar que la solución general puede ser una superposición de soluciones (modos normales)
Como se discutió anteriormente, las soluciones a la cadena de ejemplo\(u(x,t)\) para todos\(x\) y se\(t\) asumirían como producto de dos funciones:\(X(x)\) y\(T(t)\), donde\(X(x)\) es una función de solo\(x\), no\(t\) y\(T(t)\) es una función de\(t\), pero no \(x\).
\[u(x,t)= X(x)T(t) \nonumber \]
Al sustituir la nueva forma de solución de producto en la ecuación de onda original, se pueden obtener dos ecuaciones diferenciales ordinarias (ecuación diferencial que contiene una función o funciones de una variable independiente y sus derivadas). Cada ecuación diferencial implicaría solo una de las variables independientes (\(x\)o\(t\)).
Dependencia Espacial de la Solución:\(X(x)\)
Las condiciones de contorno para la cadena mantenida en cero en ambos extremos argumentan que\(u(x,t)\) se colapsa a cero en los extremos de la cadena. Desafortunadamente, cuando\(K>0\), la solución general a la ecuación de onda da como resultado una suma de decaimientos y crecimientos exponenciales que no pueden alcanzar las condiciones límite (a excepción de la solución trivial que\(u(x,t)=0\)); de ahí\(K<0\). Esto significa que debemos introducir números complejos debido a los\(\sqrt{K}\) términos de la Ecuación 2.2.5. Para que podamos reescribir\(K\):
\[K = - p^2 \label{2.4.1} \]
y la Ecuación 2.2.4b puede ser
\[\dfrac{d^2X(x)}{dx^2} +p^2 X(x) = 0 \label{2.4.2} \]
La solución general a las ecuaciones diferenciales de la forma de Ecuación\(\ref{2.4.2}\) es la Ecuación 2.2.5
\[X(x) = A e^{\sqrt{K}x} + B e^{-\sqrt{K}x} \label{2.4.3} \]
que cuando se sustituye con Ecuación\(\ref{2.4.1}\) dar
\[X(x) = A e^{ipx} + B e^{-ipx} \label{2.4.4} \]
Los exponenciales complejos se pueden expresar como funciones trigonométricas a través de la fórmula de Euler (\(e^{i \theta} = \cos \theta + i\sin \theta\))
\[X(x) = A \left[\cos (px) + i \sin (px) \right] + B \left[ \cos (px) - i \sin (px) \right] \nonumber \]
coleccionar términos similares
\[X(x) = (A + B ) \cos (px) + i (A - B) \sin (px) \label{2.4.6} \]
Introducir nuevas constantes complejas\(C=A+B\) y\(D=i(A-B)\) para que la solución general en Ecuación\(\ref{2.4.6}\) pueda expresarse como funciones oscilatorias
\[X(x) =C \cos (px) + D \sin (px) \label{2.4.7} \]
Verificar que la Ecuación\ ref {2.4.3} es la forma general para las ecuaciones diferenciales de la forma de Ecuación\(\ref{2.4.2}\).
- Contestar
-
Con el fin de demostrar que
\[X(x)=A e^{\sqrt{x} x}+B e^{-\sqrt{x} x} \label{2.2.4} \]
es una solución general a la ecuación diferencial
\[\frac{d^{2} X(x)}{d x^{2}}+p^{2} X(x)=0. \nonumber \]
Luego tenemos que tomar la segunda derivada de la Ecuación\ ref {2.2.4} y sustituirla y la función original en las ubicaciones apropiadas en la Ecuación\ ref {2.4.3} y verificar que de hecho sea igual\(0\).
Primero tenemos que tomar la primera y luego la segunda derivada de la Ecuación\ ref {2.2.4}
\ [\ begin {array} {l}
{\ dfrac {d} {d x}\ izquierda (A e^ {\ sqrt {k x}} +B e^ {-\ sqrt {k} x}\ derecha) =\ sqrt {k} A e^ {\ sqrt {k x}} -\ sqrt {k} B e^ {-\ sqrt {k x}}\\
{\ dfrac {d^ {2}} {d x^ {2}}\ izquierda (A e^ {\ sqrt {k x}} +B e^ {-\ sqrt {k} x}\ derecha) =k A e^ {\ sqrt {k x}} +k B e^ {-\ sqrt {k x}}}
\ end { matriz}\ nonumber\]Ahora que tenemos la segunda derivada de la Ecuación\ ref {2.2.4} conectamos los valores relevantes en la Ecuación\ ref {2.4.2}
\[\begin{align*} \dfrac{d^{2} X(x)}{d x^{2}}+p^{2} X(x)=0 \\ k A e^{\sqrt{k} x}+k B e^{-\sqrt{k} x}+p^{2}\left(A e^{\sqrt{k} x}+B e^{-\sqrt{k} x}\right) \overset{?}{=} 0 \end{align*} \nonumber \]
Se nos da en la Ecuación\ ref {2.4.2} que
\[ k=-p^{2} \nonumber \]
Entonces
\[p^{2}=-k \nonumber \]
Ahora podemos enchufar eso en nuestra ecuación diferencial para simplificar
\[\begin{align*} k A e^{\sqrt{k} x}+k B e^{-\sqrt{k} x} - k\left(A e^{\sqrt{k} x}+B e^{-\sqrt{k} x} \right) &\overset{?}{=} 0 \\[4pt] \bcancel{ k A e^{\sqrt{k x}}} + \cancel{k B e^{-\sqrt{k x}}} - \bcancel{k A e^{\sqrt{k x}}} - \cancel{k B e^{-\sqrt{k x}}} & \overset{\checkmark}{=} 0 \end{align*} \nonumber \]
Como todos estos términos cancelan a igual 0, demostramos que la solución dada es una solución general a la ecuación diferencial. Sin embargo, es importante recordar que no es la única solución a la ecuación diferencial.
Ahora vamos a aplicar las condiciones de contorno de la Ecuación 2.2.7 para determinar las constantes\(C\) y\(D\). Sustituir la primera condición límite (\(X(x=0)=0\)) en las soluciones generales de Ecuación\(\ref{2.4.7}\) da como resultado
\[\begin{align} X(x=0) &= 0 \\[4pt] C \cos (0) + D \sin (0) &=0 \label{2.4.8a} \\[4pt] C + 0 &= 0 \label{2.4.8b} \\[4pt] C&=0 \label{2.4.8c} \end{align} \]
y sustituir la segunda condición límite (\(X(x=L)=0\)) en las soluciones generales de Ecuación\(\ref{2.4.7}\) da como resultado
\[ X(x=L) = C \cos (pL) + D \sin (pL) = 0 \label{2.4.9} \]
ya sabemos que\(C=0\) a partir de la primera condición límite así Ecuación\(\ref{2.4.9}\) simplifica a
\[ D \sin (pL) = 0 \label{2.4.10} \]
Dadas las propiedades de los senos, Ecuaciones\ ref {2.4.9} simplifica a
\[ pL= n\pi \label{2.4.11} \]
con\(n=0\) es la solución trivial que así ignoramos\(n = 1, 2, 3...\).
\[ p = \dfrac{n\pi}{L} \label{2.4.12} \]
La sustitución de ecuaciones\(\ref{2.4.12}\) y\(\ref{2.4.8c}\) en la ecuación\(\ref{2.4.7}\) da como resultado
\[X(x) = D \sin \left(\dfrac{n\pi x}{L} \right) \label{2.4.13} \]
Ecuación\(\ref{2.4.13}\) presenta un conjunto de soluciones a la parte espacial de la solución a la ecuación de onda sujeta a las condiciones de contorno (Figura 2.4.1 ). Este conjunto de soluciones es infinitamente grande con soluciones individuales que se distinguen entre sí por el\(n\) parámetro introducido para dar cuenta de las condiciones de contorno. Este número es un ejemplo de un “número cuántico” que están ubicuamente en la mecánica cuántica y están definidos de manera única para cada sistema.
Dependencia del Tiempo de la Solución:\(T(t)\)
Un argumento similar se aplica a la otra mitad del ansatz (\(T(t)\)) originalmente propuesto para la ecuación de onda clásica que se obtuvo al resolver la Ecuación 2.2.4a, que cualitativamente se asemeja a la ecuación diferencial espacial original resuelta anteriormente (Ecuación 2.2.4b).
\[ \dfrac{d^2T(t)}{dt^2} - Kv^2 T(t) = 0 \nonumber \]
Sin embargo, las restricciones extraídas de la resolución de la dependencia espacial se aplican a la dependencia del tiempo. Cuando las Ecuaciones\(\ref{2.4.1}\) y\(\ref{2.4.12}\) se sustituyen en la Ecuación 2.2.4a, se obtiene una expresión más simplificada
\[ \dfrac{d^2T(t)}{dt^2} + p^2v^2 T(t) = \dfrac{d^2T(t)}{dt^2} + \left(\dfrac{n v \pi}{L}\right)^2 T(t) = 0 \label{2.4.14} \]
Definir una nueva constante:\(\omega_n\)
\[\omega_n= \left(\dfrac{n v \pi}{L}\right) \label{2.4.15} \]
y sustituirlo en Ecuación\(\ref{2.4.14}\)
\[ \dfrac{d^2T(t)}{dt^2} + \omega_n^2 T(t) = 0 \label{2.4.16} \]
Esta es la misma forma funcional de la Ecuación\(\ref{2.4.2}\)
\[ T(t) = E \cos (\omega_n t) + F \sin (\omega_n t) \label{2.4.17} \]
En contraste con la solución de dependencia espacial, no tenemos condiciones de límite para usar para identificar las constantes\(E\) y\(F\).
El principio de superposición
Ahora volvamos a revisar la solución original de ansatz a la ecuación de onda clásica (Ecuación 2.2.1), que puede sustituirse con Ecuaciones\(\ref{2.4.13}\) y\(\ref{2.4.17}\)
\[\begin{align} u(x,t) &= X(x)T(t) \label{2.4.19a}\ \\[4pt] &= \left[D \sin \left(\dfrac{n\pi x}{L} \right) \right] \left( E \cos (\omega_n t) + F \sin (\omega_n t) \right) \end{align} \label{2.4.18b} \]
podemos recoger constantes nuevamente con\(G=DE\) y\(H=DF\) e introducir una\(n\) dependencia a cada uno desde entonces\(E\) y\(F\) puede ser\(n\) dependencia.
\[u_n(x,t) = \left[ G_n \cos (\omega_n t) + H_n \sin (\omega_n t) \right] \sin \left(\dfrac{n\pi x}{L} \right) \label{2.4.19} \]
Las funciones representadas en Ecuación\(\ref{2.4.19}\) son un conjunto de soluciones que incluyen características espaciales y temporales que resuelven la ecuación de onda de una cuerda apretada en dos extremos.
La ecuación de onda tiene una propiedad muy importante: si tenemos dos soluciones a la ecuación, entonces la suma de las dos es también una solución a la ecuación. Es fácil verificar esto:
\[ \dfrac{\partial^2 (f+g)}{\partial x^2} = \dfrac{\partial^2 f}{\partial x^2} + \dfrac{\partial^2 g}{\partial x^2} = \dfrac{1}{v^2} \dfrac{\partial^2f}{\partial t^2} +\dfrac{1}{v^2} \dfrac{\partial^2g}{\partial t^2} = \dfrac{1}{v^2} \dfrac{\partial^2(f+g)}{\partial t^2} \nonumber \]
Cualquier ecuación diferencial para la que se mantenga esta propiedad se denomina ecuación diferencial lineal. También tenga en cuenta que también\(af(x,t) + bg(x,t)\) es una solución a la ecuación si\(a\),\(b\) son constantes. Así puedes sumar, superponer, múltiplos de dos soluciones cualesquiera de la ecuación de onda para encontrar una nueva función que satisfaga la ecuación.
Esta importante propiedad es fácil de interpretar visualmente: si puedes dibujar dos soluciones de onda, entonces en cada punto de la cuerda simplemente agrega el desplazamiento\(u_n(x,t)\) de una onda a la otra\(u_m(x,t)\) —la suma de las dos ondas juntas es una solución. Entonces, por ejemplo, a medida que dos ondas viajeras que se mueven a lo largo de la cuerda en direcciones opuestas se encuentran entre sí, el desplazamiento de la cuerda en cualquier punto en cualquier instante es solo la suma de los desplazamientos que habría tenido de las dos olas individualmente.
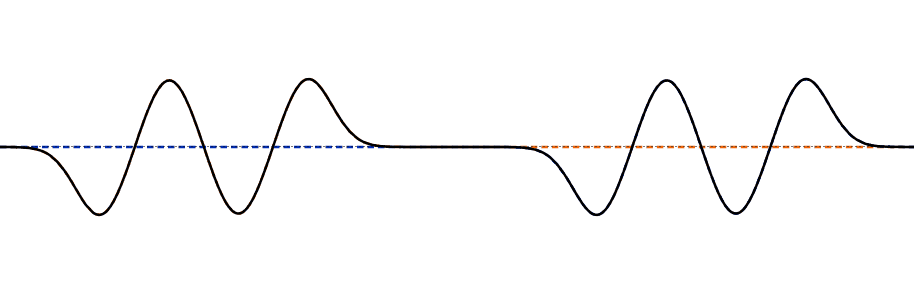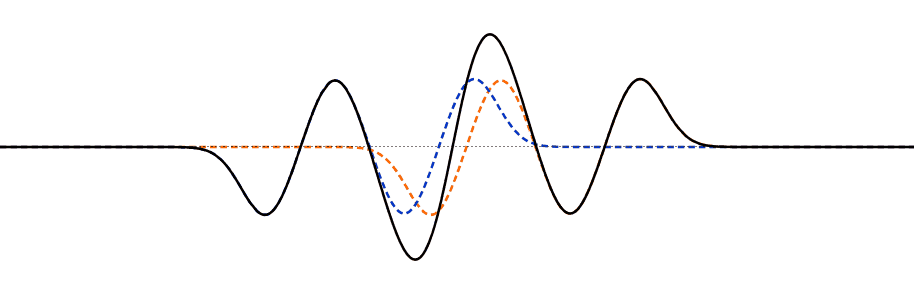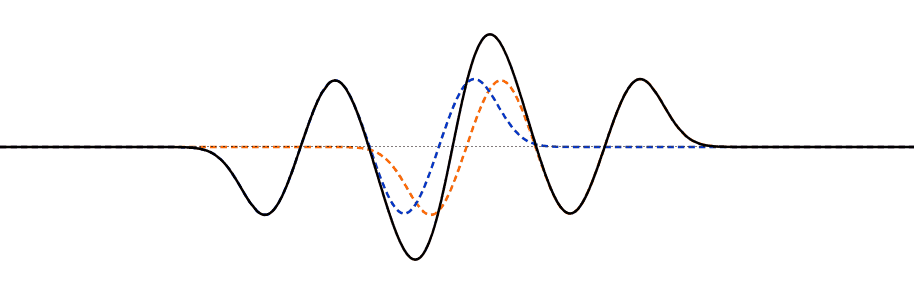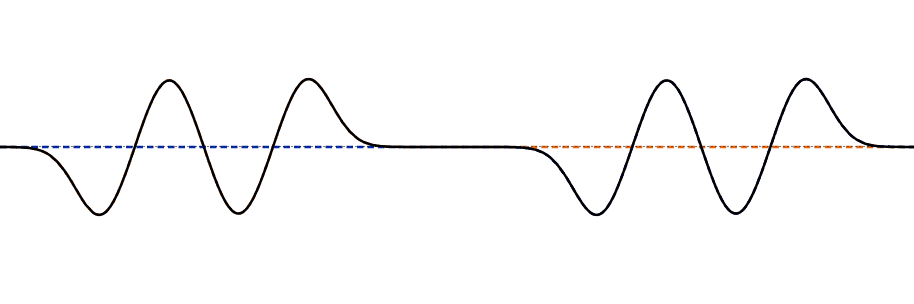
Esta simple adición de los desplazamientos es interferencia, sin duda porque si las olas que se encuentran tienen desplazamientos en direcciones opuestas, la cuerda se desplazará menos que en una sola onda. Esto también se llama el Principio de Superposición.
El Principio de Superposición es la suma de dos o más soluciones también es una solución.
Dado que la ecuación de onda es una ecuación diferencial homogénea lineal, la solución total se puede expresar como una suma de todas las soluciones posibles descritas por la ecuación\(\ref{2.4.19}\).
\[\begin{align} u(x,t) &= \sum_{n=1}^{\infty} u_n(x,t) \label{2.4.20} \\[4pt] & = \sum_{n=1}^{\infty} \left( G_n \cos (\omega_n t) + H_n \sin (\omega_n t) \right) \sin \left(\dfrac{n\pi x}{L}\right) \label{2.4.21} \end{align} \]
Cada\(u_n(x,t)\) solución se llama un modo normal del sistema y se puede caracterizar a través de sus frecuencias correspondientes\(\dfrac{n\pi}{L}\) con\(n=1,2,3...\). La dependencia espacial de los primeros siete modos normales se muestra en la Figura 2.4.1 y son ondas estacionarias. El primer término con\(n=1\) se llama típicamente el fundamental y cada modo subsiguiente se llama armónico o armónico. La dependencia temporal de los modos normales es sinusoidal con frecuencias angulares\(\omega_n\) que pueden expandirse a frecuencias naturales\(\nu_n\) vía
\[ \nu_n = \dfrac{\omega_n}{2 \pi} = \dfrac{nv}{2L} \label{2.4.22} \]
De ahí que a medida que aumenta la curvatura espacial del modo normal, la oscilación temporal de ese modo también aumenta. Este es un rasgo común en los sistemas mecánicos cuánticos y es una consecuencia directa de la ecuación de onda.

