2.5: Una membrana vibratoria
- Page ID
- 80168
- Aplicar las ecuaciones de onda a una membrana bidimensional (rectángulos y círculos)
- Reconocer las posibles geometrías de un nodo en sistemas bidimensionales
Hasta ahora, hemos mirado olas en una dimensión, viajando a lo largo de una cuerda o ondas sonoras bajando por un tubo estrecho. Sin embargo, las olas en dimensiones más altas que una son muy familiares: olas de agua en la superficie de un estanque o ondas sonoras que salen de una fuente en tres dimensiones. Es agradable encontrar que estas ondas en dimensiones superiores satisfacen ecuaciones de onda que son una extensión muy natural de la que encontramos para una cuerda, y —muy importante— también satisfacen el Principio de Superposición, es decir, si las olas se encuentran, solo agregas la contribución de cada ola. En los dos párrafos siguientes, entramos en más detalle, pero este Principio de Superposición es la lección crucial.
La ecuación de onda y superposición en más dimensiones
¿Qué sucede en dimensiones superiores? Consideremos dos dimensiones, por ejemplo ondas en una sábana elástica como una parilla de tambor. Si la posición de reposo para la lámina elástica es el plano (\(x\),\(y\)), por lo que cuando está vibrando se mueve hacia arriba y hacia abajo en la dirección z, su configuración en cualquier instante del tiempo es una función. \(u(x,y,t)\)
De hecho, podríamos hacer lo mismo que hicimos por la cuerda, mirando las fuerzas totales en un poquito y aplicando la Segunda Ley de Newton. En este caso eso significaría tomar un poco del parche del tambor, y en lugar de un pequeño tramo de cuerda con tensión tirando de los dos extremos, tendríamos un pequeño cuadrado de la lámina elástica, con tensión tirando por todo el borde. Recuerden que la fuerza neta sobre el trozo de cuerda se produjo porque la cuerda se estaba curvando alrededor, por lo que las tensiones en los extremos opuestos tiraron en direcciones ligeramente diferentes, y no cancelaron. El\(\frac{\partial^2}{\partial x^2}\) término midió esa curvatura, la tasa de cambio de pendiente. En dos dimensiones, pensando en un pequeño cuadrado de la lámina elástica, las cosas se complican más. Visualiza el trozo de hoja para que sea momentáneamente como un pequeño parche en un globo, verás que se curva en dos direcciones, y las fuerzas de tensión deben estar tirando alrededor de los bordes. La fuerza total sobre el pequeño cuadrado se produce porque las fuerzas de tensión en lados opuestos están fuera de línea si la superficie se curva alrededor, ahora tenemos que sumar dos conjuntos de fuerzas casi opuestas de los dos pares de lados. La matemática ahora se muestra aquí, pero es al menos plausible que la ecuación sea:
\[ \dfrac{ \partial^2 u(x,y,t)}{\partial x^2} + \dfrac{ \partial^2 u(x,y,t)}{\partial y^2} = \dfrac{1}{v^2} \dfrac{ \partial^2 u(x,y,t)}{\partial t^2} \label{2.5.1} \]
La física de esta ecuación es que la aceleración de un poquito de la hoja proviene de tensiones de desequilibrio provocadas por la curva de la hoja tanto en la dirección x - como en y, es por ello que están los dos términos en el lado izquierdo.
Y, ir a tres dimensiones es fácil: agregar un término más para dar
\[ \dfrac{ \partial^2 u(x,y,,z,t)}{\partial x^2} + \dfrac{ \partial^2 u(x,y,z,t)}{\partial y^2} + \dfrac{ \partial^2 u(x,y,z,t)}{\partial z^2} = \dfrac{1}{v^2} \dfrac{ \partial^2 u(x,y,z,t)}{\partial t^2} \label{2.5.2} \]
Esta suma de diferenciaciones parciales en el espacio es tan común en la física que hay una taquigrafía:
\[ \nabla^2 = \left( \dfrac{ \partial^2}{\partial x^2}, \dfrac{ \partial^2}{\partial y^2}, \dfrac{ \partial^2}{\partial z^2} \right) \label{2.5.4} \]
así que la ecuación\ ref {2.5.2} se puede escribir más fácilmente como
\[ \nabla^2 u(x,y,z,t) = \dfrac{1}{v^2} \dfrac{\partial^2 u(x,y,z,t)}{\partial t^2} \label{2.5.3} \]
Así como encontramos en una dimensión ondas armónicas viajeras (sin condiciones de límite)
\[u(x,t) = A \sin (kx -\omega t) \label{2.5.5} \]
con\(\omega=\nu k \), se puede verificar que la ecuación tridimensional tiene soluciones armónicas
\[u(x,y,z,t) = A \sin (k_x x +k_x +k_z z -\omega t) \label{2.5.6} \]
con\(\omega = \nu |\vec{k|}\) donde\(|k| = \sqrt{k_x^2+k_y^2+k_z^2}\)
\(\vec{k}\)es un vector en la dirección en la que se mueve la onda. Los campos eléctricos y magnéticos en una onda de radio u onda de luz tienen justamente esta forma (o, más cerca de la fuente, una expresión equivalente muy similar para las esferas salientes de ondas, en lugar de las ondas planas).
Es importante darse cuenta de que la ecuación de onda 2D (Ecuación\ ref {2.5.1}) sigue siendo una ecuación lineal, por lo que el Principio de Superposición aún se mantiene. Si dos olas sobre una lámina elástica, o la superficie de un estanque, se encuentran entre sí, el resultado en cualquier punto se da simplemente agregando los desplazamientos de las olas individuales. Comenzaremos pensando en las olas que se propagan libremente en dos y tres dimensiones, que más tarde consideraremos las olas en áreas restringidas, como una cabeza de tambor.
Modos vibracionales de una membrana rectangular
Una onda unidimensional no tiene opción en cómo se propaga: simplemente se mueve a lo largo de la línea (bueno, podría reflejarse en parte por algún cambio en la línea y parte de ella ir hacia atrás). Sin embargo, cuando vamos a dimensiones más altas, la forma en que se extiende una perturbación de las olas que comienza en alguna región localizada está lejos de ser obvia. Pero podemos comenzar recordando algunos casos simples: dejar caer un guijarro en agua sin gas provoca un círculo de ondas que se mueve hacia afuera. Si concedemos que la luz es una onda, notamos que un haz de luz cambia de dirección al pasar del aire al vidrio. Por supuesto, no es inmediatamente evidente que la luz es una ola: hablaremos mucho más de eso más adelante. A continuación se muestran algunas soluciones (tanto temporales como espaciales) junto con sus números cuánticos (\(n_x\)y\(n_y\)).
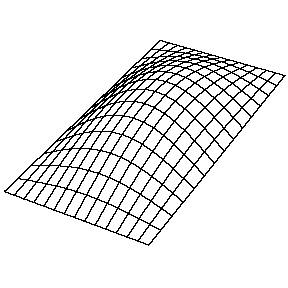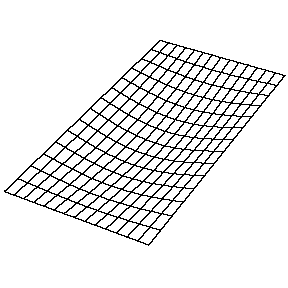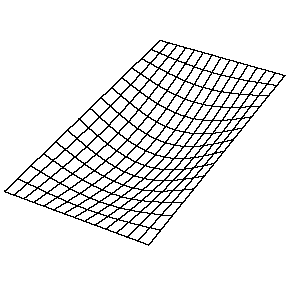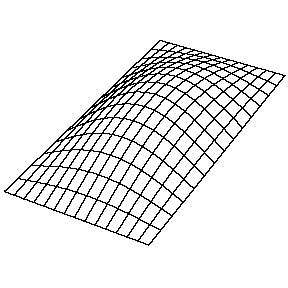
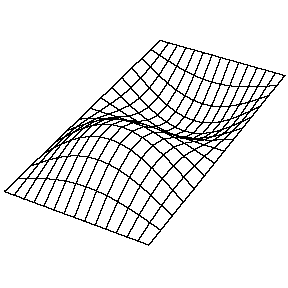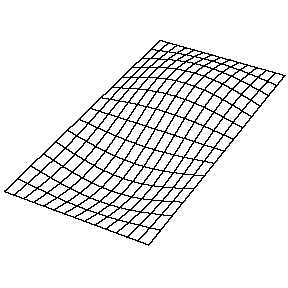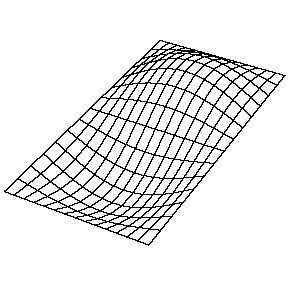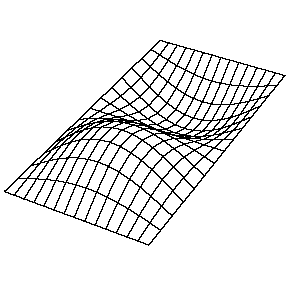
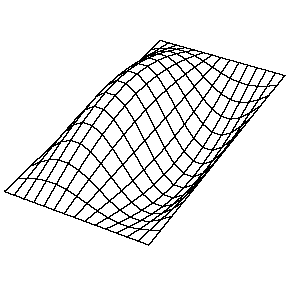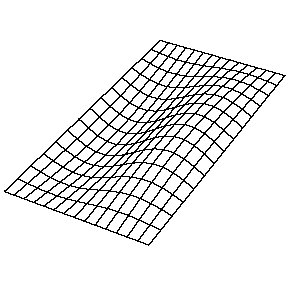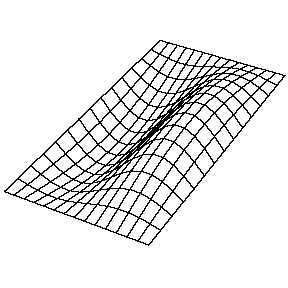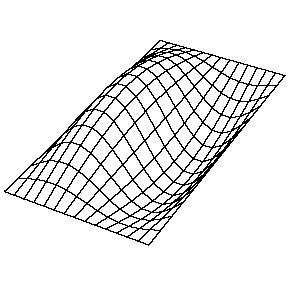

La resolución de la función\(u(x,y,t)\) en una membrana vibrante y rectangular se realiza de manera similar mediante la separación de variables y el establecimiento de condiciones de límite. La función resuelta es muy similar, donde
\[u(x,y,t) = A_{nm} \cos(\omega_{nm} t + \phi_{nm}) \sin \left(\dfrac {n_x \pi x}{a}\right) \sin\left(\dfrac {n_y\pi y}{b}\right) \label{2.5.6b} \]
donde
- \(a\)es la longitud de la membrana rectangular y\(b\) es la anchura, y
- \(n_x\)y\(n_y\) son dos números cuánticos (uno en cada dimensión).
Al igual que con las soluciones a las ecuaciones de onda 1-D, un nodo es un punto (o línea) en una estructura que no se mueve mientras el resto de la estructura está vibrando.
Para las siguientes soluciones 2-D en la Figura 2.5.1 , ¿cuántos nodos hay, cuál es la geometría y cómo los caracterizarías?
- (\(n_x=1\),\(n_y=1\)
- (\(n_x=2\),\(n_y=1\)
Solución
a. La\(n_y=1\) solución (\(n_x=1\), en la Figura 2.5.1 tiene cero nodos. Es decir, ningún punto en la membrana (que no sea los límites) no se mueve durante el movimiento de la membrana.
b. La\(n_y=1\) solución (\(n_x=2\), en la Figura 2.5.1 tiene un nodo. Es una línea a la mitad de la longitud de la dirección x y se extiende sobre toda la longitud de la dirección y.
Para la (\(n_x=2\),\(n_y=2\) solución a una membrana rectangular en la Figura 2.5.1 : ¿cuántos nodos hay, cuál es la geometría y cómo los caracterizarías?
- Responder
-
Hay dos nodos. Son líneas y una está a la mitad de la longitud de la dirección x y se extiende sobre toda la longitud de la dirección y y una si y una está a la mitad de la longitud de la dirección y y se extiende sobre toda la longitud de la dirección x
Modos vibracionales de una membrana circular
Los principios básicos de una membrana rectangular vibrante se aplican a otros miembros 2-D incluyendo membranas circulares. Sin embargo, las matemáticas y las soluciones son un poco más complicadas. Las soluciones se representan mejor en notación polar (en lugar de rectangular como en la Ecuación\ ref {2.5.6b}) y tienen la siguiente forma funcional
\[u(r, \theta, t)=J_{m}\left(\lambda_{m n} r\right) \cos m \theta \cos c \lambda_{m n} t \nonumber \]
donde\(J_m\) están las funciones de Bessel (estas son funciones oscilatorias) y\(\lambda\) son constantes. Este sistema tiene dos números cuánticos (\(m\)y\(n\)) que cumplen la misma función que\(n_x\) y\(n_y\) hacen en las membranas rectangulares. En las animaciones de la Figura 2.5.2 , los diámetros nodales y los círculos aparecen como regiones blancas que no oscilan, mientras que las regiones roja y azul indican desplazamientos positivos y negativos.
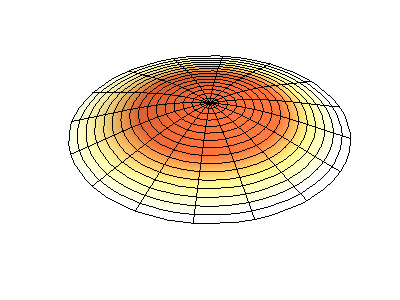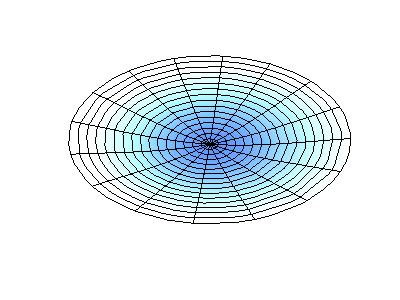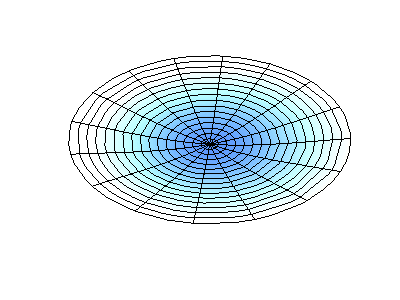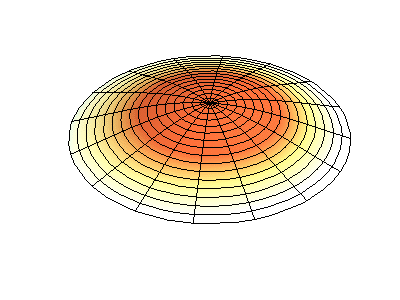
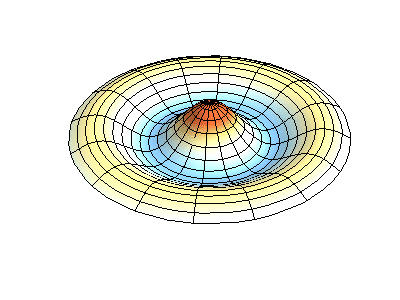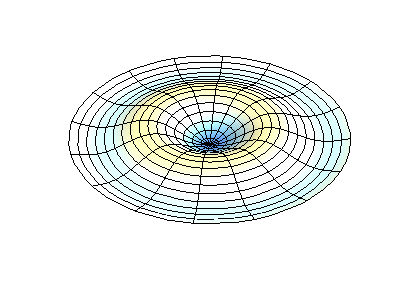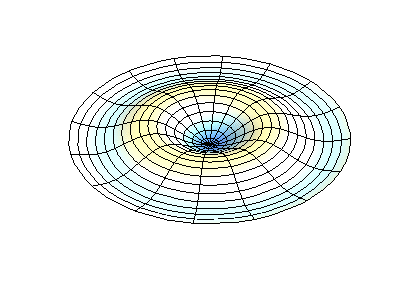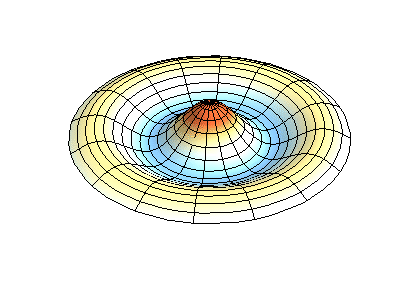
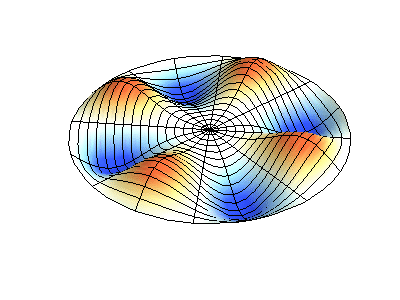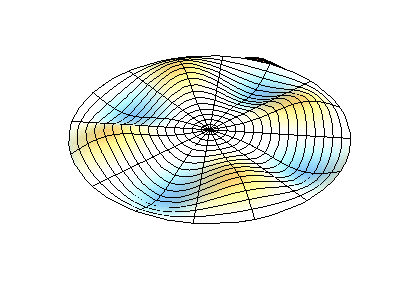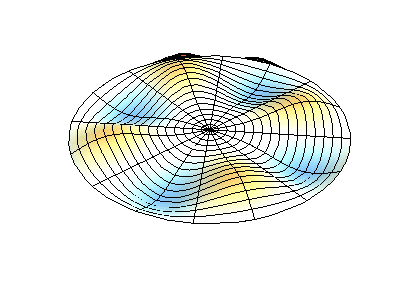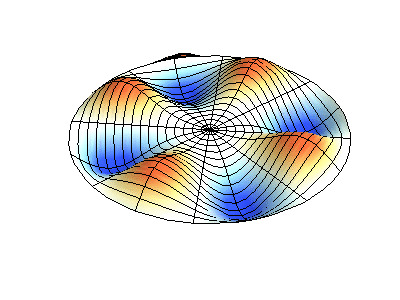
La figura 2.5.2 (izquierda) muestra la forma de modo fundamental para una membrana circular vibrante, mientras que los otros dos modos son modos excitados con carácter nodal más complejo.
¿Cuántos nodos hay en las tres soluciones para una membrana circular en la Figura 2.5.2 , cuáles son sus geometrías, y cómo los caracterizarías?
- Responder
-
(izquierda) cero nodos
(medio) dos nodos. Son circulares en aproximadamente 1/3 y 2/3 del radio (estos son nodos radiales = en radios fijos)
(derecha) cuatro nodos. Son líneas en ángulo de 45° desde el centro (estos son nodos angulares = en ángulos fijos).
Colaborador
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)
- Delmar Larsen

