3.E: La ecuación de Schrödinger y una partícula en una caja (Ejercicios)

Las soluciones para seleccionar preguntas se pueden encontrar en línea.

3.2

Determine a partir de los siguientes operadores que son lineales y no lineales:

1. \(\hat{A}f(x)= f(x)^2\)[cuadrado f (x)]
2. \(\hat{A}f(x)= f^*(x)\)[formar el complejo conjugado de f (x)]
3. \(\hat{A}f(x)= 0\)[multiplicar f (x) por cero]
4. \(\hat{A}f(x)= [f(x)]^{-1}\)[tomar el recíproco de f (x)]
5. \(\hat{A}f(x)= f(0)\)[evaluar f (x) a x=0]
6. \(\hat{A}f(x)= \ln f(x)\)[tomar el registro de f (x)]

Solución

Es importante tener en cuenta que un operador\(\hat{A}\) es lineal si

\[ \underbrace{\hat{A}[c_1f(x)+c_2f_2(x)]}_{\text{left side}}= \underbrace{c_1\hat{A}f_1(x)+c_2\hat{A}f_2(x) }_{\text{right side}}\nonumber \]

y el operador no es lineal si

\[ \underbrace{ \hat{A}[c_1f_1(x)+c_2f_2(x)]}_{\text{left side}} \neq \underbrace{ c_1\hat{A}f_1(x)+c_2\hat{A}f_2(x) }_{\text{right side}}\nonumber \]

a)

Evaluar el lado izquierdo

\[\begin{align*} \hat{A}[c_1f(x)+c_2f_2(x)] &= [c_1f_1(x)+c_2f_2(x)]^2 \\ &= c_1^2 f_1(x)^2+2c_1f_1(x) c_2f_2(x)+c_2^2f_2(x)^2 \end{align*}\nonumber \]

Evaluar el lado derecho

\[c_1 \hat{A} f_1(x)+c_2\hat{A}f_2(x)=c_1[f_1(x)]^2+c_2[f_2(x)]^2 \neq \hat{A}[c_1f_1(x)+c_2f_2(x)] \nonumber \]

Este operador no es lineal

b)

Evaluar el lado izquierdo

\[\hat{A}[c_1f_1(x)+c_2f_2(x)] = c_1^*f_1^*(x) + c_2^*f_2^*(x)\nonumber \]

Evaluar el lado derecho

\[\begin{align*} c_1\hat{A}f_1(x) + c_2\hat{A}f_2(x) &= c_1f_1^*(x) + c_2f_2^*(x) \\[4pt] &= \hat{A}[c_1f_1(x) + c_2f_2(x)] \end{align*} \]

Este operador es lineal

c)

Evaluar el lado izquierdo

\[ \hat{A}[c_1f_1(x)+c_2f_2(x)] = 0\nonumber \]

Evaluar el lado derecho

\[c_1\hat{A}f_1(x) + c_2\hat{A}f_2(x) = c_1f_1(x) + c_2f_2(x) = 0\nonumber \]

\[ = \hat{A}[c_1f_1(x) + c_2f_2(x)]\nonumber \]

Este operador es lineal

d)

Evaluar el lado izquierdo

\[\hat{A}[c_1f_1(x)+c_2f_2(x)] = \dfrac{1}{c_1f_1(x) + c_2f_2(x)}\nonumber \]

Evaluar el lado derecho

\[c_1\hat{A}f_1(x) + c_2\hat{A}f_2(x) = \dfrac{c_1}{f_1(x)} + \dfrac{c_2}{f_2(x)} \nonumber \]

\[ \neq \hat{A}[c_1f_1(x) + c_2f_2(x)]\nonumber \]

Este operador no es lineal

e)

Evaluar el lado izquierdo

\[\hat{A}[c_1f_1(x)+c_2f_2(x)] = c_1f_1(0) + c_2f_2(0)\nonumber \]

Evaluar el lado derecho

\[ = c_1\hat{A}f_1(x) + c_2\hat{A}f_2(x)\nonumber \]

Este operador es lineal

 

f)

Evaluar el lado izquierdo

\[\hat{A}[c_1f_1(x)+c_2f_2(x)] = \ln [c_1f_1(x) + c_2f_2(x)]\nonumber \]

Evaluar el lado derecho

\[c_1\hat{A}f_1(x) + c_2\hat{A}f_2(x) = c1 \ln f_1(x) + c_2 \ln f_2(x)\nonumber \]

\[ \neq \hat{A}[c_1f_1(x) + c_2f_2(x)]\nonumber \]

Este operador no es lineal

3.8

Mostrar que para una partícula en una caja con longitud a con estado\(n=3\) that there are 3 locations along the x axis where the probability density is at a maximum.

Solución

La densidad de probabilidad para una partícula en una caja para el estado\(n=3\) is

\[{\psi}^*{\psi}=\dfrac{2}{a}{\sin}^2\dfrac{3px}{a}\nonumber \]

Para maximizar la densidad de probabilidad, tomar su derivada y establecerla igual a cero y resolver para\(x\) .

\[\dfrac{d}{dx}\left[\dfrac{2}{a}{{\sin}^2 \dfrac{3{\pi}x}{a}\ }\right]=\dfrac{2}{a}\cdot 2\cdot {\sin \dfrac{3{\pi}x}{a}\ }\cdot {\cos \dfrac{3{\pi}x}{a}\ }\cdot \dfrac{3\pi}{a}=0\nonumber \]

\[{\sin \dfrac{3{\pi}x}{a}\ }{\cos \dfrac{3{\pi}x}{a}\ }=0\nonumber \]

Queremos no elegir valores de x que hagan\({\sin \dfrac{3{\pi}x}{a}\ }=0\), ya que eso significa que la densidad de probabilidad será cero. Sólo elegiremos los ceros de\({\cos \dfrac{3{\pi}x}{a}\ }\). Así que los posibles valores para x que hacen

\[{\cos \dfrac{3{\pi}x}{a}\ } =0 \nonumber \]

son

\[\dfrac{3px}{a}=\dfrac{2m+1}{2}p\ \ \ \ \ \ m=0,1,2,\dots \nonumber \]

\[x=\dfrac{\left(2m+1\right)a}{6}\nonumber \]

Solo elegimos\(m=0,1,2\) y no 3 porque\(m=3\) would give \(x=\dfrac{7a}{6}\) que está fuera de la caja. Entonces las ubicaciones son

\[x=\dfrac{a}{6}\nonumber \]

\[x=\dfrac{a}{2}\nonumber \]

\[x=\dfrac{5a}{6}\nonumber \]

3.13

Para qué rango\(L\) es posible\(\sigma_x\) dado:

\[\sigma_x = \sqrt{\langle x^2\rangle - \langle x \rangle^2}\nonumber \]

¿dónde\(L\) está la longitud de la caja 1-D? Pista: Recuerda que\(\sigma_x\) es la incertidumbre en la posición de una partícula en una caja.

Solución

Para una partícula en una caja:

\(\langle x \rangle = \dfrac{\text{L}}{2}\)

y

\(\langle x^2 \rangle = \dfrac{L^2}{3}-\dfrac{L^2}{2n^2\pi^2}\)

\(\sigma_x = \sqrt{\dfrac{L^2}{3}-\dfrac{L^2}{2n^2\pi^2} - (\dfrac{\text{L}}{2})^2}\)

Por inspección, sólo valores\(\sigma_x\) inferiores a los que\(L\) harán cierta esta afirmación.

3.14

Uso de la identidad trigonométrica

\[\cos(2x)=2\cos^{2}x-1\nonumber \]

demostrar que

\[\int_0^a 2 \cos^2 \dfrac{n\pi x}{a} -1 dx = 0\nonumber \]

\[\int_0^a \cos \dfrac{2n\pi x}{a} dx = 0\nonumber \]

\[\dfrac{a}{2n\pi} \sin(2n\pi) = 0\nonumber \]

3.18

Es la ondafunción\( \phi_n= \sqrt{\dfrac{2}{L}} \sin{(\dfrac{n\pi x}{L})} \) ortonormal terminada\( 0 \leq{x} \leq{L}\). Explica tu razonamiento.

Solución

Para que una función de onda sea ortonormal, tiene que satisfacer estas condiciones 1.) tiene que ser ortogonal y 2.) tiene que normalizarse.

Para demostrar que es ortogonal:

\[ \int_0^L \phi_m \phi\ast_n dx = 0\nonumber \]

cuando\(m\neq\) n

Para demostrar que la función de onda está normalizada debe seguir que

\[ \int_0^L \phi_n \phi\ast_n dx = 1 \nonumber \]

cuando m=n

Debido a que nuestra función de onda satisface ambas condiciones, es una función ortonormal.

Nos encontramos con que

\[\langle \psi_3 |\psi_3 \rangle = \int \limits _{-\infty}^{\infty} \dfrac{2}{L}(\sin\dfrac{3\pi x}{L})^2 dx = 1\nonumber \]

y

\[\langle \psi_4 |\psi_4 \rangle = \int \limits _{-\infty}^{\infty} \dfrac{2}{L}(\sin\dfrac{3\pi x}{L})(\sin\dfrac{4\pi x}{L}) dx = 0\nonumber \]

De la ortogonalidad, podemos aprender que si n no es igual a m, nuestro producto punto siempre será cero. Pero si n = m nuestro producto punto será igual a 1.

3.22

¿Cuál es el principio de incertidumbre de Heisenberg? La posición y el impulso siguen el principio de incertidumbre; ¿por qué o por qué no? Si lo hacen, ¿cuál es la incertidumbre mínima en la velocidad de un electrón si se sabe que está dentro de 1.5nm de un núcleo?

Solución

El Principio de Incertidumbre de Heisenberg establece que dos propiedades que siguen no se pueden medir simultáneamente con precisión arbitraria. La posición y el impulso siguen el principio. Si uno intentara conmutar a estos dos operadores, uno no obtendría cero y por lo tanto las propiedades no conmutan. Si no viajan, entonces no se pueden medir con precisión arbitraria.

Sabemos que

\[\Delta x \Delta p \geq \dfrac{\hbar}{2}\nonumber \]

Y que p = mv. Esto da

\[m\Delta x \Delta v \geq \dfrac{\hbar}{2}\nonumber \]

Se conoce la masa de un electrón es\(m_e \approx 9.1 \times 10^{-31}\;kg \). El problema también da\(\Delta x\) a ser 1.5 nm. A partir de aquí, se convierte en un tapón y chug para resolver\(\Delta v\).

\[\Delta v = 3.86 \times 10^4\nonumber \]

3.23

Describir las degeneraciones de una caja bidimensional cuyos dos lados tienen diferentes longitudes.

Solución

Las energías de una caja bidimensional viene dada por,

\[E = \dfrac{h^2}{8m} \left(\dfrac{n^{2}_{x}}{a^2}+\dfrac{n^{2}_{y}}{b^2}\right)\nonumber \]

Podemos ver que aunque\(a \ne b\), los niveles de energía no necesariamente serán degenerados.

3.26

¿Cuántos estados degenerados tienen los tres primeros niveles de energía para una partícula tridimensional en una caja si\(a=b=c\)?

3.27

Las moléculas de porfirina metálica se encuentran comúnmente en muchas proteínas y tiene la estructura general.

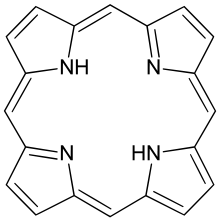
Esta molécula es plana, por lo que podemos aproximar electrones π como confinados dentro de un cuadrado. ¿Cuáles son los niveles de energía y las correspondientes degeneraciones de una partícula en un cuadrado de lado\(m\)? Las moléculas de porfirina tienen 18\(π\) electrones. Si la longitud de la molécula es de 850pm, ¿cuál es la menor absorción de energía de las moléculas de porfirina? (el valor experimental ≈ 17,000 cm ^-1）

Solución

El primer nivel de energía es E _(1,1,1) que no tiene degeneración.

El segundo estado energético es E _(2,1,1) =E _(1,2,1) =E _(1,1,2), por lo tanto tiene tres estados degenerados.

El tercer estado energético es E _(2,2,1) =E _(2,1,2) =E _(1,2,2), por lo que tiene tres estados degenerados.

3.26

Para una caja bidimensional de ancho\(w\) y alto\(h=\sqrt{a}w\), calcule todas las combinaciones de energía posibles entre\(E_{11}\) y\(E_{33}\) observe cualquier degeneración.

Solución

La energía de una partícula bidimensional en la caja tiene la forma,

\[E = \dfrac{h^2}{8m}\Bigg(\dfrac{n_x^2}{w^2}+\dfrac{n_y^2}{h^2}\Bigg)\nonumber \]

En este caso concreto\(h=\sqrt{a}w\) para que podamos simplificar el problema para,

\[E = \dfrac{h^2}{8m}\Bigg(\dfrac{n_x^2}{w^2}+\dfrac{2n_y^2}{w^2}\Bigg)\nonumber \]

Ahora podemos tabular el nivel de energía que indica degeneración.

\(E_{xy}\)	Degeneración	\(\dfrac{E8mw^2}{h^2}\)
\ (E_ {xy}\)” style="text-align:center; ">\(E_{11}\)	1	\ (\ dfrac {e8mw^2} {h^2}\)” style="text-align:center; ">3
\ (E_ {xy}\)” style="text-align:center; ">\(E_{12}\). \(E_{31}\)	2	\ (\ dfrac {e8mw^2} {h^2}\)” style="text-align:center; ">5
\ (E_ {xy}\)” style="text-align:center; ">\(E_{21}\)	1	\ (\ dfrac {e8mw^2} {h^2}\)” style="text-align:center; ">4
\ (E_ {xy}\)” style="text-align:center; ">\(E_{22}\)	1	\ (\ dfrac {e8mw^2} {h^2}\)” style="text-align:center; ">6
\ (E_ {xy}\)” style="text-align:center; ">\(E_{13}\). \(E_{32}\)	2	\ (\ dfrac {e8mw^2} {h^2}\)” style="text-align:center; ">7
\ (E_ {xy}\)” style="text-align:center; ">\(E_{23}\)	1	\ (\ dfrac {e8mw^2} {h^2}\)” style="text-align:center; ">8
\ (E_ {xy}\)” style="text-align:center; ">\(E_{33}\)	1	\ (\ dfrac {e8mw^2} {h^2}\)” style="text-align:center; ">9

3.32

En este problema, exploraremos el problema cuántico-mecánico de una partícula libre que no está restringida a una región finita. Recuerde que las energías cuantificadas de una partícula en una caja son un resultado directo de las condiciones de límite establecidas por los confines de la caja.

Cuando la energía potencial\(V(x)\) es igual a cero y la ecuación de Schrodinger se convierte

\[\dfrac{d^2\psi}{dx^2} + \dfrac{2mE}{\hbar^2}\psi(x) = 0\nonumber \]

Las dos soluciones a esta ecuación de Schrodinger son

\[\psi_1(x) = A_1e^{ikx}\nonumber \]

\[\psi_2(x) = A_2e^{-ikx}\nonumber \]

donde\[k = \dfrac{(2mE)^(1/2)}{\hbar}\nonumber \]

Demostrar eso\(\psi_1(x)\) y\(\psi_2(x)\) son solución a la ecuación de Schrodinger donde la energía potencial\(V(x)\) es igual a cero

Solución

Para demostrarlo\(\psi_1(x)\) y\(\psi_2(x)\) son soluciones hay que mencionar algunos valores

\[p = \hbar k → k = p/\hbar →k = \dfrac{(2mE)^{1/2}}{\hbar}\nonumber \]

Ahora tenemos

\[\dfrac{d^2Ae^{\pm ikx}}{dx^2} + \dfrac{2mE}{\hbar^2}Ae^{\pm ikx}= 0\nonumber \]

\[A(\pm ik)^2e^{\pm ikx} + \dfrac{2mE}{\hbar^2}Ae^{\pm ikx} = 0 → -k^2 + \dfrac{2mE}{\hbar^2} = 0 \nonumber \]

Cancelar los términos similares

Así,\(k = \dfrac{(2mE)^{1/2}}{\hbar}\), que es igual al\(k\) valor original

3.32

Demostrar que\(E\) tenía que ser un valor positivo, ya que cuando\(E\) es negativo la función de onda queda sin límites para\(x\) valores grandes

Solución

Si\(E\) < 0 entonces k se vuelve imaginario,\(k = ik\)

\(\psi = Ae^{\pm ikx} = Ae^{\pm i(ik)x} Ae^{\pm kx} \)

Para\(\psi_1(x) = A_1e^{-kx} \) esto explotará para x → -\(\infty\)

Para\(\psi_2(x) = A_2e^{kx} \) esto explotará para x →\(\infty\)

3.32

Con\(\hat{P}\)\(\psi_1(x)\) y\(\hat{P}\)\(\psi_2(x)\) como ecuaciones de valor propio, muestran que

\[\hat{P}\psi_1(x) = -i\hbar \dfrac{d\psi_1}{dx} = \hbar k\psi_1\nonumber \]

y

\[\hat{P}\psi_2(x) = -i\hbar \dfrac{d\psi_2}{dx} = -\hbar k\psi_2\nonumber \]

Solución

\[\hat{P}\psi_1(x) = -i\hbar \dfrac{d\psi_1}{dx} = -i\hbar \dfrac{d}{dx}A_1e^{+ikx} = -i\hbar A_1(ik)e^{ikx} = +\hbar kA_1e^{ikx} = + \hbar k\psi_1\nonumber \]

\[\hat{P}\psi_2(x) = -i\hbar \dfrac{d\psi_2}{dx} = -i\hbar \dfrac{d}{dx}A_2e^{-ikx} = -i\hbar A_2(-ik)e^{ikx} = -\hbar kA_1e^{-ikx} = -\hbar k\psi_2\nonumber \]

Ahora podemos demostrar que

\[E = \dfrac{p^2}{2m} = \dfrac{\pm (\hbar)^2}{2m} = \dfrac{\hbar^2 k^2}{2m}\nonumber \]

3.32

Demuestre eso\(\psi_1^{*}\psi_1(x) = A_1^{*}A_1 = \left | A_1\right |^2\) y aquello\(\psi_2^{*}\psi_2(x) = A_2^{*}A_2 = \left | A_2\right |^2\)

Solución

\[\begin{align*} \psi_1^{*}\psi_1(x) &= (A_1e^{ikx})^*A_1e^{ikx} \\[4pt] &= A_1^{*}A_1e^{-ikx}e^{ikx} \\[4pt] &= A_1^{*}A_1e^{-ikx+ikx} = A_1^{*}A_1e^{0} \\[4pt] &= A_1^{*}A_1\end{align*} \]

\[\begin{align*} \psi_2^{*}\psi_2(x) &= (A_2e^{-ikx})^*A_2e^{-ikx} \\[4pt] &= A_2^{*}A_2e^{ikx -ikx} \\[4pt] &= A_2^{*}A_2e^{0} = A_2^{*}A_2 \end{align*} \]

\(\psi\)tiene la misma probabilidad de estar en todas partes cuando\(\Delta x = \infty\) y\(\Delta p = 0 \)

3.33A

Suponiendo que una partícula se caracteriza por una onda estacionaria de Broglie, se le ocurre una ecuación para las energías permitidas de una partícula en una caja unidimensional.

Solución

La relación de Broglie es

\[\lambda = \dfrac{h}{p}\nonumber \]

Debido a que las olas son ondas estacionarias, caben en la caja un número integral de medias longitudes de onda o:

\[a = \dfrac{n\lambda}{2}\nonumber \]

y

\[a = \dfrac{nh}{2p}\nonumber \]

Resolviendo\(p\) rendimientos

\[p = \dfrac{nh}{2a}\nonumber \]

y la energía correspondiente es

\[E = \dfrac {mv^2}{2} = \dfrac{p^2}{2m} =\dfrac{1}{2m} \dfrac {n^2h^2}{4a^2} = \dfrac{n^2h^2}{8ma^2} \nonumber \]

3.33B

Derivar la velocidad más baja permitida para un protón en una caja de 10 ^-14 m de longitud (tamaño aproximado del núcleo), suponiendo que la partícula es descrita por una onda DeBroglie estacionaria.

Solución

La longitud de onda de Broglie es

\[λ = \dfrac{h}{p} = \dfrac{h}{m_pv}\nonumber \]

Para una onda unidimensional que tiene nodos en ambos extremos de una caja, puede caber un número entero de medias longitudes de onda, por lo que

\[n \left(\dfrac{λ}{2} \right) = L\nonumber \]

Sustituyendo esta longitud de onda en la relación de Broglie, one gets

\[\nu  = \dfrac{hn}{2m_L}\nonumber \]

la velocidad más baja permitida tendrá\(n = 1\)

\[\begin{align*} \nu &= \dfrac{(6.626 \times 10^{-34})(1)}{2 \times (1.67 \times 10^{-27})(10^{-14})} \\[4pt] &= 19.8 \times 10^6 m/s \end{align*} \]

3.33C

Si una partícula en una caja unidimensional se describe situando ondas de Broglie dentro de la caja, derivar una ecuación para las energías permitidas. Entonces usa esa ecuación para encontrar la energía de transición de n=1 a n=2 dado que la longitud de la caja es de 350pm y la masa de un electrón es\(9.109 \times 10^{-31} kg\).

Solución

La fórmula de Broglie es

\[\lambda=\dfrac{h}{p}\nonumber \]

Un número integral de medias longitudes de onda caben en la caja porque las ondas son ondas estacionarias así

\[\dfrac{n\lambda}{2}=a\nonumber \]

\[\dfrac{nh}{2p}=a\nonumber \]

Luego resolviendo para p

\[p=\dfrac{nh}{2a}\nonumber \]

Por lo tanto, la ecuación energética es

\[E=\dfrac{mv^2}{2}=\dfrac{p^2}{2,m}=\dfrac{1}{2m} \dfrac{n^2h^2}{4a^2}=\dfrac{n^2h^2}{8ma^2}\nonumber \]

Solo conéctate a la ecuación para encontrar la energía de transición

\[\Delta E=\dfrac{h^2}{8m_ea^2}(2^2-1^2)\nonumber \]

\[\Delta E=\dfrac{(6.626 \times 10^{-34} J \centerdot s)^2 (3) }{8(9.109 \times 10^{-31} kg)(350 \times 10^{-12}m)^2}\nonumber \]

\[\Delta E=1.47 \times 10^{-18}J \nonumber \]

3.35A

Considera las dos funciones de onda

\[\psi_n(x) = \sin\dfrac{n\pi x}{a} \nonumber \]

con n números pares y

\[\psi_n(x) = \cos\dfrac{n\pi x}{a} \nonumber\]

con n números impares.

Demostrar que las funciones de onda pueden ser simétricas y antisimétricas mediante el uso de la operación x a -x, a es una constante.

Dado que la ecuación de Schrödinger tiene la expresión:

\[\hat{H}(x)\psi_n(x) = E_n\psi_n(x) \nonumber\]

A través de la operación x a -x, la ecuación ahora se convierte en:

\[\hat{H}(-x)\psi_n(-x) = E_n\psi_n(-x) \nonumber\]

Demostrar que

\[\hat{H}(x) = \hat{H}(-x)\nonumber\]

es cierto para probar la ecuación de Schrödinger.

Solución

Sustituyendo\(x\) por\(-x\), por\(n\) números impares,

\[\hat{\psi}_n(-x) = \cos\dfrac{-n\pi x}{a} = \cos\dfrac{n\pi x}{a} = \hat{\psi}_n(x) \]

Para\(n\) números pares,

\[\hat{\psi}_n(-x) = sin\dfrac{-n\pi x}{a} = -sin\dfrac{n\pi x}{a} = -\hat{\psi}_n(x) \]

Así, la función de onda para el\(n\) número impar es simétrica y n números pares es antisimétrica.

Y,

\[\hat{H}(x) = -\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2} = \hat{H}(x)\]

\[\hat{H}(-x) = -\dfrac{\hbar^2}{2m}\dfrac{d^2}{d(-x)^2} = \hat{H}(x)\]

Por lo tanto,

\[\hat{H}(x) = \hat{H}(-x) \nonumber\]

y

\[\hat{H}(x) \nonumber \]

es una función par de\(x\).

3.35B

Demuestre que el Hamiltoniano para un Modelo de Rotor Rígido es impar.

Solución

\[ \hat{H}(x) = \hat{H}(-x)\nonumber \]

entonces

\[\hat{H}= -\dfrac{h^2}{4\pi \mu}\nabla^2\nonumber \]

\[\nabla^2 = \dfrac{d^2y}{dx^2} \dfrac{d^2y}{dy^2}\dfrac{d^2y}{dz^2}\nonumber \]

entonces

\[\dfrac{d^2y}{dx^2} (x) = 0\nonumber \]

y

\[\dfrac{d^2y}{dx^2}(-x) = 0\nonumber \]

entonces

\[\hat{H}(x) = 0\nonumber \]

y

\[\hat{H}(-x) = 0\nonumber \]

entonces

\[\hat{H}(x)= \hat{H}(-x)\nonumber \]