5.3: El oscilador armónico se aproxima a las vibraciones moleculares

Objetivos de aprendizaje

• Comprender la utilidad y los límites del uso del oscilador armónico cuántico como modelo de vibraciones moleculares

El oscilador armónico cuántico es uno de los sistemas modelo más importantes en mecánica cuántica. Esto se debe en parte al hecho de que una curva\(V(x)\) de potencial arbitraria suele aproximarse como un potencial armónico cerca de un punto de equilibrio estable. Además, es uno de los pocos sistemas cuántico-mecánicos para los que existe una solución analítica exacta. La resolución de otros potenciales normalmente requiere aproximaciones o enfoques numéricos para identificar los autoestados y valores propios correspondientes (es decir, las funciones de onda y las energías).

Una curva general de energía potencial (\(V(x)\)) para una vibración molecular se puede expandir como una serie Taylor

\[V(x) = V(x_0) + \left. \dfrac {d V(x)}{d x} \right|_{x_0}^{x} (x - x_0) + \left. \dfrac {1}{2!} \dfrac {d^2 V(x)}{d x^2} \right|_{x_0}^{x} (x - x_0)^2 + \ldots + \left. \dfrac {1}{n!} \dfrac {d^n V(x)}{d x^n} \right|_{x_0}^{x} (x - x_0)^n \label{5.3.1} \]

Es importante señalar que esta aproximación sólo es buena para\(x\) cerca\(x_0\), y eso\(x_0\) significa la distancia de enlace de equilibrio. \(V(x)\)a menudo (pero no siempre) se acorta al término cúbico y se puede reescribir como

\[V(x) = \dfrac {1}{2} kx^2 + \dfrac {1}{6} \gamma x^3 \label{5.3.2} \]

donde\(V(x_0) = 0\),\(k\) es la constante de fuerza armónica (término armónico), y\(\gamma\) es el primer término anarmónico (es decir, cúbico). Como demuestra la Figura 5.3.2 , el oscilador armónico (curva roja) es una buena aproximación para la energía potencial exacta de una vibración (curva azul).

Figura 5.3.1 : La vibración de la\(\ce{HCl}\) molécula es realmente un oscilador anarmónico, pero puede aproximarse como un oscilador armónico a bajas energías. En esta animación,\(\ce{HCl}\) está vibrando a nivel de\(E_3\) energía. \(D_0\)es la energía de disociación aquí, la longitud del\(r_0\) enlace, la energía\(V\) potencial. La energía se expresa en números de onda. La molécula de cloruro de hidrógeno se une al sistema de coordenadas para mostrar los cambios en la longitud del enlace en la curva. (CC BY-SA 3.0; Darekk2 vía Wikipedia).

Agregar perturbaciones anarmónicas al oscilador armónico (Ecuación\(\ref{5.3.2}\)) describe mejor las vibraciones moleculares. La oscilación anarmónica se define como la desviación de un sistema de la oscilación armónica, o un oscilador que no oscila en un simple movimiento armónico. La oscilación anarmónica se describe como la fuerza restauradora ya no es proporcional al desplazamiento. Agregar el término cúbico (Figura 5.3.2 ; curva verde) mejora la aproximación de la oscilación armónica especialmente bajo mayor desplazamiento desde el equilibrio.

Figura 5.3.2 : (izquierda) Desviación de aproximación simple del potencial armónico (curva roja) del potencial verdadero/exacto (curva azul) con término cúbico (verde). (derecha) Expansión con términos cuárticos positivos o negativos. (CC BY-NC; Ümit Kaya vía LibreTexts)

Naturalmente, agregar términos anarmónicos de orden superior, como términos cuárticos (Figura\(\PageIndex{2; right}\)) mejoran la aproximación. Casi todas las diatómicas tienen potenciales determinados experimentalmente para sus estados de energía más bajos. \(\ce{H2}\),\(\ce{Li2}\),\(\ce{O2}\)\(\ce{N2}\), y\(\ce{F2}\) con términos hasta\(n < 10\) determinados de Ecuación\(\ref{5.3.1}\).

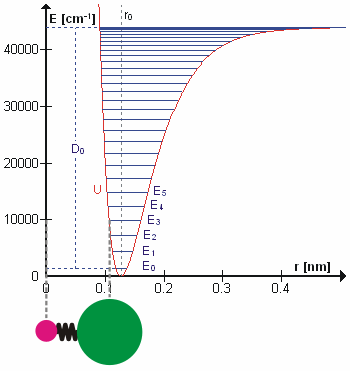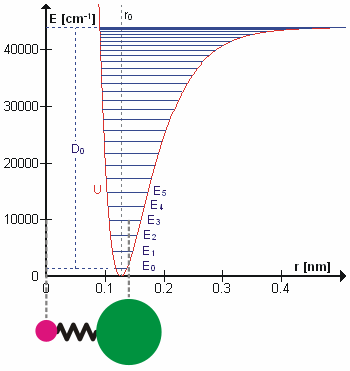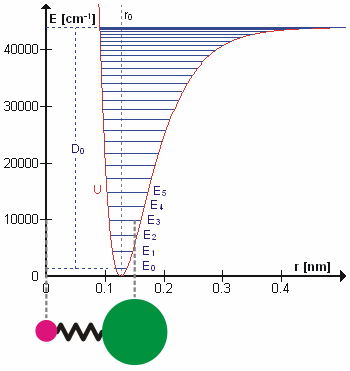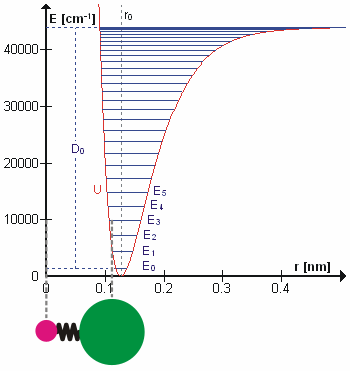
La figura 5.3.1 muestra el potencial general con niveles de energía calculados (numéricamente) (\(E_0\),\(E_1\) etc.). \(D_o\)es la energía de disociación, que es diferente de la profundidad del pozo\(D_e\). Estos niveles de energía vibracional de esta gráfica se pueden calcular usando el modelo de oscilador armónico (es decir, Ecuación 5.3.1 con la ecuación de Schrödinger) y tienen la forma general

\[ E_v = \left(v + \dfrac{1}{2}\right) v_e - \left(v + \dfrac{1}{2}\right)^2 v_e x_e + \left(v + \dfrac{1}{2}\right)^3 v_e y_e + \text{higher terms} \label{5.3.7} \]

donde\( v \) está el número cuántico vibracional\( x_e\) y y\( y_e\) son las constantes de anharmonía primera y segunda, respectivamente.

El\(v = 0\) nivel es el estado fundamental vibracional. Debido a que este potencial es menos confinante que una parábola utilizada en el oscilador armónico, los niveles de energía se vuelven menos espaciados a alta excitación (Figura 5.3.1 ; parte superior del potencial).

Limitaciones del modelo de oscilador armónico para vibraciones moleculares

La oscilación armónica es una gran aproximación de una vibración molecular, pero tiene limitaciones clave:

• Debido a la misma separación de energía, todas las transiciones ocurren a la misma frecuencia (es decir, espectro de una sola línea). Sin embargo experimentalmente muchas líneas se observan a menudo (llamadas armónicas).
• El oscilador armónico no predice la disociación de enlaces; no se puede romper sin importar cuánta energía se introduzca.

Los potenciales Morse son mejores Aproximaciones del Movimiento Vibracional

Un enfoque más potente que simplemente “parchear” la solución del oscilador armónico con correcciones anarmónicas es adoptar un potencial diferente (\(V(x)\)). Uno de esos enfoques es el potencial Morse, llamado así por el físico Philip M. Morse, y una mejor aproximación para la estructura vibracional de la molécula que el oscilador armónico porque incluye explícitamente los efectos de la ruptura de enlaces y da cuenta de la anarmónica de los vínculos reales (Figura 5.3.4 ).

Figura 5.3.4 : El potencial Morse (azul) y el potencial del oscilador armónico (verde). A diferencia de los niveles de energía del potencial del oscilador armónico, que están espaciados uniformemente por hω, el espaciamiento del nivel del potencial Morse disminuye a medida que la energía se acerca a la energía de disociación. La energía de disociación\(D_e\) is larger than the true energy required for dissociation \(D_0\) due to the zero point energy of the lowest (\(v = 0\)) vibrational level. de Wikipedia.

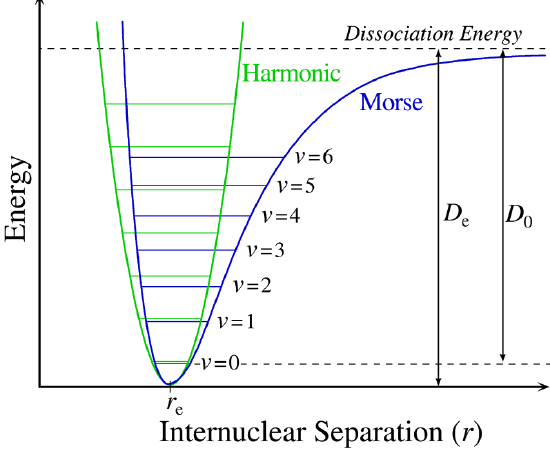
El Potencial Morse es una buena aproximación\(V(x)\) y es mejor cuando se busca una fórmula general para todos\(x\) desde 0 hasta\(\infty\), no solo aplicable para la región local alrededor del\(x_o\):

\[V(x) = D(1-e^{-\beta (x - x_0)})^2 \label{5.3.8} \]

con\(V(x = x_0) = 0\) y\(V(x = \infty) = D\).

El Potencial Morse (Figura 5.3.4 ) se acerca a cero en infinito\(r_e\) e igual a su\(-D_e\) mínimo (i.e.\(r=r_e\)). Muestra claramente que el potencial Morse es la combinación de un término de repulsión de corto alcance (\(r\)valores pequeños) y un término atractivo de largo alcance (\(r\)valores grandes).

Resolver la ecuación de Schrödinger con el Potencial Morse (Ecuación\ ref {5.3.8}) no es trivial, sino que se puede hacer analíticamente.

\[ \hat{H}|\psi \rangle = E_n | \psi \rangle \nonumber \]

con

\[ \begin{align} \hat{H} &= \hat{T} + \hat{V} \\[4pt] &= \dfrac{- \hbar ^2 d^2}{2m \;dx^2} + D(1-e^{-\beta (x - x_0)})^2 \label{5.3.9} \end{align} \]

Las soluciones y energías para el potencial Morse no serán utilizadas en este curso y no serán discutidas con más detalle.

Colaboradores y Atribuciones

• Peter Kelly (UCDavis)