5.9: El rotador rígido es un modelo para una molécula diatómica giratoria
- Page ID
- 80214
- Demostrar cómo usar el rotor regid 3D para describir moléculas diatómicas giratorias
- Demostrar cómo la espectroscopia de microondas puede acostumbrarse a caracterizar moléculas diatómicas giratorias
- Interpretar un espectro de microondas simple para una molécula diatómica
Para desarrollar una descripción de los estados rotacionales, consideraremos que la molécula es un objeto rígido, es decir, las longitudes del enlace son fijas y la molécula no puede vibrar. Este modelo para rotación se llama modelo de rotor rígido. Es una buena aproximación (aunque una molécula vibra a medida que gira, y los enlaces son elásticos en lugar de rígidos) porque la amplitud de la vibración es pequeña en comparación con la longitud del enlace.
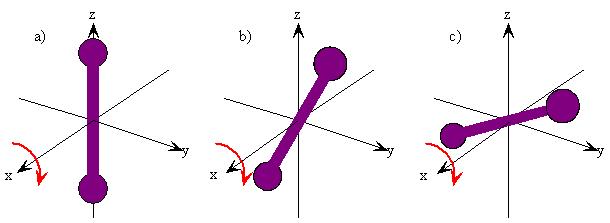
La rotación de un objeto rígido en el espacio es muy simple de visualizar. Recoge cualquier objeto y gírelo. Hay rotaciones ortogonales alrededor de cada uno de los tres ejes de coordenadas cartesianas así como hay traducciones ortogonales en cada una de las direcciones en el espacio tridimensional (Figuras 5.9.1 y 5.9.2 ). Se dice que estas rotaciones son ortogonales porque no se puede describir una rotación alrededor de un eje en términos de rotaciones alrededor de los otros ejes del mismo modo que no se puede describir una traslación a lo largo del eje x en términos de traslaciones a lo largo de los ejes y y z. Para una molécula lineal, el movimiento alrededor del eje interatómico (eje x) no se considera una rotación.
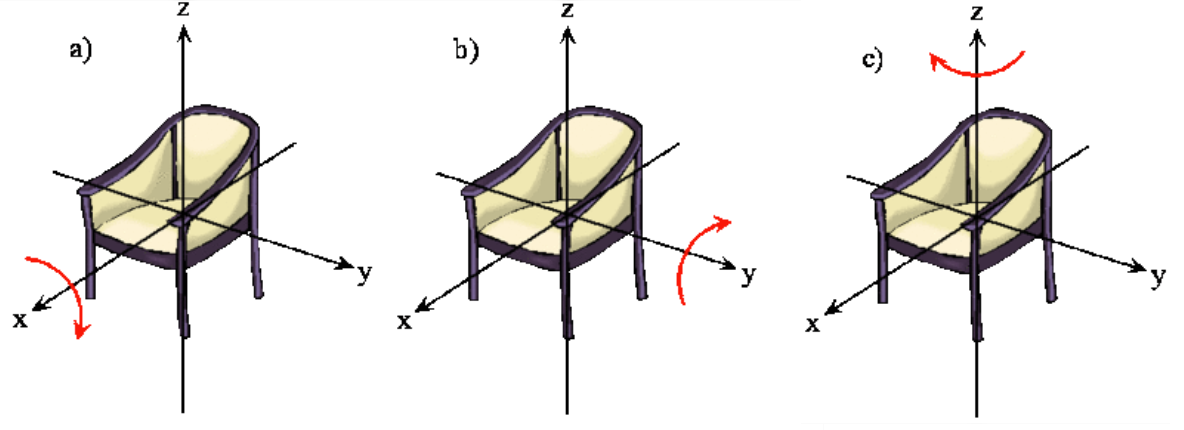
En esta sección examinamos los estados rotacionales de una molécula diatómica comparando la interpretación clásica del vector de momento angular con la interpretación probabilística de las funciones de onda de momento angular. Queremos responder a los siguientes tipos de preguntas. ¿Cómo se describe la orientación de una molécula diatómica giratoria en el espacio? ¿La molécula está rotando realmente? ¿Qué propiedades de la molécula se pueden observar físicamente? ¿De qué manera difiere la descripción mecánica cuántica de una molécula giratoria de la imagen clásica de una molécula giratoria?
Introducción a la Espectroscopia de Microondas
Los momentos dipolares eléctricos permanentes de las moléculas polares se pueden acoplar al campo eléctrico de la radiación electromagnética. Este acoplamiento induce transiciones entre los estados rotacionales de las moléculas. Las energías que están asociadas con estas transiciones se detectan en las regiones de infrarrojo lejano y microondas del espectro. Por ejemplo, el espectro de microondas para monóxido de carbono abarca un rango de frecuencias de 100 a 1200 GHz, lo que corresponde a 3 - 40\(cm^{-1}\).
Las reglas de selección para las transiciones rotacionales se derivan de la integral del momento de transición mediante el uso de las funciones armónicas esféricas y el operador de momento dipolo apropiado,\(\hat {\mu}\).
\[ \mu _T = \int Y_{J_f}^{m_f*} \hat {\mu} Y_{J_i}^{m_i} \sin \theta \,d \theta\, d \varphi \label{5.9.1a} \]
o en notación de braket
\[\mu _T = \langle Y_{J_f}^{m_f} | \hat {\mu} | Y_{J_i}^{m_i} \rangle \label{5.9.1b} \]
Evaluar la integral del momento de transición implica un poco de esfuerzo matemático. Esta evaluación revela que el momento de transición depende del cuadrado del momento dipolar de la molécula,\(\mu ^2\) y del número cuántico rotacional\(J\), del estado inicial en la transición,
\[\mu _T = \mu ^2 \dfrac {J + 1}{2J + 1} \label {5.9.2} \]
y que las reglas de selección para las transiciones rotacionales son
\[\Delta J = \pm 1 \label {5.9.3} \]
y
\[\Delta m_J = 0, \pm 1 \label {5.9.4} \]
Un fotón es absorbido\(\Delta J = +1\) y emitido para\(\Delta J = -1\).
Explica por qué tu horno microondas calienta el agua, pero no el aire. Pista: dibuje y compare estructuras de Lewis para componentes de aire y para agua.
Las energías de los niveles\(J^{th}\) rotacionales vienen dadas por
\[E_J = J(J + 1) \dfrac {\hbar ^2}{2I} \label{energy} \]
teniendo cada nivel de\(J^{th}\) energía una degeneración de\(2J+1\) debido a los diferentes\(m_J\) valores posibles.
Energías de transición de microondas
Las energías de transición para la absorción de la radiación están dadas por
\[\begin{align} E_{photon} &= \Delta E \\[4pt] &= E_f - E_i \label{5.9.5A} \\[4pt] &= h \nu \\[4pt] &= hc \bar {\nu} \label {5.9.5} \end{align} \]
Sustituir la relación de energía (Ecuación\ ref {energía}) en Ecuación\ ref {5.9.5A} da como resultado
\[\begin{align} E_{photon} &= E_f - E_i \\[4pt] &= J_f (J_f +1) \dfrac {\hbar ^2}{2I} - J_i (J_i +1) \dfrac {\hbar ^2}{2I} \label {5.9.6} \end{align} \]
con\(J_i\) y\(J_f\) representando los números cuánticos rotacionales de los niveles inicial (inferior) y final (superior) involucrados en la transición de absorción.
Dado que los espectroscopistas de microondas utilizan unidades de frecuencia y los espectroscopistas infrarrojos utilizan unidades de número de onda al describir los espectros rotacionales y los niveles de energía, ambos\(\nu\) y\(\bar {\nu}\) son importantes para calcular. Cuando añadimos las restricciones impuestas por las reglas de selección para identificar posibles transiciones,\(J_f\) en la Ecuación\ ref {5.9.6} se puede sustituir por\(J_i + 1\), ya que la regla de selección requiere\(J_f – J_i = 1\) para la absorción de un fotón (Ecuación\ ref {5.9.3}). La ecuación para las transiciones de absorción (Ecuación\ ref {5.9.6}) entonces se puede escribir en términos del único número cuántico\(J_i\) del estado inicial.
\[\begin{align} E_{photon} &= h \nu \\[4pt] &= hc \bar {\nu} \\[4pt] &= 2 (J_i + 1) \dfrac {\hbar ^2}{2I} \label {5.9.7} \end{align} \]
La ecuación\ ref {5.9.7} se puede reescribir como
\[E_{photon} = 2B (J_i+1) \nonumber \]
donde\(B\) es la constante rotacional para la molécula y se define en términos de la energía del fotón absorbido
\[B = \dfrac {\hbar ^2}{2I} \label {5.9.9} \]
A menudo, los espectroscopistas quieren expresar la constante rotacional en términos de frecuencia del fotón absorbido y lo hacen dividiendo la ecuación\(\ref{5.9.9}\) por\(h\)
\[ \begin{align} B (\text{in freq}) &= \dfrac{B}{h} \\[4pt] &= \dfrac {h}{8\pi^2 \mu r_0^2} \end{align} \nonumber \]
Más a menudo, los espectroscopistas quieren expresar la constante rotacional en términos de números de onda (\(\bar{\nu}\)) del fotón absorbido dividiendo la ecuación\(\ref{5.9.9}\) por\(hc\),
\[ \tilde{B} = \dfrac{B}{hc} = \dfrac {h}{8\pi^2 c \mu r_0^2} \label {5.9.8} \]
La constante de rotación depende de la distancia (\(R\)) y las masas de los átomos (a través de la masa reducida) de los núcleos en la molécula diatómica.
Construya un diagrama de nivel de energía rotacional para\(J = 0\)\(1\),\(2\) y agregue flechas para mostrar todas las transiciones permitidas entre estados que hacen que la radiación electromagnética sea absorbida o emitida.
Completa los pasos que van de Ecuación\(\ref{5.9.6}\) a Ecuación\(\ref{5.9.9}\) e identifica las unidades de\(B\) al final.
- Contestar
-
\ [\ begin {alinear*}
\ Delta E_ {fotón} &= E_ {f} - E {i}\\
E_ {r.rotor} &= J (J+1)\ frac {\ hbar^2} {2I}\\
E_ {fotón} = h_ {\ nu} = hc\ Widetilde {\ nu} &= J_F (J_f+1)\ frac {\ hbar^2} {2I} - J_i (J_i+1)\ frac {\ hbar^2} {2I}\\
J_F - J_i &= 1\\
J_f &= 1 + J_i\\
E_ {fotón} = h_ {\ nu} = hc\ Widetilde {\ nu} &= (1+J_i) (2+J_i)\ frac {\ hbar^2} {2I} - J_i (J_i+1)\ frac {\ hbar^2} {2I}\
&=\ frac {\ hbar^2} {2I} [2 + 3J_i + J_i^2 -j_i^2 - J_i]\\
&=\ frac {\ hbar^2} {2I} 2 (J_i+1)\\
&= 2B (J_i + 1)\ end {align*}\ nonumber\]Ahora hacemos un análisis dimensional estándar
\ [\ begin {align*} B &=\ frac {\ hbar^2} {2I}\ equiv\ izquierda [\ frac {kg m^2} {s^2}\ derecha] = [J]\\
\ frac {B} {h} = B (en freq.) &=\ frac {h} {8\ pi^2\ mu r_o^2}\ equiv\ izquierda [\ frac {1} {s}\ derecha]\
\ frac {B} {hc} =\ tilde ancho {B} &=\ frac {h} {8\ pi^2\ mu c r_o^2}\ equiv\ izquierda [\ frac {s} {m}\ derecha]\\
\ final {alinear*}\ nonumber\]
Los espectroscopistas infrarrojos utilizan unidades de números de onda. Reescribe los pasos que van de Ecuación\(\ref{5.9.6}\)\(\ref{5.9.9}\) a Ecuación para obtener expresiones para\(h\nu\) y\(B\) en unidades de números de onda. Tenga en cuenta que para convertir\(B\) en Hz a\(B\) in\(cm^{-1}\), simplemente divide el primero por\(c\).
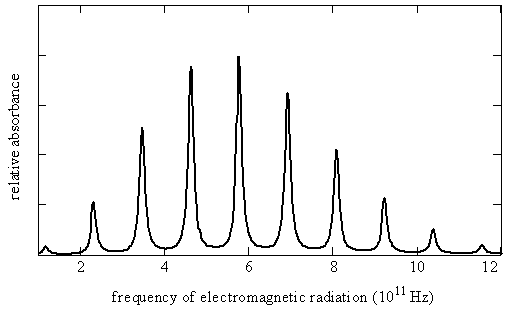
La figura 5.9.3 muestra el espectro rotacional como una serie de líneas casi equidistantes. Las posiciones de línea\(\nu _J\), los espaciamientos de línea y los coeficientes de absorción máximos (\(\gamma _{max}\), los coeficientes de absorción asociados a la posición de línea especificada) para cada línea en este espectro se dan aquí en la Tabla 5.9.1 .
|
|
|
|
|
|---|---|---|---|
| \(0 \rightarrow 1\) | \ (\ nu _J\) (MHz)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">115,271.21 | 0 | \ (\ gamma _ {max}\)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">0.0082 |
| \(1 \rightarrow 2\) | \ (\ nu _J\) (MHz)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">230,538.01 | 115,266.80 | \ (\ gamma _ {max}\)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">0.0533 |
| \(2 \rightarrow 3\) | \ (\ nu _J\) (MHz)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">345,795.99 | 115,257.99 | \ (\ gamma _ {max}\)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">0.1278 |
| \(3 \rightarrow 4\) | \ (\ nu _J\) (MHz)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">461,040.76 | 115,244.77 | \ (\ gamma _ {max}\)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">0.1878 |
| \(4 \rightarrow 5\) | \ (\ nu _J\) (MHz)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">576,267.91 | 115,227.15 | \ (\ gamma _ {max}\)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">0.1983 |
| \(6 \rightarrow 6\) | \ (\ nu _J\) (MHz)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">691,473.03 | 115,205.12 | \ (\ gamma _ {max}\)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">0.1618 |
| \(6 \rightarrow 7\) | \ (\ nu _J\) (MHz)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">806,651.78 | 115,178.68 | \ (\ gamma _ {max}\)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">0.1064 |
| \(7 \rightarrow 8\) | \ (\ nu _J\) (MHz)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">921,799.55 | 115,147.84 | \ (\ gamma _ {max}\)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">0.0576 |
| \(8 \rightarrow 9\) | \ (\ nu _J\) (MHz)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">1.036,912.14 | 115,112.59 | \ (\ gamma _ {max}\)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">0.0262 |
| \(9 \rightarrow 10\) | \ (\ nu _J\) (MHz)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">1,151,985.08 | 115,072.94 | \ (\ gamma _ {max}\)” style="text-align:center; vertical-align:middle;” class="lt-chem-13423">0.0103 |
Intentemos reproducir la Figura 5.9.3 a partir de los datos de la Tabla 5.9.1 usando la teoría cuántica que hemos desarrollado hasta ahora. La ecuación\(\ref{5.9.8}\) predice un patrón de líneas exactamente equiespaciadas. La transición de energía más baja es entre\(J_i = 0\) y\(J_f = 1\) así la primera línea del espectro aparece a una frecuencia de\(2B\). La siguiente transición es de\(J_i = 1\) a\(J_f = 2\) por lo que la segunda línea aparece en\(4B\). El espaciado de estas dos líneas es\(2B\). De hecho el espaciado de todas las líneas es\(2B\), lo cual es consistente con los datos experimentales en la Tabla 5.9.1 mostrando que las líneas están muy casi igualmente espaciadas. La diferencia entre el primer espaciado y el último espaciado es menor a 0.2%.
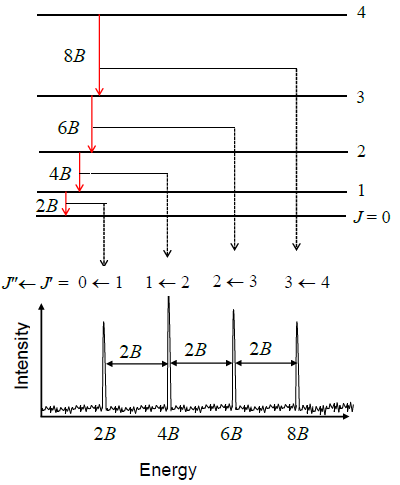
Utilice la ecuación\(\ref{5.9.8}\) para probar que el espaciado de dos líneas cualesquiera en un espectro rotacional es\(2B\), es decir, derivar:
\[\nu _{J_i + 1} - \nu _{J_i} = 2B \nonumber \]
- Contestar
-
Para probar la relación, evaluar el LHS. Primero, defina los términos:
\[ \nu_{J_{i}}=2B(J_{i}+1),\nu_{J_{i}+1}=2B((J_{i}+1)+1) \nonumber \]
Sustituir en la ecuación y evaluar:
\[2B((J_{i}+1)+1)-2B(J_{i}+1)=2B \nonumber \]
\[2B(J_{i}+1)+2B-2B(J_{i}+1)=2B \nonumber \]
\[2B=2B \nonumber \]
LHS es igual a RHS. Por lo tanto, el espaciado entre dos líneas cualesquiera es igual a\(2B\).
La molécula\(\ce{NaH}\) experimenta una transición rotacional de\(J=0\) a\(J=1\) cuando absorbe un fotón de frecuencia\(2.94 \times 10^{11} \ Hz\). ¿Cuál es la longitud del enlace de equilibrio de la molécula?
Solución
Utilizamos\(J=0\) en la fórmula para la frecuencia de transición
\[\nu =2B=\dfrac{\hbar}{2\pi I}=\dfrac{\hbar}{2\pi \mu R_{e}^{2}} \nonumber \]
Resolviendo para\(R_e\) da
\[R_e = \sqrt{\dfrac{\hbar}{2\pi \mu \nu}} \nonumber \]
La masa reducida viene dada por
\[\begin{align*}\mu &= \dfrac{m_{Na}m_H}{m_{Na}+m_H} \\[4pt] &=\dfrac{(22.989)(1.0078)}{22.989+1.0078}\\[4pt] &=0.9655\end{align*} \nonumber \]
que se encuentra en unidades de masa atómica o unidades relativas. Para convertir a kilogramos, necesitamos el factor de conversión\(1 \ au = 1.66\times 10^{-27} \ kg\). Multiplicando esto por\(0.9655\) gives a reduced mass of \(1.603\times 10^{-27} \ kg\). Sustituyendo por\(R_e\) da
\[\begin{align*} R_e &= \sqrt{\dfrac{(1.055 \times 10^{-34} \ J\cdot s)}{2\pi (1.603\times 10^{-27} \ kg)(2.94\times 10^{11} \ Hz)}}\\[4pt] &= 1.899\times 10^{-10} \ m \\[4pt] &=1.89 \ \stackrel{\circ}{A}\end{align*} \nonumber \]
Utilice la frecuencia de la\(J = 0\)\(J = 1\) transición observada para monóxido de carbono para determinar una longitud de enlace para\(^{12}C^{16}O\).
Solución
- J=0:\(v_{0}=115271.21\, MHz\)
- J = 1:\(v_{1}=230538.01\, MHz\)
\[\begin{align*} \Delta v &=230538.01 M H z-115271.21\, MHz \\[4pt] &=115266.8 MHz \\[4pt] &=1.153 \times 10^{11} Hz \\[4pt] &=\dfrac{\hbar}{2 \pi \mu R_{e}^2} \end{align*} \nonumber \]
La masa reducida es
\[\begin{align*} \mu &=\dfrac{m_{C} m_{O}}{m_{C}+m_{O}} \\[4pt] &=\frac{12.01 \times 16.00}{12.01+16.00} \\[4pt] &=6.86\, amu \end{align*} \nonumber \]
Convertir a kg
\[6.86 amu \, \left( \frac{1.661 \times 10^{-27} k g}{12 m u} \right) =1.139 \times 10^{-26} kg \nonumber \]
\[\begin{align*} R_{e} &=\sqrt{\frac{\hbar}{2 \pi \mu \Delta v}} \\[4pt] &= \sqrt{\frac{1.055 \times 10^{-34} J \cdot s}{2 \pi \cdot 1.139 \times 10^{-26} k g \cdot 1.153 \times 10^{11} H z}} \\[4pt] &=1.131 \times 10^{-10} \mathrm{m} \\[4pt] &=1.131\, \stackrel{\circ}{A} \end{align*} \nonumber \]
El estiramiento centrífugo del enlace a\(J\) medida que aumenta provoca la disminución en el espaciamiento entre las líneas en un espectro observado (Tabla 5.9.1 ). Esta disminución muestra que la molécula no es realmente un rotor rígido. A medida que el momento angular de rotación aumenta con el aumento\(J\), el enlace se estira. Este estiramiento aumenta el momento de inercia y disminuye la constante rotacional (Figura 5.9.5 ).
El efecto del estiramiento centrífugo es menor a\(J\) valores bajos, por lo que se\(B\) puede obtener una buena estimación de la\(J = 1\) transición\(J = 0\) a. A partir de\(B\), se puede obtener un valor para la longitud del enlace de la molécula ya que el momento de inercia que aparece en la definición de\(B\) (Ecuación\(\ref{5.9.9}\)) es la masa reducida por la longitud del enlace al cuadrado. Cuando se toma en cuenta cuantitativamente el estiramiento centrífugo, cuyo desarrollo está más allá del alcance de la discusión aquí, se puede obtener un valor muy preciso y preciso para B a partir de las frecuencias de transición observadas por su alta precisión. Las frecuencias de transición rotacional se reportan rutinariamente a 8 y 9 cifras significativas.
Como acabamos de ver, la teoría cuántica predice con éxito el espaciado entre líneas en un espectro rotacional. Una característica adicional del espectro son las intensidades de línea. Las líneas en un espectro rotacional no tienen todas la misma intensidad, como puede verse en la Figura 5.9.3 y la Tabla 5.9.1 . Esto está relacionado con las poblaciones de los estados inicial y final. Este aspecto de la espectroscopia se discutirá con más detalle en los siguientes capítulos
Colaboradores y Atribuciones
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski