6.4: Los orbitales atómicos de hidrógeno dependen de tres números cuánticos
- Page ID
- 80483
- Reconocer cómo varían los orbitales atómicos de hidrógeno en función de los tres números cuánticos primarios
Las soluciones a la ecuación de Schrödinger del átomo de hidrógeno discutidas anteriormente son funciones que son productos de una función armónica esférica y una función radial.
\[ \psi _{n, l, m_l } (r, \theta , \varphi) = \underbrace{R_{n,l} (r)}_{radial} \underbrace{ Y^{m_l}_l (\theta , \varphi)}_{angular} \label {6.1.14} \]
Las funciones de onda para el átomo de hidrógeno dependen de las tres variables\(r\),\(\theta\),\(\varphi \) y los tres números cuánticos\(n\),\(l\), y\(m_l\). Las variables dan la posición del electrón con respecto al protón en coordenadas esféricas. El cuadrado absoluto de la función de onda,, evaluado en\(| \psi (r, \theta , \varphi )|^2\),\(r\)\(\theta \), y\(\varphi\) da la densidad de probabilidad de encontrar el electrón dentro de un volumen diferencial\(d \tau\), centrado en la posición especificada por\(r\),\(\theta \), y\(\varphi\).
Evaluar las siguientes integrales
- \( \langle \psi (r, \theta, \varphi )| \psi (r, \theta , \varphi ) \rangle \nonumber\)
- \( \langle \psi (r, \theta, \varphi )| \psi (r', \theta' , \varphi' ) \rangle \nonumber\)
- Responder
-
a. Esta integral es igual a uno ya que\(\psi(r, \theta, \varphi)\) son autoestados normalizados.
b. Sin embargo, podemos evaluar explícitamente esta integral para cualquier par arbitrario de autoestados
\[\begin{align*} \langle\psi(r,\theta,\varphi)|\psi(r',\theta',\varphi')\rangle & = \int\limits_{all space}\psi^*(r,\theta,\varphi)\psi(r',\theta',\varphi')d\tau \\[4pt] &=\int\limits_{0}^{\infty} dr \int\limits_{0}^{\pi}d\theta\int\limits_{0}^{2\pi}d\varphi(r^2\sin(\theta))\overbrace{\psi*(r,\theta,\varphi)}^{R_{n,l}(r)Y_{l}^{m_l}(\theta,\varphi)}\overbrace{\psi(r,\theta,\varphi)}^{R_{n',l'}(r)Y_{l'}^{m'_l}(\theta,\varphi)} \\[4pt] &=\int \limits_{0}^{\infty} dr \int\limits_{0}^{\pi}d\theta \int \limits_{0}^{2\pi} d\varphi(r^2\sin(\theta))[R_{n,l}(r)Y_{l}^{m_l}(\theta,\varphi)][R_{n',l'}(r)Y_{l'}^{m'_l}(\theta,\varphi)] \\[4pt] &=\left[\int\limits_{0}^{\infty}r^2[R_{n,l}(r)R_{n',l'}(r)]dr\right]\left[\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\sin(\theta)[Y_{l}^{m_l}(\theta,\varphi)Y_{l'}^{m'_l}(\theta,\varphi)]d\theta d\varphi \right] \\[4pt] &=\langle R_{n,l}(r)|R_{n',l'}(r)\rangle\langle Y_{l}^{m_l}(\theta,\varphi)|Y_{l'}^{m'_l}(\theta,\varphi)\rangle \\[4pt] &=(\delta_{nn'}\delta_{ll'})(\delta_{ll'}\delta_{mm'}) =\delta_{nn'}\delta_{ll'}\delta_{mm'} \end{align*} \nonumber \]
Mientras que la parte a demuestra la normalidad de los autoestados, la parte b demuestra la ortogonalidad del autoestado (y también la normalidad).
Los números cuánticos tienen nombres:
- \(n\)se llama el número cuántico principal,
- \(l\)se llama el número cuántico de momento angular, y
- \(m_l\)se llama el número cuántico magnético porque la energía en un campo magnético depende de\(m_l\).
A menudo\(l\) se le llama el número cuántico azimutal porque es una consecuencia\(\theta\) de la ecuación, que involucra el ángulo azimutal\(\Theta \), refiriéndose al ángulo al cenit.
Parte Radial de la Función Onda
El comportamiento asintótico (es decir, lejos del núcleo) a la parte radial de la función ondulada es
\[ R_{asymptotic} (r) \sim \exp \left(-\dfrac {r}{n} a_0 \right) \label {6.1.15} \]
donde\(n\) resultará ser un número cuántico y\(a_0\) es el radio de Bohr (~52.9 pm). Tenga en cuenta que esta función disminuye exponencialmente con la distancia, de manera similar a la porción exponencial en descomposición de las funciones de onda del oscilador armónico, pero con una dependencia de distancia diferente,\(r\) vs\(r^2\).
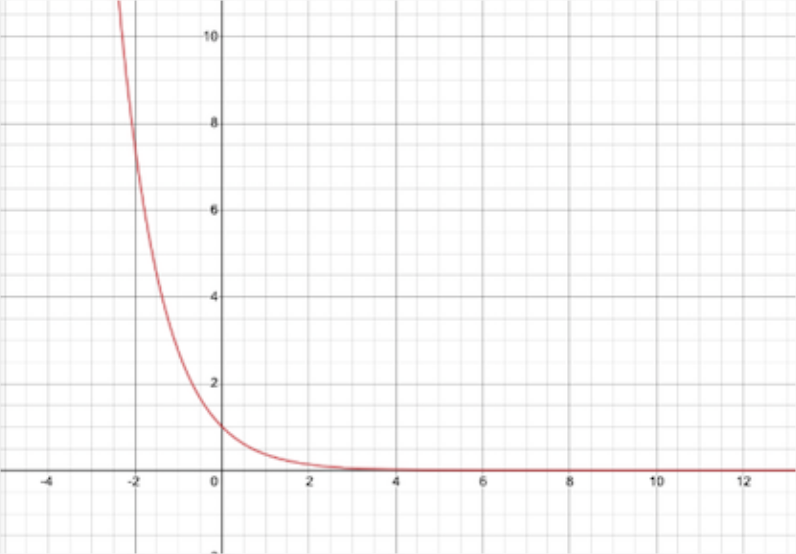
¿Qué sucede con la magnitud de a\(R_{asymptotic}(r)\) medida que la distancia\(r\) desde el protón se acerca al infinito? Esbozar una gráfica de la función,\(R_{asymptotic}(r)\). ¿Por qué podría esperarse este comportamiento para un electrón en un átomo de hidrógeno?
- Responder
-
\[R(r)=e^{-\frac{c}{n} a_{0}} \nonumber \]
A medida que\(r\) se acerca al infinito, la desintegración exponencial va a cero, esto es de esperar ya que la probabilidad de que un electrón se encuentre a una distancia infinita es casi nula también.
Los polinomios producidos por el truncamiento de la serie de potencias están relacionados con los polinomios asociados de Laguerre\(L_n , _l(r)\), donde el conjunto de\(c_i\) son coeficientes constantes.
\[L_{n, l} (r) = \sum _{r=0}^{n-l-1} c_i r^i \label {6.1.16} \]
Estos polinomios se identifican por dos índices o números cuánticos,\(n\) y\(l\). Las soluciones físicamente aceptables requieren\(n\) que sea mayor o igual a\(l +1\). El valor más pequeño para\(l\) es cero, por lo que el valor más pequeño para\(n\) es 1. El número cuántico de momento angular afecta la solución a la ecuación radial porque aparece en la ecuación diferencial radial, (Ecuación\(\ref{6.1.14}\)).
Las\(R(r)\) funciones que resuelven la Ecuación diferencial radial\(\ref{6.1.14}\), son productos de los polinomios asociados de Laguerre y el factor exponencial, multiplicado por un factor de normalización\((N_{n,l})\) y\(\left (\dfrac {r}{a_0} \right ) ^l\).
\[R (r) = N_{n,l} \left ( \dfrac {r}{a_0} \right ) ^l L_{n,l} (r) e^{-\frac {r}{n {a_0}}} \label {6.1.17} \]
El término exponencial decreciente supera al término polinómico creciente de modo que la función de onda general exhibe el enfoque deseado a cero a valores grandes de\(r\). Las primeras seis funciones radiales se proporcionan en la Tabla 6.4.1 . Obsérvese que las funciones en la tabla exhiben una dependencia\(Z\) del número atómico del núcleo. Como se discutió más adelante en este capítulo, otros sistemas de un electrón tienen estados electrónicos análogos a los del átomo de hidrógeno, y la inclusión de la carga en el núcleo permite que se utilicen las mismas funciones de onda para todos los sistemas de un electrón. Para hidrógeno,\(Z = 1\).
|
|
|
|
|---|---|---|
| 1 | \ (l\)” style="vertical-align:middle; ">0 | \ (R_ {n, l} (\ rho)\)” style="vertical-align:middle; ">\(2 \left (\dfrac {Z}{a_0} \right ) ^{3/2} e^{-\rho}\) |
| 2 | \ (l\)” style="vertical-align:middle; ">0 | \ (R_ {n, l} (\ rho)\)” style="vertical-align:middle; ">\( \dfrac {1}{2 \sqrt {2}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (2 - \rho) e^{-\rho/2}\) |
| 2 | \ (l\)” style="vertical-align:middle; ">1 | \ (R_ {n, l} (\ rho)\)” style="vertical-align:middle; ">\( \dfrac {1}{2 \sqrt {6}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} \rho e^{-\rho/2}\) |
| 3 | \ (l\)” style="vertical-align:middle; ">0 | \ (R_ {n, l} (\ rho)\)” style="vertical-align:middle; ">\( \dfrac {2}{81 \sqrt {3}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (27 - 18 \rho + 2\rho ^2) e^{-\rho/3}\) |
| 3 | \ (l\)” style="vertical-align:middle; ">1 | \ (R_ {n, l} (\ rho)\)” style="vertical-align:middle; ">\( \dfrac {1}{81 \sqrt {6}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (6 \rho + \rho ^2) e^{-\rho/3}\) |
| 3 | \ (l\)” style="vertical-align:middle; ">2 | \ (R_ {n, l} (\ rho)\)” style="vertical-align:middle; ">\( \dfrac {1}{81 \sqrt {30}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} \rho ^2 e^{-\rho/3}\) |
La restricción que\(n\) sea mayor o igual a\(l +1\) también resulta cuantificar la energía, produciendo la misma expresión cuantificada para los niveles de energía del átomo de hidrógeno que se obtuvo del modelo Bohr del átomo de hidrógeno.
\[ E_n = - \dfrac {\mu e^4}{8 \epsilon ^2_0 h^2 n^2} \nonumber \]
Es interesante comparar los resultados obtenidos al resolver la ecuación de Schrödinger con el modelo de Bohr del átomo de hidrógeno. Hay varias formas en que los modelos Schrödinger y Bohr difieren.
- Primero, y quizás lo más llamativo, el modelo de Schrödinger no produce órbitas bien definidas para el electrón. Las funciones de onda solo nos dan la probabilidad de que el electrón esté en varias direcciones y distancias del protón.
- Segundo, la cuantificación del momento angular es diferente a la propuesta por Bohr. Bohr propuso que el momento angular se cuantifica en unidades enteras de\(\hbar\), mientras que el modelo de Schrödinger conduce a un momento angular de\( \sqrt{(l (l +1)} \hbar\).
- Tercero, los números cuánticos aparecen de forma natural durante la solución de la ecuación de Schrödinger, mientras que Bohr tuvo que postular la existencia de estados energéticos cuantificados. Aunque más complejo, el modelo de Schrödinger conduce a una mejor correspondencia entre la teoría y el experimento en una gama de aplicaciones que no fue posible para el modelo de Bohr.
Explicar cómo la ecuación de Schrödinger lleva a la conclusión de que el momento angular del átomo de hidrógeno puede ser cero, y explicar cómo la existencia de tales estados con impulso angular cero contradice la idea de Bohr de que el electrón está orbitando alrededor del protón en el átomo de hidrógeno.
Los tres números cuánticos
Estos números cuánticos tienen valores específicos que están dictados por las restricciones físicas o condiciones de límite impuestas a la ecuación de Schrödinger: n debe ser un entero mayor que 0,\(l\) puede tener los valores de 0 a\(n‑1\), y\(m_l\) puede tener\(2l + 1\) valores que van desde\(-l\) ‑ hasta \(+l\)en pasos unitarios o enteros. Los valores del número cuántico\(l\) suelen estar codificados por una letra: s significa 0, p significa 1, d significa 2, f significa 3; los siguientes códigos continúan alfabéticamente (por ejemplo, g significa\(l = 4\)). Los números cuánticos especifican la cuantificación de cantidades físicas. Las energías discretas de los diferentes estados del átomo de hidrógeno vienen dadas por n, la magnitud del momento angular viene dada por\(l\), y un componente del momento angular (generalmente elegido por los químicos para ser el componente z) viene dado por\(m_l\). El número total de orbitales con un valor particular de\(n\) es\(n^2\).
Considerar varios valores para\(n\), y mostrar que el número de orbitales para cada uno\(n\) es\(n^2\).
Construir una tabla que resuma los valores permitidos para los números cuánticos\(n\),\(l\), y\(m_l\) para los niveles de energía 1 a 7 de hidrógeno.
La notación 3d especifica los números cuánticos para un electrón en el átomo de hidrógeno. ¿Cuáles son los valores para\(n\) y\(l\)? ¿Cuáles son los valores para la energía y el momento angular? ¿Cuáles son los valores posibles para el número cuántico magnético? ¿Cuáles son las posibles orientaciones para el vector de momento angular?
Colaboradores y Atribuciones
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski

