6.5: los orbitales s son esféricamente simétricos

Las funciones de onda del átomo de hidrógeno,\(\psi (r, \theta , \varphi )\), se llaman orbitales atómicos. Un orbital atómico es una función que describe un electrón en un átomo. La función de onda con\(n = 1\),\(l\) = 0 se llama orbital 1s, y un electrón que es descrito por esta función se dice que está “en” el orbital ls, es decir, tiene un estado orbital 1s. Las restricciones sobre n,\(l\), y\(m_l\) que se imponen durante la solución del átomo de hidrógeno La ecuación de Schrödinger explican por qué hay un solo orbital 1s, por qué hay tres orbitales 2p, cinco orbitales 3d, etc. Veremos cuando consideremos átomos de múltiples electrones, estas restricciones explican la características de la Tabla Periódica. En otras palabras, la Tabla Periódica es una manifestación del modelo de Schrödinger y las restricciones físicas impuestas para obtener las soluciones a la ecuación de Schrödinger para el átomo de hidrógeno.

Visualizar la variación de una función de onda electrónica con r,\(\theta\), y\(\varphi\) es importante porque el cuadrado absoluto de la función de onda representa la distribución de carga (densidad de probabilidad de electrones) en un átomo o molécula. La distribución de carga es fundamental para la química porque está relacionada con la reactividad química. Por ejemplo, una parte deficiente en electrones de una molécula es atraída por una región rica en electrones de otra molécula, y tales interacciones juegan un papel importante en interacciones químicas que van desde reacciones de sustitución y adición hasta plegamiento de proteínas y la interacción de sustratos con enzimas.

Podemos obtener una energía y una o más funciones de onda para cada valor de\(n\), el número cuántico principal, resolviendo la ecuación de Schrödinger para el átomo de hidrógeno. Un conocimiento de las funciones de onda, o amplitudes de probabilidad\(\psi_n\), nos permite calcular las distribuciones de probabilidad para el electrón en cualquier nivel cuántico dado. Cuando n = 1, la función de onda y la función de probabilidad derivada son independientes de la dirección y dependen únicamente de la distancia r entre el electrón y el núcleo. En la Figura 6.5.1 , trazamos ambos\(\psi_1\) y\(P_1\) versus\(r\), mostrando la variación en estas funciones a medida que el electrón se mueve cada vez más lejos del núcleo en cualquier dirección. (Estas y todas las gráficas siguientes se trazan en términos de la unidad atómica de longitud,\(a_0 = 0.529 \times 10^{-8}\, cm\).)

Figura 6.5.1 : La función de onda y la distribución de probabilidad como funciones de\(r\) para el\(n = 1\) nivel del átomo H. Las funciones y el radio r están en unidades atómicas en esta y siguientes figuras.

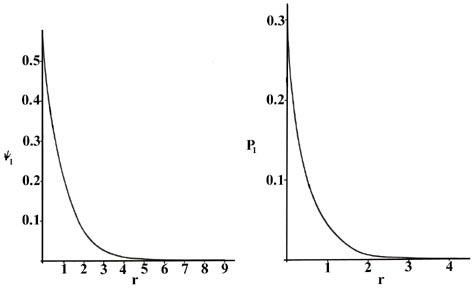
De nuevo se pueden dar dos interpretaciones a la\(P_1\) curva. Un experimento diseñado para detectar la posición del electrón con una incertidumbre mucho menor que el diámetro del átomo mismo (usando luz de longitud de onda corta), si se repite un gran número de veces, resultará en la Figura 6.5.1 para\(P_1\). Es decir, el electrón se detectará cerca del núcleo con mayor frecuencia y la probabilidad de observarlo a cierta distancia del núcleo disminuirá rápidamente con el aumento\(r\). El átomo se ionizará al realizar cada una de estas observaciones debido a que la energía de los fotones con una longitud de onda mucho menor a 10 ^-8 cm será mayor que\(K\), la cantidad de energía requerida para ionizar el átomo de hidrógeno. Si en el experimento se emplea luz con una longitud de onda comparable al diámetro del átomo, entonces el electrón no se excitará pero nuestro conocimiento de su posición será correspondientemente menos preciso. En estos experimentos, en los que no se cambia la energía del electrón, el electrón parecerá estar “manchado” y podemos interpretar\(P_1\) como dando la fracción de la carga electrónica total que se encuentra en cada elemento de pequeño volumen del espacio. (Recordemos que la adición del valor de P _n por cada elemento de pequeño volumen sobre todo el espacio suma a la unidad, es decir, un electrón y una carga electrónica).

Visualizar las funciones de onda y las distribuciones de carga es un desafío porque requiere examinar el comportamiento de una función de tres variables en el espacio tridimensional. Esta visualización se facilita al considerar las partes radial y angular por separado, pero trazar las partes radial y angular por separado no revela muy bien la forma de un orbital. La forma se puede revelar mejor en una gráfica de densidad de probabilidad. Para hacer tal trama tridimensional, divida el espacio en elementos de pequeño volumen, calcule\(\psi ^* \psi \) en el centro de cada elemento de volumen, y luego sombree, puntee o coloree ese elemento de volumen en proporción a la magnitud de\(\psi ^* \psi \).

También podríamos representar la distribución de carga negativa en el átomo de hidrógeno de la manera utilizada anteriormente para que el electrón confinado se mueva sobre un plano (Figura 6.5.2 ), mostrando la densidad de carga en un plano por medio de un mapa de contorno. Imagina un plano a través del átomo incluyendo el núcleo. La densidad se calcula en cada punto de este plano. Todos los puntos que tienen el mismo valor para la densidad de electrones en este plano están unidos por una línea de contorno (Figura 6.5.2 ). Dado que la densidad electrónica depende únicamente de r, la distancia desde el núcleo, y no de la dirección en el espacio, los contornos serán circulares. Un mapa de contorno es útil ya que indica la “forma” de la distribución de densidad.

Figura 6.5.2 : (a) Un mapa de contorno de la distribución de la densidad electrónica en un plano que contiene el núcleo para el\(n = 1\) nivel del átomo H. La distancia entre contornos adyacentes es de 1 au. Los números del lado izquierdo de cada contorno dan la densidad electrónica en au. Los números del lado derecho dan la fracción de la carga electrónica total que se encuentra dentro de una esfera de ese radio. Así, el 99% de la carga electrónica única del átomo de H se encuentra dentro de una esfera de radio 4 au (o diámetro =\(4.2 \times 10^{-8}\; cm\)). (b) Este es un perfil del mapa de contorno a lo largo de una línea que atraviesa el núcleo. Es, por supuesto, la misma que la dada anteriormente en la Figura 6.5.1 para\(P_1\), pero ahora trazada desde el núcleo en ambas direcciones.

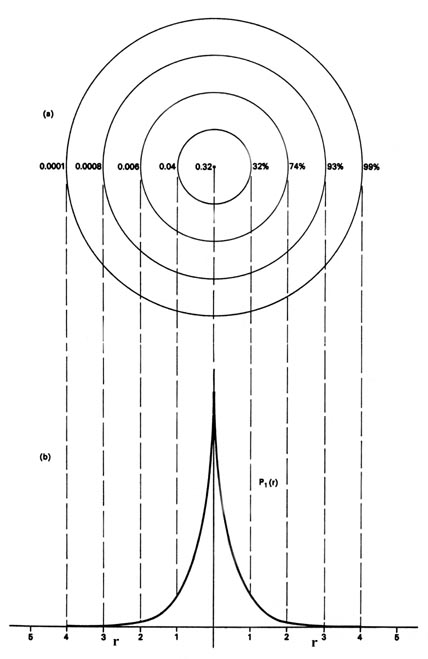
Cuando el electrón se encuentre en un nivel de energía definido nos referiremos a\(P_n\) las distribuciones como distribuciones de densidad electrónica, ya que describen la manera en que la carga electrónica total se distribuye en el espacio. La densidad electrónica se expresa en términos del número de cargas electrónicas por unidad de volumen de espacio, e ^-/V. El volumen V generalmente se expresa en unidades atómicas de longitud cúbica, y una unidad atómica de densidad electrónica es entonces e ^-/a ₀ ³. Para dar una idea del orden de magnitud de una unidad de densidad atómica, 1 au de densidad de carga e ^-/a ₀ ³ = 6.7 cargas electrónicas por Ångstrom cúbico. Es decir, un cubo con una longitud de\(0.52917 \times 10^{-8}\; cm\), si se llena uniformemente con una densidad de carga electrónica de 1 au, contendría 6.7 cargas electrónicas.

Por cada valor de la energía E _n, para el átomo de hidrógeno, hay una degeneración igual a\(n^2\). Por lo tanto, para n = 1, no hay más que una distribución orbital atómica y una densidad electrónica. Sin embargo, para n = 2, hay cuatro orbitales atómicos diferentes y cuatro distribuciones de densidad electrónica diferentes, todas las cuales poseen el mismo valor para la energía, E ₂. Así, para todos los valores del número cuántico principal n hay n ² formas diferentes en las que la carga electrónica puede distribuirse en el espacio tridimensional y aún así poseer el mismo valor para la energía. Por cada valor del número cuántico principal, uno de los orbitales atómicos posibles es independiente de la dirección y da una distribución esférica de densidad electrónica que puede ser representada por contornos circulares como se ha ejemplificado anteriormente para el caso de n = 1. Los otros orbitales atómicos para un valor dado de n exhiben una dependencia direccional y predicen distribuciones de densidad que no son esféricas sino que se concentran en planos o a lo largo de ciertos ejes. La dependencia angular de los orbitales atómicos para el átomo de hidrógeno y las formas de los contornos de las distribuciones de densidad electrónica correspondientes están íntimamente conectadas con el momento angular que posee el electrón.

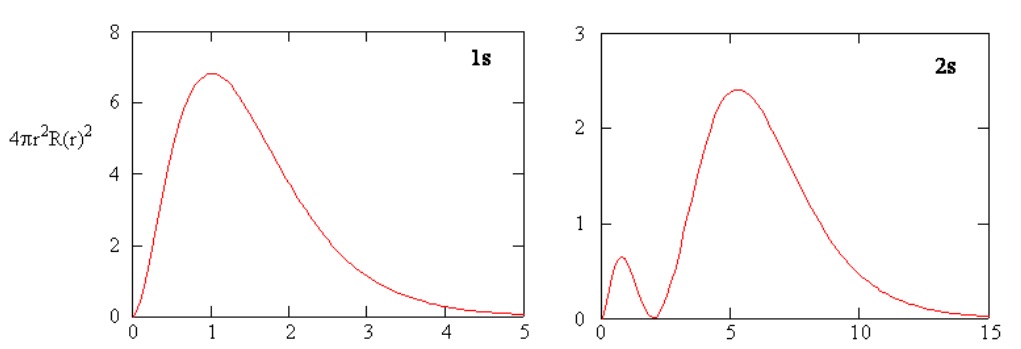
Los métodos para examinar separadamente las porciones radiales de los orbitales atómicos proporcionan información útil sobre la distribución de la densidad de carga dentro de los orbitales. Gráficas de las funciones radiales\(R(r)\),, para los orbitales 1s y 2s trazados en la Figura 6.5.3 . La función 1s en la Figura\(\PageIndex{3; left}\) comienza con un alto valor positivo en el núcleo y decae exponencialmente a esencialmente cero después de 5 radios Bohr. El alto valor en el núcleo puede ser sorprendente, pero como veremos más adelante, la probabilidad de encontrar un electrón en el núcleo es muy pequeña.

Figura 6.5.3 : Función radial,\(R(r)\), para los orbitales 1s y 2s. Para un gráfico interactivo haga clic aquí.

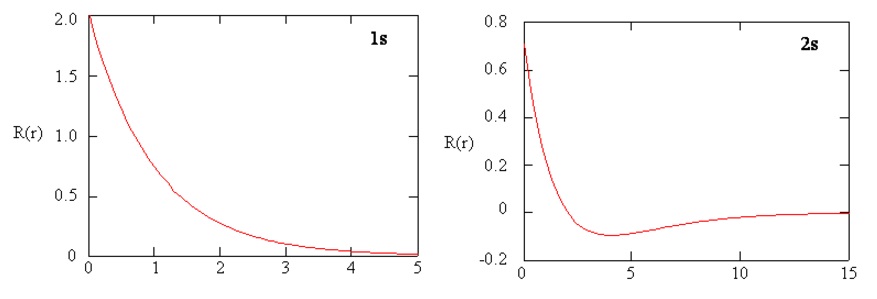
Siguiente Observe cómo la función radial para el orbital 2s, Figura\(\PageIndex{3; right}\), va a cero y se vuelve negativa. Este comportamiento revela la presencia de un nodo radial en la función. Un nodo radial ocurre cuando la función radial es igual a cero que no sea at\(r = 0\) o\(r = ∞\). Los nodos y los comportamientos limitantes de las funciones orbitales atómicas son útiles para identificar qué orbital se está describiendo por qué función de onda. Por ejemplo, todas las funciones s tienen valores de función de onda distintos de cero en\(r = 0\).

Ejercicio 6.5.1

Examinar las formas matemáticas de las funciones de onda radiales. ¿Qué característica de las funciones hace que algunas de ellas pasen a cero en el origen mientras que las funciones s no van a cero en el origen?

Ejercicio 6.5.2

¿Qué característica matemática de cada una de las funciones radiales controla el número de nodos radiales?

Ejercicio 6.5.3 : Nodos radiales

¿A qué valor de\(r\) ocurre el nodo radial 2s?

Ejercicio 6.5.4

Hacer una tabla que proporcione la energía, el número de nodos radiales, y el número de nodos angulares y el número total de nodos para cada función con\(n = 1\)\(n=2\), y\(n=3\). Identificar la relación entre la energía y el número de nodos. Identificar la relación entre el número de nodos radiales y el número de nodos angulares.

Responder

	Energía 1.Partícula en una Caja (h ^2 n ^2 /8m e L ^2) 2.Oscilador armónico ((n+0.5) ω) 3.Hidrógeno (-13.6ev/N ^2)	Número de nodos radiales (n-l-1)	Número de nodos angulares l = (n-1) l: s =0 p = 1 d = 2	Número total de nodos
n = 1	1. 6.02 *10 ^-38 J/L ^2 2. 1.5ω 3. -13.6 eV	-	0	0
n = 2	1. 6.02 *10 ^-38 J/L ^2 2. 2.5ω 3. -3.4 eV	para s: 1 para p: 0	para s: 0 para p: 1	1
n = 3	1. 6.02 *10 ^-38 J/L ^2 2. 3.5ω 3. 1.51 eV	para s: 2 para p: 1 para d: 0	para s: 0 para p:1 para d: 2	2

Para una partícula en una caja la energía es equivalente a\(E_n= 6.02 \times 10^{-38} n^2L^2\) donde\(n\) es cualquier valor mayor y no igual a 0 y L es la longitud de la caja.

Las densidades radiales de probabilidad para los orbitales atómicos 1s y 2s se representan en la Figura 6.5.4 .

Figura 6.5.4 : Densidades radiales (\(R (r) ^* R(r)\)) para los orbitales 1s y 2s.

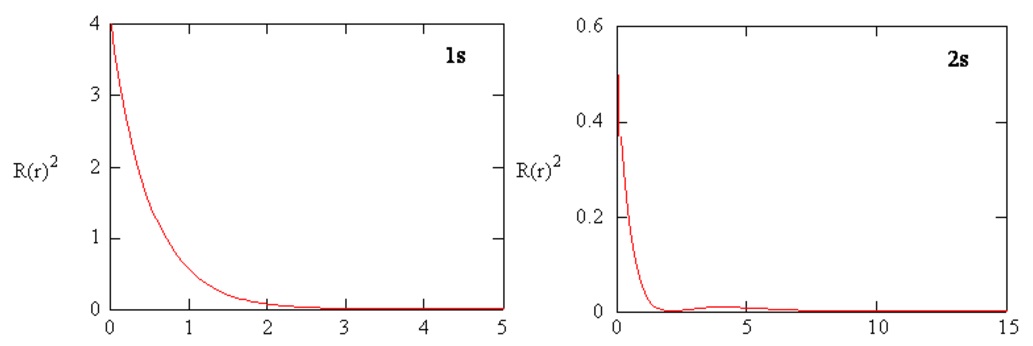
Funciones de distribución radial

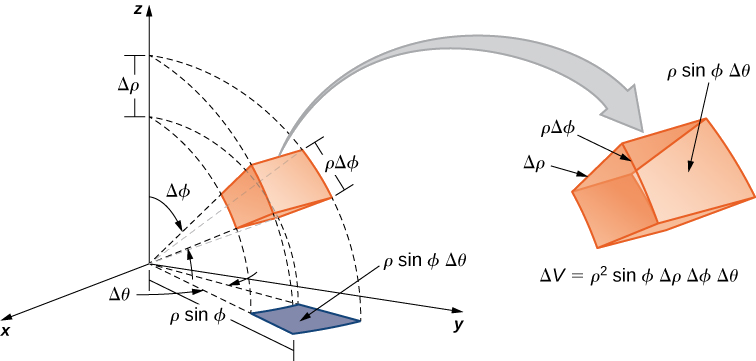
En lugar de considerar la cantidad de carga electrónica en un pequeño elemento particular del espacio, podemos determinar la cantidad total de carga que se encuentra dentro de una delgada capa esférica del espacio. Dado que la distribución es independiente de la dirección, considere sumar toda la densidad de carga que se encuentra dentro de un volumen de espacio delimitado por una esfera interna de radio\(r\) y una esfera concéntrica externa con un radio solo infinitesimalmente mayor, digamos\(r + \Delta r\). El área de la esfera interna es\(4\pi r^2\) y el grosor de la concha es\(\Delta r\). Así el volumen de la cáscara es\(4\pi r^2 \Delta r\) y el producto de este volumen y la densidad de carga P ₁ (r), que es la carga o número de electrones por unidad de volumen, es por lo tanto la cantidad total de carga electrónica que se encuentra entre las esferas de radio \(r\)y\(r + \Delta r\). Al producto\(4\pi r^2P_n\) se le da un nombre especial, la función de distribución radial.

Elemento de volumen para una concha en coordenadas esféricas

El lector puede preguntarse por qué el volumen del caparazón no se toma como:

\[ \dfrac{4}{3} \pi \left[ (r + \Delta r)^3 -r^3 \right] \nonumber \]

la diferencia de volumen entre dos esferas concéntricas. Cuando esta expresión para el volumen se expande, obtenemos

\[\dfrac{4}{3} \pi \left(3r^2 \Delta r + 3r \Delta r^2 + \Delta r^3\right) \nonumber \]

y para valores muy pequeños de\(\Delta r\) los\(\Delta r^3\) términos\(3r \Delta r^2\) y son despreciables en comparación con\(3r^2\Delta r\). Así, para valores pequeños de\(\Delta r\), las dos expresiones para el volumen del shell se acercan entre sí en valor y cuando\(\Delta r\) representa un pequeño incremento infinitesimal en\(r\) ellas son idénticas.

El elemento de volumen de una caja en coordenadas esféricas. (CC BY; OpenStax).

La función de distribución radial se representa en la Figura 6.5.5 para el estado fundamental del átomo de hidrógeno.

Figura 6.5.5 : La función de distribución radial para un átomo H. El valor de esta función a algún valor de r cuando se multiplica por\(\delta r\) da el número de cargas electrónicas dentro de la capa delgada del espacio que se encuentra entre las esferas de radio\(r\) y\(r + \delta r\).

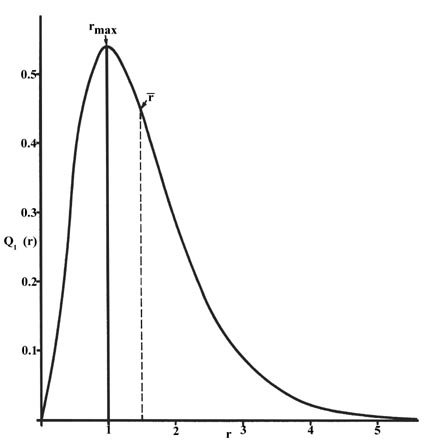
La curva pasa a través de zer o en\(r = 0\) sinc e la superficie de una esfera de radio cero es cero. A medida que aumenta el radio de la esfera, el volumen del espacio define d por\(4 \pi r^2Dr\) inc. Sin embargo, como se muestra en la Figura 6.5.4 , el valor absoluto de la densidad electrónica en un punto dado disminuye con\(r\) un nd la curva resultante debe pasar por un máximo. Este máximo ocurre a t\(r_{max} = a_0\). Así, más de la carga electrónica está presente a una distancia ce\(a_o\), ou t del núcleo que a cualquier otro valor de\(r\). Dado que la curva es asimétrica, el valor promedio de\(r\), denotado por\(\bar{r}\), no es igual t o\(r_{max}\). T el valor promedio de\(r\) se indica en la figura mediante una línea discontinua. Una “imagen” de la distribución de la densidad de electrones para el electrón en\(n = 1\) el nivel l del átomo de hidrógeno sería una bola de carga esférica, densa alrededor del núcleo y cada vez más difusa a medida que aumenta el valor de f\(r\).

La función de distribución radial da la densidad de probabilidad para que un electrón se encuentre en cualquier parte de la superficie de una esfera ubicada a una\(r\) distancia del protón. Dado que el área de una superficie esférica es\(4 \pi r^2\), la función de distribución radial viene dada por\(4 \pi r^2 R(r) ^* R(r)\).

Las funciones de distribución radial se muestran en la Figura 6.5.6 . A valores pequeños de\(r\), la función de distribución radial es baja debido a que el área de superficie pequeña para radios pequeños modula el valor alto de la función de densidad de probabilidad radial cerca del núcleo. A medida que aumentamos\(r\), el área de superficie asociada a un valor dado de\(r\) aumenta, y el\(r^2\) término hace que la función de distribución radial aumente a pesar de que la densidad de probabilidad radial comienza a disminuir. A grandes valores de\(r\), la decadencia exponencial de la función radial supera el aumento causado por el\(r^2\) término y la función de distribución radial disminuye.

Figura 6.5.6 : La función de distribución radial (\(4 \pi r^2 R (r) ^* R(r)\)) para los orbitales 1s y 2s. Compare con las funciones radiales en la Figura 6.5.3 o las densidades radiales en la Figura 6.5.4 . Para un gráfico interactivo haga clic aquí.

Ejemplo 6.5.1 :

Calcular la probabilidad de encontrar un electrón de hidrógeno de 1s que se encuentra\(2a_o\) a distancia del núcleo.

Solución

Tenga en cuenta la función de onda del hidrógeno 1s orbital que es

\[ψ_{100}= \dfrac{1}{\sqrt{π}} \left(\dfrac{1}{a_0}\right)^{3/2} e^{-\rho} \nonumber \]

con\(\rho=\dfrac{r}{a_0} \).

La probabilidad de encontrar el electrón a\(2a_0\) distancia del núcleo será:

\[prob= \underbrace{\int_{0}^{\pi} \sin \theta \, d\theta}_{over\, \theta} \, \overbrace{ \dfrac{1}{\pi a_0^3} \int_{0}^{2a_0} r^2 e^{-2r/a_0} dr}^{over\, r} \, \underbrace{ \int_{0}^{2\pi} d\phi }_{over\, \phi } \nonumber \]

Desde\(\int_0^{\pi} \sin \theta d\theta=2\) y\( \int_0^{2\pi} d\phi=2\pi\), tenemos

\[ \begin{align*} prob &=2 \times 2\pi \times \dfrac{1}{\pi a_0^3} \int_0^2a_0 (-a_0/2)r^2 d e^{-2r/a_0} \\[4pt]&=\dfrac{4}{a_0^3}\left(-\dfrac{a_0}{2}\right) (r^2 e^{-2r/a_0} |_0^{2a_0} - \int_0^{2a_0} 2r e^{-2r/a_0} dr) \\[4pt]&= -\dfrac{2}{a_0^2} [(2a_0)^2 e^{-4}-0-2\int_0^{2a_0} r \left(-\dfrac{a_0}{2}\right) d e^{-2r/a_0} ] \\[4pt]&=-\dfrac{2}{a_0^2}4a_0^2 e^{-4} +\dfrac{4}{a_0^2}(-\dfrac{a_0}{2}) (r e^{-2r/a_0} |_0^{2a_0}-\int_0^{2a_0} e^{-2r/a_0} dr ) \\[4pt]&=-8e^{-4}-\dfrac{2}{a_0} \left[2a_0e^{-4}-0-(-\dfrac{a_0}{2})e^{-2r/a_0} |_0^{2a_0} \right] \\[4pt]&=-8e^{-4}-4e^{-4}-e^{2r/a_0} |_0^{2a_0} \\[4pt]&=-12 e^{-4}-(e^{-4}-1)=1-13e^{-4}=0.762 \end{align*} \nonumber \]

Hay un 76.2% de probabilidad de que los electrones estén dentro\(2a_o\) del núcleo en el propio estado 1s.

Resumen

Esto completa la descripción del estado más estable del átomo de hidrógeno, el estado para el cual\(n = 1\). Antes de continuar con una discusión sobre los estados excitados del átomo de hidrógeno debemos introducir un nuevo término. Cuando la energía del electrón se incrementa a otro de los valores permitidos, correspondiente a un nuevo valor para\(n\),\(y_n\) y\(P_n\) cambiar también. A las funciones de onda\(y_n\) para el átomo de hidrógeno se les da un nombre especial, orbitales atómicos, porque juegan un papel tan importante en todas nuestras futuras discusiones sobre la estructura electrónica de los átomos. En general la palabra orbital es el nombre que se le da a una función de onda que determina el movimiento de un solo electrón. Si la función de onda de un electrón es para un sistema atómico, se llama orbital atómico.

No confundir la palabra orbital con la palabra clásica y la noción de órbita. Primero, una órbita implica el conocimiento de una trayectoria o trayectoria definida para una partícula a través del espacio que en sí misma no es posible para un electrón. En segundo lugar, un orbital, como la función de onda, no tiene realidad física sino que es una función matemática que cuando está al cuadrado da la distribución de densidad electrónica físicamente medible.

Colaboradores y Atribuciones

• Dr. Richard F.W. Bader  (Professor of Chemistry / McMaster University)

• Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski