7.2: Método Variacional Lineal y Determinante Secular
- Page ID
- 80387
- Entender cómo se puede ampliar el método variacional para incluir funciones de onda de prueba que son una combinación lineal de funciones con coeficientes que son los parámetros a variar.
- Ser capaz de construir ecuaciones seculares para resolver el procedimiento de minimización intrínseco al enfoque del método variacional.
- Mapear las ecuaciones seculares en el determinante secular
- Comprender cómo la aproximación de Combinación Lineal de Orbital Atómico (LCAO) es una aplicación específica del método variacional lineal.
Un tipo especial de variación ampliamente utilizado en el estudio de las moléculas es la llamada función de variación lineal, donde la función de onda de prueba es una combinación lineal de funciones\(N\) linealmente independientes (a menudo orbitales atómicos) que no los valores propios de los hamiltonianos (ya que no son conocido). Por ejemplo
\[| \psi_{trial} \rangle = \sum_{j=1}^N a_j |\phi_j \rangle \label{Ex1} \]
y
\[ \langle \psi_{trial} | = \sum_{j=1}^N a_j^* \langle \phi_j | \label{Ex2} \]
En estos casos, se dice que se está realizando un cálculo de 'variación lineal'.
El conjunto de funciones {función base\(\phi_j\)} are called the 'variable lineal' y no son más que miembros de un conjunto de funciones que son convenientes para tratar. Sin embargo, normalmente no son arbitrarios y generalmente se seleccionan para abordar propiedades específicas del sistema:
- obedecer todas las condiciones límite que\(| \psi _{trial} \rangle\) obedece el estado exacto,
- ser funciones de las mismas coordenadas que\(| \psi _{trial} \rangle\),
- ser de la misma simetría que\(| \psi _{trial} \rangle\), y
- para ser conveniente evaluar términos hamiltonianos elem ents\(\langle \phi_i|H|\phi_j \rangle\).
Más allá de estas condiciones, nada más que el esfuerzo puede limitar la selección y el número de tales funciones de base en las expansiones en Ecuaciones\(\ref{Ex1}\) y\(\ref{Ex2}\).
Como se discute en la Sección 7.1, la energía variacional para una función de onda de ensayo generalizada es
\[ E_{trial} = \dfrac{ \langle \psi _{trial}| \hat {H} | \psi _{trial} \rangle}{\langle \psi _{trial} | \psi _{trial} \rangle} \label{7.1.8} \]
Sustituir las Ecuaciones\ ref {Ex1} y\ ref {Ex2} en la Ecuación\ ref {7.1.8} implica abordar el numerador y el denominador individualmente. Para el numerador, la integral se puede ampliar así:
\[\begin{align} \langle\psi_{trial} |H| \psi_{trial} \rangle &= \sum_{i}^{N} \sum_{j} ^{N}a_i^{*} a_j \langle \phi_i|H|\phi_j \rangle. \\[4pt] &= \sum_{i,\,j} ^{N,\,N}a_i^{*} a_j \langle \phi_i|H|\phi_j \rangle. \label{MatrixElement}\end{align} \]
Podemos reescribir la siguiente integral en la Ecuación\ ref {MatrixElement} como una función de los elementos básicos (no la función de onda de prueba) como
\[ H_{ij} = \langle \phi_i|H|\phi_j \rangle \nonumber \]
Entonces el numerador del lado derecho de la Ecuación\ ref {7.1.8} se convierte
\[\langle\psi_{trial} |H| \psi_{trial} \rangle = \sum_{i,\,j} ^{N,\,N}a_i^{*} a_j H_{ij} \label{numerator} \]
Del mismo modo, se puede ampliar el denominador del lado derecho de la Ecuación\ ref {7.1.8}
\[\langle \psi_{trial}|\psi_{trial} \rangle = \sum_{i,\,j} ^{N,\,N}a_i^{*} a_j \langle \phi_i | \phi_j \rangle \label{overlap} \]
A menudo simplificamos las integrales en el lado derecho de la ecuación\ ref {overlap} como
\[ S_{ij} = \langle \phi_i|\phi_j \rangle \nonumber \]
donde\(S_{ij}\) se superponen integrales entre los diferentes {\(\phi_j\)} basis functions. La ecuación\ ref {superposición} se expresa así como
\[\langle \psi_{trial}|\psi_{trial} \rangle = \sum_{i,\,j} ^{N,\,N}a_i^{*} a_j S_{ij} \label{denominator} \]
No hay una regla explícita de que el {\(\phi_j\)} functions have to be orthogonal or normalized functions, although they often are selected that way for convenience. Therefore, a priori,\(S_{ij}\)no tiene que ser\(\delta_{ij}\).
Sustituir las ecuaciones\ ref {numerador} y\ ref {denominador} en la fórmula de energía variacional (Ecuación\ ref {7.1.8}) da como resultado
\[ E_{trial} = \dfrac{ \displaystyle \sum_{i,\,j} ^{N,\,N}a_i^{*} a_j H_{ij} }{ \displaystyle \sum_{i,\,j} ^{N,\,N}a_i^{*} a_j S_{ij} } \label{Var} \]
Para una función de onda de ensayo como la Ecuación\ ref {Ex1}, la energía variacional depende cuadráticamente de los\(a_j\) coeficientes de 'variación lineal'. Estos coeficientes se pueden variar al igual que los parámetros en las funciones de prueba de la Sección 7.1 para encontrar la función de onda de prueba optimizada (\(| \psi_{trial} \rangle\)) que se aproxime a la verdadera función de onda (\(| \psi \rangle\)) que no podemos resolver analíticamente.
Minimización de la Energía Variacional
La expresión para energía variacional (Ecuación\ ref {Var}) puede ser reordenada
\[E_{trial} \sum_{i,\,j} ^{N,\,N} a_i^*a_j S_{ij} = \sum_{i,\,j} ^{N,\,N} a_i^* a_j H_{ij} \label{7.2.9} \]
Los coeficientes óptimos se encuentran buscando mínimos en el paisaje energético variacional abarcado por la variación de los\(\{a_i\}\) coeficientes (Figura 7.2.1 ).
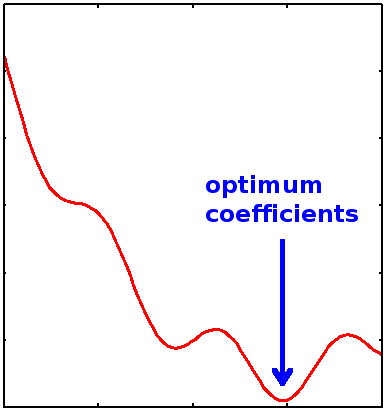
Queremos minimizar la energía con respecto a los coeficientes lineales\(\{a_i\}\), lo que requiere que
\[\dfrac{\partial E_{trial}}{\partial a_i}= 0 \nonumber \]
para todos\(i\).
Diferenciar ambos lados de la ecuación\(\ref{7.2.9}\) para el\(k^{th}\) coeficiente da,
\[ \dfrac{\partial E_{trial}}{\partial a_k} \sum_{i,\,j} ^{N,\,N} a_i^*a_j S_{ij}+ E_{trial} \sum_i \sum_j \left[ \dfrac{ \partial a_i^*}{\partial a_k} a_j + \dfrac {\partial a_j}{\partial a_k} a_i^* \right ]S_{ij} = \sum_{i,\,j} ^{N,\,N} \left [ \dfrac{\partial a_i^*}{\partial a_k} a_j + \dfrac{ \partial a_j}{\partial a_k}a_i^* \right] H_{ij} \label{7.2.10} \]
Dado que los coeficientes son independientes
\[\dfrac{\partial a_i^*}{ \partial a_k} = \delta_{ik} \nonumber \]
y
\[S_{ij} = S_{ji} \nonumber \]
y también dado que el hamiltoniano es un operador hermitiano (ver abajo)
\[H_{ij} =H_{ji} \nonumber \]
entonces Ecuación\(\ref{7.2.10}\) simplifica a
\[ \dfrac{\partial E_{trial}}{\partial a_k} \sum_i \sum_j a_i^*a_j S_{ij}+ 2E_{trial} \sum_i a_i S_{ik} = 2 \sum_i a_i H_{ik} \label{7.2.11} \]
En la energía variacional mínima, cuando
\[\dfrac{\partial E_{trial}}{\partial a_k} = 0 \nonumber \]
entonces Ecuación\(\ref{7.2.11}\) da
\[ {\sum _i^N a_i (H_{ik}–E_{trial} S_{ik}) = 0} \label{7.2.12} \]
para todos\(k\). Las ecuaciones en\(\ref{7.2.12}\) se llaman las Ecuaciones Seculares.
Los operadores hermitianos son operadores que satisfacen la fórmula general
\[ \langle \phi_i | \hat{A} | \phi_j \rangle = \langle \phi_j | \hat{A} | \phi_i \rangle \label{Herm1} \]
Si se cumple esa condición, entonces\(\hat{A}\) es un operador hermitiano. Para cualquier operador que genere un valor propio real (por ejemplo, observables), entonces ese operador es hermitiano. El hamiltoniano\(\hat{H}\) cumple con la condición de operador hermitiano. La ecuación\ ref {Herm1} se puede reescribir como
\[A_{ij} =A_{ji}^* \nonumber \]
donde
\[A_{ij} = \langle \phi_i | \hat{A} | \phi_j \rangle \nonumber \]
y
\[A_{ji} = \langle \phi_j | \hat{A} | \phi_i \rangle \nonumber \]
Por lo tanto, cuando se aplica al operador hamiltoniano
\[H_{ij}^* =H_{ji}. \nonumber \]
Si las funciones\(\{|\phi_j\rangle \}\) son ortonormales, entonces la matriz de superposición se\(S\) reduce a la matriz unitaria (una en la diagonal y cero en cada otro lugar) y las Ecuaciones Seculares en la Ecuación\ ref {7.2.12} se reducen a la forma Eigenvalue más familiar:
\[ \sum\limits_i^N H_{ij}a_j = E_{trial} a_i .\label{seceq2} \]
De ahí que la ecuación secular, en cualquiera de sus formas, tenga tantos valores propios\(E_i\) y vectores propios {\(C_{ij}\)} como la dimensión de la\(H_{ij}\) matriz como las funciones en\(| \psi_{trail} \rangle\) (Ejemplo\ ref {Ex1}). También se puede demostrar que entre pares sucesivos de los valores propios obtenidos al resolver el problema secular debe ocurrir al menos un valor propio exacto (es decir\( E_{i+1} > E_{exact} > E_i\), para todos i). Esta observación es referida como 'el teorema de horquillado'.
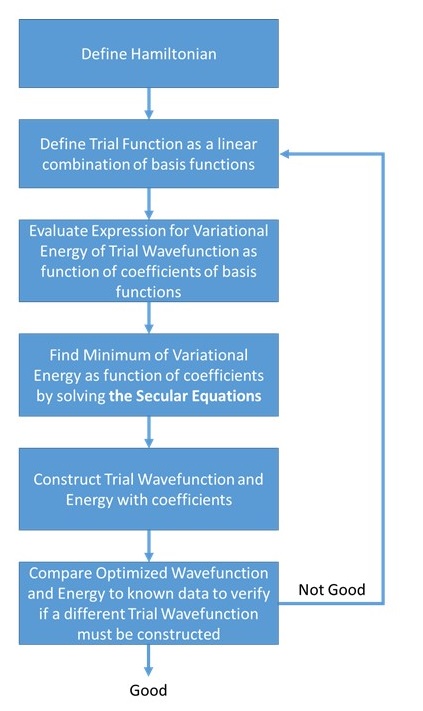
Los métodos variacionales, en particular el método variacional lineal, son las técnicas de aproximación más utilizadas en química cuántica. Para implementar tal método se necesita conocer al hamiltoniano\(H\) cuyos niveles de energía se buscan y se necesita construir una función de onda de prueba en la que exista cierta 'flexibilidad' (por ejemplo, como en el método variacional lineal donde los\(a_j\) coeficientes pueden ser variados). Esta herramienta se utilizará para desarrollar varios de los métodos orbitales moleculares más utilizados y potentes en química.
El Determinante Secular
A partir de las ecuaciones seculares con funciones ortonormales (Ecuación\ ref {seceq2}), tenemos ecuaciones seculares\(k\) simultáneas en\(k\) incógnitas. Estas ecuaciones también pueden escribirse en notación matricial, y para una solución no trivial (es decir,\(c_i \neq 0\) para todos\(i\)), el determinante de la matriz secular debe ser igual a cero.
\[ { | H_{ik}–ES_{ik}| = 0} \label{7.2.13} \]
- El determinante es un número real, no es una matriz.
- El determinante puede ser un número negativo.
- No se asocia en absoluto con el valor absoluto excepto que ambos usan líneas verticales.
- El determinante sólo existe para matrices cuadradas (\(2 \times 2\),\(3 \times 3\),...,\(n \times n\)). El determinante de una\(1 \times 1\) matriz es ese valor único en el determinante.
- La inversa de una matriz solo existirá si el determinante no es cero.
El determinante puede evaluarse mediante un método de expansión que involucra a menores y cofactores. Antes de que podamos usarlas, necesitamos definirlas. Es el producto de los elementos en la diagonal principal menos el producto de los elementos fuera de la diagonal principal. En el caso de una\(2 \times 2\) matriz, la fórmula específica para el determinante es
\[{\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.\end{aligned}}} \nonumber \]
Del mismo modo, supongamos que tenemos una\(3 \times 3\) matriz\(A\), y queremos la fórmula específica para su determinante\(|A|\):
\[{\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}} \nonumber \]
Para resolver la Ecuación\ ref {7.2.13}, el determinado debe expandirse y luego establecerse en cero. Eso genera un polinomio (llamado ecuación característica) que puede resolverse directamente con métodos de álgebra lineal o numéricamente.
Si\(|\psi_{trial} \rangle\) es una combinación lineal de dos funciones. En términos matemáticos,
\[|\psi_{trial} \rangle= \sum_{n=1}^{N=2} a_n |f_n\rangle = a_1 |\phi_1 \rangle + a_2 | \phi_2 \rangle \nonumber \]
entonces el determinante secular (Ecuación\(\ref{7.2.13}\)), en la formulación matricial se vería así
\[\begin{vmatrix} H_{11}-E_{trial}S_{11}&H_{12}-E_{trial}S_{12} \\ H_{12}-E_{trial}S_{12}&H_{22}-E_{trial}S_{22}\end{vmatrix}=0 \nonumber \]
Solución
Resolver las ecuaciones seculares se realiza encontrando\(E_{trial}\) y poniendo el valor en la expansión del determinante secular
\[a_1^2 H_{11} + 2a_1 a_2 H_{12}+ a_2^2 H_{22}=0 \nonumber \]
y
\[a_1(H_{12} - E_{trial}S_{12}) + a_2(H_{22} - E_{trial}S_{22}) = 0 \nonumber \]
La ecuación se\(\ref{7.2.13}\) puede resolver para obtener las energías\(E\). Cuando se disponen en orden de aumentar la energía, éstas proporcionan aproximaciones a las energías de los primeros\(k\) estados (cada uno teniendo una energía superior a la verdadera energía del estado en virtud del teorema de la variación). Para encontrar las energías de un mayor número de estados simplemente usamos un mayor número de funciones básicas\(\{\phi_i\}\) en la función de onda de prueba (Ejemplo\ ref {Ex1}). Para obtener la función de onda aproximada para un estado particular, sustituimos la energía apropiada en las ecuaciones seculares y resolvemos los coeficientes\(a_i\).
Mediante este método es posible encontrar todos los coeficientes\(a_1 \ldots a_k\) en términos de un coeficiente; normalizando la función de onda proporciona los valores absolutos para los coeficientes.
Funciones de onda de prueba que consisten en combinaciones lineales de funciones simples
\[ | \psi(r) \rangle = \sum_i a_i | \phi_i(r) \rangle \nonumber \]
forman la base del método de Combinación Lineal de Orbitales Atómicos (LCAO) introducido por Lennard y Jones y otros para calcular las energías y funciones de onda de átomos y moléculas. Las funciones\(\{| \phi_i \rangle \}\) se seleccionan para que los elementos de la matriz puedan ser evaluados analíticamente. Se pueden utilizar dos conjuntos básicos de funciones de orbitales atómicos: tipo Slater y tipo gaussiano:
Orbitales de Slater usando funciones de onda similares a hidrógeno
\[ | \phi_i \rangle = Y_{l}^{m}(\theta,\phi) e ^{-\alpha r} \nonumber \]
y orbitales gaussianos de la forma
\[ | \phi_i \rangle = Y_{l}^{m}(\theta,\phi) e ^{-\alpha r^2} \nonumber \]
son las formas más utilizadas, donde\(Y_l^m(\theta,\phi)\) están los armónicos esféricos que representan la parte angular de los orbitales atómicos. Los orbitales gaussianos forman la base de muchos códigos informáticos de química cuántica.
El método variacional lineal se utiliza ampliamente en orbitales moleculares de moléculas y otros ejemplos se pospondrán hasta esa discusión en los Capítulos 9.
Colaboradores y Atribuciones
Claire Vallance (University of Oxford)



Debido a que los orbitales de Slater dan resultados exactos para el Hidrógeno, utilizaremos orbitales gaussianos para probar el método LCAO en Hidrógeno, siguiendo a S.F. Boys, Proc. Roy. Soc. A 200, 542 (1950) y W.R. Ditchfield, W.J. Hehre y J.A. Pople, J. Chem. Phys. Rev. 52, 5001 (1970) con el conjunto de bases. Debido a que los productos de los gaussianos también son gaussianos, los elementos de la matriz requeridos se calculan fácilmente.