8.3: Las ecuaciones de Hartree-Fock se resuelven mediante el método de campo autoconsistente
- Page ID
- 79654
- Mostrar cómo se puede utilizar la aproximación de Hartree para resolver las funciones de onda y las energías de los átomos de múltiples electrones.
- Comprender el enfoque orbital de orbitales independientes es una aproximación a un sistema de electrones mutlti con los movimientos de todos los electrones acoplados entre sí.
- Demostrar cómo se necesita el cálculo del campo autoconsistente (SCF) para soportar la aproximación de Hartree
El método Hartree se utiliza para aproximar la función de onda y la energía de un sistema multielectrónico cuántico en estado estacionario. Esta aproximación supone que la función exacta\(N\) de onda del cuerpo del sistema puede ser aproximada por un producto de las funciones de onda de un solo electrón. Al invocar el método variacional, se puede derivar un conjunto de ecuaciones\(N\) acopladas para los N orbitales de espín. Una solución de estas ecuaciones produce la función de onda Hartree y la energía del sistema. Es un paso mejor que el enfoque de “La ignorancia es felicidad”, discutido anteriormente, pero aún lejos de los métodos modernos de vanguardia.
El sistema sin solución
El hamiltoniano para un átomo multielectrónico genérico incluye términos de atracción nucleo-electrón para los electrones adicionales con una carga general\(Z\); p.
\[V_{\text{nuclear-electron}}(r_1) = -\dfrac {Z}{\left\vert\mathbf{r} - \mathbf{R}\right\vert} \label{8.3.1} \]
en unidades atómicas con\(\left\vert\mathbf{r} - \mathbf{R}\right\vert\) es la distancia entre el electrón y el núcleo, El hamiltoniano también debe tener términos para la repulsión electrón-electrón (también en unidades atómicas)
\[V_{\text{electron-electron}}(r_{12}) = \dfrac {1}{\left\vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert} \label{8.3.2} \]
con\(\left\vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert\) es la distancia entre el electrón 1 y el electrón 2. Así que se puede construir el Hamiltoniano multielectrón apropiado
\[\hat {H} (r_1, r_2, ... r_n) = -\dfrac {\hbar ^2}{2m_e} \sum _i \nabla ^2_i + \sum _i V_{\text{nuclear-electron}} (r_i) + \sum _{i \ne j} V_{\text{electron-electron}} (r_{ij}) \label{8.3.3} \]
Dado lo que hemos aprendido de los sistemas mecánicos cuánticos anteriores que hemos estudiado, predecimos que las soluciones exactas a la ecuación de Schrödinger multielectrón consistirían en una familia de funciones de onda multi-electrón, cada una con un valor propio de energía asociado. Estas funciones de onda y energías describirían los estados terrestres y excitados del átomo de múltiples electrones, así como las ondas de hidrógeno y sus energías asociadas describen los estados terrestres y excitados del átomo de hidrógeno. También predeciríamos que los números cuánticos estarían involucrados.
El hecho de que los electrones interactúen a través de su repulsión electrón-electrón (término final en la Ecuación\(\ref{8.3.3}\)) significa que una función de onda exacta para un sistema multi-electrón sería una sola función que depende simultáneamente de las coordenadas de todos los electrones; es decir, un multi-electrón función de onda:
\[|\psi (r_1, r_2, \cdots r_i) \rangle \label{8.3.4} \]
Desafortunadamente, los términos de repulsión electrón-electrón hacen imposible encontrar una solución exacta a la ecuación de Schrödinger para muchos átomos de electrones.
La aproximación de Hartree
El método para encontrar las mejores funciones de onda de un electrón posibles que fue publicado por Douglas Hartree en 1948 y mejorado dos años después por Vladimir Fock. Para que la ecuación de Schrödinger sea analíticamente resoluble, las variables deben ser separables, las variables son las coordenadas de los electrones. Para separar las variables de una manera que retenga información sobre las interacciones electrón-electrón, se debe aproximar el término electrón-electrón (Ecuación\(\ref{8.3.1}\)) por lo que depende únicamente de las coordenadas de un electrón. Un hamiltoniano tan aproximado puede explicar la interacción de los electrones de una manera promedio. Las funciones propias exactas de un electrón de este hamiltoniano aproximado se pueden encontrar resolviendo la ecuación de Schrödinger. Estas funciones son las mejores funciones de un electrón posibles.
La aproximación de Hartree comienza invocando un ansatz inicial de que la función de onda multielectrónica en la ecuación se\(\ref{8.3.4}\) puede expandir como un producto de las funciones de onda de un solo electrón (es decir, orbitales)
\[ | \psi(\mathbf{r}_1,\mathbf{r}_2, \ldots, \mathbf{r}_N) \rangle \approx \psi_{1}(\mathbf{r}_1)\psi_{2}(\mathbf{r}_2) \ldots \psi_{N}(\mathbf{r}_N) \label{2.3} \]
de lo que se deduce que los electrones son independientes, e interactúan solo a través del potencial Coulomb del campo medio. Esto produce ecuaciones de Schrödinger de un electrón de la forma
\[-\dfrac{\hbar^{2}}{2m} \nabla^{2}\psi_{i}(\mathbf{r}) + V(\mathbf{r})\psi_{i}(\mathbf{r}) = \epsilon_{i}\psi_{i}(\mathbf{r}) \label{2.4} \]
o
\[H_e(r) \psi_{i}(\mathbf{r}) = \epsilon_{i}\psi_{i}(\mathbf{r}) \label{2.4B} \]
donde\(V(r)\) está el potencial en el que se mueve el electrón; esto incluye tanto la interacción nucleo-electrón
\[V_{nucleus}(\mathbf{r}) = -Ze^{2}\sum_{R} \dfrac{1}{\left\vert\mathbf{r} - \mathbf{R}\right\vert} \label{2.5} \]
y el campo medio que surge de los\(N-1\) otros electrones. Untamos los otros electrones en una densidad de carga negativa suave\(\rho(\mathbf{r}')\) que conduce a un potencial de la forma
\[V_{electron}(\mathbf{r}) = -e\int d\mathbf{r}^{\prime} \rho(\mathbf{r}^{\prime}) \dfrac{1}{\left\vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert} \label{2.6} \]
donde
\[\rho(\mathbf{r}) = \sum_{i}^{\text{occupied}}\vert\psi(\mathbf{r})\vert^{2}. \nonumber \]
La suma recorre todos los estados ocupados; es decir, sólo los estados de electrones que existen en el átomo. Las funciones de onda que desde este enfoque con el hamiltoniano\(H_e(r)\) implican poseen tres tipos de energías que se discuten a continuación.
La energía total\(\epsilon_j\) de la órbita\(\phi_j\), es la suma de las tres contribuciones anteriores:
- Energía cinética: La energía cinética del electrón tiene un valor promedio que se calcula tomando el valor esperado del operador de energía cinética\[\dfrac{- \hbar^2}{2m} \nabla^2 \nonumber \] con respecto a cualquier solución particular\(\phi_j(r)\) a la ecuación de Schrödinger:\[KE = \langle\phi_j| \dfrac{- \hbar^2}{2m} \nabla^2 |\phi_j\rangle \nonumber \]
- Energía de atracción coulómbica de electrones nucleares: Energía de atracción coulómbica con el núcleo de carga\(Z\):\[\langle\phi_j| \dfrac{-Z e^2}{\left\vert\mathbf{r} - \mathbf{R}\right\vert} |\phi_j\rangle \nonumber \]
- Energía de repulsión coulómbica de electrones: Energías de repulsión de Coulomb con todos los\(N-1\) demás electrones, que se supone que ocupan otros orbitales atómicos denotados\(\phi_K\), con esta energía calculada como\[\sum_{j\neq k} \langle\phi_j(r) \phi_k(r’) |\dfrac{e^2}{|r-r’|} | \phi_j(r) \phi_k(r’)\rangle.\label{8.3.8} \] La notación Dirac\(\langle\phi_j(r) \phi_k(r’) |\dfrac{e^2}{|r-r’|} | \phi_j(r) \phi_k(r’)\rangle\) se usa para representar los dos electrones ( seis-dimensional) Coulomb integral\[J_{j,k} = \int |\phi_j(r)|^2 |\phi_k(r’)|^2 \dfrac{e^2}{r-r'} dr dr’ \label{8.3.9} \] que describe la repulsión de Coulomb entre la densidad de carga\(|\phi_j(r)|^2\) para el electrón adentro\(\phi_j\) y la densidad de carga\(|\phi_k(r’)|^2\) para el electrón adentro\(\phi_k\). Por supuesto, la suma sobre\(k\) debe limitarse\(k=j\) a excluir para evitar contar una “autointeracción” del electrón en orbital\(\phi_j\) consigo mismo.
Sumando todos estos para obtener la energía total\(\epsilon_j\) de la órbita\(\phi_j\):
\[\epsilon_J = \langle\phi_j| \dfrac{- \hbar^2}{2m} \nabla^2 |\phi_j\rangle + \langle\phi_j| \dfrac{-Z e^2}{\left\vert\mathbf{r} - \mathbf{R}\right\vert} |\phi_j\rangle + \sum_{j\neq k} \langle\phi_j(r) \phi_k(r’) |\dfrac{e^2}{|r-r’|} | \phi_j(r) \phi_k(r’)\rangle.\label{8.3.10} \]
Este tratamiento de los electrones y sus orbitales se conoce como el nivel Hartree de la teoría.
Cuando se utilizan orbitales atómicos hidrogénicos cribados para aproximar los\(\phi_K\) orbitales\(\phi_j\) y, los\(\epsilon_J\) valores resultantes no producen predicciones precisas. Por ejemplo, el negativo de\(\epsilon_J\) debería aproximarse a la energía de ionización para la remoción de un electrón de los orbitales\(\phi_j\). Dichos potenciales de ionización (IP) se pueden medir, y los valores medidos no concuerdan bien con los valores teóricos cuando se realiza una aproximación de cribado crudo para los orbitales atómicos.
El enfoque de campo autoconsistente (SCF) para el método variacional
Las ecuaciones de Hartree son no lineales y deben resolverse iterativamente. Esto se debe a que si las partículas interactúan, esa interacción debe ser en el hamiltoniano. Entonces, hasta que sepamos dónde están las partículas, no podemos anotar al hamiltoniano, pero hasta que sepamos al hamiltoniano, no podemos decir dónde están las partículas.
La idea es resolver la ecuación de Schrödinger para un electrón que se mueve en el potencial del núcleo y de todos los demás electrones. Comenzamos con una suposición para la densidad de carga electrónica de prueba, resolvemos N/2 ecuaciones de Schrödinger de una partícula (inicialmente idénticas) para obtener funciones de onda de electrones N. Luego construimos el potencial para cada función de onda a partir del del núcleo y el de todos los demás electrones, lo simetrizamos y resolvemos de nuevo las ecuaciones N/2 de Schrödinger. Este método es ideal para una computadora, ya que se escribe fácilmente como un algoritmo (Figura 8.3.1 ).
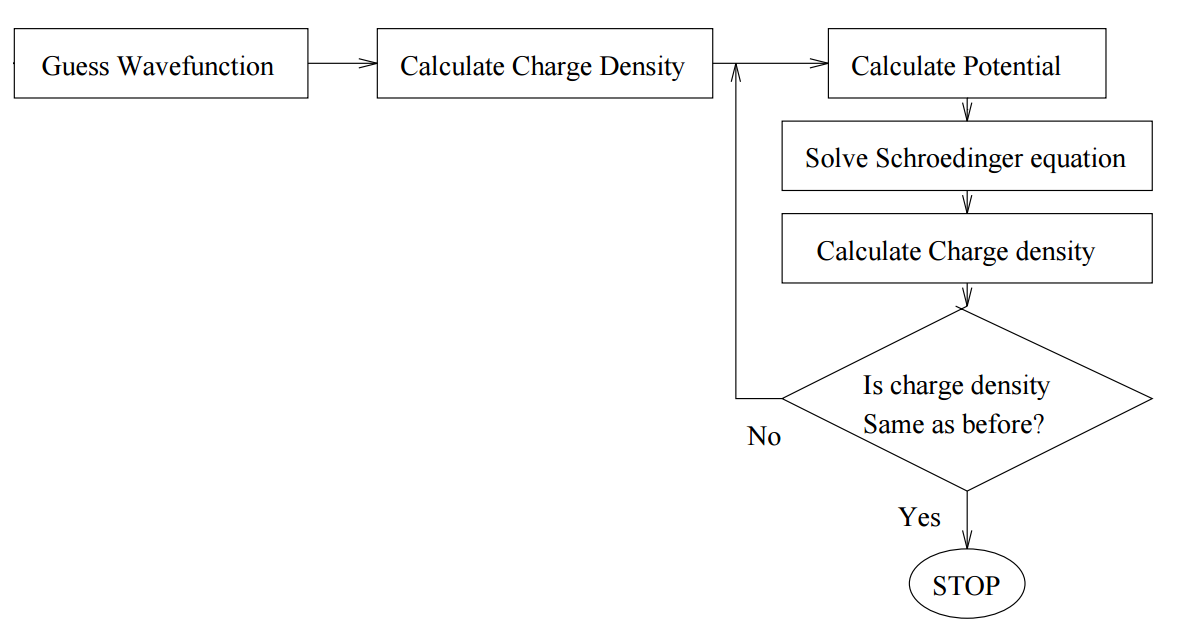
Aunque aquí nos preocupan los átomos, se emplea la misma metodología para moléculas o incluso sólidos (con simetrías potenciales apropiadas y condiciones límite). Este es un método variacional, por lo que dondequiera que nos referimos a las funciones de onda, asumimos que se expanden en algún conjunto de bases apropiado.
Fock mejoró el método de Hartree mediante el uso de “funciones de onda antisimétricas” adecuadas (llamadas el método Hartree-Fock) en lugar de simples funciones de onda de un electrón.
Los orbitales similares a hidrógeno proporcionan descripciones cualitativas de orbitales de átomos con más de un solo electrón. Al introducir el concepto de cribado como una forma de representar las interacciones repulsivas entre los electrones de un átomo, se\(Z_{\rm eff}\) puede utilizar una carga nuclear efectiva en lugar de\(Z\) en las\(E_{n,l}\) fórmulas hidrogénicas\(\psi_{n,l,m}\) y para generar orbitales atómicos aproximados para ser llenados por electrones en un átomo de muchos electrones. Por ejemplo, en la aproximación más cruda de un átomo de carbono, los dos\(1s\) electrones experimentan la atracción nuclear completa así\(Z_{\rm eff} =6\) para ellos, mientras que los\(2p\) electrones\(2s\) y son proyectados por los dos\(1s\) electrones, así\(Z_{\rm eff}= 4\) para ellos. Dentro de esta aproximación, uno ocupa entonces dos\(1s\) orbitales con\(Z=6\), dos\(2s\) orbitales con\(Z=4\) y dos\(2p\) orbitales con\(Z=4\) en la formación de la función de onda del producto de seis electrones completa del estado de carbono de menor energía
\[ | \psi(1, 2, …, 6) \rangle = | \psi_{1s}(1) \psi_{1s}(2) \psi_{2s}(3) \ldots \psi_{1p}(6) \rangle . \label{8.3.6} \]
Sin embargo, dichos orbitales aproximados no son suficientemente precisos para ser utilizados en simulaciones cuantitativas de estructura atómica y molecular. En particular, sus energías no siguen adecuadamente las tendencias en las energías orbitales atómicas (AO) que se enseñan en las clases introductorias de química (Figura 8.3.2 ).
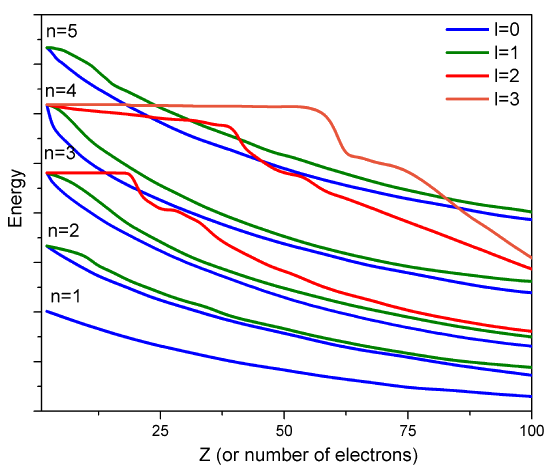
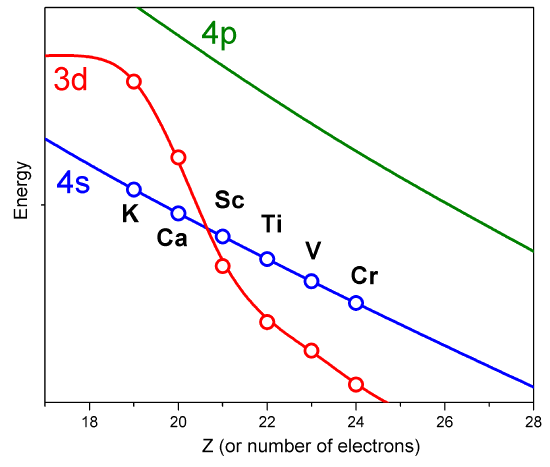
Por ejemplo, las energías relativas de los\(4s\) orbitales\(3d\) y no se describen adecuadamente en un modelo que trata los efectos de repulsión de electrones en términos de un simple factor de cribado. Entonces, ahora es el momento de examinar cómo podemos ir más allá del modelo de cribado y tomar en cuenta de una manera más confiable los efectos de repulsión de electrones, que provocan que los acoplamientos interelectrónicos que hacen que la ecuación de Schrödinger sea insoluble.
Colaboradores y Atribuciones
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Graeme Ackland (University of Edinburgh)

