12.2: Elementos de simetría
- Page ID
- 79737
Una operación de simetría es una acción que deja un objeto con el mismo aspecto después de que se haya realizado. Por ejemplo, si tomamos una molécula de agua y la giramos 180° alrededor de un eje que pasa por el átomo central de O (entre los dos átomos de H) se verá igual que antes. Cada operación de simetría tiene un elemento de simetría correspondiente, que es el eje, plano (bidimensional), línea (1-dimensional) o punto (0-dimensional) con respecto al cual se lleva a cabo la operación de simetría:

El elemento de simetría consiste en todos los puntos que permanecen en el mismo lugar cuando se realiza la operación de simetría. En una rotación, la línea de puntos que permanecen en el mismo lugar constituye un eje de simetría; en una reflexión los puntos que permanecen sin cambios conforman un plano de simetría. La simetría de una molécula o ion puede describirse en términos de la colección completa de operaciones de simetría que posee. Los elementos de simetría que una molécula (y cualquier otro objeto 3-D) puede poseer se discuten a continuación.
Una operación de simetría es una permutación de átomos tal que la molécula se transforma en un estado indistinguible del estado inicial.
Simetría de identidad,\(E\)
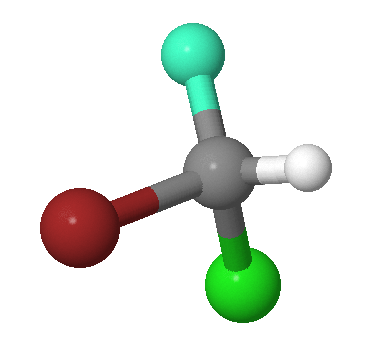
El operador de identidad,\(E\), consiste en no hacer nada, y el elemento de simetría correspondiente es la molécula entera. Cada molécula posee al menos esta operación. Por ejemplo, la\(\ce{CHFClBr}\) molécula en la Figura 12.2.1 . La operación de simetría de identificación no está indicada ya que todas las moléculas presentan esta simetría.
\(n\)-pliegue Eje de Rotación,\(C_n\)
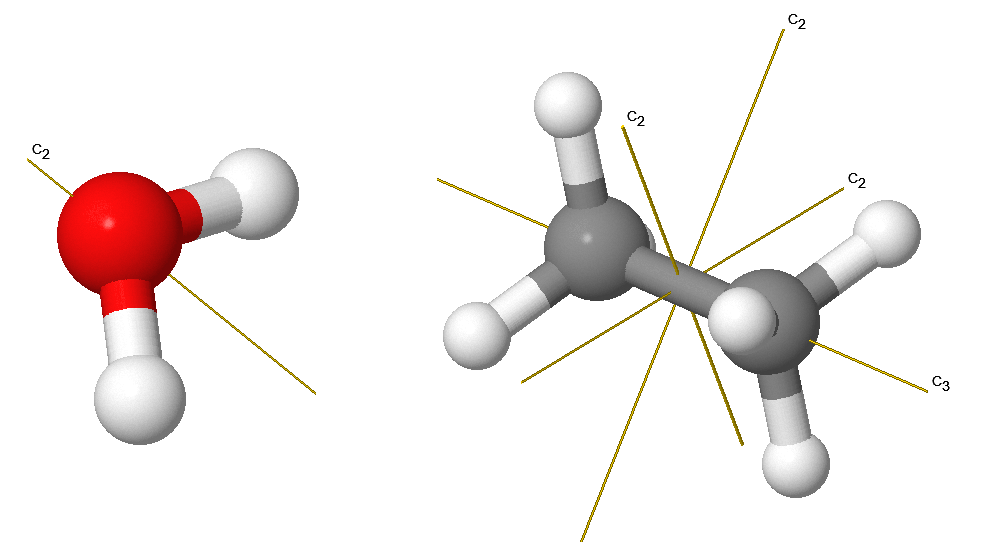
La operación de rotación (a veces llamada rotación adecuada)\(C_n\),, gira un objeto alrededor de un eje por\(2\pi/n\) radianes o\(360^{\circ}/n\). La rotación por\(C_n\) deja la molécula sin cambios. La\(H_2O\) molécula tiene un\(C_2\) eje (Figura 12.2.2 ). Las moléculas pueden tener más de un\(C_n\) eje, en cuyo caso la que tiene el mayor valor de\(n\) se denomina eje principal. En algunos sistemas de alta simetría, puede haber más de un eje principal. Tenga en cuenta que por convención, las rotaciones son en sentido antihorario alrededor del eje. \(C_n\)las rotaciones se indican a través de vectores con etiquetas como se indica a continuación.
Siempre queremos expresar rotaciones en sus fracciones equivalentes más simples de\(m/n\):
\[ C_4^2=C_2 \]
\[ C_6^4=C_3^2 \]
\[ C_8^6=C_4^3 \]
Girar un objeto\(n\) veces devuelve el objeto al objeto original y es equivalente a la operación de identidad,\(E\):
\[ C_n^n = E \nonumber \]
Las moléculas lineales tienen una simetría rotacional muy alta:\(C_\infty\). Los ejemplos incluyen diatomeas tales como\(\text{CO}\),\(\text{NO}\), y\(\text{CO}_2\).
Plano de simetría,\(\sigma\)
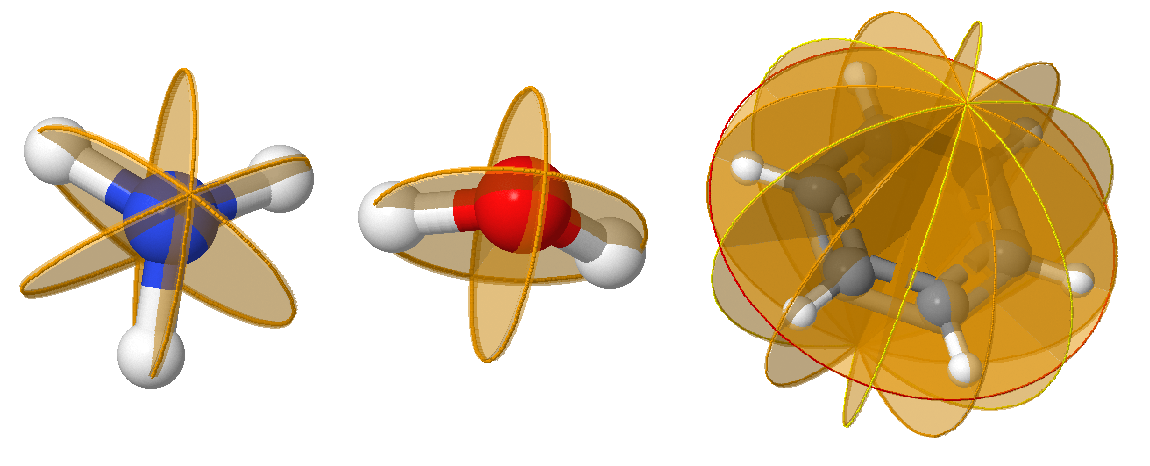
Reflexión,\(\sigma\), define la simetría bilateral alrededor de un plano (plano espejo/ plano de reflexión). La reflexión en el plano deja la molécula con el mismo aspecto. En una molécula que también tiene un eje de simetría, un plano espejo que incluye el eje se denomina plano espejo vertical y se etiqueta\(\sigma_v\), mientras que uno perpendicular al eje se denomina plano espejo horizontal y se etiqueta\(\sigma_h\). Un plano de espejo vertical que biseca el ángulo entre dos\(C_2\) ejes se denomina plano espejo diedro,\(\sigma_d\). Si no existe un eje principal,\(\sigma_h\) se define como el plano de la molécula. \(\sigma\)la simetría se indica como un plano sobre las moléculas; ya que a menudo bisectan átomos, lo que debe indicarse claramente.
Para cualquier plano de espejo, al realizar dos reflexiones sucesivas sobre el mismo plano, los objetos vuelven a su configuración original:
\[ \sigma\sigma=\sigma^2=E \nonumber \]
Centro de Simetría de Inversión,\(i\)
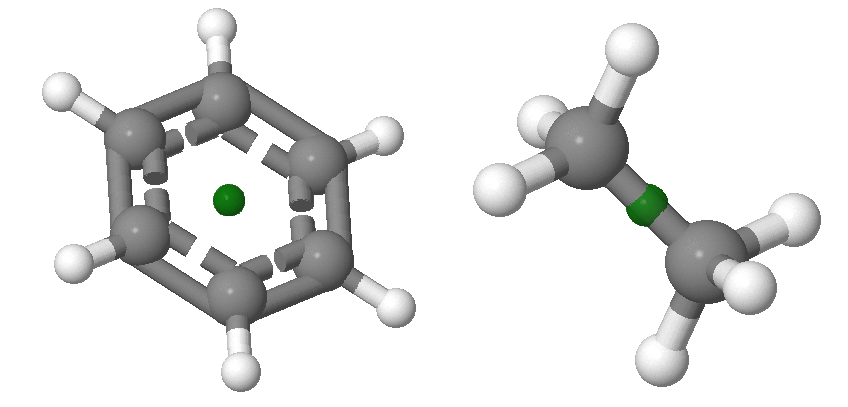
La inversión,\(i\), a través del centro de simetría deja la molécula sin cambios. La inversión consiste en pasar cada punto por el centro de inversión y salir a la misma distancia en el otro lado de la molécula. Si existe simetría de inversión, una línea dibujada desde cualquier átomo a través del centro se conectará con un átomo equivalente a una distancia equivalente del centro. Ejemplos de moléculas con centros de inversión se muestran en la Figura 12.2.4 . Los centros de inversión se indican a través de un punto, que puede o no solaparse con un átomo. El centro de inversión siempre está ubicado en el punto central de la molécula y solo puede haber un centro de inversión en cualquier sistema. Los centros de inversión en los ejemplos siguientes no se superponen con los átomos.
Realizar la inversión dos veces seguidas devuelve cada punto a su posición original:
\[ ii=i^2=E \nonumber \]
Se dice que las moléculas sin simetría de inversión son centrosimétricas.
\(n\)-doblar el eje de rotación incorrecta Simetría,\(S_n\)
Las rotaciones inadecuadas\(S_n\),, también se llaman rotación-reflexiones. La operación de rotación-reflexión consiste en girar\(C_n\) alrededor de un eje, seguido por la reflexión en un plano perpendicular al mismo eje. La simetría de rotación inadecuada se indica tanto con un eje como con un plano como se demuestra en los ejemplos de la Figura 12.2.5 .
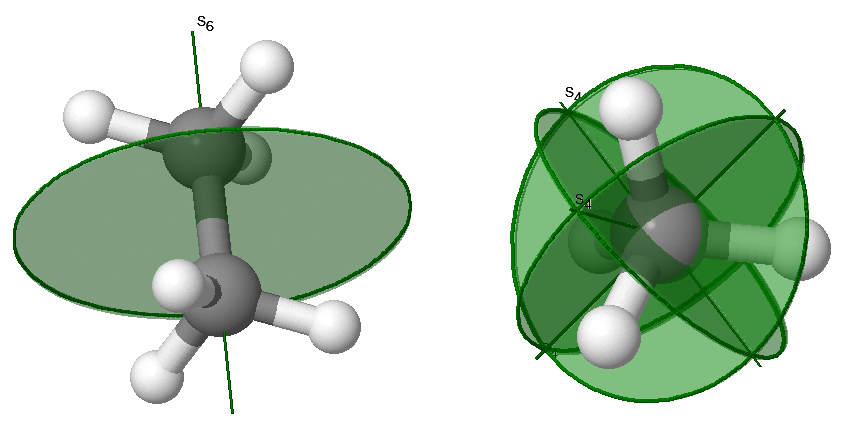
\(S_1\)es lo mismo que reflexión y\(S_2\) es lo mismo que inversión.
La rotación impropia de orden más bajo que no es una operación más sencilla es\(S_3\). El patrón de operaciones sucesivas depende de si\(n\) es par o impar. Las relaciones generales para\(S_n\) las operaciones son:
- Si\(n\) es par,\(S_n^n=E\)
- La molécula vuelve a la configuración de orientación original después de cada rotación completa
- Hay un número par de operadores de rotación y operadores de reflexión
- Si\(n\) es impar,\(S_n^n=\sigma\) y\(S_n^{2n}=E\)
- Primera rotación completa:
- Molecular no vuelve a la configuración original después de la primera rotación
- Hay un número impar de operadores de rotación y de reflexión
- Segunda rotación completa:
- La molécula vuelve a la configuración de orientación original
- Hay un número par de operadores de rotación y operadores de reflexión
- Primera rotación completa:
- Cuando\(m\) es par, siempre hay una rotación adecuada correspondiente (\(C_n\)):
- \(S_n^m=C_n^m\)cuando\(m<n\)
- \(S_n^m=C_n^{m-n}\)cuando\(m>n\) (2da rotación)
- Si\(S_n\) con incluso\(n\) existe,\(C_{n/2}\) existe
- Si\(S_n\) con impar\(n\) existe, entonces ambos\(C_n\) y\(\sigma\) perpendicular a\(C_n\) existir
Resumen de Symmetry Operations
La identidad\(E\) y las rotaciones\(C_n\) son operaciones de simetría que en realidad podrían llevarse a cabo sobre una molécula. Por esta razón se les llama operaciones de simetría adecuadas. Reflexiones, inversiones y rotaciones impropias sólo pueden imaginarse (en realidad no es posible convertir una molécula en su imagen especular o invertirla sin algún reordenamiento bastante drástico de los enlaces químicos) y como tales, se denominan operaciones de simetría inadecuadas. Estos cinco elementos de simetría se tabulan en la Tabla 12.2.1 con sus operadores correspondientes.
| Elementos de Símbolo | Descripción | Operador de Símbolo | Símbolo |
|---|---|---|---|
| \(E\) | identidad | \(\hat{E}\) | sin cambios |
| \(C_n\) | \(n\)-doblar el eje de rotación | \(\hat{C}_n\) | La rotación por\(360°/n\) deja la molécula sin cambios |
| \(\sigma\) | plano de simetría | \(\hat{\sigma}\) | La reflexión en el plano deja la molécula sin cambios |
| \(i\) | centro de simetría. | \(\hat{i}\) | La inversión a través del centro de simetría deja la molécula sin cambios. |
| \(S_n\) | \(n\)-doblar rotación inadecuada | \(\hat{S}_n\) | La operación de reflexión rotatoria consiste en rotar a través de un ángulo\(360°/n\) alrededor del eje, seguido de la reflexión en un plano perpendicular al eje. |
Definición del sistema de coordenadas
Convencionalmente, al imponer un conjunto de ejes cartesianos sobre una molécula (como tendremos que hacer más adelante en el curso), el\(z\) eje se encuentra a lo largo del eje principal de la molécula, el\(x\) eje se encuentra en el plano de la molécula (o en un plano que contiene el mayor número de átomos si la molécula es no plano), y el\(y\) eje constituye un sistema de eje diestro.
Generalmente, se observan las siguientes convenciones para definir el sistema de coordenadas:
- El origen del sistema de coordenadas se localiza en el átomo central o en el centro de la molécula.
- El\(z\) eje -es colineal con el eje rotacional de orden más alto (eje principal).
- Para moléculas planas, si el eje z es perpendicular al plano molecular:
- El\(x\) eje -se encuentra en el plano de la molécula y pasa por el mayor número de átomos.
- El\(x\) eje -se encuentra perpendicular al plano
- Para las moléculas no planas, una vez definido el eje z, el eje x es el usualmente elegido para que el plano xz contenga tantos átomos como sea posible.
Grupos de Puntos Moleculares
Solo es posible que ciertas combinaciones de elementos de simetría estén presentes en una molécula (o cualquier otro objeto). Como resultado, podemos agrupar moléculas que poseen los mismos elementos de simetría y clasificar las moléculas según su simetría. Estos grupos de elementos de simetría se denominan grupos de puntos (debido a que hay al menos un punto en el espacio que permanece sin cambios independientemente de qué operación de simetría del grupo se aplique). Existen dos sistemas de notación para etiquetar grupos de simetría, llamados los sistemas Schönflies y Hermann-Mauguin (o Internacional). La notación Schönflies es utilizada por químicos y espectroscopistas, mientras que los Cristógrafos prefieren la notación Hermann-Mauguin.La simetría de moléculas individuales generalmente se describe usando la notación Schö nflies, que se usa a continuación. Los grupos de puntos comunes se pueden clasificar en los siguientes:
- Grupos no rotacionales
- Grupos rotativos de un solo eje
- Grupos diedros
- Grupos cúbicos
Algunos de los grupos de puntos comparten sus nombres con operaciones de simetría, así que ten cuidado de no mezclarlos dos. Por lo general, queda claro a partir del contexto a cuál se está refiriendo a uno.
Grupos no rotacionales
Los grupos no rotacionales representan los grupos de simetría más bajos y tienen el orden más bajo (\(h=1,2\)). Los grupos no rotacionales incluyen:
- \(C_1\)- Contiene solo la identidad (una\(C_1\) rotación es una rotación de 360° y es lo mismo que la operación de identidad\(E\)). Las moléculas que pertenecen al\(C_1\) grupo no tienen simetría y por lo tanto son asimétricas. Un ejemplo es ChdfCl:
- \(C_i\)- Contiene la identidad\(E\) y un centro de inversión\(i\). Un ejemplo es C 2 H 2 F 2 Cl 2:
- \(C_S\)- Contiene la identidad\(E\) y un plano de reflexión\(\sigma\).
Grupos de rotación de un solo eje
Los grupos de rotación de un solo eje son ejemplos de grupos cíclicos. En grupos cíclicos, todos los operadores viajan (Abelian). En sus tablas de multiplicación, los elementos aparecen a lo largo de diagonales de derecha a izquierda. ¡Conocer este patrón facilita la construcción de tablas de multiplicación! Los grupos rotacionales de un solo eje incluyen:
- \(C_n\)- Contiene la identidad y un eje de rotación\(n\) -fold.
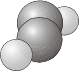
- \(C_{nv}\)- Contiene la identidad, un eje de rotación\(n\) -fold y planos de espejo\(n\) verticales\(\sigma_v\).
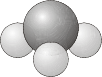

- \(C_{nh}\)- Contiene la identidad, un eje de rotación\(n\) -fold y un plano de reflexión horizontal \(\sigma_h\)(tenga en cuenta que en\(C_{2h}\) esta combinación de elementos de simetría implica automáticamente un centro de inversión).
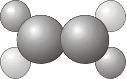
- \(S_n\)- Contiene la identidad y un\(S_n\) eje. Obsérvese que las moléculas solo pertenecen\(S_n\) si no se han clasificado ya en términos de uno de los grupos puntuales precedentes (por ejemplo,\(S_2\) es el mismo que\(C_i\), y una molécula con esta simetría ya habría sido clasificada).
Grupos diedros
Los grupos diedros tienen ejes\(n\) dobles perpendiculares al eje principal\(n\) de pliegue. Estos\(C_2\) ejes se denominan ejes diedros. Los grupos diedros incluyen:
- \(D_n\)- Contiene la identidad, un eje de rotación\(n\) -fold y rotaciones de\(n\) 2 veces alrededor de ejes perpendiculares al eje principal.

- \(D_{nh}\)- Contiene los mismos elementos de simetría que\(D_n\) con la adición de un plano de espejo horizontal.

- \(D_{nd}\)- Contiene los mismos elementos de simetría que\(D_n\) con la adición de planos de espejo\(n\) diedro.
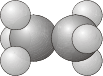
Grupos cúbicos
Los siguientes grupos son los grupos cúbicos, los cuales contienen más de un eje principal. Los grupos cúbicos están asociados con poliedros que están geométricamente relacionados con el cubo. Todos se caracterizan por la presencia de múltiples ejes rotacionales intersecantes de orden superior. Se separan en los grupos tetraédricos (\(T_d\),\(T_h\) y\(T\)) y los grupos octaédricos (\(O\)y\(O_h\)). El grupo icosaédrico también existe, pero no se incluye a continuación.
- \(T_d\)- Contiene todos los elementos de simetría de un tetraedro regular, incluyendo la identidad, 4\(C_3\) ejes, 3\(C_2\) ejes, 6 planos de espejo diedro y 3\(S_4\) ejes e.g\(\ce{CH_4}\).
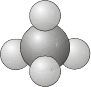
- \(T\)- Igual que para\(T_d\) pero sin planos de reflexión.
- \(T_h\)- Igual que para\(T\) pero contiene un centro de inversión.
- \(O_h\)- El grupo del octaedro regular e.g\(\ce{SF_6}\).
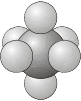
- \(O\)- Igual que para\(O_h\), pero sin planos de reflexión.
Resumen de grupos
El grupo final es el grupo de rotación completa\(R_3\), que consiste en un número infinito de\(C_n\) ejes con todos los valores posibles de\(n\) y describe la simetría de una esfera. Los átomos (pero ninguna molécula) pertenecen a\(R_3\), y el grupo tiene importantes aplicaciones en la mecánica cuántica atómica. Sin embargo, aquí no vamos a tratarlo más.
| Grupos no axiales | C 1 | C s | C i | - | - | - | - | - | - |
|---|---|---|---|---|---|---|---|---|---|
| C n grupos | C 2 | C 3 | C 4 | C 5 | C 6 | C 7 | C 8 | - | - |
| D n grupos | D 2 | D 3 | D 4 | D 5 | D 6 | D 7 | D 8 | - | - |
| Grupos C nv | C 2v | C 3v | C 4v | C 5v | C 6v | C 7v | C 8v | - | - |
| C nh grupos | C 2h | C 3h | C 4h | C 5h | C 6h | - | - | - | - |
| Grupos D nh | D 2h | D 3h | D 4h | D 5h | D 6h | D 7h | D 8h | - | - |
| Grupos D nd | D 2d | D 3d | D 4d | D 5d | D 6d | D 7d | D 8d | - | - |
| S n grupos | S 2 | - | S 4 | - | S 6 | S 8 | S 10 | S 12 | |
| Grupos cúbicos | T | T h | T d | O | O h | I | I h | - | - |
| Grupos lineales | C ∞ v | D ∞ h | - | - | - | - | - | - | - |
Una vez que se familiarice con los elementos de simetría y los grupos de puntos descritos anteriormente, le resultará bastante sencillo clasificar una molécula en términos de su grupo de puntos. Mientras tanto, el diagrama de flujo que se muestra a continuación proporciona un enfoque paso a paso del problema.
1 Aunque el sistema Hermann-Mauguin puede usarse para etiquetar grupos de puntos, generalmente se usa en la discusión de la simetría cristalina. En los cristales, además de los elementos de simetría descritos anteriormente, los elementos de simetría traslacional son muy importantes. Las operaciones de simetría traslacional no dejan ningún punto sin cambios, con la consecuencia de que la simetría cristalina se describe en términos de grupos espaciales en lugar de grupos de puntos
Simetría y propiedades físicas
Realizar una operación de simetría sobre una molécula no debe cambiar ninguna de sus propiedades físicas. Resulta que esto tiene algunas consecuencias interesantes, lo que nos permite predecir si una molécula puede ser quiral o polar sobre la base de su grupo puntual.
Para que una molécula tenga un momento dipolar permanente, debe tener una distribución de carga asimétrica. El grupo puntual de la molécula no solo determina si la molécula puede tener un momento dipolar, sino también en qué dirección puede apuntar. Si una molécula tiene un\(C_n\) eje con\(n > 1\), no puede tener un momento dipolar perpendicular al eje de rotación (por ejemplo, una\(C_2\) rotación cambiaría los extremos de dicho momento dipolar e invertiría la polaridad, lo cual no está permitido — rotaciones con valores más altos de \(n\)también cambiaría la dirección en la que apunta el dipolo). Cualquier dipolo debe quedar paralelo a un\(C_n\) eje.
Además, si el grupo puntual de la molécula contiene alguna operación de simetría que pueda intercambiar los dos extremos de la molécula, como un plano\(\sigma_h\) espejo o una\(C_2\) rotación perpendicular al eje principal, entonces no puede haber un momento dipolar a lo largo del eje. Los únicos grupos compatibles con un momento dipolo son\(C_n\),\(C_{nv}\) y\(C_s\). En las moléculas que pertenecen a\(C_n\) o\(C_{nv}\) el dipolo deben estar a lo largo del eje de rotación.
Un ejemplo de simetría en química que ya habrás encontrado se encuentra en los pares isoméricos de moléculas llamadas enantiómeros. Los enantiómeros son imágenes especulares no superponibles entre sí, y una consecuencia de esta relación simétrica es que giran el plano de luz polarizada que pasa a través de ellos en direcciones opuestas. Se dice que tales moléculas son quirales, 2 lo que significa que no pueden superponerse a su imagen especular. Formalmente, el elemento de simetría que impide que una molécula sea quiral es un eje de rotación-reflexión\(S_n\). Tal eje suele estar implícito por otros elementos de simetría presentes en un grupo.
Por ejemplo, un grupo de puntos que tenga\(C_n\) y\(\sigma_h\) como elementos también tendrá\(S_n\). De igual manera, un centro de inversión es equivalente a\(S_2\). Como regla general, una molécula definitivamente no puede tener ser quiral si tiene un centro de inversión o un plano espejo de cualquier tipo (\(\sigma_h\),\(\sigma_v\) o\(\sigma_d\)), pero si estos elementos de simetría están ausentes la molécula debe ser revisada cuidadosamente para un\(S_n\) eje antes de ella se supone que es quiral.
La palabra quiral tiene su origen en la palabra griega para mano (\(\chi\)\(\epsilon\)\(\rho\)\(\iota\), pronunciada 'cheri' con un ch suave como en 'loch'). Un par de manos también es un par de imágenes especulares no superponibles, y a menudo escucharás quiralidad referida como 'mano' por esta razón.
Resumen
Todas las moléculas pueden describirse en términos de su simetría o falta de la misma, la cual puede contener elementos de simetría (punto, línea, plano). La reflexión, rotación e inversión son operaciones de simetría (movimiento de las moléculas de tal manera que después del movimiento, todos los átomos de las moléculas es coincidente con el átomo equivalente de la molécula en el original).


