13.2: Rotaciones Acompañan Transiciones Vibracionales

Cada uno de los modos de vibración de las moléculas diatómicas en la fase gaseosa también contiene estados de energía muy espaciados (diferencia de 1-10 cm ^-1) atribuibles a las transiciones rotacionales que acompañan a las transiciones vibracionales. La rotación de una molécula puede verse afectada por su transición vibracional porque hay un cambio en la longitud del enlace, por lo que se espera que ocurran estas transiciones rotacionales. Dado que los estados de energía vibracional son del orden de 1000 cm ^-1, los estados de energía rotacional pueden superponerse a los estados de energía vibratoria.

Reglas de selección

Las transiciones rotacionales y de vibración (también conocidas como rotor rígido y oscilador armónico) de las moléculas nos ayudan a identificar cómo interactúan las moléculas entre sí, su longitud de enlace como se mencionó en la sección anterior. Para conocer cada transición, hay que considerar otros términos como número de onda, constante de fuerza, número cuántico, etc. Hay niveles de energía rotacional asociados a todos los niveles vibracionales. A partir de esto, las transiciones vibracionales se pueden acoplar con transiciones rotacionales para dar espectros rovibracionales. Los espectros rovibracionales se pueden analizar para determinar la longitud promedio del enlace.

Tratamos las vibraciones de la molécula como las de un oscilador armónico (ignorando la anharmonía). La energía de una vibración es cuantificada en niveles discretos y dada por

\[E_v=h\nu \left(v+\dfrac{1}{2} \right) \nonumber \]

Donde v es el número cuántico vibracional y puede tener valores enteros 0, 1, 2..., y\(\nu\) is the frequency of the vibration given by:

\[\nu=\dfrac{1}{2\pi}\left(\dfrac{k}{\mu}\right)^\dfrac{1}{2} \nonumber \]

donde\(k\) es la constante de fuerza y\(\mu\) es la masa reducida de una molécula diatómica con masas atómicas\(m_1\) y\(m_2\), dada por

\[\mu=\dfrac{{m}_1{m}_2}{{m}_1+{m}_2} \label{reduced mass} \]

Tratamos las rotaciones de la molécula como las de un rotor rígido (ignorando la distorsión centrífuga desde aspectos no rígidos del rotor). La energía de una rotación también se cuantifica en niveles discretos dados por

\[ E_r=\dfrac{h^2}{8\pi^2I} J(J+1) \nonumber \]

En el que\(I\) se encuentra el momento de inercia, dado por

\[{I}=\mu{r}^2 \nonumber \]

donde\(\mu\) está la masa reducida (Ecuación\ ref {masa reducida}) y\(r\) es la longitud del enlace de equilibrio.

Experimentalmente, las frecuencias o números de onda se miden en lugar de energías, y dividiendo\(h\) o\(hc\) dando símbolos de término más comúnmente vistos,\(F(J)\) usando el número cuántico rotacional\(J\) y la constante de rotación\(B\) en cualquiera de las frecuencias

\[F(J)=\dfrac{E_r}{h}=\dfrac{h}{8\pi^2I} J(J+1)=BJ(J+1) \nonumber \]

o números de onda

\[\tilde{F}(J)=\dfrac{E_r}{hc}=\dfrac{h}{8\pi^2cI} J(J+1)=\tilde{B}J(J+1) \nonumber \]

Es importante señalar en qué unidades se está trabajando ya que la constante rotacional siempre se representa como\(B\), ya sea en frecuencia o en números de onda.

• Reglas de Selección de Transición Vibracional: A temperatura ambiente, normalmente solo se llena el estado vibracional de energía más baja v= 0, por lo que normalmente v ₀ = 0 y ∆v = +1. La regla de selección completa es técnicamente que ∆v = ±1, sin embargo aquí asumimos que la energía solo puede ir hacia arriba debido a la falta de población en los estados vibracionales superiores.
• Reglas de selección de transición rotacional: A temperatura ambiente, los estados con J≠ 0 se pueden poblar ya que representan la estructura fina de los estados vibracionales y tienen diferencias de energía menores que los sucesivos niveles vibracionales. Adicionalmente, ∆J = ±1 ya que un fotón contiene un cuántico de momento angular y cumplimos con el principio de conservación de energía. Esta es también la regla de selección para las transiciones rotacionales.

Estas dos reglas de selección significan que la transición ∆J = 0 (es decir, J” = 0 y J' = 0, pero\(\nu_0 \neq 0\) is forbidden and the pure vibrational transition is not observed in most cases. The rotational selection rule gives rise to an R-branch (when ∆J = +1) y una rama P (cuando ∆J = -1). Cada línea de la rama se etiqueta R (J) o P (J), donde J representa el valor del estado inferior Figura 13.2.1 ).

Figura 13.2.1 : Transiciones Rotación-Vibración. Las transiciones rotacionales son del orden de 1-10 cm ^-1, mientras que las transiciones vibracionales son del orden de 1000 cm ^-1. La diferencia de magnitud entre las transiciones de energía permite que los niveles rotacionales se superpongan dentro de los niveles vibracionales.

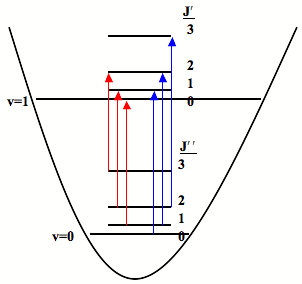
Rama R

Cuando ∆J = +1, es decir, el número cuántico rotacional en el estado fundamental es uno más que el número cuántico rotacional en el estado excitado — rama R (en francés, rico o rico). Para encontrar la energía de una línea de la rama R:

\[\begin{align} \Delta{E} &=h\nu_0 +hB \left [J(J+1)-J^\prime (J^\prime{+1}) \right] \\[4pt] &=h\nu_0 +hB \left[(J+1)(J+2)-J(J+1)\right] \\[4pt] &= h\nu_0 +2hB(J+1) \end{align} \nonumber \]

Sucursal P

Cuando ∆J = -1, es decir, el número cuántico rotacional en el estado fundamental es uno menor que el número cuántico rotacional en el estado excitado — rama P (en francés, pauvre o pobre). Para encontrar la energía de una línea de la rama P:

\[\begin{align} \Delta{E} &=h\nu_0 +hB \left [J(J+1)-J^\prime(J^\prime+1) \right] \\[4pt] &= h\nu_0 +hB \left [J(J-1)-J(J+1) \right] \\[4pt] &= h\nu_0 -2hBJ \end{align} \nonumber \]

Sucursal Q

Cuando ∆J = 0, es decir, el número cuántico rotacional en el estado fundamental es el mismo que el número cuántico rotacional en el estado excitado — rama Q (simple, la letra entre P y R). Para encontrar la energía de una línea de la rama Q:

\[ \begin{align} \Delta{E} &=h\nu_0 +hB[J(J+1)-J^\prime(J^\prime+1)] \\[4pt] &=h\nu_0 \end{align} \nonumber \]

La rama Q se puede observar en moléculas poliatómicas y moléculas diatómicas con momento angular electrónico en estado electrónico básico, por ejemplo, óxido nítrico, NO. La mayoría de las diatómicas, como el O ₂, tienen un pequeño momento de inercia y, por lo tanto, un momento angular muy pequeño y no producen rama Q.

Figura 13.2.3 : Representación de dibujos animados de los niveles de energía rotacional, J, impuestos a los niveles de energía vibracional, v. Las transiciones entre niveles que resultarían en las ramas P y R se representan en púrpura y rojo, respectivamente, además de la línea teórica de rama Q en azul.

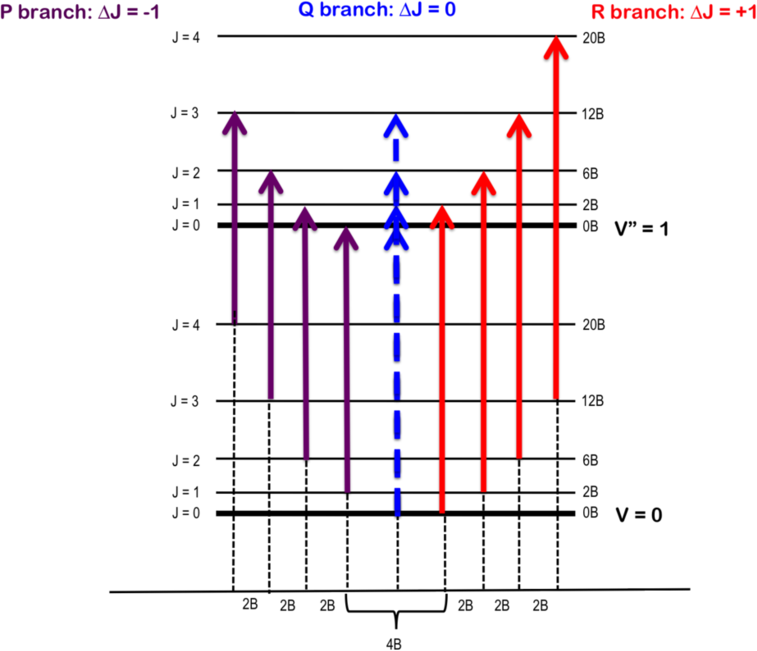
Como se ve en la Figura 13.2.2 , las líneas de la rama P (representada por flechas moradas) y la rama R (representada por flechas rojas) están separadas por múltiplos específicos de\(B\) (es decir,\(2B\)), por lo que la longitud del enlace se puede deducir sin necesidad de espectroscopía rotacional pura.

La energía nuclear total de los términos combinados de rotación-vibración,\(S(v, J)\), se puede escribir como la suma de la energía vibratoria y la energía rotacional

\[ S(v,J)=G(v)+F(J) \nonumber \]

donde\(G(v)\) representa la energía del oscilador armónico, ignorando los componentes anarmónicos y\(S(J)\) represents the energy of a rigid rotor, ignoring centrifugal distortion.

De esto, podemos derivar

\[ S(v,J)=\nu_0 \left(v+\dfrac{1}{2}\right) +BJ(J+1) \nonumber \]

El espectro que esperamos, basado en las condiciones descritas anteriormente, consiste en líneas equidistantes en energía entre sí, separadas por un valor de\(2B\). La intensidad relativa de las líneas es función de las poblaciones rotacionales de los estados terrestres, es decir, la intensidad es proporcional al número de moléculas que han realizado la transición. La intensidad general de las líneas depende del momento dipolar de transición vibracional.

Figura 13.2.3 : Una representación caricatura de un espectro rovibracional ideal.

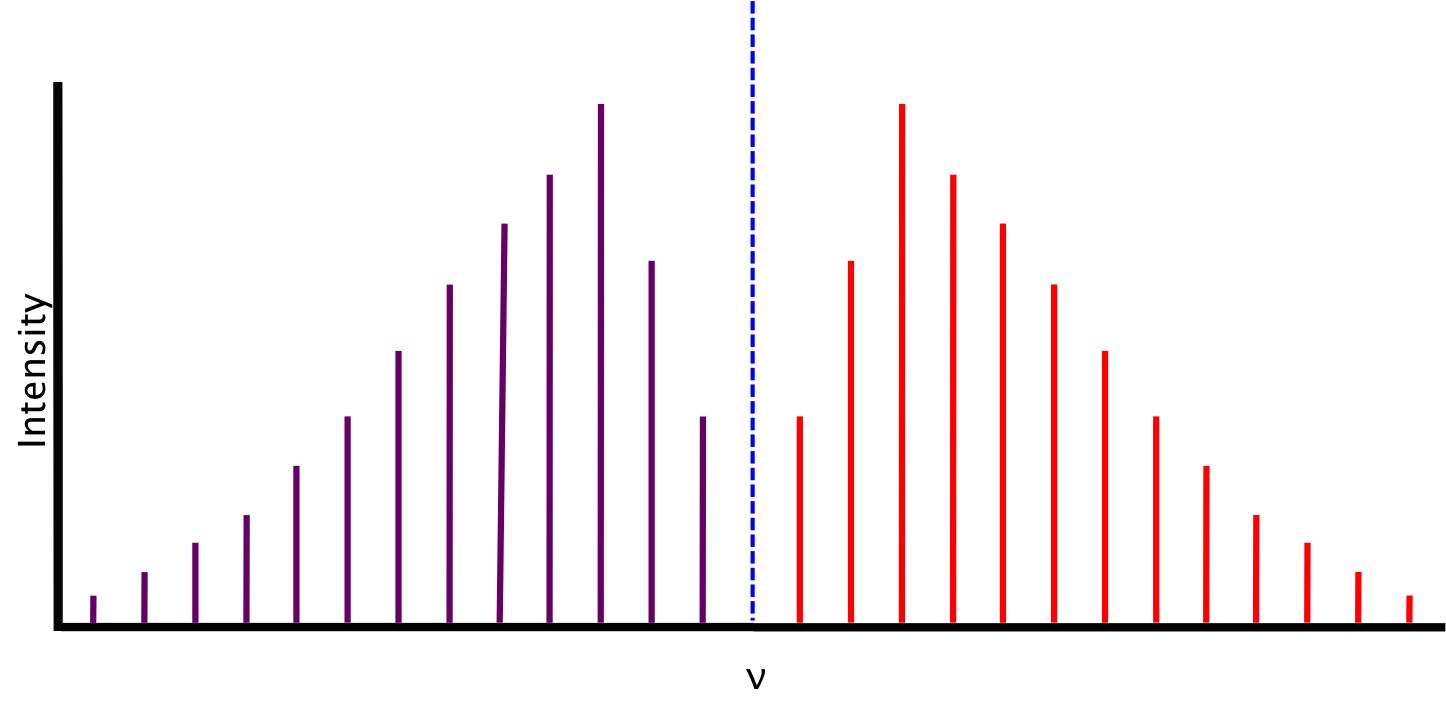
En la Figura 13.2.2 , entre\(P(1)\) y\(R(0)\) yace el hueco cero, donde las primeras líneas de la rama P- y R están separadas por\(4B\), asumiendo que la constante rotacional B es igual para ambos niveles de energía. El hueco cero es también donde esperaríamos la rama Q, representada como la línea punteada, si se permite.

Concepto Avanzado: Ocupaciones (Intensidades de Pico)

La intensidad relativa de las líneas ramificadas P y R depende de la distribución térmica de los electrones; más específicamente, dependen de la población del estado J inferior. Si representamos la población del nivel superior Jth como N _J y la población del estado inferior como N ₀, podemos encontrar la población del estado superior en relación con el estado inferior utilizando la distribución de Boltzmann:

\[\dfrac{N_J}{N_0}={(2J+1)e}^\left(-\dfrac{E_r}{kT}\right) \nonumber \]

(2J+1) da la degeneración del nivel superior Jth derivada de los valores permitidos de M _J (+J a —J). A medida que J aumenta, el factor de degeneración aumenta y el factor exponencial disminuye hasta que a J alto, el factor exponencial gana y N _J /N ₀ se acerca a cero en cierto nivel, J _máx. Así, cuando

\[ \dfrac{d}{dJ} \left( \dfrac{N_J}{N_0} \right)=0 \nonumber \]

por diferenciación, obtenemos

\[J_{max}=\left(\dfrac{kT}{2hB}\right)^\dfrac{1}{2}-\dfrac{1}{2} \nonumber \]

Esta es la razón por la que las líneas espectrales rovibracionales aumentan en energía hasta un máximo a medida que J aumenta, luego disminuyen a cero a medida que J continúa aumentando, como se ve en la Figura 13.2.2 .

De esta relación, también podemos deducir que en las moléculas más pesadas,\(B\) disminuirá porque el momento de inercia aumentará, y la disminución en el factor exponencial es menos pronunciada. Esto da como resultado que la distribución poblacional cambie a valores más altos de J. De igual manera, a medida que aumente la temperatura, la distribución poblacional se desplazará hacia valores más altos de\(J\)