13.5: Tonos vibracionales

Aunque el oscilador armónico resulta útil a niveles de energía más bajos, como\(v=1\), falla en números más altos de\(v\), fallando no solo en modelar adecuadamente los enlaces y disociaciones atómicos, sino que también es incapaz de igualar los espectros que muestran líneas adicionales de las que se cuenta en el modelo de oscilador armónico.

Anarmonicidad

Hasta este punto, hemos estado utilizando el oscilador armónico para describir la energía potencial internuclear del movimiento vibracional. Frecuencias vibracionales fundamentales de una molécula corresponde a la transición de\(\Delta v= \pm 1\). Si bien esta es una aproximación decente, los bonos no se comportan como lo hacen en la aproximación del Oscilador Armónico (Figura 13.5.1 ). Para ejemplo, a diferencia de la parábola dada en la aproximación del Oscilador Armónico, los átomos que están demasiado separados se disociarán.

Figura 13.5.1 : En la imagen de arriba se muestra la aproximación del oscilador armónico (parábola verde) superpuesta sobre el oscilador anarmónico (curva azul) en un diagrama de energía potencial. V (R) es la energía potencial de una molécula diatómica y R es el radio entre los centros de los dos átomos. Hacia la izquierda está la compresión del enlace, hacia la derecha es la extensión. (CC BY-SA 3.0; Creado por Mark Somoza 26 de marzo de 2006).

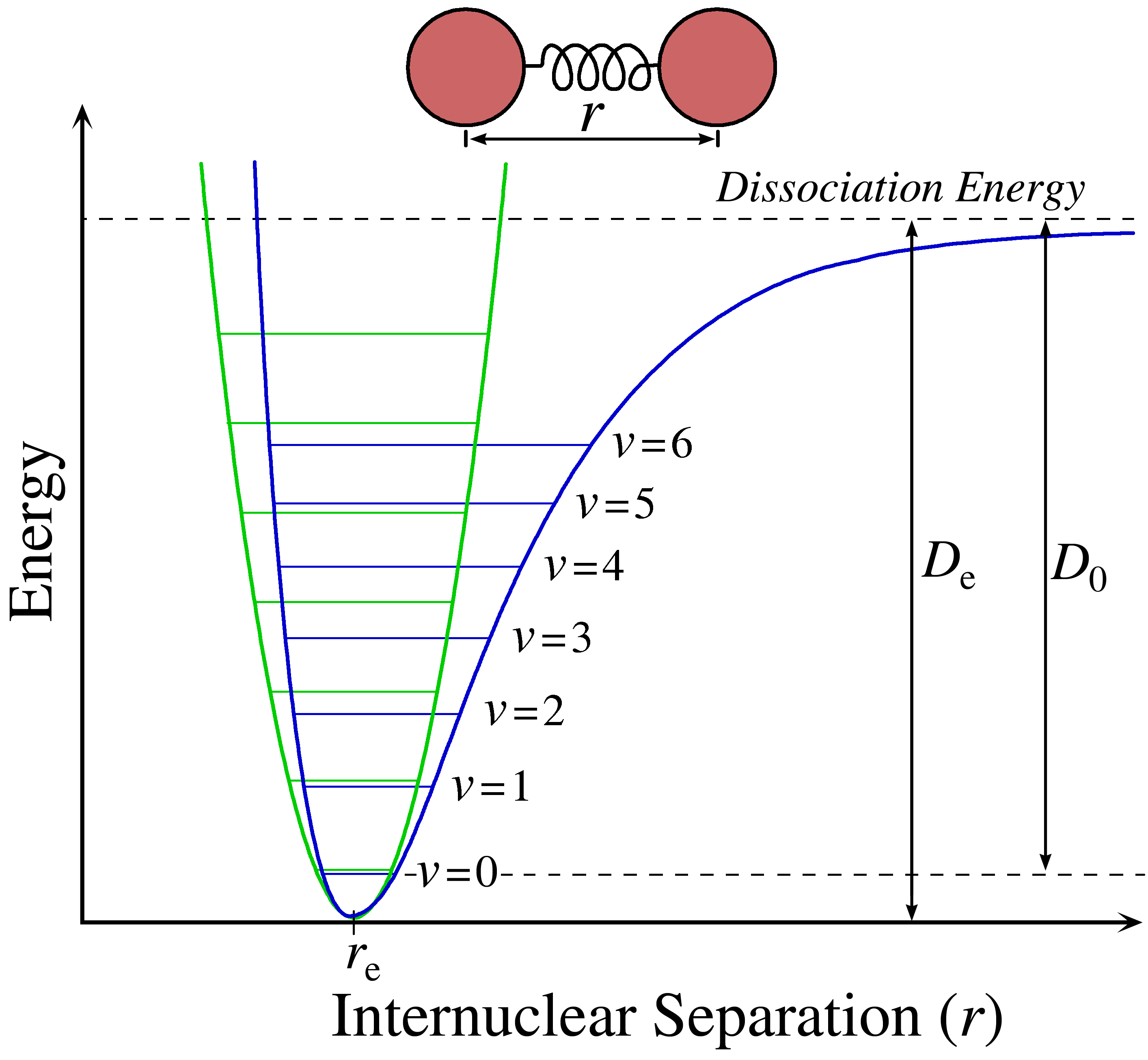
Como puede ver en la Figura 13.5.1 , el potencial del oscilador armónico (en verde) bien solo se ajusta aproximadamente sobre el pozo del oscilador anarmónico más preciso (en azul). La línea continua da cuenta de la disociación a valores R grandes, que las líneas punteadas ni siquiera cubren remotamente. Sin embargo, esta es solo una diferencia importante entre los osciladores armónicos y anarmónicos (reales).

La energía potencial real se puede ampliar en la serie Taylor.

\[ V(R) = V(R_e) + \dfrac{1}{2!}\left(\dfrac{d^2V}{dR^2}\right)_{R=R_e} (R-R_e)^2 + \dfrac{1}{3!}\left(\dfrac{d^3V}{dR^3}\right)_{R=R_e} (R-R_e)^3 + \dfrac{1}{4!}\left(\dfrac{d^4V}{dR^4}\right)_{R=R_e} (R-R_e)^4 + ... \label{taylor} \]

Esta expansión se discutió en detalle previamente. El primer término en la expansión se ignora ya que la derivada del potencial at\(R_e\) es cero (es decir, en el fondo del pozo). La aproximación del oscilador armónico solo usa el siguiente término, el término cuadrático, en la serie

\[V_{HO}(R) \approx V(R_e) + \dfrac{1}{2!}\left(\dfrac{d^2V}{dR^2}\right)_{R=R_e} (R-R_e)^2 \nonumber \]

o en términos de una constante de resorte (e ignorar el término de energía absoluta) y definir\(r\) para igualar el desplazamiento del equilibrio (\(r=R-R_e\)), entonces obtenemos el potencial oscilador armónico “estándar”:

\[V_{HO}(R) = \dfrac {1}{2} kr^2 \nonumber \]

Alternativamente, la expansión en la ecuación se\(\ref{taylor}\) puede acortar al término cúbico

\[V(x) = \dfrac {1}{2} kr^2 + \dfrac {1}{6} \gamma r^3 \label{cubic} \]

donde

• \(V(x_0) = 0\), y\(r = R - R_0\).
• \(k\)es la constante de la fuerza armónica, y
• \(\gamma\)es el primer término anarmónico (es decir, cúbico)

Es importante señalar que esta aproximación sólo es buena para\(R\) cerca\(R_0\).

Figura 13.5.2 : (izquierda) Desviación de aproximación simple del potencial armónico (curva roja) del potencial verdadero/exacto (curva azul) con término cúbico (verde). (derecha) Expansión con términos cuárticos positivos o negativos. (CC BY-NC; Ümit Kaya vía LibreTexts)

La aproximación del oscilador armónico y da por las siguientes energías:

\[ E_{v} = \tilde{\nu} \left (v + \dfrac{1}{2} \right) \nonumber \]

Cuando se incluyen términos cúbicos en la expansión (Ecuación\(\ref{cubic}\)), entonces la ecuación de Schrödinger resuelta, usando la teoría de la perturbación, da:

\[  E_{v} = \tilde{\nu} \left (v + \dfrac{1}{2} \right) - \tilde{\chi_e} \tilde{\nu} \left (v + \dfrac{1}{2} \right)^2 \nonumber \]

donde\( \tilde{\chi_e}\) está la constante de anarmonicidad. Es mucho menor que 1, lo que tiene sentido porque los términos de la serie Taylor se acercan a cero. Es por ello que, aunque\(G(n)\) técnicamente incluye toda la serie Taylor, sólo nos preocupamos por el primer y segundo términos. El resto son tan pequeños y apenas se suman al total y así pueden ser ignorados. Para obtener una aproximación más precisa, se pueden incluir más términos, pero de lo contrario, se pueden ignorar. Casi todas las diatómicas han determinado\(\frac {d^2 V}{d x^2}\) experimentalmente sus estados de menor energía. \(\ce{H2}\),\(\ce{Li2}\),\(\ce{O2}\),\(\ce{N2}\), y\(\ce{F2}\) han tenido términos hasta\(n < 10\) determinados de Ecuación\(\ref{taylor}\).

Connotaciones

La aproximación del Oscilador Armónico predice que sólo habrá una línea el espectro de una molécula diatómica, y mientras los datos experimentales muestran que de hecho hay una línea dominante, la fundamental, también hay otras líneas más débiles. ¿Cómo podemos dar cuenta de estas líneas extra?

Figura 13.5.3 : Diagrama para una molécula diatómica vibrante. Los niveles denotados por los números cuánticos vibracionales v representan la energía potencial para el oscilador armónico (cuadrático). La transición\( 0 \rightarrow 1 \) es la fundamental, las transiciones\( 0 \rightarrow n \) (n>1) se llaman armónicos, y las transiciones\( 1 \rightarrow n\) (n<1) se llaman transiciones calientes (bandas calientes).

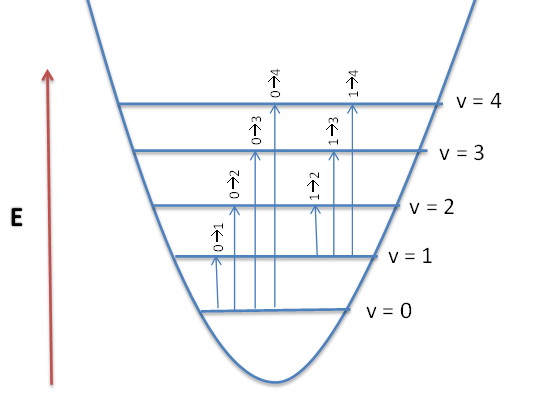
Cualquier frecuencia resonante por encima de la frecuencia fundamental se denomina sobretono. En el espectro IR, las bandas de sobretono son múltiplos de la frecuencia de absorción fundamental. Como puede recordar, los niveles de energía en la aproximación del Oscilador Armónico están espaciados uniformemente. La energía es proporcional a la frecuencia absorbida, que a su vez es proporcional al número de onda, el primer armónico que aparece en el espectro será el doble del número de onda del fundamental. Es decir, el primer armónico\(v = 1 \rightarrow 2\) es (aproximadamente) el doble de la energía de lo fundamental,\(v = 0 \rightarrow 1\).

Figura 13.5.4 : Una visión exagerada de los niveles de energía. (a) sería el oscilador armónico, con los niveles de energía uniformemente espaciados. (b) sería la anarmónica, con los niveles de energía comprimiendo hasta que converjan.

Los niveles no están igualmente espaciados, como en el oscilador armónico, sino que disminuyen a medida que\(v\) aumenta, hasta que finalmente converge, está implícito en la Figura 13.5.4 . También como consecuencia de la anarmonicidad, la regla de\(\Delta v= \pm 1\) selección ya no es válida y\(v\) puede ser cualquier número. Esto lleva a la observación de transiciones de orden superior, o armónicos, que resultan de la transición del estado fundamental a niveles de energía más altos.

Reglas de selección de osciladores anarmónicos

Para el oscilador anarmónico, la regla de selección es\(\Delta V= \text{any number}\). Es decir, no hay reglas de selección (para transiciones de estado a estado)

Los armónicos ocurren cuando un modo vibracional se excita de\(v=0\) a\(v=2\) (el primer armónico) o\(v=0\) a\(v=3\) (el segundo armónico). Las transiciones fundamentales,\(v=\pm 1\), son las que ocurren con mayor frecuencia, y la probabilidad de armónicos disminuye rápidamente a medida\( \Delta v > \pm 1\) que aumenta. Basado en la aproximación del oscilador armónico, la energía de la transición armónica será aproximadamente\(v\) veces la fundamental asociada con esa transición particular. Los cálculos del oscilador anarmónico muestran que los armónicos suelen ser menores que un múltiplo de la frecuencia fundamental. Los armónicos generalmente no se detectan en moléculas más grandes.

Esto se demuestra con las vibraciones de lo diatómico\(\ce{HCl}\) en la fase gaseosa:

Tabla 13.5.1 : Espectro vibracional de HCl.

Transición	obs [cm ^-1]	obs Armónico [cm ^-1]	obs Anarmónica [cm ^-1]
\( 0 \rightarrow 1 \)(fundamental)	2885.9	2885.9	2,885.3
\( 0 \rightarrow 2 \)(primer armónico)	5668.0	5771.8	5,665.0
\( 0 \rightarrow 3 \)(segundo armónico)	8347.0	8657.7	8,339.0
\( 0 \rightarrow 4\)(tercer armónico)	10 923.1	11 543.6	10,907.4
\( 0 \rightarrow 5\)(cuarto armónico)	13 396.5	14 429.5	13,370

Podemos ver en la Tabla 13.5.1 que las frecuencias anarmónicas corresponden mucho mejor con las frecuencias observadas, especialmente a medida que aumentan los niveles vibracionales. Debido a que los niveles de energía y armónicos están más cerca en el modelo anarmónico, también se alcanzan más fácilmente. Esto significa que existe una mayor probabilidad de que ese nivel posiblemente esté ocupado, lo que significa que puede aparecer como líneas de intensidad adicionales, aunque más débiles (la intensidad más débil indica una probabilidad menor de que ocurra la transición).

Ejercicio 13.5.1

\(\ce{HCl}\)tiene una banda fundamental a 2885.9 cm ⁻¹ y un armónico a 5668.1 cm ⁻¹ Calcular\(\tilde{\nu}\) y\( \tilde{\chi_e} \).

Ejercicio 13.5.2

Escribe la serie Taylor, y comenta la tendencia en los términos crecientes. Usando un número de prueba\(x\), agregue los términos 3, 4 y 5, luego compare esto con el término 2. ¿Cómo se comparan? Hemos visto que los términos anarmónicos aumentan la precisión de nuestra aproximación del oscilador. ¿Por qué no nos importan tanto los términos pasados del segundo?

Referencias

1. Espectros Infrarrojos y Raman de Compuestos Inorgánicos y de Coordinación. Parte A: Teoría y Aplicaciones en Química Inorgánica; Parte B: Aplicación en Química de Coordinación, Organometálica y Bioinorgánica, 5ª Edición (Nakamoto, Kazuo)
2. Lyle McAfee Revista de Educación Química 2000 77 (9), 1122
3. Stuart, Bárbara. Espectroscopia Infrarroja: Fundamentos y Aplicaciones. Wiley, 2004. Imprimir.