13.7: El principio Franck-Condon
- Page ID
- 79845
El Principio Franck-Condon describe las intensidades de las transiciones vibrónicas, o la absorción o emisión de un fotón. Afirma que cuando una molécula está experimentando una transición electrónica, como la ionización, la configuración nuclear de la molécula no experimenta ningún cambio significativo. Esto se debe de hecho a que los núcleos son mucho más masivos que los electrones y la transición electrónica tiene lugar más rápido de lo que los núcleos pueden responder. Cuando el núcleo se realinea con la nueva configuración electrónica, la teoría establece que debe sufrir una vibración.
Si imaginamos la transición vertical del estado terrestre al estado electrónico excitado como ocurriendo a partir de una función de onda vibracional que da una distribución de probabilidad de encontrar los núcleos en una región dada del espacio, podemos determinar la probabilidad de un nivel vibracional dado a partir de la integral de superposición\(S_{v’,v}\) que da la superposición de la función de onda vibracional en el suelo y estado excitado. Los números\(v’\) cuánticos se refieren al estado fundamental y los números\(v\) cuánticos se refieren al estado excitado. La probabilidad de transición se puede separar en partes electrónicas y nucleares usando la aproximación Condon.
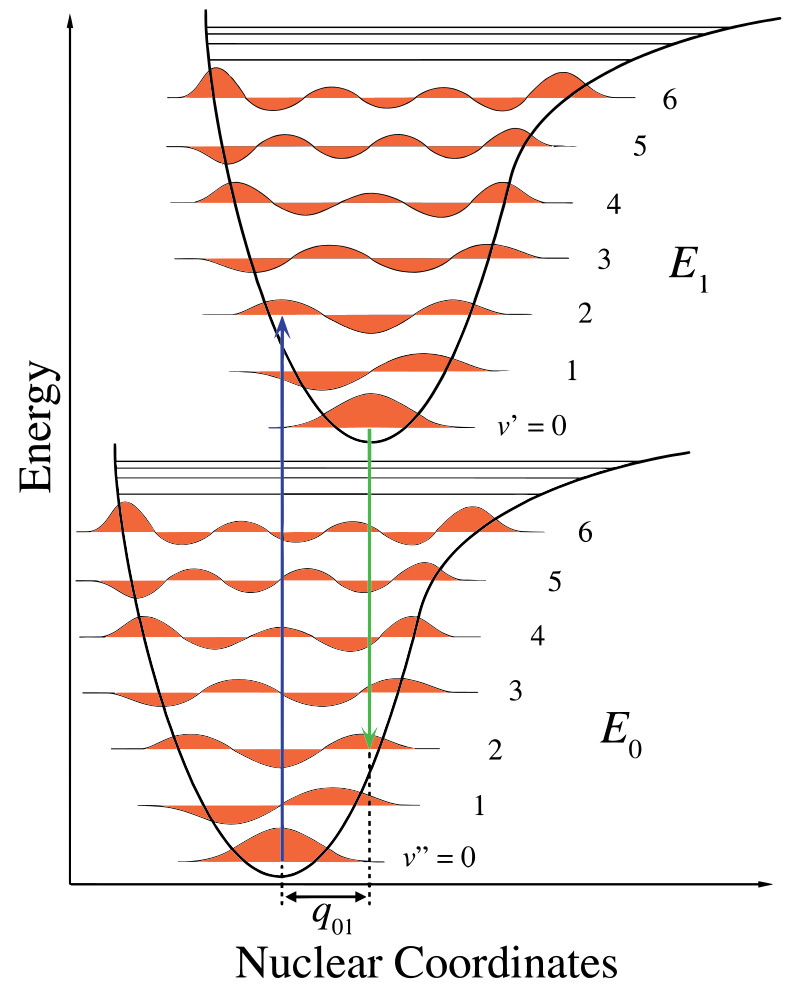
En la Figura 13.7.1 , el eje nuclear muestra una consecuencia de la separación internuclear y la transición vibrónica está indicada por las flechas verticales azul y verde. Esta cifra demuestra tres cosas:
- Una absorción conduce a un estado energético superior,
- la fluorescencia conduce a un estado de energía más bajo, y
- el cambio en las coordenadas nucleares entre el suelo y el estado excitado es indicativo de una nueva posición de equilibrio para el potencial de interacción nuclear. El hecho de que la flecha de fluorescencia sea más corta que la absorción indica que tiene menos energía, o que su longitud de onda es más larga.
La aproximación del condón es la suposición de que la transición electrónica se produce en una escala de tiempo corta en comparación con el movimiento nuclear, de manera que la probabilidad de transición se puede calcular en una posición nuclear fija.
Este cambio en la vibración se mantiene durante un estado denominado excitación electrónica rápida. Las fuerzas coulómbicas resultantes producen un equilibrio como se muestra en la figura para los núcleos denominados punto de inflexión. El punto de inflexión puede mapearse dibujando una línea vertical desde el mínimo de la curva inferior hasta la intersección del estado electrónico superior. Este procedimiento se denomina transición vertical y se discutió anteriormente en el contexto de la espectroscopía fotoelectrónica (otra espectroscopía electrónica).
El Principio Franck-Condon explica las intensidades relativas de las transiciones vibrónicas al relacionar la probabilidad de una transición vibracional con la superposición de las funciones de onda vibracionales. Afirma que la probabilidad de que ocurra una transición vibracional es ponderada por la integral de superposición Franck-Condon:
\[P_{i \rightarrow f} = | \langle \psi^*_{final} | \boldsymbol{\mu} | \psi_{initial} \rangle | ^2 = | \int \psi^*_{final} \boldsymbol{\mu} \psi_{initial} d\tau | ^2 \nonumber \]
Dentro de la aproximación Franck-Condon, los núcleos se consideran “fijos” durante las transiciones electrónicas. Así, las transiciones electrónicas pueden considerarse transiciones verticales en curvas electrónicas de energía potencial (transiciones vierical en la Figura 13.7.1 ).
El Principio Franck-Condon tiene una aplicación tanto Clásica como Cuántica. Clásicamente, el principio Franck—Condon es la aproximación de que es más probable que ocurra una transición electrónica sin cambios en las posiciones de los núcleos en la entidad molecular y su entorno. El estado resultante se llama estado Franck—Condon, y la transición involucrada, una transición vertical. La formulación mecánica cuántica de este principio es que la intensidad de una transición vibrónica es proporcional al cuadrado de la integral de superposición entre las funciones de onda vibracional de los dos estados que están involucrados en la transición.
El principio Franck-Condon se basa en la aproximación Born-Oppenheimer, que permite la separación de las funciones de\(Q\) onda electrónica\(q\) y nuclear dada la función de onda total.
\[ | \psi_{total}(Q,q) = | \psi_{nuc}(Q) \rangle \psi_{el} (Q;q) \rangle \nonumber \]
Dado que el operador de transición\(\hat{\mu}(q)\),, depende únicamente del componente electrónico, los componentes nucleares pueden separarse de la integral del momento de transición que dicta la probabilidad de que ocurra la transición:
\[ \begin{align} \langle \psi^{*}_{total, f} | \hat{\mu} | \psi_{total, i} \rangle &= \langle \psi^*_{nuc, f} | \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle | \psi_{nuc, i} \rangle \\[4pt] &= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{nuclear overlap}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle \end{align} \nonumber \]
Si la integral de superposición nuclear es cero para esta transición, entonces no se observará la transición, independientemente de la magnitud del factor electrónico.
\(S_{00}\)Transición evaluada dentro del modelo de oscilador armónico
El solapamiento nuclear para la transición cero-cero se\(S_{00}\) puede calcular simplemente usando la definición de la forma gaussiana de las funciones de onda del oscilador armónico.
La función de onda de punto cero en el estado electrónico de tierra es
\[ | \psi(R) \rangle = \big| \left(\dfrac{\alpha}{\pi} \right)^{1/4} e ^{-\alpha(R-R_e)^2/2} \big\rangle \nonumber \]
La función de onda de punto cero en el estado electrónico excitado es
\[ | \psi(R) \rangle = \big | \left(\dfrac{\alpha}{\pi} \right)^{1/4} e ^{-\alpha(R-Q_e)^2/2} \big\rangle \nonumber \]
donde
- \(\alpha = \dfrac{\sqrt{mk}}{\hbar}\)
- \(R_e\)es la longitud de enlace de equilibrio en el estado electrónico básico
- \(Q_e\)es la longitud del enlace de equilibrio en el estado electrónico excitado
La integral de superposición nuclear es
\[ S_{00}= \langle \psi^*_{nuc, f} | \psi_{nuc, i} \rangle = \sqrt{\dfrac{\alpha}{\pi}} \int_{\infty}^{\infty} e ^{-\alpha(R-R_e)^2/2} e ^{-\alpha(R-Q_e)^2/2} dR \label{FC1} \]
El exponente en la ecuación se\(\ref{FC1}\) puede expandir como
\[ S_{00}= \sqrt{\dfrac{\alpha}{\pi}} \int_{\infty}^{\infty} e ^{-\alpha(2R^2-RR_e - 2RQ_e+ R^2_e + Q_e^2)/2} dR \label{FC2} \]
y utilizamos
\[(R_e + Q_e)^2 = R_e^2 + Q_e^2 + 2R_eQ_e \nonumber \]
y
\[(R_e - Q_e)^2 = R_e^2 + Q_e^2 - 2R_eQ_e \nonumber \]
para sustituir y completar el cuadrado dentro de la integral. Podemos expresar
\[R_e^2 + Q_e^2 = \dfrac{1}{2}[(R_e + Q_e)^2 + (R_e - Q_e)^2]. \nonumber \]
Así, la integral en Ecuación\(\ref{FC2}\) es
\[S_{00}= \sqrt{\dfrac{\alpha}{\pi}} e^{-\alpha(R_e -Q_e)^2/4} \int_{-\infty}^{\infty} e ^{-\alpha\{R- 1/2(R_e+Q_e)\}^2} dR \nonumber \]
La integral es una integral gaussiana. Se puede demostrar que si dejamos\(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\) entonces\(dz = \sqrt{\alpha} dR\) y la integral se vuelve
\[S_{00}= \sqrt{\dfrac{\alpha}{\pi}} e^{-\alpha(R_e -Q_e)^2/4} \dfrac{1}{\sqrt{\alpha}} \int_{-\infty}^{\infty} e^{z^2} dz \label{FC3} \]
esta integral ya se ha resuelto, a partir de una tabla de integrales, la ecuación\(\ref{FC3}\) se vuelve
\[ S_{00} = e^{-\alpha(R_e-Q_e)^2/4} \nonumber \]
Seguiríamos el mismo procedimiento para calcular esa superposición de la vibración de nivel cero en el suelo al primer nivel vibracional excitado del estado excitado:\(S_{01}\).
\(S_{01}\)Transición evaluada dentro del modelo de oscilador armónico
Para calcular la superposición del nivel cero del estado fundamental (\(v=0\)) con el primer nivel de estado excitado (\(v'=1\)) utilizamos el polinomio Hermite\(H_1(x) =2x\) para describir la función de onda del estado excitado (ver aquí para una revisión sobre las funciones de onda del oscilador armónico). Aquí\(x = \sqrt{\alpha}(R - Q_e)\).
\[ S_{01}= \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle \label{FC01} \]
con la función de onda de punto cero en el estado electrónico de tierra es
\[ | \psi(R) \rangle = \big| \left(\dfrac{\alpha}{\pi} \right)^{1/4} e ^{-\alpha(R-R_e)^2/2} \big\rangle \nonumber \]
La primera función de onda de estado excitado en el estado electrónico excitado es
\[ | \psi(R) \rangle = \big | \left(\dfrac{\alpha}{\pi} \right)^{1/4} \sqrt{\alpha}2 (R-Q_e) e^{-\alpha(R-Q_e)^2/2} \big\rangle \nonumber \]
La superposición del nivel de estado fundamental cero con el primer nivel de estado excitado (Ecuación\(\ref{FC01}\)) es entonces
\[ S_{01} = \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{\alpha}{\pi}} \int_{-\infty}^{\infty} e^{-\alpha(R-R_e)^2/2} \sqrt{\alpha}2 (R-Q_e) e^{-\alpha(R-Q_e)^2/2} \nonumber \]
y
\[ S_{01} = \sqrt{\dfrac{2 \alpha^2}{\pi}} e^{-\alpha(R_e-Q_e)^2/4} \int_{-\infty}^{\infty} (R-Q_e) e^{-\alpha \{R- 1/2 (R_e+Q_e)^2\}} \nonumber \]
Se pueden hacer las mismas sustituciones que las anteriores para que la integral pueda escribirse como (no mostrada y para demostrarse en un ejercicio de tarea) y el resultado final es
\[S_{01} = \sqrt{\dfrac{\alpha^2}{2}} (R_e-Q_e) e^{-\alpha(R_e-Q_e)^2/4} \nonumber \]
Podríamos continuar y calcular ese solapamiento del nivel cero en el estado fundamental con todos los niveles vibracionales de luz superiores:\(S_{02}\),\(S_{03}\), etc. cada término corresponde a una transición con una energía diferente ya que los niveles vibracionales tienen diferentes energías. La banda de absorción tiene entonces la apariencia de una progresión (una progresión de Franck-Condon) de transiciones entre diferentes niveles cada uno con su propia probabilidad.
Progresiones Franck-Condon
Para comprender la significancia de la fórmula anterior para el factor FC, examinemos una superficie de energía potencial de tierra y estado excitado en\(T = 0\) Kelvin. A continuación se muestran dos estados separados por 8,000 cm -1 en energía. Esta es la separación de energía entre los fondos de sus pozos potenciales, pero también entre los respectivos niveles de energía de punto cero. Supongamos que el número de onda del modo vibratorio es de 1,000 cm -1 y que la longitud del enlace se incrementa debido a que un electrón se retira de un orbital de unión y se coloca en un orbital antienlace tras la excitación electrónica.
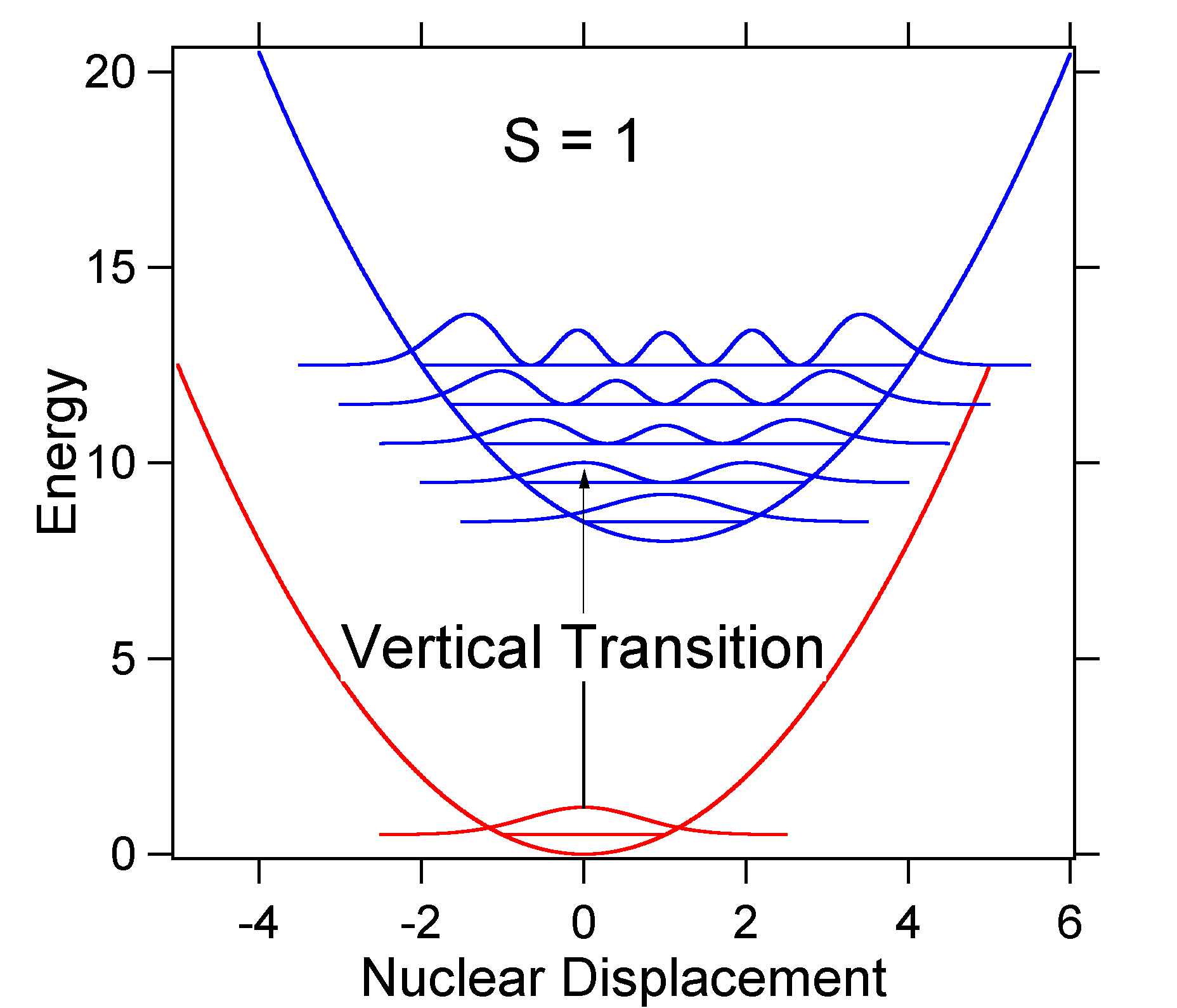
De acuerdo con el modelo anterior para el factor Franck-Condon generaríamos un espectro “stick” (Figura 13.7.3 ) donde cada transición vibracional es infinitamente estrecha y la transición sólo puede ocurrir cuando\(E = h\nu\) exactamente. Por ejemplo, las superficies de energía potencial se dieron para S = 1 y la probabilidad de transición en cada nivel viene dada por las barras (negras) en la siguiente figura.
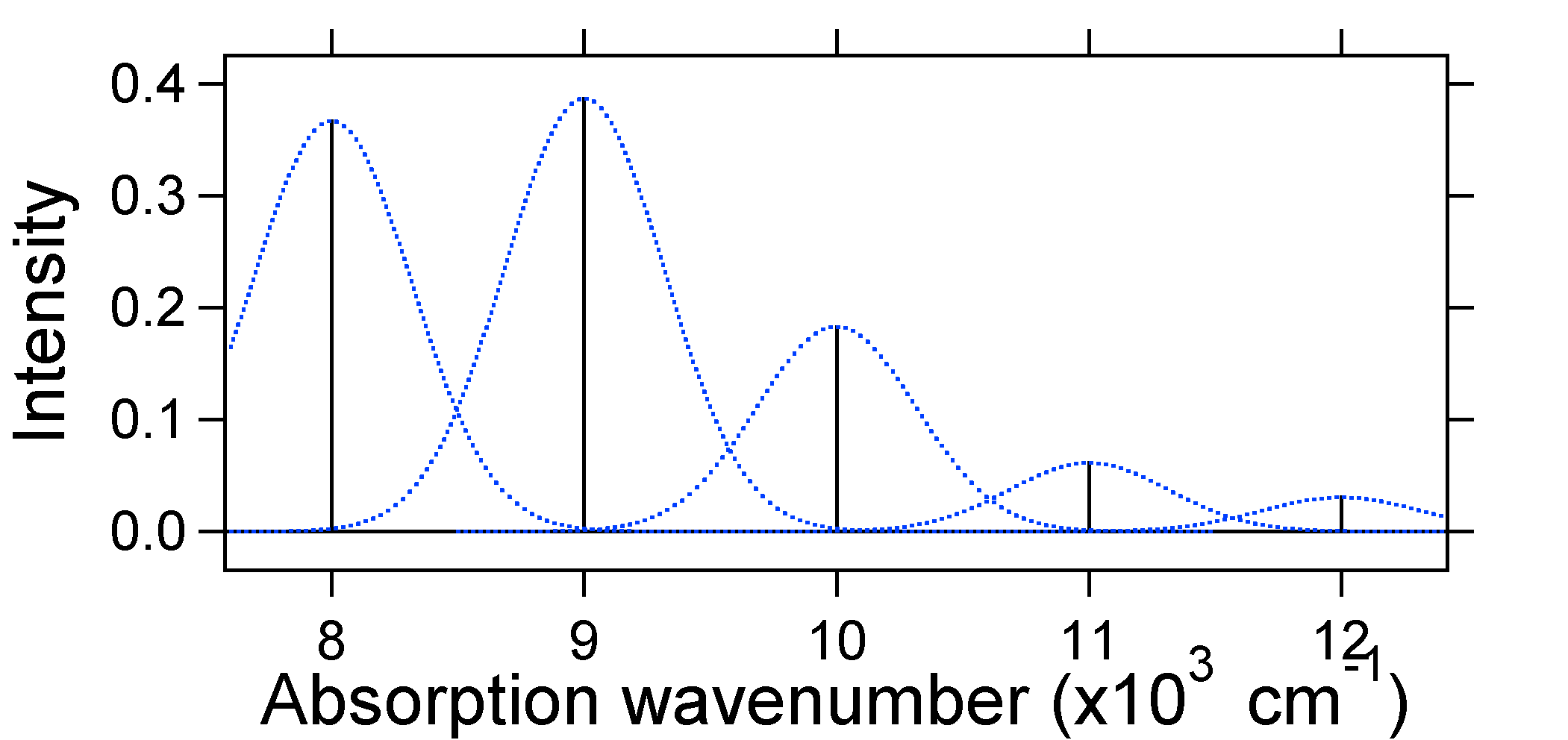
Los gaussianos punteados que rodean cada palo dan una imagen más realista de cómo debería ser el espectro de absorción. En este primer lugar a cada nivel de energía (stick) se le dará algún ancho por el hecho de que el estado tiene una vida útil finita. Dicho ensanchamiento se denomina ensanchamiento homogéneo ya que afecta a todas las moléculas del conjunto de manera similar. También hay ensanchamiento debido a pequeñas diferencias en el ambiente de cada molécula. Este tipo de ensanchamiento se denomina ensanchamiento no homogéneo. Independientemente del origen, el modelo anterior fue creado usando un ensanchamiento gaussiano
El desplazamiento nuclear entre el suelo y el estado excitado determina la forma del espectro de absorción. Examinemos tanto un desplazamiento de estado excitado más pequeño como uno grande. Si\(S = ½\) y las superficies de energía potencial en este caso son:
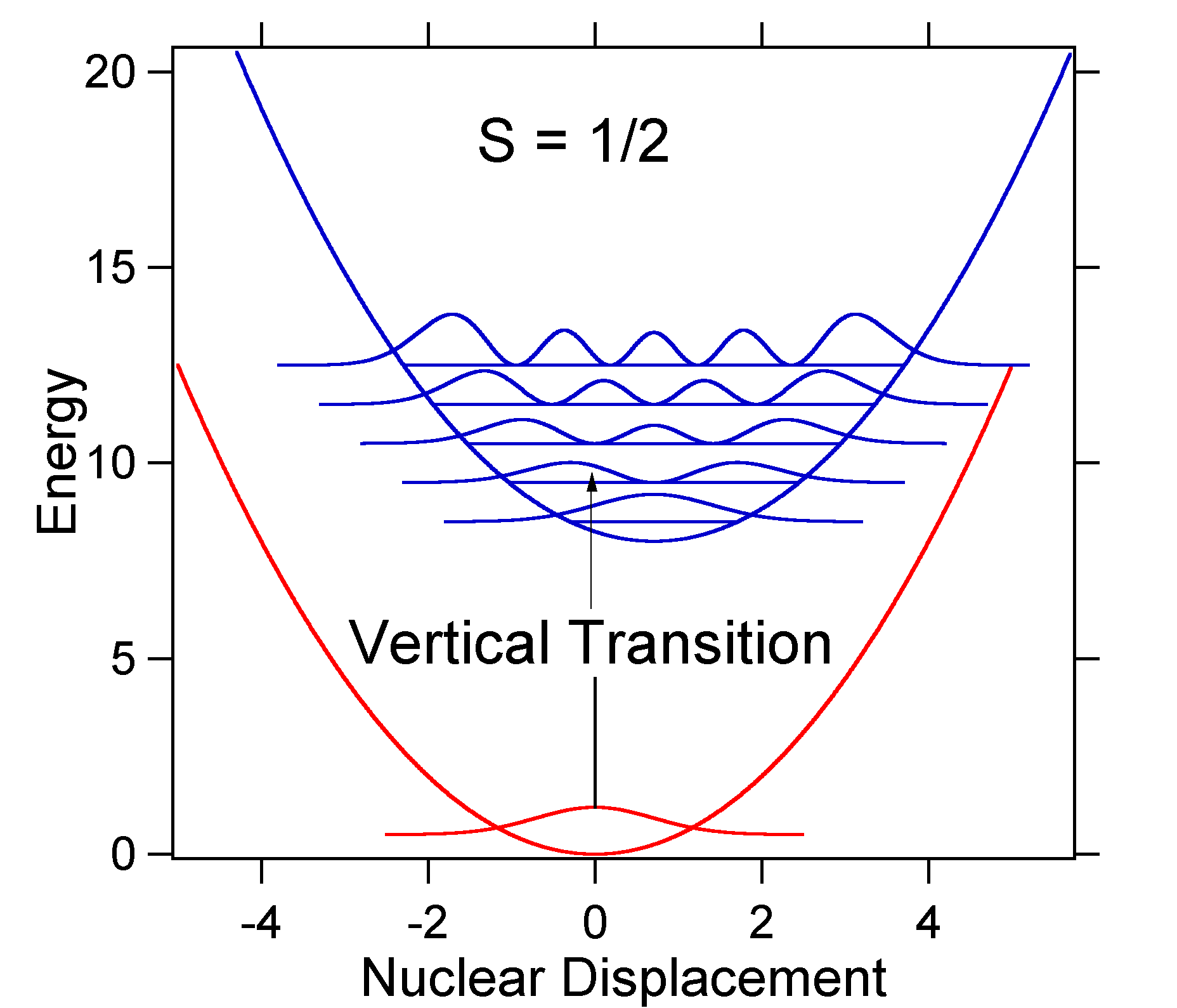
Para este caso el espectro “stick” tiene la apariencia en la Figura 13.7.5
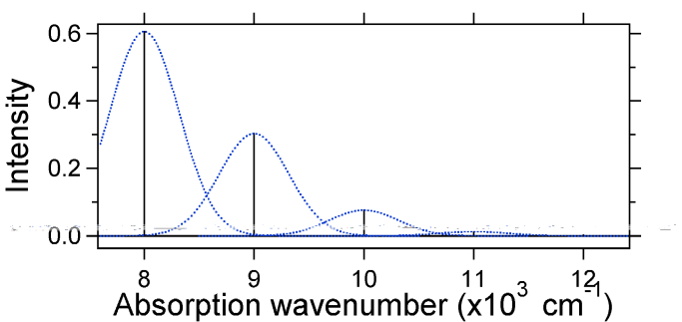
Tenga en cuenta que la transición de cero cero o\(S_{0,0}\) vibracional es mucho mayor en el caso de que el desplazamiento sea pequeño.
Como regla general, la\(S\) constante da la relación de la intensidad de la\(v = 2\) transición a la\(v = 1\) transición. En este caso ya que\(S = 0.5\), la\(v=2\) transición es 0.5 la intensidad de\(v=1\) transición.
Como ejemplo de un desplazamiento mayor se muestra a continuación la disposición de las superficies de energía potencial para S = 2.
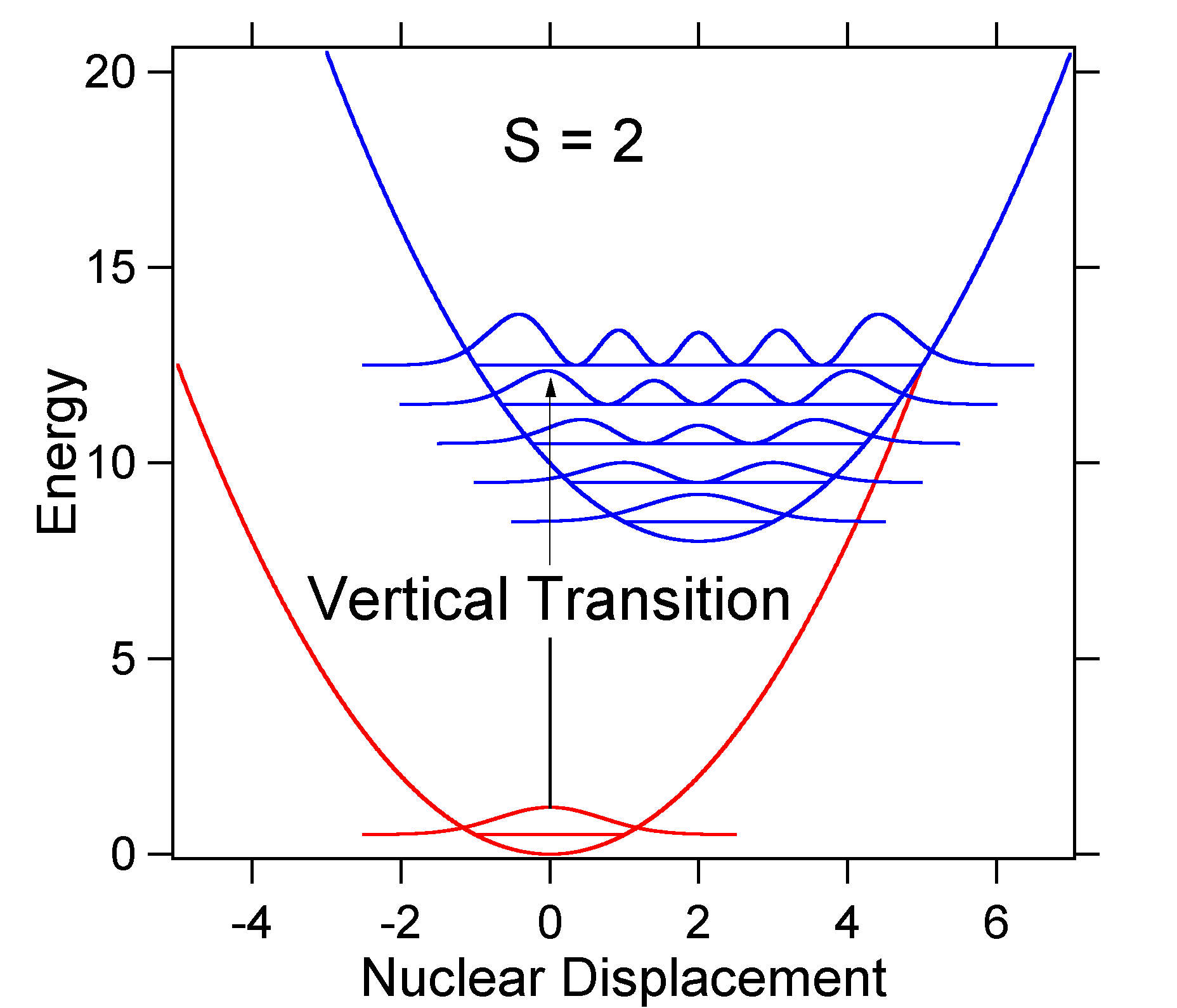
El mayor desplazamiento da como resultado una menor superposición del nivel de estado fundamental con el nivel v = 0 del estado excitado. La intensidad máxima se logrará en niveles vibracionales más altos como se muestra en el espectro del stick.
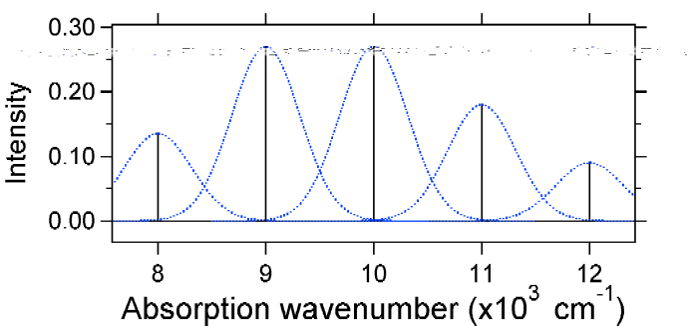
Los espectros de absorción trazados a continuación tienen la misma intensidad integrada, sin embargo sus formas se alteran debido a la diferente extensión de desplazamiento de la superficie de energía potencial del estado excitado.
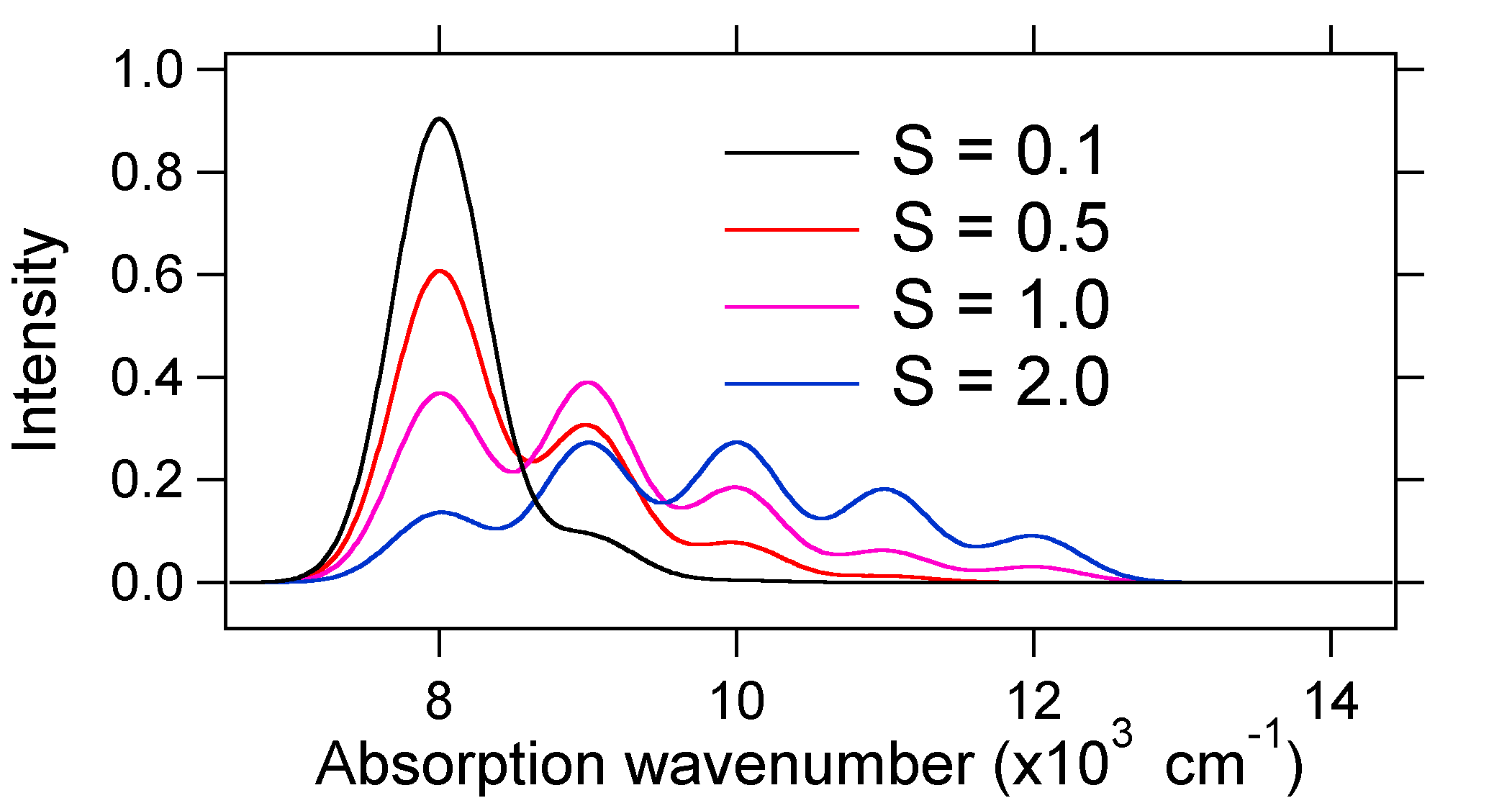
Entonces, la naturaleza de las intensidades relativas de la banda vibrónica puede decirnos si existe un desplazamiento de la coordenada nuclear de equilibrio que acompañó a una transición. ¿Cuándo habrá un aumento en la longitud del enlace (es decir,\(Q_e > R_e\))? Esto ocurre cuando un electrón es promovido desde un orbital molecular de enlace a un orbitales moleculares no enlazantes o antienlace (es decir, cuando el orden de enlace está menos en el estado excitado que en el estado fundamental).
- Orbital molecular sin\(\rightarrow\) unión de enlace orbital molecular
- Orbital molecular de\(\rightarrow\) unión orbital molecular antiunión
- Orbital molecular\(\rightarrow\) sin unión orbital molecular antiunión
En resumen, cuando el orden de enlace es menor en el estado excitado que en el estado base, entonces\(Q_e > R_e\); se producirá un aumento en la longitud del enlace cuando esto suceda.
Referencias
- Atkins, Peter y Julio de Paula. Química Física para las Ciencias de la Vida. 2006. Nueva York, NY: W.H. Freeman and Company. p. 563-564
- Principio Franck-Condon. 1996, 68, 2243. IUPAC Compendio de Terminología Química 2ª Edición (1997). www.iupac.org/goldbook/F02510.pdf
- E.Rabinowitch y Govindjee. Absorción de luz y destino de excitación de energía. 1969. Principio Franck-Condon. http://www.life.uiuc.edu/govindjee/b...em494/Abs.html

