13.8: Espectros rotacionales de Moléculas Poliatómicas
- Page ID
- 79818
Como se discutió anteriormente, la ecuación de Schrödinger para el movimiento angular de una molécula diatómica rígida (es decir, que tiene una longitud de enlace fija\(R\)) es
\[\dfrac{\hbar^2}{2 μ} \left[ \dfrac{1}{R^2 \sin θ} \dfrac{∂}{∂θ} \left(\sin θ \dfrac{∂}{∂θ} \right) + \dfrac{1}{R^2 \sin^2 θ} \dfrac{∂^2}{∂φ^2} \right] |ψ \rangle = E | ψ \rangle \nonumber \]
o
\[ \dfrac{L^2}{2 μ R^2 } | ψ \rangle = E | ψ\rangle \nonumber \]
El hamiltoniano en este problema contiene solo la energía cinética de rotación; no hay energía potencial presente porque la molécula está experimentando una “rotación libre” sin obstáculos. Los ángulos\(θ\) y\(φ\) describen la orientación del eje de la molécula diatómica en relación con un sistema de coordenadas fijado en laboratorio, y\(μ\) es la masa reducida de la molécula diatómica
\[ μ=\dfrac{m_1m_2}{m_1+m_2} \nonumber \]
Los valores propios correspondientes a cada función propia son sencillos de encontrar porque\(H_{rot}\) son proporcionales al\(L^2\) operador cuyos valores propios ya han sido determinados. Las energías rotacionales resultantes se dan como:
\[E_J= \dfrac{\hbar^2J(J+1)}{2μR^2} = B J(J+1) \label{Ediatomic} \]
y son independientes de\(M\). \(B\)es la constante de rotación. Por lo tanto, cada nivel de energía está etiquetado por\(J\) y es\(2J+1\) -fold degenerado (porque\(M\) varía de\(-J\) a\(J\)). La energía rotacional en la ecuación se\(\ref{Ediatomic}\) puede expresar en términos del momento de inercia\(I\)
\[I =\sum_i m_i R_i^2 \label{Idiatomic} \]
donde\(m_i\) está la masa del\(i^{th}\) átomo y\(R\) es su distancia del centro de masa de la molécula. Este momento de inercia reemplaza\(μR^2\) en el denominador de la Ecuación\(\ref{Ediatomic}\):
\[E_J= \dfrac{\hbar^2J(J+1)}{2I} = B J(J+1) \label{Ediatomic2} \]
Rotación de Moléculas Poliatómicas
A diferencia de las moléculas diatómicas (Ecuación\ ref {Idiatomic}), los movimientos rotacionales de las moléculas poliatómicas en tres dimensiones se caracterizan por múltiples momentos de inercia. típicamente reflejados en un tensor de\(3 \times 3\) inercia. Es común en la mecánica del cuerpo rígido expresar en estos momentos de inercia en coordenadas cartesianas basadas en laboratorio a través de una notación que identifica explícitamente los\(x\)\(y\),, y\(z\) ejes como\(I_{xx}\) y\(I_{xy}\), para los componentes del tensor de inercia.
\[I =\begin{bmatrix}I_{xx}&I_{xy}&I_{xz}\\I_{yx}&I_{yy}&I_{yz}\\I_{zx}&I_{zy}&I_{zz}\end{bmatrix} \label{inertiamatrix} \]
Los componentes de este tensor se pueden ensamblar en una matriz dada por
\[ I_{xx}=\sum _{k=1}^{N}m_{k}(y_{k}^{2}+z_{k}^{2}) \nonumber \]
\[ I_{yy}=\sum _{k=1}^{N}m_{k}(x_{k}^{2}+z_{k}^{2}) \nonumber \]
\[ I_{zz}=\sum _{k=1}^{N}m_{k}(x_{k}^{2}+y_{k}^{2}) \nonumber \]
\[ I_{yx}=I_{xy}=-\sum _{k=1}^{N}m_{k}x_{k}y_{k} \nonumber \]
\[ I_{zx}=I_{xz}=-\sum _{k=1}^{N}m_{k}x_{k}z_{k} \nonumber \]
\[ I_{zy}=I_{yz}=-\sum _{k=1}^{N}m_{k}y_{k}z_{k}. \nonumber \]
Los movimientos rotacionales de las moléculas poliatómicas se caracterizan por momentos de inercia que se definen en una molécula basada en coordenadas con ejes que están marcados\(a\),\(b\), y\(c\). Medida en el marco del cuerpo, la matriz de inercia (Ecuación\(\ref{inertiamatrix}\)) es una matriz simétrica real constante, que puede descomponerse en una matriz diagonal, dada por
\[ I =\left(\begin{array}{ccc}I_{a}&0&0\\0&I_{b}&0\\0&0&I_{c}\end{array}\right) \nonumber \]
Estas etiquetas se asignan de manera que\(I_c\) es el mayor momento principal de inercia con un orden de los tres momentos establecidos como
\[ I_a<I_b<I_c \nonumber \]
El operador de energía cinética rotacional para una molécula poliatómica rígida no lineal se expresa entonces como
\[H_{rot} = \dfrac{J_a^2}{2I_a} + \dfrac{J_b^2}{2I_b} + \dfrac{J_c^2}{2I_c} \label{genKE} \]
Los componentes de los operadores de momento angular mecánico cuántico a lo largo de los tres ejes principales son:
\[ \begin{align} J_a &= -i\hbar \cos χ \left[\cot θ \dfrac{∂}{∂χ} - (\sin θ )^{-1} \dfrac{∂}{∂φ} \right] - -i\hbar \sin χ \dfrac{∂}{∂θ} \\[4pt] J_b &= i\hbar \sin χ \left[\cot θ \dfrac{∂}{∂χ} - (\sin θ )^{-1} \dfrac{∂}{∂φ} \right] - -i\hbar \cos χ \dfrac{∂}{∂θ} \\[4pt] J_c &= - \dfrac{ih ∂}{∂χ} \end{align} \nonumber \]
Los ángulos\(θ\)\(φ\), y\(χ\) son los ángulos de Euler necesarios para especificar la orientación de la molécula rígida en relación con un sistema de coordenadas fijado en laboratorio. El cuadrado correspondiente del operador de momento angular total se\(J^2\) puede obtener como
\[ \begin{align} J^2 &= J_a^2 + J_b^ 2 + J_c^2 \\[4pt] & = - \dfrac{∂^2}{∂θ^2} - \cot θ \dfrac{∂}{∂θ} - \left(\dfrac{1}{\sin θ} \right) \left( \dfrac{∂^2}{∂φ^2} + \dfrac{∂^2}{∂χ^2} - 2 \cos θ \dfrac{∂^2}{∂φ∂χ} \right) \end{align} \nonumber \]
y el componente a lo largo del\(Z\) eje fijo en laboratorio es
\[J_Z = - ih \dfrac{∂}{∂φ}. \nonumber \]
Tops esféricos
Cuando los tres valores principales del momento de inercia son idénticos, la molécula se denomina una parte superior esférica. En este caso, la ecuación de energía rotacional total se\(\ref{genKE}\) puede expresar en términos del operador de momento angular total\(J^2\)
\[H_{rot} = \dfrac{J^2}{2I} \nonumber \]
Como resultado, las funciones propias de\(H_{rot}\) son las de\(J^2\) (y así\(J_a\) como\(J_Z\) ambas de las cuales conmutan con\(J_2\) y entre sí;\(J_Z\) es el componente de\(J\) a lo largo del eje Z fijo en laboratorio y conmuta con\(J_a\) porque
\[J_Z = - ih \dfrac{∂}{∂φ} \nonumber \]
y
\[J_a = - ih \dfrac{∂}{∂χ} \nonumber \]
actuar en diferentes ángulos. Las energías asociadas con tales funciones propias son
\[E(J,K,M) = \dfrac{\hbar^2 J(J+1)}{2I^2} \nonumber \]
para todos los K (es decir, J a números cuánticos) que van de -J a J en pasos unitarios y para todos los M (es decir, J Z números cuánticos) que van de -J a J. Cada nivel de energía es por lo tanto\((2J + 1)^2\) degenarado porque hay\(2J + 1\)\(2J + 1\) posibles valores K y posibles M valores para cada J. Las funciones propias de \(J^2\),\(J_Z\) y\(J_a\),\(|J,M,K>\) se dan en términos del conjunto de matrices de rotación\(D_{J,M,K}\):
\[|J,M,K \rangle = \sqrt{ \dfrac{2J + 1}{8 π^2}} D^* _{J,M,K} ( θ , φ , χ ) \nonumber \]
que obedecen
\[J^2 |J,M,K \rangle = \hbar^2 J(J+1) | J,M,K \rangle \nonumber \]
\[J_a |J,M,K \rangle = \hbar K | J,M,K \rangle \nonumber \]
\[J_Z |J,M,K \rangle = \hbar M | J,M,K \rangle \nonumber \]
Tops simétricos
Las partes superiores simétricas son moléculas con dos ejes rotacionales que tienen la misma inercia y un eje rotacional único con una inercia diferente. Las partes superiores simétricas se pueden dividir en dos categorías en función de la relación entre la inercia del eje único y la inercia de los dos ejes con inercia equivalente. Si el eje rotacional único tiene una inercia mayor que los ejes degenerados, la molécula se denomina una parte superior simétrica oblata (Figura 13.8.1 ). Si el eje rotacional único tiene una inercia menor que los ejes degenerados, la molécula se llama una parte superior simétrica prolada. Para la simplificación piense en estas dos categorías ya sea como frisbees para tops oblatos o balones de fútbol para copas proladas.
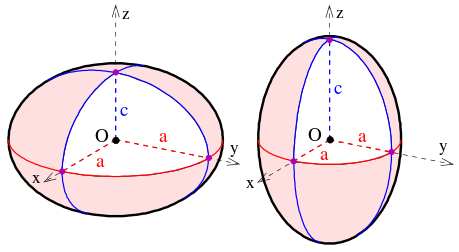
Nuevamente, la energía cinética rotacional, que es la hamiltoniana rotacional completa, se puede escribir en términos del operador de momento angular rotacional total\(J^2\) y la componente del momento angular a lo largo del eje con el único momento principal de inercia.
Para las puntas de prolado, la ecuación\(\ref{genKE}\) se convierte
\[H_{rot} = \dfrac{J^2}{2I} + J_a^2 \left( \dfrac{1}{2I_a} - \dfrac{1}{2I} \right) \nonumber \]
Para los tops oblatos, la ecuación\(\ref{genKE}\) se convierte en
\[H_{rot} = \dfrac{J^2}{2I} + J_c^2 \left( \dfrac{1}{2I_c} - \dfrac{1}{2I} \right) \nonumber \]
Como resultado, las funciones propias de\(H_{rot}\) son las de\(J^2\) y\(J_a\) o\(J_c\) (y de\(J_Z\)), y los niveles de energía correspondientes.
Las energías para las cimas proladas son
\[E(J,K,M) = \dfrac{h^2 J(J+1)}{2I^2} + h^2 K^2 \left( \dfrac{1}{2I_a} - \dfrac{1}{2I} \right) \nonumber \]
y las energías para las cimas oblatas son
\[E(J,K,M) = \dfrac{h^2 J(J+1)}{2I 2} + h^2 K^2 \left( \dfrac{1}{2I_c} - \dfrac{1}{2I} \right) \nonumber \]
nuevamente para K y M (es decir,\(J_a\) o\(J_c\) y números\(J_Z\) cuánticos, respectivamente) que van desde\(-J\) hasta\(J\) en pasos unitarios. Dado que la energía ahora depende de K, estos niveles solo son\(2J + 1\) degenerados debido a los\(2J + 1\) diferentes\(M\) valores que surgen para cada\(J\) valor. \(|J, M,K>\)Las funciones propias son las mismas funciones de matriz de rotación que surgen para el caso esférico superior.
Tops Asimétricos
Las funciones propias rotacionales y los niveles de energía de una molécula para la que los tres momentos principales de inercia son distintos (una parte superior asimétrica) no se pueden expresar fácilmente en términos de los estados propios de momento angular y los\(J\) números\(K\) cuánticos y los números.\(M\) Sin embargo, dados los tres momentos principales de inercia\(I_a\), y\(I_b\)\(I_c\), una representación matricial de cada una de las tres contribuciones al hamiltoniano rotacional general en Ecuación se\(\ref{genKE}\) puede formar dentro de un conjunto base de las funciones de la matriz de\(\{|J, M, K \rangle\}\) rotación. Esta matriz no será diagonal porque las\(|J, M, K \rangle\) funciones no son funciones propias de la parte superior asimétrica\(H_{rot}\). Sin embargo, la matriz se puede formar en esta base y posteriormente llevarla a forma diagonal al encontrar sus vectores propios {C n, J, M, K} y sus autovalores\(\{E_n\}\). Los coeficientes vectoriales expresan los estados propios asimétricos superiores como
\[\psi_n ( θ , φ , χ ) = \sum_{J, M, K} C_{n, J,M,K} |J, M, K \rangle \nonumber \]
Debido a que el momento angular total\(J^2\) aún viaja con\(H_{rot}\), cada uno de esos autoestados contendrá solo un valor J y, por lo tanto, también se\(Ψ_n\) puede etiquetar con un número\(J\) cuántico:
\[\psi _{n,J} ( θ , φ , χ ) = \sum_{M, K} C_{n, J,M,K} |J, M, K \rangle \nonumber \]
Para formar los únicos elementos de matriz distintos de cero\(H_{rot}\) dentro de la\(|J, M, K\rangle\) base, se pueden usar las siguientes propiedades de las funciones rotación-matriz:
\[\langle j, \rangle = \langle j, \rangle = 1/2 <j, \rangle = h 2 [ J(J+1) - K 2 ], \nonumber \]
\[ \langle j, \rangle = h^2 K^2 \nonumber \]
\[ \langle j \rangle = - \langle j \rangle = h^2 [J(J+1) - K(K ± 1)] 1/2 [J(J+1) -(K ± 1)(K ± 2)] 1/2 \langle j \rangle = 0 \nonumber \]
Cada uno de los elementos de\(J_c^2\)\(J_a^2\),, y\(J_b^2\) debe, por supuesto, ser multiplicado, respectivamente\(1/2I_c\), por\(1/2I_a\),\(1/2I_b\) y sumado juntos para formar la representación matricial de\(H_{rot}\). La diagonalización de esta matriz proporciona entonces las energías superiores asimétricas y las funciones de onda.


