13.9: Modos normales en moléculas poliatómicas
- Page ID
- 79859
Los modos normales se utilizan para describir los diferentes movimientos vibracionales en las moléculas. Cada modo puede caracterizarse por un tipo diferente de movimiento y cada modo tiene una cierta simetría asociada a él. La teoría de grupos es una herramienta útil para determinar qué simetrías contienen los modos normales y predecir si estos modos son IR y/o Raman activos. En consecuencia, la espectroscopia IR y Raman se utiliza a menudo para los espectros vibracionales.
Grados de Libertad
En general, un modo normal es un movimiento independiente de átomos en una molécula que ocurre sin causar movimiento a ninguno de los otros modos. Los modos normales, como implica su nombre, son ortogonales entre sí. Para discutir las ecuaciones cuántico-mecánicas que gobiernan las vibraciones moleculares es conveniente convertir las coordenadas cartesianas en las llamadas coordenadas normales. Las vibraciones en las moléculas poliatómicas están representadas por estas coordenadas normales.
Una molécula puede tener tres tipos de grados de libertad y un total de 3N grados de libertad, donde N es igual al número de átomos en la molécula. Estos grados de libertad pueden dividirse en tres categorías.
- Traslacional: Estos son los más simples de los grados de libertad. Estos conllevan el movimiento del centro de masa de la molécula entera. Este movimiento puede ser completamente descrito por tres vectores ortogonales y por lo tanto contiene 3 grados de libertad.
- Rotacional: Se trata de rotaciones alrededor del centro de masa de la molécula y al igual que el movimiento de traslación pueden ser completamente descritas por tres vectores ortogonales. Esto nuevamente significa que esta categoría contiene sólo 3 grados de libertad. Sin embargo, en el caso de una molécula lineal solo están presentes dos grados de libertad debido a la rotación a lo largo de los enlaces en la molécula que tiene una inercia insignificante.
- Vibracional: Se trata de cualquier otro tipo de movimiento no asignado al movimiento rotacional o traslacional y así hay 3N — 6 grados de libertad vibratoria para una molécula no lineal y 3N — 5 para una molécula lineal. Estas vibraciones incluyen flexión, estiramiento, meneo y muchos otros movimientos internos acertadamente nombrados de una molécula. Estas diversas vibraciones surgen debido a las numerosas combinaciones de diferentes estiramientos, contracciones y curvas que pueden ocurrir entre los enlaces de los átomos en la molécula.
| Grados totales de libertad | Grados de libertad traslacionales | Grados de libertad rotacional | Grados vibracionales de libertad | |
|---|---|---|---|---|
| Moléculas no lineales | 3N | 3 | 3 | 3N - 6 |
| Moléculas Lineales | 3N | 3 | 2 | 3N - 5 |
Cada uno de estos grados de libertad es capaz de almacenar energía. Sin embargo, en el caso de los grados de libertad rotacional y vibracional, la energía solo se puede almacenar en cantidades discretas. Esto se debe a la descomposición cuantificada de los niveles de energía en una molécula descrita por la mecánica cuántica. En el caso de rotaciones la energía almacenada depende de la inercia rotacional del gas junto con el número cuántico correspondiente que describe el nivel de energía.
El etano,\(C_2H_6\) tiene ocho átomos (\(N=8\)) y es una molécula no lineal por lo que de los\(3N=24\) grados de libertad, tres son traslacionales y tres son rotacionales. Los 18 grados de libertad restantes son internos (vibracionales). Esto es consistente con:
\[3N -6 =3(8)-6=18 \nonumber \]
Dióxido de Carbono,\(CO_2\) tiene tres átomos (\(N=3\)y es una molécula lineal por lo que de los\(3N=9\) grados de libertad, tres son traslacionales y dos son rotacionales. Los 4 grados de libertad restantes son vibracionales. Esto es consistente con:
\[3N - 5 = 3(3)-5 = 4 \nonumber \]
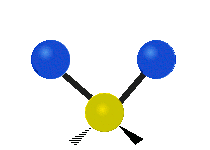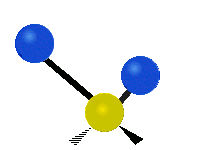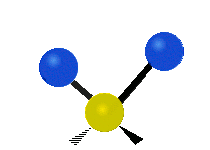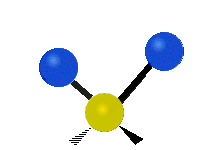
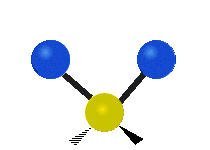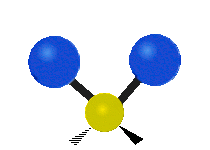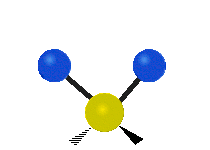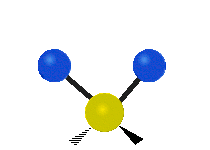
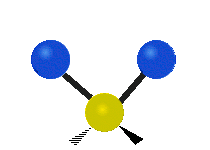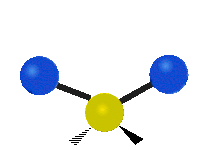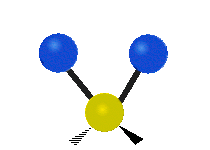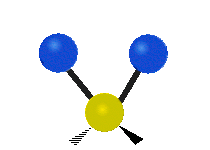
Los modos normales de vibración son: asimétrico, simétrico, meneo, torsión, tijera y balanceo para moléculas poliatómicas.
| Estiramiento simétrico | Estiramiento Asimétrico | meneando |
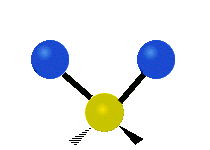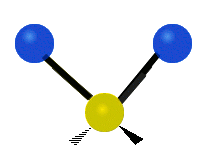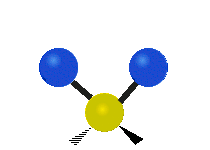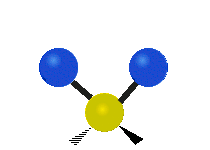 |
 |
 |
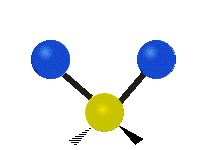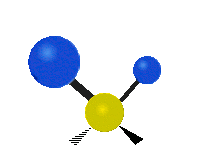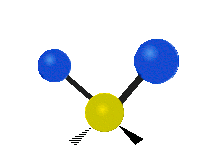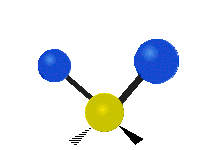
| Torcer | Tijera | R ocking |
 |
 |
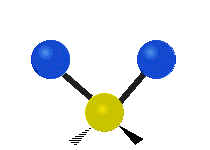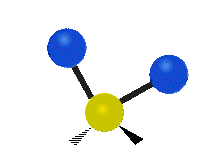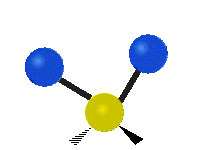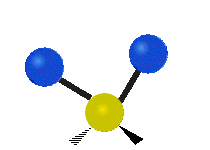 |
Figura 13.9.1 : Seis tipos de Modos Vibracionales. Tomado del editor en.wikipedia.org/wiki/Espectroscopía Infrared_con permiso del titular de los derechos de autor.
Modos normales
Si no hay campo externo presente, la energía de una molécula no depende de su orientación en el espacio (sus grados de libertad de traslación) ni de su centro de masa (sus grados de libertad rotacional). Por lo tanto, la energía potencial de la molécula se compone de sus grados vibracionales de libertad solo de\(3N-6\) (o\(3N-5\) para moléculas lineales). La diferencia en energía potencial viene dada por:
\[ \begin{align} \Delta V &= V(q_1,q_2,q_3,...,q_n) - V(0,0,0,...,0) \label{1} \\[4pt] &= \dfrac{1}{2} \sum_{i=1}^{N_{vib}} \sum_{j=1}^{N_{vib}} \left(\dfrac{\partial^2 V}{\partial q_i\partial q_j} \right) q_iq_j \label{2} \\[4pt] &= \dfrac{1}{2}\sum_{i=1}^{N_{vib}} \sum_{j=1}^{N_{vib}} f_{ij} q_iq_j \label{3} \end{align} \]
donde\(q\) representa el desplazamiento de equilibrio y\(N_{vib}\) el número de grados vibratorios de libertad.
Por simplicidad, los términos anarmónicos se descuidan en esta ecuación (es decir, se ignoran los términos de orden superior). Un teorema de la mecánica clásica afirma que los términos cruzados pueden eliminarse de la ecuación anterior (los detalles del teorema son muy complejos y no se discutirán en detalle). Mediante el uso de álgebra matricial se puede encontrar un nuevo conjunto de coordenadas {Q j} de tal manera que
\[\Delta{V} = \dfrac{1}{2} \sum_{j=1}^{N_{vib}}{F_jQ_j^2} \label{4} \]
Tenga en cuenta que no hay términos cruzados en esta nueva expresión. Estas nuevas coordenadas se denominan coordenadas normales o modos normales. Con estas nuevas coordenadas normales en la mano, el operador hamiltoniano para vibraciones se puede escribir de la siguiente manera:
\[\hat{H}_{vib} = -\sum_{j=1}^{N_{vib}} \dfrac{\hbar^2}{2\mu_i} \dfrac{d^2}{dQ_j^2} + \dfrac{1}{2} \sum_{j=1}^{N_{vib}}F_jQ_j^2 \label{5} \]
La función de onda total es un producto de las funciones de onda individuales y la energía es la suma de energías independientes. Esto lleva a:
\[ \hat{H}_{vib} = \sum_{j=1}^{N_{vib}} \hat{H}_{vib,j} = \sum_{j=1}^{N_{vib}} \left( \dfrac{-\hbar^2}{2 \mu_j}\dfrac{d^2}{dQ_i^2} + \dfrac{1}{2}\sum_{j=1}^{N_{vib}} F_jQ_j^2 \right) \label{6} \]
y la función de onda es entonces
\[\begin{align*} \psi_{vib} &= Q_1,Q_2, Q_3 ..., Q_{vib} \\[4pt] &= \psi_{vib,1}(Q_1) \psi_{vib,2}(Q_2) \psi_{vib,3}(Q_3) , ..., \psi_{vib,N_{vib}}(Q_{N_{vib}}) \end{align*} \nonumber \]
y la energía vibratoria total de la molécula es
\[E_{vib} = \sum_{j=1}^{N_{vin}} h\nu_j \left (v_j + \dfrac{1}{2}\right) \label{8} \]
donde\(v_j= 0,1,2,3...\).
La consecuencia del resultado expuesto en las ecuaciones anteriores es que cada modo vibracional puede ser tratado como una aproximación de oscilador armónico. Existen osciladores\(N_{vib}\) armónicos correspondientes al número total de modos vibracionales presentes en la molécula.
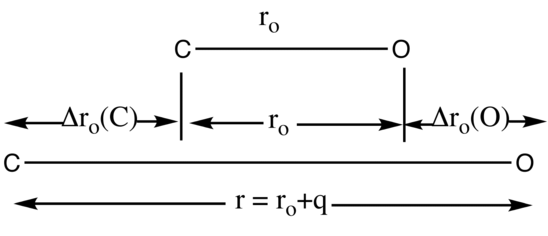
Descripción pictórica de coordenadas normales usando CO
La coordenada normal\(q\) se utiliza para seguir la trayectoria de un modo normal de vibración. Como se muestra en la Figura 13.9.2 el desplazamiento del\(\ce{C}\) átomo, denotado por\(Δr_o(\ce{C})\), y el desplazamiento del\(\ce{O}\) átomo, denotado por\(Δr_o(\ce{O})\), ocurren a la misma frecuencia. El desplazamiento de los átomos se mide a partir de la distancia de equilibrio en estado vibratorio terrestre,\(r_o\).