13.11: Teoría de la perturbación dependiente del tiempo

Última actualización
Guardar como PDF

Page ID: 79892

Wikipedia

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la teoría de la perturbación independiente del tiempo, la perturbación hamiltoniana es estática (es decir, no posee dependencia del tiempo). La teoría de la perturbación independiente del tiempo fue presentada por Erwin Schrödinger en un artículo de 1926, poco después de producir sus teorías en mecánica de olas. La teoría de perturbación dependiente del tiempo, desarrollada por Paul Dirac, estudia el efecto de una perturbación dependiente del tiempo $V (t)$ aplicada a un hamiltoniano independiente del tiempo$H_0$. Dado que el perturbado hamiltoniano depende del tiempo, también lo son sus niveles de energía y sus propios estados. Así, los objetivos de la teoría de perturbación dependiente del tiempo son ligeramente diferentes de la teoría de perturbación independiente del tiempo, donde uno puede estar interesado en las siguientes cantidades:

El valor de expectativa dependiente del tiempo de algunas $A$ observables, para un estado inicial dado.
Las amplitudes dependientes del tiempo de aquellos estados cuánticos que son bienes propios de energía (vectores propios) en el sistema imperturbado.

La primera cantidad es importante porque da lugar al resultado clásico de una medición realizada en un número macroscópico de copias del sistema perturbado. La segunda cantidad analiza la probabilidad de ocupación dependiente del tiempo para cada estado propio. Esto es particularmente útil en la física láser, donde uno está interesado en las poblaciones de diferentes estados atómicos en un gas cuando se aplica un campo eléctrico dependiente del tiempo. Examinaremos brevemente el método detrás de la formulación de Dirac de la teoría de perturbación dependiente del tiempo. Elija una base energética ${\ displaystyle {|n\ rangle}}$ $| n \rangle $para el sistema imperturbable. (Se caen los (0) superíndices para los autoestados, porque no es útil hablar de niveles de energía y autoestados para el sistema perturbado).

Si el sistema imperturbable está en estado propio a la vez$t = 0$, su estado$|j \rangle $ en momentos posteriores varía solo por una fase (esta es la imagen de Schrödinger, donde los vectores de estado evolucionan en el tiempo y los operadores son constantes)

\[|j(t)\rangle =e^{-iE_{j}t/\hbar }|j\rangle \nonumber \]

Ahora, introducir un hamiltoniano perturbador dependiente del tiempo$H_1(t)$. El hamiltoniano del sistema perturbado es

\[H=H_{0}+H_1(t) \nonumber \]

$|\psi (t)\rangle $Denote el estado cuántico del sistema perturbado en el momento$t$ y obedezca la ecuación de Schrödinger dependiente del tiempo,

\[H|\psi (t)\rangle =i\hbar {\dfrac {\partial }{\partial t}}|\psi (t)\rangle \nonumber \]

El estado cuántico en cada instante se puede expresar como una combinación lineal de la base propia completa de$ | n \rangle $:

\[|\psi (t)\rangle =\sum _{n}c_{n}(t)e^{-iE_{n}t/\hbar }|n\rangle \nonumber \]

donde se van a determinar las$c_n(t)$ coef $ficient$ s funciones complejas de $t$ a las que nos referiremos como amplitudes

Hemos extraído explícitamente los factores de fase exponenciales$\exp(-iE_{n}t/\hbar)$en el lado derecho. Esto es sólo una cuestión de convención, y puede hacerse sin pérdida de generalidad. La razón por la que nos vamos a este problema es que cuando el sistema arranca en el estado ${\ displaystyle |j\ rangle}$ $|j\rangle $y no hay perturbación presente, las amplitudes tienen la propiedad conveniente que, para todos t,$c_j(t) = 1$ y$c_n(t) = 0$ si$n \neq j$.

El cuadrado de la amplitud absoluta$c_n(t)$ es la probabilidad de que el sistema esté en estado en el$n$ momento$t$, ya que

\[|\psi (t)\rangle =\sum _{n}c_{n}(t)e^{-iE_{n}t/\hbar }|n\rangle \nonumber \]

Conectándose a la ecuación de Schrödinger y utilizando el hecho de que$\partial/ \partial t$ actúa por una regla en cadena, se obtiene

\[\sum _{n}\left(i\hbar {\dfrac {\partial c_{n}}{\partial t}}-c_{n}(t)V(t)\right)e^{-iE_{n}t/\hbar }|n\rangle =0~. \nonumber \]

Al resolver la identidad frente a $V$ , ésta puede reducirse a un conjunto de ecuaciones diferenciales parciales para las amplitudes,

\[{\dfrac {\partial c_{n}}{\partial t}}={\dfrac {-i}{\hbar }}\sum _{k}\langle n|H_1(t)|k\rangle \,c_{k}(t)\,e^{-i(E_{k}-E_{n})t/\hbar }~. \nonumber \]

Los elementos de la matriz$H_1$ juegan un papel similar al de la teoría de perturbación independiente del tiempo, siendo proporcionales a la velocidad a la que las amplitudes se desplazan entre estados. Obsérvese, sin embargo, que la dirección del desplazamiento es modificada por el factor de fase exponencial. A lo largo de tiempos mucho más largos que la diferencia de energía$E_k − E_n$, la fase serpentea alrededor de 0 varias veces. Si la dependencia del tiempo$H_1$ es suficientemente lenta, esto puede hacer que las amplitudes de estado oscilen (por ejemplo, tales oscilaciones son útiles para gestionar transiciones radiativas en un láser).

Sistema de dos niveles

Considere el sistema de dos niveles (i.e.$n=1,2$)

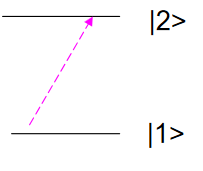
\[ | \psi \rangle = \sum_ {n=1,2} c_n(t) | n \rangle_o \nonumber \]

Solución de perturbación dependiente del tiempo para sistema de dos niveles:

\[ i \hbar \dfrac{\partial c_1(t)}{\partial t} = c_1(t) H_{11}(t) + c_2 e^{-i \omega_o t} H_{12} (t) \nonumber \]

\[ i \hbar \dfrac{\partial c_2(t)}{\partial t} = c_2(t) H_{22}(t) + c_1 e^{+i \omega_o t} H_{21} (t) \nonumber \]

donde los elementos de la matriz de la permutación (en términos de los autoestados de$H(0)$) son

\[ \langle m | H_1(t) | n \rangle = H_{mn}(t) \nonumber \]

Supongamos que el estado inicial es$n=1$, y$H_{11}=H_{22}=0$

\[ | \psi (t=0) \rangle = |1 \rangle \nonumber \]

Probabilidad de partícula en el$n=2$ momento$t$ posterior a la activación de la perturbación (es decir, luz incidente):

\[ c_2(t) = \dfrac{-i}{\hbar} \int_o^t e^{i \omega_o t} dt' H_{21}(t') \label{EQ1} \]

donde

\[H_1(t) = \cos (\omega t) V(r) \nonumber \]

$V(r)$es un vector de amplitud de polarización, que podemos ignorar por ahora.

Si asumimos que la frecuencia incidente de la luz incidente$\omega$ es comparable a la frecuencia natural de oscilación de$\omega _o$

\[\omega \approx \omega_o \nonumber \]

entonces la ecuación se$\ref{EQ1}$ puede simplificar a

\[c_2(t) = - \dfrac{2i}{\hbar} \dfrac{\sin (\omega-\omega_o)t /2}{ (\omega-\omega_o )t} e^{i (\omega_0-\omega)t/2} H_{21} \nonumber \]

Probabilidad de Transición

Supongamos que el estado inicial es$n=1$, y la probabilidad de transición de$n=1$ estado a$n=2$ estado es:

\[ P_{12}(t) = | c_2(t) |^2 =\dfrac{4}{\hbar^2} | \dfrac{\sin (\omega-\omega_o)t /2}{ (\omega-\omega_o )t} |^2 | H_{21} |^2 \nonumber \]

¿Qué significa esto? Extrañamente, significa que la probabilidad de hacer una transición en realidad está oscilando sinusoidalmente (¡al cuadrado)! Si quieres provocar una transición, debes desactivar la perturbación después del tiempo$\pi / |\omega- \omega_o| $ o algún múltiplo impar, cuando el sistema se encuentre en estado superior con máxima probabilidad.

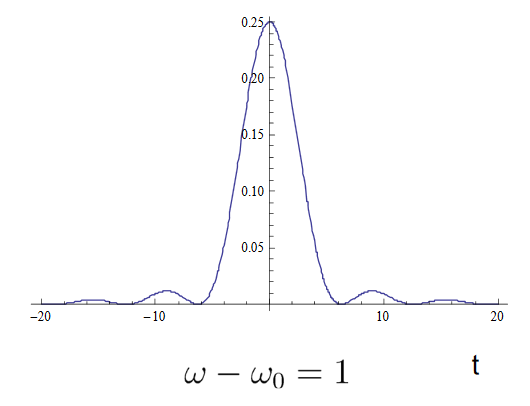
$P_{12}(t)$está alcanzado su punto máximo en$ \omega- \omega_o = 0$. La altura$ |H_{12}t/2 \hbar |^2$ y el ancho de$4\pi/t$ se hacen más altos y más estrechos a medida que pasa el tiempo. Recordemos que este es un tratamiento perturbador, sin embargo, y$P_{12}(t)$ no puede ser mayor que 1, por lo que la teoría de la perturbación se descompone eventualmente