17.2: La Distribución de Boltzmann representa una Distribución Termicamente Equilibrada
- Page ID
- 79572
Considera un conjunto de partículas N. Las partículas no son necesariamente indistinguibles y posiblemente tienen energía potencial mutua. Dado que este es un sistema grande, hay muchas formas diferentes de organizar sus partículas y, sin embargo, producir el mismo estado termodinámico. Solo puede ocurrir un arreglo a la vez. La suma de las probabilidades de cada arreglo separado equivale al número total de arreglos separados. Entonces la probabilidad de un sistema es:
\[p_N=W_N p_i \nonumber \]
donde\(p_N\) está la probabilidad del sistema,\(W_N\) es el número total de diferentes disposiciones posibles de las N partículas en el sistema, y\(p_i\) es la probabilidad de cada disposición separada. El principio de incertidumbre de Heisenberg establece que es imposible conocer simultáneamente el impulso y la posición de un objeto con total precisión. De acuerdo con el principio de incertidumbre, el número total posible de combinaciones puede definirse como el número total de reordenamientos distinguibles de las partículas de N.
El conjunto más práctico es el conjunto canónico con\(N\),\(V\), y\(T\) fijo. Podemos imaginar una colección de cajas con volúmenes iguales y número de partículas con toda la colección mantenida en equilibrio térmico. Con base en el factor Boltzmann, sabemos que para un sistema que tiene estados con energías\(e_1,e_2,e_3\)..., la probabilidad de\(p_j\) que el sistema esté en el estado\(j\) con energía\(E_j\) es exponencialmente proporcional a la energía del estado\(j\). Las funciones de partición del estado colocan un papel muy importante en el cálculo de las propiedades de un sistema, por ejemplo, se puede utilizar para calcular la probabilidad, así como la energía, la capacidad calorífica y la presión.
La distribución de Boltzmann
En última instancia, nos interesa la probabilidad de que ocurra una distribución determinada. La razón de esto es que debemos contar con esta información para obtener promedios termodinámicos útiles. Consideremos un conjunto de\(A\) sistemas. Definiremos\(a_j\) como el número de sistemas en el conjunto que se encuentran en el estado cuántico\(j\). Por ejemplo,\(a_1\) representa el número de sistemas en el estado cuántico 1. El número total de microestados posibles es:
\[W(a_1,a_2,...) = \frac{A!}{a_1!a_2!...} \nonumber \]
La probabilidad general de\(P_j\) que un sistema esté en el j ésimo estado cuántico se obtiene promediando\(a_j/A\) sobre todas las distribuciones permitidas. Así,\(P_j\) viene dado por:
\[ \begin{align*} P_j &= \dfrac{\langle a_j \rangle}{A} \\[4pt] &= \dfrac{1}{A} \dfrac{ \displaystyle \sum_a W(a) a_j(a)}{\displaystyle \sum_a W(a)} \end{align*} \]
donde los corchetes angulares indican un promedio de conjunto. Usando esta definición podemos calcular cualquier propiedad promedio (es decir, cualquier propiedad termodinámica):
\[ \langle M \rangle = \sum_j M_j P_j \label{avg} \]
El método de la distribución más probable se basa en la idea de que el promedio sobre\(P_j\) es idéntico a la distribución más probable. Físicamente, esto resulta del hecho de que tenemos tantas partículas en un sistema típico que las fluctuaciones de la media son extremadamente (inconmensurablemente) pequeñas. La equivalencia de la probabilidad promedio de un número de ocupación y la distribución más probable se expresa de la siguiente manera:
\[ P_j = \dfrac{\langle a_j \rangle}{A} = \dfrac{a_j}{A} \nonumber \]
La función de probabilidad está sujeta a las siguientes restricciones:
- Restricción 1: La conservación de la energía requiere:\[ E_{total} = \sum_j a_j e_j \label{con1} \] dónde\(e_j\) está la energía del jésimo estado cuántico.
- Restricción 2: La conservación de la masa requiere:\[ A = \sum_j a_j \label{con2} \] que dice solo que el número total de todos los sistemas en el conjunto es\(A\).
Como aprenderemos en capítulos posteriores, el sistema tenderá hacia la distribución de\(a_j\) que maximice el número total de microestados. Esto se puede expresar como:
\[\sum_j \left(\dfrac{\partial \ln W }{\partial a_j}\right) = 0 \nonumber \]
Nuestras limitaciones se convierten en:
\[ \sum_j e_j da_j =0 \nonumber \]
\[ \sum_j da_j =0 \nonumber \]
El método de multiplicadores Lagrange (llamado así por Joseph Louis Lagrange es una estrategia para encontrar los máximos y mínimos locales de una función sujeta a restricciones de igualdad. Usando el método de multiplicadores indeterminados LaGrange tenemos:
\[ \sum_j \left[ \left(\dfrac{\partial \ln W }{\partial a_j}\right)da_j + \alpha da_j - \beta e_j da_j \right] = 0 \nonumber \]
Podemos usar la aproximación de Stirling:
\[\ln x! \approx x\ln x – x \nonumber \]
evaluar:
\[ \left(\dfrac{\partial \ln W }{\partial a_j}\right) \nonumber \]
para obtener:
\[ \left(\dfrac{\partial A! }{\partial a_j}\right) - \sum_i \left(\dfrac{\partial \ln a_i }{\partial a_j}\right) = 0 \nonumber \]
como se indica a continuación.
Aplicación de la Aproximación de Stirling
El primer paso es señalar que:
\[\ln W = \ln A! - \sum_j \ln a_j! a \approx A \ln A – A - \sum_j a_j \ln a_j - \sum_j a_j \nonumber \]
Desde (de la ecuación\(\ref{con2}\)):
\[A = \sum_j a_j \nonumber \]
estos dos cancelan para dar:
\[\ln W = A \ln A - \sum_j a_j \ln a_j \nonumber \]
El derivado es:
\[ \left(\dfrac{\partial \ln W}{\partial a_j} \right) = \dfrac{\partial A \ln A}{\partial a_j} - \sum_i \dfrac{\partial a_i \ln a_i}{\partial a_j} \nonumber \]
Por lo tanto tenemos:
\[\left(\dfrac{\partial A \ln A}{\partial a_j} \right) = \dfrac{\partial A }{\partial a_j} \ln A - \dfrac{\partial A }{\partial a_j} = \ln A -1 \nonumber \]
\[\left(\dfrac{\partial a_i \ln a_i}{\partial a_j} \right) = \dfrac{\partial a_i }{\partial a_j} \ln a_i - \dfrac{\partial a_i }{\partial a_j} = \ln a_j +1 \nonumber \]
Estos últimos derivados resultan del hecho de que:
\[\left( \dfrac{\partial a_i}{\partial a_i} \right) = 1 \nonumber \]
\[\left( \dfrac{\partial a_j}{\partial a_i}\right)=0 \nonumber \]
La expresión simple que resulta de estas manipulaciones es:
\[ - \ln \left( \dfrac{a_j}{A} \right) + \alpha - \beta e_j =0 \nonumber \]
La distribución más probable es:
\[ \dfrac{a_j}{A} = e^a \sum_j e^{-\beta e_j} \label{Eq3} \]
Ahora necesitamos encontrar los multiplicadores indeterminados\(\alpha\) y\(\beta\).
El lado izquierdo de la Ecuación\(\ref{Eq3}\) es 1. Así, tenemos:
\[ P_j= \dfrac{a_j}{A} = \dfrac{ e^{-\beta e_j}} {\sum_j e^{-\beta e_j}} \nonumber \]
Esto determina\(a\) y define la distribución de Boltzmann. Mostraremos que\(\beta\) a partir del procedimiento de optimización del método de multiplicadores Lagrange se encuentra:
\[\beta=\dfrac{1}{kT} \nonumber \]
Esta identificación mostrará la importancia de la temperatura en la distribución de Boltzmann. La distribución representa una distribución más probable térmicamente equilibrada sobre todos los niveles de energía (Figura 17.2.1 ).
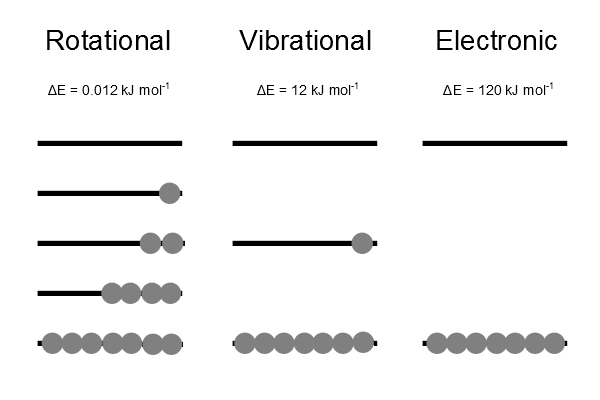
La distribución de Boltzmann representa una distribución más probable térmicamente equilibrada sobre todos los niveles de energía. Siempre hay una población mayor en un estado de menor energía que en uno de mayor energía.
Una vez que conocemos la distribución de probabilidad para la energía, podemos calcular propiedades termodinámicas como la energía, la entropía, las energías libres y las capacidades térmicas, que son todas cantidades promedio (Ecuación\(\ref{avg}\)). Para calcular\(P_j\), necesitamos los niveles de energía de un sistema (i.e.,\(\{e_i\}\)). La energía (“niveles”) de un sistema se puede construir a partir de los niveles de energía cuántica
Siempre hay que recordar que no importa cuán grande sea el espaciamiento de energía, siempre hay una probabilidad distinta de cero de que se poble el nivel superior. La única excepción es un sistema que está en cero absoluto. Sin embargo, esta situación es hipotética ya que el cero absoluto puede ser abordado pero no alcanzado.
Función de partición
A la suma sobre todos los factores\( e^{-\beta e_j} \) se le da nombre. Se llama la función de partición molecular,\(q\):
\[ q = \sum_j e^{-\beta e_j} \nonumber \]
La función de partición molecular\(q\) da una indicación del número promedio de estados que son térmicamente accesibles a una molécula a la temperatura del sistema. La función de partición es una suma sobre estados (por supuesto con el factor Boltzmann\(\beta\) multiplicando la energía en el exponente) y es un número. Más grande es el valor de\(q\), mayor es el número de estados que están disponibles para que el sistema molecular ocupe (Figura 17.2.2 ).
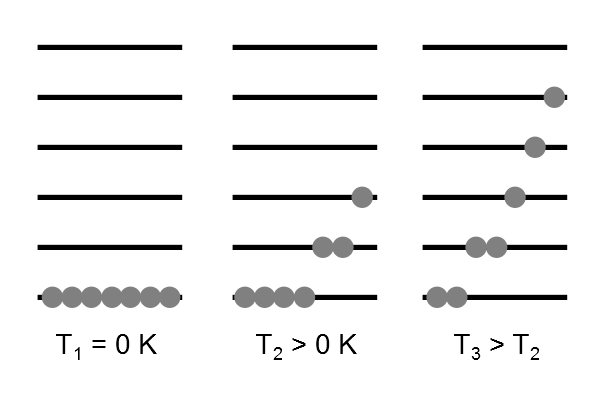
Aquí distinguimos entre la función de partición del conjunto,\(Q\) y la de una molécula individual,\(q\). Dado que\(Q\) representa una suma sobre todos los estados accesibles al sistema se puede escribir como:
\[ Q(N,V,T) = \sum_{i,j,k ...} e^{-\beta ( e_i + e_j +e_k ...)} \nonumber \]
donde los índices\(i,\,j,\,k\) representan los niveles de energía de diferentes partículas.
Independientemente del tipo de partícula la función de partición molecular,\(q\) representa los niveles de energía de una molécula individual. Podemos reescribir la suma anterior como:
\[Q = q_iq_jq_k… \nonumber \]
o:
\[Q = q^N \nonumber \]
para\(N\) partículas. Tenga en cuenta que\(q_i\) significa una suma sobre los estados o niveles de energía accesibles a la molécula\(i\) y\(q_j\) significa lo mismo para la molécula\(j\). La función de partición molecular,\(q\) cuenta los niveles de energía accesibles\(i\) solo a la molécula. \(Q\)cuenta no sólo los estados de todas las moléculas, sino todas las posibles combinaciones de ocupaciones de esos estados. No obstante, si las partículas no son distinguibles entonces habremos contabilizado\(N!\) estados demasiados. El factor de\(N!\) es exactamente cuántas veces podemos intercambiar los índices\(Q(N,V,T)\) y obtener el mismo valor (nuevamente siempre que las partículas no sean distinguibles). Vea este video para más información.
Referencias
- Hakala, R.W. (1967). Sencilla justificación de la forma de la ley de distribución de Boltzmann. Revista de Educación Química. 44 (11), 657. doi: 10.1021/ed044p657
- Grigorenko, I, García, M.E. (2002). Cálculo de la función de partición mediante algoritmos genéticos cuánticos. Physica A: Mecánica satística y sus aplicaciones. 313. 463-470. Recuperado a partir de http://www.sciencedirect.com/science...78437102009883
Problemas
- Completar la justificación de la ley de distribución de Boltzmann calculando la constante de proporcionalidad\(a\).
- Un sistema contiene dos niveles de energía\(E_1, E_2\). Utilizando las estadísticas de Boltzmann, expresar la energía promedio del sistema en términos de\(E_1, E_2\).
- Considera que un sistema contiene N niveles de energía. Rehacer problema #2.
- Utilice la propiedad de la función exponencial, derive ecuación (17.9).
- ¿Cuáles son los usos de las funciones de partición?

