18.4: La mayoría de las moléculas se encuentran en el estado vibratorio del suelo

Los niveles de energía vibratoria de un diatómico vienen dados por:

\[E_v = (v +1/2) h \nu \]

donde está\(\nu\) la frecuencia vibracional y\(v\) es el número cuántico vibracional. En este caso, es fácil sumar las series geométricas que se muestran a continuación:

\[\begin{align*} q_\text{vib} &= \sum_{v=0}^{\infty} e^{-( v + 1/2) h\nu / k T} \\[4pt] &= e^{-h \nu/ 2kT} \left( 1 + e^{-h \nu/ 2kT} + e^{-2 h \nu/ 2kT} + ... \right) \end{align*} \nonumber \]

o reescrito como:

\[ q_\text{vib} = e^{-h \nu / 2kT} \left( 1 +x + x^2 +x^3 + ... \right) \label{eq0} \]

donde\(x = e^{-h \nu/kT} \). Dada la siguiente expansión de la serie de potencia:

\[ \dfrac{1}{1 - x} = 1 + x + x^2 + x^3 + x^4 + .... \nonumber \]

La ecuación se\(\ref{eq0}\) puede reescribir como:

\[ q_\text{vib} = e^{-h \nu / 2kT} \left( \dfrac{1}{1-x} \right) \nonumber \]

o:

\[q_\text{vib} = \dfrac{e^{-h \nu / 2 k T}} {1 - e^{-h \nu/ k T}} \label{eq1} \]

Si el cero de la escala de energía está en\(h \nu /2kT\), entonces la ecuación se\(\ref{eq1}\) puede reescribir como:

\[q_\text{vib} \approx \dfrac{1} {1 - e^{-h \nu / kT}} \label{VIBQ} \]

Una temperatura vibratoria\(Θ_\text{vib}\) puede definirse como:

\[ Θ_\text{vib}= \dfrac{ hc \tilde{\nu}}{k} \nonumber \]

donde\(\tilde{\nu}\) es la frecuencia vibracional en cm ^-1. \(Θ_\text{vib}\)es una buena manera de expresar la rigidez de la unión vibratoria en unidades de la constante de Boltzmann. Debido a que la rigidez obviamente depende de qué enlace estés hablando, esta es una buena manera de hacer lo mismo que hicimos para la temperatura crítica de los gases no ideales.

Tabla 18.4.1 : Datos moleculares representativos para algunas diatómicas

Molécula	g	Longitud del enlace (pm)	\(ω\)(cm ^-1)	\(Θ_\text{vib}\)(K)	\(\tilde{B}\)(cm ^-1)	\(Θ_\text{rot}\)(K)	Constante de fuerza\(k\) (dinas/cm)	\(D_0\)(kcal/ mol)
\(H_2\)	1	0.7474	\ (ω\) (cm-1)” style="text-align:center; ">4400	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">6332	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">60.9	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">87.6	\ (k\) (dinas/cm)” style="text-align:center; ">5.749	\ (D_0\) (kcal/ mol) ">103.2
\(D_2\)	1	0.7415	\ (ω\) (cm-1)” style="text-align:center; ">3118	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">4487	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">30.45	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">43.8	\ (k\) (dinas/cm)” style="text-align:center; ">5.77	\ (D_0\) (kcal/ mol) ">104.6
\(N_2\)	1	1.097	\ (ω\) (cm-1)” style="text-align:center; ">2358	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">3393	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">2.001	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">2.99	\ (k\) (dinas/cm)” style="text-align:center; ">22.94	\ (D_0\) (kcal/ mol) ">225.1
\(O_2\)	3	1.207	\ (ω\) (cm-1)” style="text-align:center; ">1580	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">2274	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">1.446	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">2.08	\ (k\) (dinas/cm)” style="text-align:center; ">11.76	\ (D_0\) (kcal/ mol) ">118.0
\(Cl_2\)	1	1.987	\ (ω\) (cm-1)” style="text-align:center; ">560	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">805	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">0.244	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">0.351	\ (k\) (dinas/cm)” style="text-align:center; ">3.2	\ (D_0\) (kcal/ mol) ">57.0
\(CO\)	1	1.128	\ (ω\) (cm-1)” style="text-align:center; ">2170	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">3122	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">1.931	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">2.78	\ (k\) (dinas/cm)” style="text-align:center; ">19.03	\ (D_0\) (kcal/ mol) ">255.8
\(NO\)	2	1.15	\ (ω\) (cm-1)” style="text-align:center; ">190	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">2719	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">1.695	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">2.45	\ (k\) (dinas/cm)” style="text-align:center; ">15.7	\ (D_0\) (kcal/ mol) ">150.0
\(HCl\)	1	1.275	\ (ω\) (cm-1)” style="text-align:center; ">2938	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">4227	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">10.44	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">15.02	\ (k\) (dinas/cm)” style="text-align:center; ">4.9	\ (D_0\) (kcal/ mol) ">102.2
\(HI\)	1	1.609	\ (ω\) (cm-1)” style="text-align:center; ">2270	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">3266	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">6.46	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">9.06	\ (k\) (dinas/cm)” style="text-align:center; ">3.0	\ (D_0\) (kcal/ mol) ">70.5
\(Na_2\)	1	3.096	\ (ω\) (cm-1)” style="text-align:center; ">159	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">229	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">0.154	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">0.221	\ (k\) (dinas/cm)” style="text-align:center; ">0.17	\ (D_0\) (kcal/ mol) ">17.3
\(K_2\)	1	3.979	\ (ω\) (cm-1)” style="text-align:center; ">92.3	\ (θ_\ text {vib}\) (K)” style="text-align:center; ">133	\ (\ tilde {B}\) (cm-1)” style="text-align:center; ">0.0561	\ (θ_\ text {rot}\) (K)” style="text-align:center; ">0.081	\ (k\) (dinas/cm)” style="text-align:center; ">0.10	\ (D_0\) (kcal/ mol) ">11.8

Ejemplo 18.4.1

La frecuencia vibracional de de\(I_2\) es\(214.57\; cm^{-1}\). Calcular la función de partición vibracional de\(I_2\) a 300 K.

Solución:

\[\dfrac{h\nu}{kT} = \dfrac{ 214.57}{209.7} = 1.0232 \nonumber \]

por lo

\[e^{-h\nu/kT} = 0.3595 \nonumber \]

y

\[q_\text{vib} = \dfrac{1}{1-0.3595} = 1.561 \nonumber \nonumber \]

Esto implica, como antes, que muy pocos estados vibracionales son accesibles y mucho menos que los estados de rotación y muchos órdenes menos que los estados de traducción.

Capacidad de Calor Vibracional

La energía vibratoria viene dada por la expresión anterior y la capacidad calorífica molar a volumen constante,\(\bar{C}_V\) viene dada por:

\[ \bar{C}_V= \left(\dfrac{\partial E}{\partial T} \right)_V \nonumber \]

Contamos con:

\[ \begin{align} \dfrac{\partial }{\partial T} &= \dfrac{\partial \beta}{\partial T} \dfrac{∂}{\partial \beta} \\[4pt] &= \dfrac{-1}{kT^2} \dfrac{\partial }{\partial \beta} \\[4pt] &= \left(-k \beta^2 \right) \left(\dfrac{\partial }{\partial \beta}\right) \label{3.54} \end{align} \]

Por lo tanto:

\[\bar{C}_V = (-k \beta^2 ) \left(\dfrac{\partial ε_\text{vib}}{\partial \beta}\right) \nonumber \]

y cuando se introduce la función de partición vibracional (Ecuación\(\ref{VIBQ}\)):

\[\begin{align} q_\text{vib} &= -k \beta^2 \dfrac{ \left[ (1 - e^{-hc \nu / k T}) (-hc \tilde{\nu}) - e^{-hc \nu / k T} (+ hc\tilde{\nu}) \right] e^{-hc \nu / k T} }{ (1 - e^{-hc \nu / k T})^2 } hv \tilde{\nu} \\[4pt] &= k \left( \dfrac{ Θ_\text{vib} }{T} \right)^2 \dfrac{ e^{- Θ_\text{vib} /T} }{ \left( 1- e^{- Θ_\text{vib}/T} \right)^2 } \label{FinalQ} \end{align} \]

Para grandes\(T\), el\(\bar{C}_V\) se convierte en:

\[N_A k = R \nonumber \]

y para T pequeña,\(\bar{C}_V\) va a cero como se demuestra en la Figura 18.4.1 .

Figura 18.4.1 : Capacidad calorífica vibracional de un diatómico

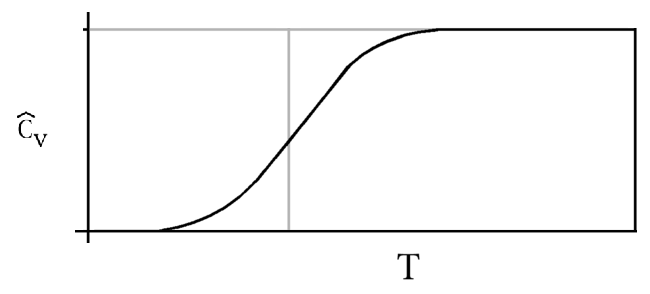
La capacidad calorífica vibracional se muestra como función de la temperatura reducida\(T/Θ\) para obtener una imagen general válida para todos los gases diatómicos. Compara los parámetros en la Tabla 18.4.1 para ver en qué diferentes escalas absolutas tenemos que pensar para diferentes gases. Claramente, la contribución vibratoria a la capacidad calorífica depende de la temperatura. Para muchas moléculas (especialmente las ligeras), la contribución vibratoria solo se activa a temperaturas bastante altas.

El valor de\(Θ_\text{vib}\) está determinado principalmente por

1. la fuerza de un vínculo (cuanto más fuerte es mayor\(Θ_\text{vib}\))
2. la masa (efectiva) de la molécula (cuanto más ligera, mayor\(Θ_\text{vib}\))

Las moléculas con baja\(Θ_\text{vib}\) frecuencia se disocian a temperaturas más bajas, aunque el modelo de oscilador armónico no es suficiente para describir ese fenómeno.

Poblaciones vibracionales

Podemos calcular la fracción de moléculas en cada estado vibratorio. La fracción de moléculas en\(v\) el estado vibracional viene dada por:

\[ f_v = \frac{e^{-h\nu(v+\frac{1}{2})/kT}}{q_\text{vib}} \]

Sustituyendo en Ecuación\(\ref{eq1}\), obtenemos:

\[\begin{split} f_v &= \left(1-e^{-h\nu/kT}\right)e^{-h\nu v/kT} \\ &=  \left(1-e^{-\Theta_\text{vib}/T}\right)e^{-\Theta_\text{vib} v/T} \end{split} \label{vib1} \]

Podemos trazar las moléculas de fracción en cada estado vibracional.

La población vibracional de Cl ₂ a 300 K. La mayoría de las moléculas se encuentran en el estado vibracional suelo,\(v=0\).

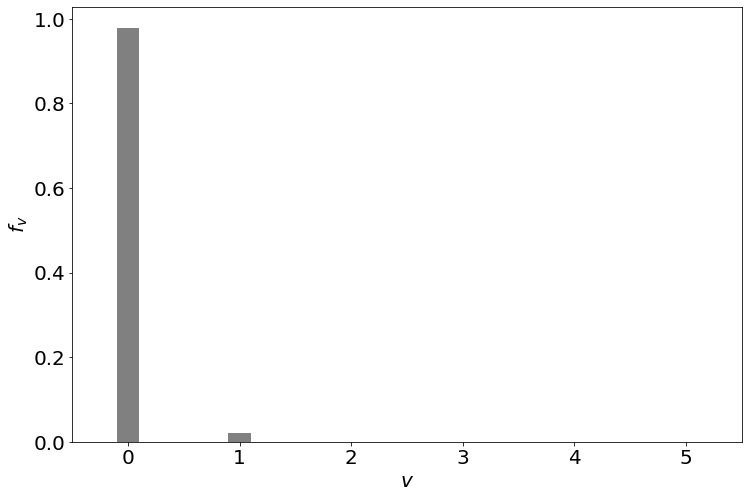
De la figura, podemos ver que la mayoría de las moléculas de Cl ₂ se encuentran en el estado vibratorio del suelo a temperatura ambiente (300 K). Esto es cierto para la mayoría de las moléculas. Solo las moléculas con enlaces muy débiles y bajas temperaturas vibracionales poblarán una fracción significativa de moléculas en estados vibracionales excitados.

Colaboradores y Atribuciones

• www.chem.iitb.ac.in/~bltembe/pdfs/ch_3.pdf