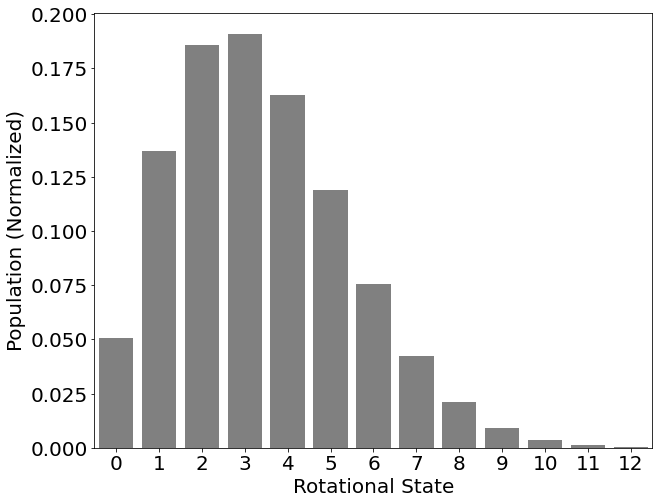
18.5: La mayoría de las moléculas se excitan rotacionalmente a temperaturas ordinarias
- Page ID
- 80095
El número cuántico rotacional es\(J\) y la energía de las rotaciones es:
\[E(J)= \tilde{B} J(J+1) \nonumber \]
Donde\(\tilde{B}\) está en unidades de cm -1 y es equivalente a:
\[\frac{h}{8\pi^2Ic} \nonumber \]
Dónde\(c\) está la velocidad de la luz en unidades de cm -1. Sin embargo, con la excepción del estado fundamental (es decir,\(J=0\)), existen múltiples autoestados para un valor dado de\(J\). Esta es una forma de degeneración, (\(g\)), y el número de niveles por energía va como 1, 3, 5, 7, 9 etc o:
\[g(J)=2J+1 \nonumber \]
Por lo tanto, la suma para encontrar la función de partición\(q_\text{rot}(T)\) contiene un factor extra\(g=2J+1\). Este factor es matemáticamente muy útil, porque es el derivado de:
\[g(J)=J(J+1) \nonumber \]
Esto permite cambiar variables a\(X=J(J+1)\) y la integración se vuelve muy fácil. Observe que al igual que en la función de partición de traducción, aproximamos la suma con una integral. No obstante, debido a que estamos lidiando con muchos menos niveles, esto está menos justificado en el caso rotacional. Lo justificado que esté depende del gas y de la temperatura que consideremos. En términos generales deberíamos estar a una temperatura\(T>> Θ_\text{rot}\).
Mira la tabla 18.2. ¿Cuándo necesitamos realmente elaborar la suma (discreta) en lugar de hacer una integración (continua) a partir de ella?
- Contestar
-
Solo para los gases más ligeros como\(\ce{He}\) y\(\ce{H2}\) tenemos que preocuparnos y luego solo en circunstancias criogénicas bastante bajas. A temperatura ambiente, podemos tomar los niveles rotacionales como un conjunto continuo y usar una integral. ¡Observe que los\(Θ\) valores vibracionales son mucho mayores! En\(T=300\,\text{K}\), por lo general sólo se ocupa un solo nivel y estamos en el límite discreto. En la superficie del sol eso sería una cuestión distinta por supuesto.
La constante rotacional\(B\) está directamente relacionada con el momento de inercia:
\[ I = μr^2\]
Dónde\(μ\) está la masa reducida de la molécula:
\[\dfrac{1}{μ} = \dfrac{1}{m_1} + \dfrac{1}{m_2} \nonumber \]
y\(r\) es la longitud del enlace. Nuevamente podemos escalar el comportamiento de diferentes sistemas a una misma imagen introduciendo una temperatura característica:
\[ \Theta_{rot} = \dfrac{hb}{k} = \dfrac{\hbar^2}{2Ik_b} \nonumber \]
Como hicimos para las traducciones, podemos calcular el momento\(\langle \epsilon \rangle\). Para las vibraciones obtenemos una función relativamente complicada de la temperatura. Sin embargo, para las rotaciones, el momento es simplemente igual a\(NkT\) y esto significa que la contribución rotacional al molar\(C_v\) de un diatómico es simplemente\(R\). Como las contribuciones vibracionales y electrónicas a la capacidad calorífica suelen ser insignificantes a temperatura ambiente, obtenemos:
- gas monatómico\[C_v= C_v^{trans} = \dfrac{3}{2} nR \nonumber \]
- diatómico\[\begin{align} C_v &= C_v^{trans}+C_v^{rot} \\[4pt] &= \dfrac{3}{2} nR + nR \\[4pt] &= \dfrac{5}{2}nR \end{align} \nonumber \]
Las energías rotacionales son menores que las energías vibracionales y electrónicas y, a temperatura ambiente, se poblarán muchos estados rotacionales.