18.7: Las funciones de partición vibracional de moléculas poliatómicas incluyen la función de partición para cada coordenada normal

Al igual que con las moléculas diatómicas, las energías de las moléculas poliatómicas pueden aproximarse por la suma de sus grados individuales de libertad. Por lo tanto, podemos escribir la función de partición como:

\[ Q(N,V,T) = \frac{[q(V,T)]^2}{N!} \]

Podemos escribir el análogo poliatómico a las moléculas diatómicas:

\[ Q(N,V,T) = \frac{(q_\text{trans}q_\text{rot}q_\text{vib}q_\text{elec})^N}{N!} \]

Cuando se derivó para moléculas diatómicas, asumimos el modelo de rotor rígido para rotaciones y el oscilador armónico para vibraciones. Esto nos permitió separar el movimiento rotacional del movimiento vibratorio de la molécula. Las moléculas poliatómicas son un poco más complicadas, pero todavía haremos uso de estas aproximaciones.

El número de estados traduccionales disponibles para cualquier molécula dada es mucho mayor que el número de moléculas en el sistema. \(q_\text{trans}\)viene dado por:

\[ q_\text{trans} = \left[\frac{2\pi MkT}{h^2}\right]^{3/2}V \]

donde\(M\) está la masa de la partícula. Pasando a la función de partición electrónica:

\[ q_\text{elec} = \sum_i{g_{i}e^{-E_i/kT}} \]

donde\(E_i\) está la energía del estado electrónico\(i\) y {g_i} es su degeneración. Los estados electrónicos suelen estar separados entre sí. La probabilidad de que el sistema esté en cualquier estado pero el estado base es extremadamente pequeña. Por lo tanto, podemos simplificar la función de partición electrónica para incluir solo el estado electrónico fundamental:

\[ q_\text{elec} = g_{e1}e^{D_e/kT} \]

donde\(-D_e\) está la energía del estado electrónico de tierra. Para completar la función de partición poliatómica, todavía necesitamos\(q_\text{vib}\) y\(q_\text{rot}\). Terminaremos esta sección con\(q_\text{vib}\) y hablaremos\(q_\text{rot}\) en la siguiente.

El movimiento vibracional de las moléculas diatómicas se puede expresar como un conjunto de osciladores armónicos independientes. Para las moléculas poliatómicas, los movimientos vibratorios independientes se denominan modos normales de vibración. La energía vibratoria es entonces la suma de las energías para cada modo normal:

\[ E_\text{vib} = \sum_i^\alpha{\left(v_i + \frac{1}{2}\right)h\nu} \]

donde\(\nu_i\) es la frecuencia vibracional para el modo normal\(i\) th y\(\alpha\) es el número de grados de vibración de libertad. Una molécula lineal tiene grados de libertad\(3n-5\) vibratoria y una molécula no lineal tiene grados de libertad\(3n-6\) vibracional. Debido a que los modos normales son independientes entre sí, podemos sacar resultados de secciones anteriores:

\[ q_\text{vib} = \prod_i^\alpha{\frac{e^{-\theta_{\text{vib},i}/2T}}{1-e^{-\theta_{\text{vib},i}/T}}} \]

\[ E_\text{vib} = Nk \sum_i^\alpha{\left( \frac{\theta_{\text{vib},i}}{2} + \theta_{\text{vib},i} \frac{e^{-\theta_{\text{vib},i}/T}}{1-e^{-\theta_{\text{vib},i}/T}} \right)}  \]

\[ C_{V,\text{vib}} = Nk \sum_i^\alpha{\left( \left(\frac{\theta_{\text{vib},i}}{2}\right)^2 + \frac{e^{-\theta_{\text{vib},i}/T}}{(1-e^{-\theta_{\text{vib},i}/T})^2} \right)}  \]

donde\(\theta_{\text{vib},i}\) es la temperatura vibracional característica definida por:

\[ \theta_{\text{vib},i} =\frac{h\nu_i}{k} \]

Entropía Vibracional

Existe una gran utilidad para las funciones termodinámicas calculadas a partir de los modos vibracionales normales de una molécula. La energía vibratoria y la entropía dependen de la forma de una superficie de energía potencial multidimensional. Si se realiza una búsqueda conformacional de macromoléculas se obtiene energías y estructuras pero poca información directa sobre la forma de la superficie de energía potencial para cada conformación. La entropía vibracional da una media que determina si existen diferencias entrópicas significativas en las estructuras y por lo tanto si se favorecerán ciertas conformaciones basadas en la entropía.

Sin embargo, es posible tomar combinaciones lineales apropiadas de las coordenadas para que se eliminen los términos cruzados y el hamiltoniano clásico así como el operador correspondiente no contenga términos cruzados y en términos de las nuevas coordenadas, el hamiltoniano puede escribirse como,

\[ H = \sum_{i=1}^{f} \dfrac{h^2}{2 \mu_i} \dfrac{\partial}{\partial q_i^2}+ \sum_{i=1}^{f} \dfrac{k_i}{2} q_i^2 \label{3.81} \]

Aquí, los grados de libertad\(f\) son\(3N - 5\) para una molécula lineal y\(3N - 6\) para una molécula no lineal. Aquí,\(k_i\) es la constante de fuerza y\(μ_i\) es la masa reducida para ese modo vibratorio particular que se conoce como un modo normal.

Figura 18.7.1 : Se muestran los tres modos vibracionales del agua, el estiramiento simétrico (3656.7 cm ^-1, 5160 K), el estiramiento asimétrico (3755.8 cm ^-1, 5360 K) y el modo de flexión (1594.8 cm ^-1 ,2290 K). Las frecuencias vibracionales y la temperatura característica para cada modo se muestran entre paréntesis. Aunque no se muestra en la animación, el átomo de oxígeno también se mueve con cada uno de estos modos normales.

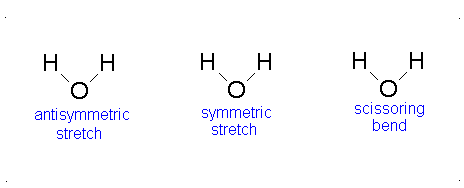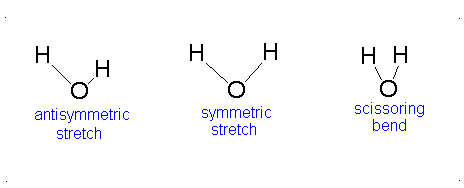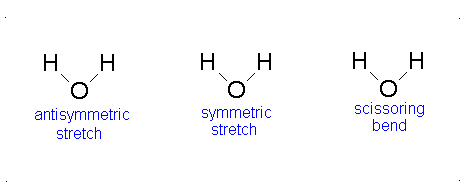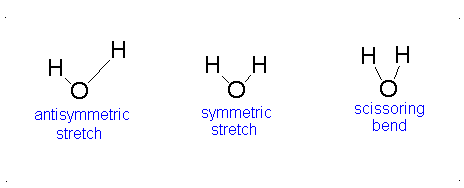
La Ecuación\(\ref{3.81}\) representa osciladores armónicos\(f\) linealmente independientes y la energía total para dicho sistema es

\[ \epsilon_{vib} = \sum_{i=1}^{f} \left( v_i + \dfrac{1}{2} \right) h \nu_i \nonumber \]

Las frecuencias vibracionales están dadas por

\[ \nu_i = \dfrac{1}{2 \pi} \sqrt{\dfrac{k_i}{\mu_i}} \nonumber \]

La función de partición vibracional viene dada por el producto de funciones\(f\) vibracionales para cada frecuencia.

\[ q_{vib} = \prod_{i=1}^f \dfrac{ e^{-\Theta_{vib,i}/2T} }{1- e^{-\Theta_{vib,i}/T}} \label{Qvib1} \]

con

\[ \Theta_{vib,i} = \dfrac{h\nu_i}{k_B} \nonumber \]

Al igual que con la discusión anterior respecto a la diatómica simple,\(\Theta_{vib,i}\) se llama la temperatura vibracional característica. Las energías molares y las capacidades térmicas vienen dadas por

\[ \langle E_{vib} \rangle = Nk \sum_{i=1}^f \left[ \dfrac{ \Theta_{vib,i} }{2} + \dfrac{ \Theta_{vib,i} e^{-\Theta_{vib,i}/T} }{1- e^{-\Theta_{vib,i}/T}} \right] \nonumber \]

y

\[ \bar{C}_V = Nk_B \sum_{i=1}^f \left( \dfrac{ \Theta_{vib,i} }{T} \right)^2 \dfrac{ e^{-\Theta_{vib,i}/T} }{\left(1- e^{-\Theta_{vib,i}/T}\right)^2} \nonumber \]

Ejemplo\(NO_2\)

Las tres temperaturas vibracionales características para\(\ce{NO2}\) son 1900 K, 1980 K y 2330 K. Calcular la función de partición vibratoria a 300 K.

Solución

La partición vibracional es (Ecuación\(\ref{Qvib1}\))

\[ q_{vib} = \prod_{i=1}^f \dfrac{ e^{-\Theta_{vib,i}/2T} }{1- e^{-\Theta_{vib,i}/T}} \nonumber \]

Si calculamos\(q_{vib}\) tomando las energías del punto cero como los puntos de referencia con respecto a los cuales se miden las otras energías

\[\begin{align*} q_{vib} &= \prod_{i=1}^f \dfrac{ 1 }{1- e^{-\Theta_{vib,i}/T}} = \left( \dfrac{ 1 }{1- e^{-1900/300}} \right) \left( \dfrac{ 1 }{1- e^{-1980/300}} \right) \left( \dfrac{ 1 }{1- e^{-2330/300}} \right) \\[4pt] & =(1.0018) ( 1.0014)(1.0004) = 1.0035 \end{align*} \nonumber \]

La implicación es que muy pocos estados vibracionales de\(\ce{NO2}\) (aparte del estado vibratorio del suelo) son accesibles a 300 K. Esto es estándar de las vibraciones de la mayoría de las moléculas.

Colaboradores y Atribuciones

• www.chem.iitb.ac.in/~bltembe/pdfs/ch_3.pdf