23.2: Energías Gibbs y Diagramas de Fase
- Page ID
- 79621
Transiciones de primer orden
La siguiente gráfica muestra la energía de Gibbs en función de la temperatura, incluyendo cambios de fase de sólido a líquido (fusión) y líquido a gas (ebullición).
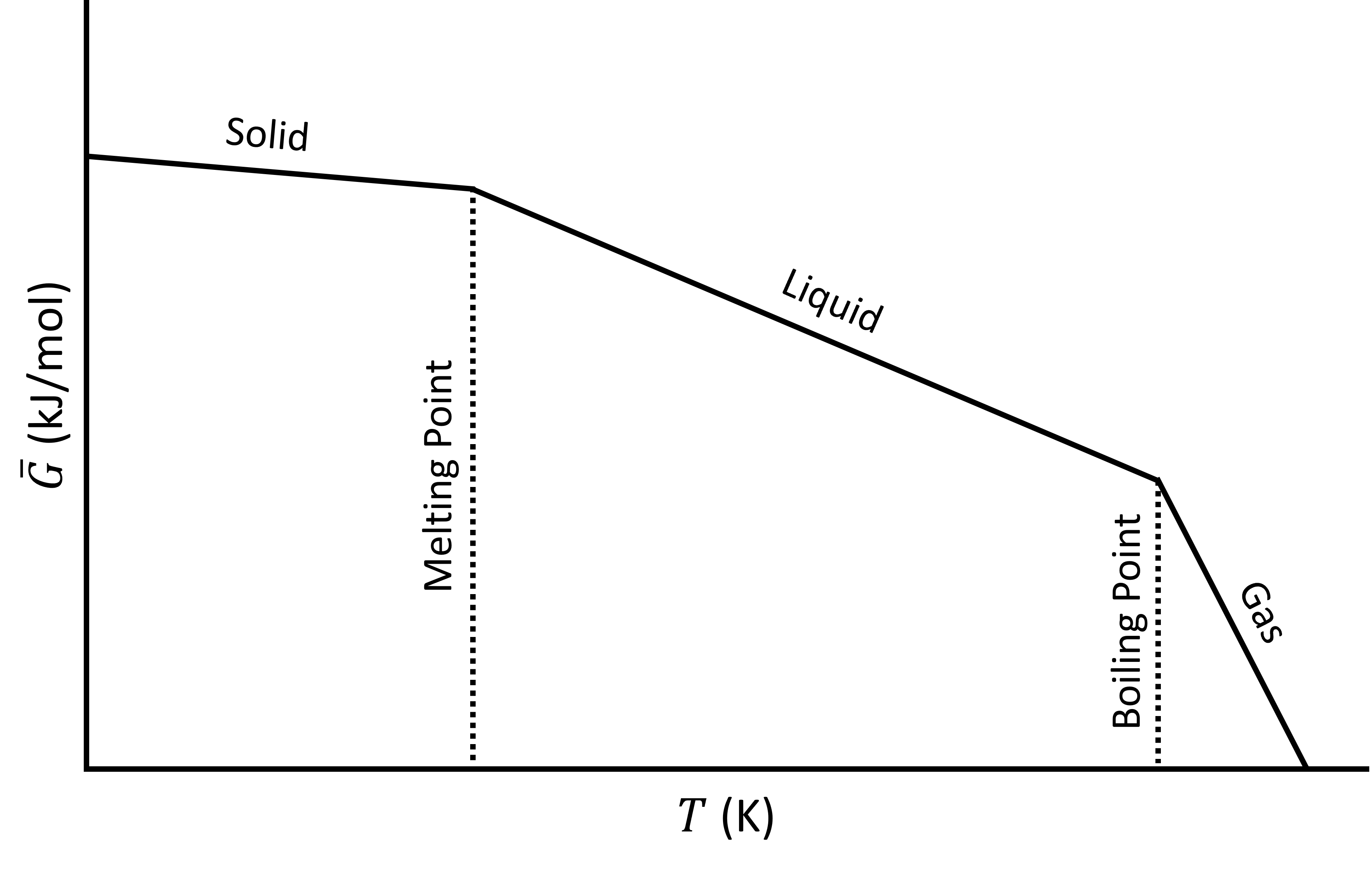
Energía Gibbs (\(\bar{G}\)) en función de la temperatura (\(T\)).
Aunque la\(G\) curva es continua, sus derivadas de primer orden (\(-S\)) son discontinuas en los cambios de fase. Es por ello que esta transición llamó una transición de primer orden. Podríamos decir que:
- \(G\)es continuo pero tiene una flexión
- Las derivadas de primer orden (\(H\)\(S\),,..) son discontinuas (tienen un salto)
- Las derivadas de segundo orden (\(C_P\),..) tienen una singularidad (ir a ∞)
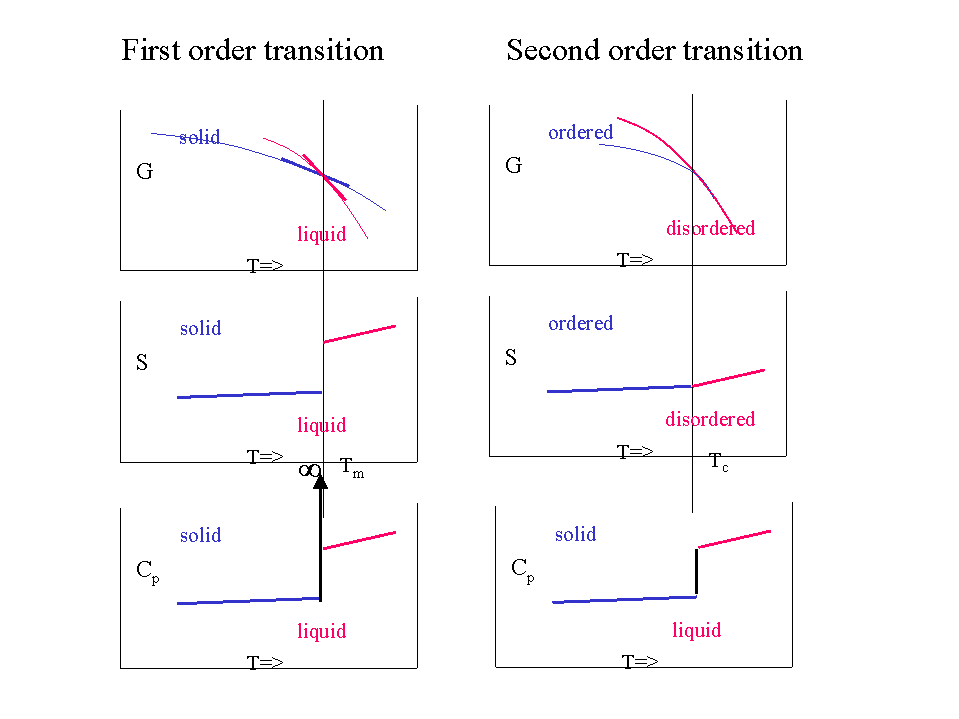
Transiciones de Segundo Orden
Transiciones más sutiles donde\(G\) es continua,\(H\) y también\(S\) son continuas pero tienen una torcedura y la discontinuidad solo se encuentra en las derivadas de segundo orden (tales como\(C_P\)) también existen. Se llaman transiciones de segundo orden. En tal caso:
- \(G\)es continuo y no tiene dobleces
- Las derivadas de primer orden (\(H\),\(S\),..) son continuas (pero tienen una torcedura)
- Las derivadas de segundo orden (\(C_P\),..) son discontinuas (tienen un salto)
| Orden de transición | Función | 1ª Orden | 2º Orden |
|---|---|---|---|
| 0 | G, A | kink | liso |
| 1 | H, S, V,.. | salto | kink |
| 2 | CP, CV, α, κ | cantar. ∞ | salto |
Esta clasificación se remonta a Ehrenfest. Obviamente se basa en la pregunta: ¿qué derivado de orden es el primero en ir discontinuo? Por supuesto que podríamos extender este principio y definir transiciones de tercer orden pero hay razones para dudar de que tales cosas existan. Otro problema es que se supone que el orden debe ser entero: 1,2, etc. ¿Es posible tener una transición de orden no entero intermedio, digamos 1.3? Aunque las derivadas del orden fraccional están más allá del alcance del plan de estudios de química, las matemáticas sí existen (Liouville).
Gibbs Energía Libre y Transiciones de Fase
La energía libre de Gibbs es una función particularmente importante en el estudio de fases y transiciones de fase. El comportamiento de\(G(N, P,T)\), particularmente en función de\(P\) y\(T\), puede significar una transición de fase y puede decirnos algunas de las propiedades termodinámicas de diferentes fases.
Consideremos, primero, el comportamiento de\(G\) vs.\(T\) entre las fases sólida y líquida del benceno: Inmediatamente notamos varias cosas. Primero, aunque la energía libre es continua a través de la transición de fase, su primera derivada, no\(\partial G/\partial T\) es: La pendiente de\(G(T)\) en la región sólida es diferente de la pendiente en la región líquida. Cuando la primera derivada de la energía libre con respecto a una de sus variables termodinámicas dependientes es discontinua a través de una transición de fase, este es un ejemplo de lo que se denomina transición de fase de primer orden. La transición de fase sólido-líquido-gas de la mayoría de las sustancias es de primer orden. Cuando la energía libre exhibe primeras derivadas continuas pero segundas derivadas discontinuas, la transición de fase se denomina segundo orden. Ejemplos de este tipo de transición de fase son la transición orden-trastorno en materiales paramagnéticos.
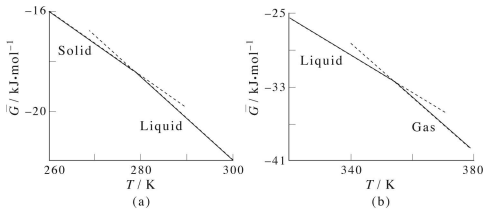
Ahora, recordemos que
\[S = -\dfrac{\partial G}{\partial T} \label{13.1}\]
Considera las pendientes en las partes sólidas y líquidas de la gráfica:
\[\dfrac{\partial G^\text{(solid)}}{\partial T} = -S^\text{(solid)}, \: \: \: \: \: \: \: \dfrac{\partial G^\text{(liquid)}}{\partial T} = -S^\text{(liquid)} \label{13.2}\]
Sin embargo, desde
\[\dfrac{\partial G^\text{(liquid)}}{\partial T} < \dfrac{\partial G^\text{(solid)}}{\partial T} \label{13.3}\]
(tenga en cuenta que las pendientes son todas negativas, y la pendiente de la línea líquida es más negativa que la de la línea continua), se deduce que\(-S^\text{(liquid)} < -S^\text{(solid)}\) or \(S^\text{(liquid)} > S^\text{(solid)}\). This is what we might expect considering that the liquid phase is higher in entropy than the solid phase. The same argument can be made with regards to the gaseous phase.
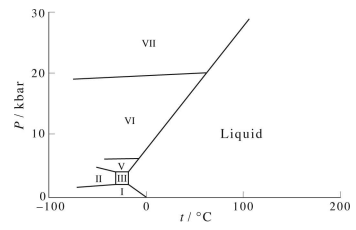
De igual manera, si consideramos la dependencia de\(G\) on pressure, we obtain a curve like that shown in the figure below:
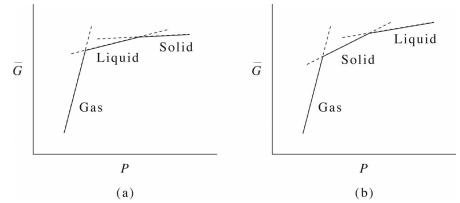
Como se señaló anteriormente, aquí nuevamente, vemos que la primera derivada de\(\bar{G} (P)\) is discontinuous, signifying a first-order phase transition. Recalling that the average molar volume is
\[\bar{V} = \dfrac{\partial \bar{G}}{\partial P} \label{13.4}\]
De la gráfica, vemos que las pendientes obedecen
\[\bar{V}^\text{(gas)} \gg \bar{V}^\text{(liquid)} > \bar{V}^\text{(solid)} \label{13.5}\]
como cabría esperar para una sustancia normal como el benceno a una temperatura por encima de su punto triple. Debido a que la temperatura está por encima del punto triple, la energía libre sigue un camino continuo (aunque no es en todas partes diferenciable) de gas a líquido a sólido.
Por otro lado, para el agua, vemos algo un poco diferente, es decir, que
\[\bar{V}^\text{(gas)} \gg \bar{V}^\text{(solid)} > \bar{V}^\text{(liquid)} \label{13.6}\]
a una temperatura por debajo del punto triple. Esto, nuevamente, indica, la propiedad inusual del agua de que su fase sólida es menos densa que su fase líquida en la región de coexistencia.
Curiosamente, si nos fijamos en cómo la trama de\(G(P)\) changes with \(T\), we obtain a plot like that shown below: Below the triple point, it is easy to see from the benzene phase diagram that the system proceeds directly from solid to gas. There is a liquid curve on this plot that is completely disconnected from the gas-solid curve, suggesting that, below the triple point, the liquid state can exist metastably if at all. AT the triple point, the solid can transition into the liquid or gas phases depending on the value of the free energy. Near the critical temperature, we see the liquid-gas transition line, while the solid line is disconnected. Above the critical temperature, the system exists as a supercritical fluid, which is shown on the lower line, and this line now shows derivative discontinuity.

Variables conjugadas
Como se discutió anteriormente hay muchas otras formas de trabajo posibles, como el trabajo eléctrico, el trabajo magnético o el trabajo elástico. Estos se incorporan comúnmente en el formalismo de la termodinámica al agregar otros términos, por ejemplo:
\[dG = -SdT + VdP + ℰde + MdH + FdL + γdA \nonumber \]
- De significa la fuerza electromotriz y de la cantidad de carga transportada en su contra.
- Mdh significa magnetización y (cambio de) campo magnético.
- F representa la fuerza elástica de, por ejemplo, una banda de goma dL para la longitud en la que se estira
- γ significa la tensión superficial (por ejemplo, de una burbuja de jabón), A por su área de superficie.
Los términos siempre aparecen en un par de lo que se conoce como variables conjugadas. Eso es aún más claro si escribimos la función de estado en lugar de su forma diferencial:
\[G = U + PV -TS + ℰe + MH + FL + γA + ... \nonumber \]
El término PV también puede generalizarse -y necesita serlo- para un par conjugado de fluido viscoso a un par conjugado tensión-deformación. Luego involucra un tensor de estrés. Pronto nos encontraremos con otro par conjugado: μdn que se ocupa de los cambios en la composición (n) y el potencial termodinámico μ.

