29.8: Un Catalizador Afecta el Mecanismo y la Energía de Activación
- Page ID
- 79486
Como puede verse a partir de la ecuación de Arrhenius, la magnitud de la energía de activación\(E_a\), determina el valor de la constante de velocidad,\(k\), a una temperatura dada y por lo tanto la velocidad de reacción general. Los catalizadores proporcionan un medio para reducir\(E_a\) y aumentar la velocidad de reacción. Los catalizadores se definen como sustancias que participan en una reacción química pero que no se cambian ni se consumen. En cambio, proporcionan un nuevo mecanismo para que ocurra una reacción que tiene una energía de activación menor que la de la reacción sin el catalizador.

Catálisis homogénea se refiere a reacciones en las que el catalizador está en solución con al menos uno de los reactivos mientras que la catálisis heterogénea se refiere a reacciones en las que el catalizador está presente en una fase diferente, generalmente como un sólido, a la de los reactivos. La Figura 29.8.1 muestra una comparación de los perfiles de energía de una reacción en ausencia y presencia de un catalizador.
Considerar una reacción elemental no catalizada
\[\text{A} \overset{k}{\longrightarrow} \text{P} \nonumber \]
que procede a\(k\) ritmo a cierta temperatura. La velocidad de reacción se puede expresar como
\[\dfrac{d \left[ \text{A} \right]}{dt} = -k \left[ \text{A} \right] \nonumber \]
En presencia de un catalizador\(\text{C}\), podemos escribir la reacción como
\[\text{A} + \text{C} \overset{k_\text{cat}}{\longrightarrow} \text{P} + \text{C} \nonumber \]
y la velocidad de reacción como
\[\dfrac{d \left[ \text{A} \right]}{dt} = -k \left[ \text{A} \right] - k_\text{cat} \left[ \text{A} \right] \left[ \text{C} \right] \nonumber \]
donde el primer término representa la reacción no catalizada y el segundo término representa la reacción catalizada. Debido a que la velocidad de reacción de la reacción catalizada es a menudo magnitudes mayores que la de la reacción no catalizada (es decir\(k_\text{cat} \gg k\)), el primer término a menudo puede ignorarse.
Ejemplo de Catálisis Homogénea: Catálisis Acida
Un ejemplo común de catalizadores homogéneos son los ácidos y bases. Por ejemplo, dada una reacción global es\(\text{S} \rightarrow \text{P}\). Si\(k\) es la tasa, entonces
\[\dfrac{d \left[ \text{P} \right]}{dt} = k \left[ \text{S} \right] \nonumber \]
El propósito de una enzima es mejorar la tasa de producción del producto\(\text{P}\). Las ecuaciones de la reacción catalizada por ácido son
\[\begin{align} \text{S} + \text{A}H &\overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}} \text{S}H^+ + \text{A}^- \\ \text{S}H^+ + H_2 O &\overset{k_2}{\rightarrow} \text{P} + H_3 O^+ \\ H_3 O^+ + \text{A}^- &\overset{k_3}{\underset{k_{-3}}{\rightleftharpoons}} \text{A}H + H_2 O \end{align} \nonumber \]
El conjunto completo de ecuaciones cinéticas es
\[\begin{align} \dfrac{d \left[ \text{S} \right]}{dt} &= -k_1 \left[ \text{S} \right] \left[ \text{A} H \right] + k_{-1} \left[ \text{S} H^+ \right] \left[ \text{A}^- \right] \\ \dfrac{ d \left[ \text{A} H \right]}{dt} &= -k_1 \left[ \text{S} \right] \left[ \text{A} H \right] + k_{-1} \left[ \text{S} H^+ \right] \left[ \text{A}^- \right] - k_{-3} \left[ \text{A} H \right] + k_3 \left[ H_3 O^+ \right] \left[ \text{A}^- \right] \\ \dfrac{d \left[ \text{S} H^+ \right]}{dt} &= k_1 \left[ \text{S} \right] \left[ \text{A} H \right] - k_{-1} \left[ \text{S} H^+ \right] \left[ \text{A}^- \right] - k_2 \left[ \text{S} H^+ \right] \\ \dfrac{d \left[ \text{A}^- \right]}{dt} &= k_1 \left[ \text{S} \right] \left[ \text{A} H \right] - k_{-1} \left[ \text{S} H^+ \right] \left[ \text{A}^- \right] -k_2 \left[ \text{A}^- \right] \left[ H_3 O^+ \right] + k_{-3} \left[ \text{A} H \right] \\ \dfrac{d \left[ \text{P} \right]}{dt} &= k_2 \left[ \text{S} H^+ \right] \\ \dfrac{d \left[ H_3 O^+ \right]}{dt} &= -k_2 \left[ \text{S} H^+ \right] - k_3 \left[ H_3 O^+ \right] \left[ \text{A}^- \right] + k_{-3} \left[ \text{A} H \right] \end{align} \nonumber \]
No podemos resolverlos fácilmente, ya que son no lineales. No obstante, consideremos dos casos\(k_2 \gg k_{-1} \left[ \text{A}^- \right]\) y\(k_2 \ll k_{-1} \left[ \text{A}^- \right]\). En ambos casos,\(\text{S} H^+\) se consume rápidamente, y podemos aplicar una aproximación de estado estacionario:
\[\dfrac{d \left[ \text{S} H^+ \right]}{dt} = k_1 \left[ \text{S} \right] \left[ \text{A} H \right] - k_{-1} \left[ \text{A}^- \right] \left[ \text{S} H^+ \right] - k_2 \left[ \text{S} H^+ \right] = 0 \nonumber \]
Reorganización en términos de\(\text{S} H^+\) rendimientos
\[\left[ \text{S} H^+ \right] = \dfrac{k_1 \left[ \text{S} \right] \left[ \text{A} H \right]}{k_{-1} \left[ \text{A}^- \right] + k_2} \nonumber \]
y la tasa de producción de\(\text{P}\) puede escribirse como
\[\dfrac{d \left[ \text{P} \right]}{dt} = k_2 \left[ \text{S} H^+ \right] = \dfrac{k_1 k_2 \left[ \text{S} \right] \left[ \text{A} H \right]}{k_{-1} \left[ \text{A}^- \right] + k_2} \nonumber \]
En el caso donde\(k_2 \gg k_{-1} \left[ \text{A}^- \right]\), la Ecuación 29.8.17 puede escribirse como
\[\dfrac{d \left[ \text{P} \right]}{dt} = k_1 \left[ \text{S} \right] \left[ \text{A} H \right] \nonumber \]
que se conoce como reacción general catalizada por ácidos. Por otro lado, si\(k_2 \ll k_{-1} \left[ \text{A}^- \right]\), podemos usar una aproximación de equilibrio para escribir la tasa de producción de\(\text{P}\) como
\[\dfrac{d \left[ \text{P} \right]}{dt} = \dfrac{k_1 k_2 \left[ \text{S} \right] \left[ \text{A} H \right]}{k_{-1} \left[ \text{A}^- \right]} = \dfrac{k_1 k_2}{k_{-1} K} \left[ \text{S} \right] \left[ H^+ \right] \nonumber \]
donde\(K\) es la constante de disociación ácida:
\[K = \dfrac{ \left[ \text{A}^- \right] \left[ H^+ \right]}{\left[ \text{A} H \right]} \nonumber \]
En este caso, la reacción es catalizada por ión hidrógeno.
Ejemplo de Catálisis Heterogénea: Catálisis superficial de reacciones en fase gaseosa
Muchas reacciones en fase gaseosa se catalizan sobre una superficie sólida. Para una reacción unimolecular de primer orden, el mecanismo de reacción puede escribirse como
\[\text{A} \left( g \right) + \text{S} \left( s \right) \overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}} \text{AS} \left( s \right) \nonumber \]
\[\text{AS} \left( s \right) \overset{k_2}{\rightarrow} \text{P} \left( g \right) + \text{S} \left( g \right) \nonumber \]
donde la primera etapa es la adsorción reversible de la molécula de gas\(\text{A}\), sobre sitios activos en la superficie del catalizador\(\text{S}\),, para formar un estado de transición\(\text{AS}\), y la segunda etapa es la conversión de\(\text{A}\) moléculas adsorbidas en especies\(\text{P}\). Aplicando la aproximación de estado estacionario a las especies\(\text{AS}\), podemos escribir
\[\dfrac{d \left[ \text{AS} \right]}{dt} = k_1 \left[ \text{A} \right] \left[ \text{S} \right] - k_{-1} \left[ \text{AS} \right]_{ss} - k_2 \left[ \text{AS} \right]_{ss} = 0 \nonumber \]
Debido a que la concentración de sitios activos totales en la superficie del catalizador se fija en\(\left[ \text{S} \right]_0\), la concentración de especies adsorbidas en la superficie del catalizador, se\(\left[ \text{AS} \right]\) puede escribir como
\[\left[ \text{AS} \right] = \theta \left[ \text{S} \right]_0 \nonumber \]
y\(\left[ \text{S} \right]\) can be written as
\[\left[ \text{S} \right] = \left( 1 - \theta \right) \left[ \text{S} \right]_0 \nonumber \]
donde\(\theta\) is the fractional surface coverage of species \(\text{A}\) on the catalyst surface. We can now write Equation 29.8.23 as
\[k_1 \left[ \text{A} \right] \left( 1 - \theta \right) \left[ \text{S} \right]_0 - \left( k_{-1} + k_2 \right) \theta \left[ \text{S} \right]_0 = 0 \nonumber \]
Reorganizar la ecuación anterior en términos de\(\theta\) yields
\[\theta = \dfrac{k_1 \left[ \text{A} \right]}{k_1 \left[ \text{A} \right] + k_{-1} + k_2} \nonumber \]
La tasa de producción de\(\text{P}\) can be written as
\[\dfrac{d \left[ \text{P} \right]}{dt} = k_2 \left[ \text{AS} \right]_{ss} = k_2 \theta \left[ \text{S} \right]_0 = \dfrac{k_1 k_2}{k_1 \left[ \text{A} \right] + k_{-1} + k_2} \left[ \text{A} \right] \left[ \text{S} \right]_0 \nonumber \]
A partir de la ecuación anterior, podemos observar la importancia de tener altas áreas superficiales para las reacciones catalíticas.
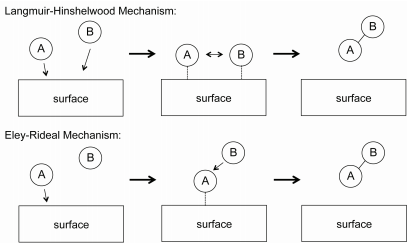
Para las reacciones bimoleculares en fase gaseosa, dos mecanismos de uso general para explicar la cinética de las reacciones son los mecanismos Langmuir-Hinshelwood y Eley-Rideal, mostrados en la Figura 29.8.2 . En el mecanismo Langmuir-Hinshelwood,\(\text{A}\) and \(\text{B}\) both adsorb onto the catalyst surface, at which they react to form a product. The reaction mechanism is
\[\text{A} \left( g \right) + \text{S} \left( s \right) \overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}} \text{AS} \left( s \right) \nonumber \]
\[\text{B} \left( g \right) + \text{S} \left( s \right) \overset{k_2}{\underset{k_{-2}}{\rightleftharpoons}} \text{BS} \left( s \right) \nonumber \]
\[\text{AS} \left( s \right) + \text{BS} \left( s \right) \overset{k_3}{\rightarrow} \text{P} \nonumber \]
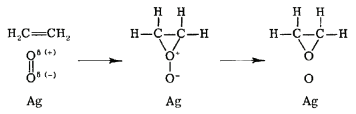
La ley de velocidad para el mecanismo Langmuir-Hinshelwood se puede derivar de manera similar a la de las reacciones catalíticas unimoleculares asumiendo que el número total de sitios activos en la superficie del catalizador es fijo. En el mecanismo Eley-Rideal, solo una especie se adsorbe sobre la superficie del catalizador. Un ejemplo de tal reacción es la oxidación parcial de etileno en óxido de etileno, como se muestra en la Figura 29.8.3 . En esta reacción, el oxígeno diatómico se adsorbe sobre la superficie catalítica donde reacciona con las moléculas de etileno en la fase gaseosa.
Las reacciones para el mecanismo Eley-Rideal pueden escribirse como
\[\text{A} \left( g \right) + \text{S} \left( s \right) \overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}} \text{AS} \left( s \right) \nonumber \]
\[\text{AS} \left( s \right) + \text{B} \left( g \right) \overset{k_2}{\rightarrow} \text{P} \left( g \right) + \text{S} \left( s \right) \nonumber \]
Suponiendo que\(k_{-1} \gg k_1\), we can apply a steady-state approximation to species \(\text{AS}\):
\[\dfrac{d \left[ \text{AS} \right]}{dt} = 0 = k_1 \left[ \text{A} \right] \left[ \text{S} \right] - k_{-1} \left[ \text{AS} \right]_{ss} - k_2 \left[ \text{AS} \right]_{ss} \left[ \text{B} \right] \nonumber \]
Como en el caso de las reacciones catalizadas unimoleculares, podemos expresar las concentraciones de\(\text{AS}\) and \(\text{S}\) in terms of a fraction of the total number of active sites, \(\text{S}_0\) and rewrite the above equation as
\[0 = k_1 \left[ \text{A} \right] \left( 1 - \theta \right) \left[ \text{S} \right]_0 - k_{-1} \left[ \text{S} \right]_0 - k_2 \theta \left[ \text{S} \right]_0 \left[ \text{B} \right] \nonumber \]
Resolviendo para\(\theta\) yields
\[\theta = \dfrac{k_1 \left[ \text{A} \right]}{k_1 \left[ \text{A} \right] + k_{-1} + k_2 \left[ \text{B} \right]} \nonumber \]
Además, si\(k_2 \ll k_1\) and \(k_{-1}\), we can simplify \(\theta\) to
\[\theta = \dfrac{k_1 \left[ \text{A} \right]}{k_1 \left[ \text{A} \right] + k_{-1}} \nonumber \]
La tasa de producción de\(\text{P}\) can be expressed as
\[\dfrac{d \left[ \text{P} \right]}{dt} = k_2 \left[ \text{AS} \right]_{ss} \left[ \text{B} \right] = k_2 \theta \left[ \text{S} \right]_0 \left[ \text{B} \right] = \dfrac{k_1 k_2 \left[ \text{A} \right]}{k_1 \left[ \text{A} \right] + k_{-1}} \left[ \text{S} \right]_0 \left[ \text{B} \right] \nonumber \]
También podemos escribir la expresión anterior en términos de la constante de equilibrio,\(K\), which is equal to\(k_1/k_{-1}\)
\[\dfrac{d \left[ \text{P} \right]}{dt} = K k_2 \left[ \text{B} \right] \dfrac{K \left[ \text{A} \right]}{K \left[ \text{A} \right] + 1} \nonumber \]

