6.3: La aproximación Hartree-Fock

Desafortunadamente, la aproximación de Hartree ignora una propiedad importante de las funciones de onda electrónicas: su antisimetría permutacional. El Hamiltoniano electrónico completo

\[H = \sum_j {- \dfrac{\hbar^2}{2m} \nabla^2_j - \dfrac{Ze^2}{r_j}} + \dfrac{1}{2} \sum_j^k \dfrac{e^2}{|r_j-r_k|}\label{6.1.13}\nonumber \]

es invariante (es decir, se deja sin cambios) bajo la operación\(P_{i,j}\) en la que un par de electrones tienen sus etiquetas (i, j) permutadas. Decimos que\(H\) conmuta con el operador de permutación\(P_{i,j}\). Este hecho implica que cualquier solución\(\psi\) a\(H\psi = E\psi\) debe ser también una función propia de\(P_{i,j}\) Porque los operadores de permutación son idempotentes, lo que significa que si uno aplica\(P_{i,j}\) dos veces, se obtiene la identidad\(PP=1\), se puede ver que los valores propios de\(P_{i,j}\) must ser cualquiera\(+1\) o\( –1\). Es decir, si\(P \psi=c\psi\), entonces\(P P \psi = cc \psi\), pero\(PP=1\) significa eso\(cc = 1\), así\(c = +1\) o\(–1\).

Como resultado del\(H\) desplazamiento con operadores de permutación de electrones y de la idempotencia de\(P\), las funciones propias\(\psi\) deben ser impares o pares bajo la aplicación de dicha permutación. Las partículas cuyas funciones de onda son pares por debajo\(P\) se llaman partículas de Bose o Bosones; aquellas para las cuales\(\psi\) es impar se llaman Fermiones. Los electrones pertenecen a esta última clase de partículas.

La función de producto spin-orbital simple utilizada en la teoría de Hartree

\[\psi= ​\prod_{k=1}^N \phi_k\label{6.1.14}\nonumber \]

no tiene la simetría permutacional adecuada. Por ejemplo, la función Be atom

\[\psi = 1s\alpha(1) 1s\beta(2) 2s\alpha(3) 2s\beta(4) \label{6.1.15}\nonumber \]

no es impar bajo el intercambio de las etiquetas de los electrones 3 y 4; en cambio se obtiene

\[P_{3,4} \psi = 1s\alpha(1) 1s\beta(2) 2s\alpha(4) 2s\beta(3) \nonumber\]

Sin embargo, tales productos de los orbitales de espín (es decir, orbitales multiplicados por\(a\) o funciones de\(b\) espín) pueden convertirse en funciones propiamente antisimétricas formando el determinante de una\(N \times N\) matriz cuyo índice de fila marca el orbital de espín y cuyo índice de columna marca el electrón. Por ejemplo, la función Be atom\(1s\alpha(1) 1s\beta(2) 2s\alpha(3) 2s\beta(4)\) produce la\(4 \times 4\) matriz cuyo determinante se muestra a continuación

\ [\ izquierda|\ begin {array} {cccc}
1s\ alfa (1) y 1s\ alfa (2) y 1s\ alfa (3) y 1s\ alfa (4)\\
1s\ beta (1) y 1s\ beta (2) y 1s\ beta (3) y 1s\ beta (4)\\
2s\ alfa (1) y 2s\ alfa (2) y 2s\ alfa (3) y 2s\ alfa (4)\\
2s\ beta (1) y 2s\ beta (2 ) & 2s\ beta (3) & 2s\ beta (4)
\ end {array}\ derecha|
\ nonumber\]

Claramente, si se intercambiara alguna columna de este determinante, se cambia el signo de la función. Además, si un determinante contiene dos o más filas que son idénticas (es decir, si se intenta formar tal función teniendo dos o más orbitales giratorios iguales), se desvanece. Es así como tales funciones de onda antisimétricas encarnan el principio de exclusión de Pauli.

Una forma conveniente de escribir tal determinante es la siguiente:

\[\sum_P (-1)^p \phi_{P1} (1) \phi_{P2}(2) … \phi_{PN}(N),\nonumber \]

donde la suma es sobre todo N! permutaciones de los\(N\) orbitales de giro y la notación\((-1)^p\) significa que un —1 se fija a cualquier permutación que implique un número impar de intercambios por pares de orbitales espín-orbitales y se le da un signo +1 a cualquiera que involucre un número par. Para normalizar adecuadamente tal función de onda determinental, hay que multiplicarla por\(\dfrac{1}{\sqrt{N!}}\). Entonces, el resultado final es que una ondafunción de la forma

\[\psi = \frac{1}{\sqrt{N!}} \sum_P (-1)^p \phi_{P1} (1) \phi_{P2}(2) … \phi_{PN}(N),\label{6.1.16}\nonumber \]

que a menudo se escribe en notación corta como,

\[\psi = |\phi_1 (1) \phi_2(2) … \phi_N(N)|\label{6.1.17}\nonumber \]

tiene la antisimetría permutacional adecuada. Obsérvese que tales funciones consisten en como suma de\(N!\) factores, todos los cuales tienen exactamente el mismo número de electrones que ocupan los mismos espín-orbitales; la única diferencia entre los\(N!\) términos implica qué electrón ocupa qué spin-orbital. Por ejemplo, en la\(1s\alpha 2s\alpha\) función apropiada al estado excitado de Él, se tiene

\[\psi = \frac{1}{\sqrt{2}} \{1s\alpha(1) 2s\alpha(2) – 2s\alpha(1) 1s\alpha(2)\} \label{6.1.18}\nonumber \]

Esta función es claramente impar bajo el intercambio de las etiquetas de los dos electrones, sin embargo cada uno de sus dos componentes tiene un electrón es un\(1s\alpha\) spin-orbital y otro electrón en un\(2s\alpha\) spin-orbital.

Si bien tener que hacer\(\psi\) antisimétrico parece complicar las cosas significativamente, resulta que la ecuación de Schrödinger apropiada a los orbitales de giro en una función de onda de producto tan antisimetrica es casi la misma que la ecuación de Hartree Schrödnger tratada anteriormente. De hecho, si se minimiza variacionalmente el valor de expectativa del\(N\) -electrón Hamiltoniano para la función de onda del producto antisimétrico anterior sujeto a la condición de que los orbitales espín sean ortonormales

\[\langle\phi_J(r)| \phi_k(r)\rangle = \delta_{J,K} \label{6.1.19}\nonumber \]

se obtiene la siguiente ecuación para el óptimo\({\phi_J(r)}\):

\[h_e \phi_J = \left[– \dfrac{\hbar^2}{2m} \nabla^2 -\dfrac{Ze^2}{r} + \sum_K \langle\phi_K(r’) | \dfrac{e^2}{|r-r’|} | \phi_K(r’)\rangle \right] \phi_J(r)\label{6.1.20}\nonumber \]

\[- \sum_K \langle\phi_K(r’) |\dfrac{e^2}{|r-r’|} | \phi_J(r’)\rangle \phi_K(r) = \epsilon_J \phi_J(r).\label{6.21}\nonumber \]

En esta expresión, que se conoce como la ecuación de Hartree-Fock, ocurren los mismos potenciales de atracción cinética y nuclear que en la ecuación de Hartree. Además, el mismo potencial de Coulomb

\[\sum_K \int \phi_K(r’) \dfrac{e^2}{|r-r’|} \phi_K(r’) dr’ = \sum_K \langle\phi_K(r’)|\dfrac{e^2}{|r-r’|} |\phi_K(r’)\rangle = \sum_K J_K (r)\label{6.1.22}\nonumber \]

aparece. Sin embargo, también se encuentra una llamada contribución de intercambio al potencial de Hartree-Fock que es igual a

\[\sum_L \langle\phi_L(r’) |\dfrac{e^2}{|r-r’|} | \phi_J(r’)\rangle \phi_L(r) \nonumber\]

y a menudo se escribe en notación de mano corta como\(\sum_L K_L \phi_J(r)\). Observe que los términos de Coulomb y de intercambio se cancelan para el\(L=J\) caso; esto hace que el término de autointeracción artificial\(J_L \phi_L(r) \) que puede aparecer en las ecuaciones de Hartree (a menos que uno lo elimine explícitamente) se cancele automáticamente con el término de intercambio\(K_L \phi_L(r)\) en las ecuaciones de Hartree-Fock.

Para derivar las ecuaciones de Hartree-Fock anteriores, se debe hacer uso de las llamadas reglas Slater-Condon para expresar el valor de expectativa hamiltoniana como

\ [\ langle|\ phi_1 (1)\ phi_2 (2)\ cdots\ phi_ {N-1}\ phi_n (N) |H|\ phi_1 (1)\ phi_2 (2)\ cdots\ phi_ {N-1}\ phi_n (N) |\ rangle =\ sum_ {j=1} ^N\ langle\ phi_j (r) |-\ frac {1} {2}\ nabla^2-\ frac {e^2} {r} |\ phi_j (r)\ rangle\\ +\ frac {1} {2}\ sum_ {j, k=1} ^N\ left [\ langle\ phi_j (r)\ phi_k (r') |\ frac {e^2} {|r'|} |\ phi_j (r)\ phi_k (r')\ rangle
-\ langle\ phi_j (r)\ phi_k (r') |\ frac {e^2} {|r-r'|} |\ phi_k (r)\ phi_j (r')\ rangle\ derecha]\ nonumber\]

Este valor de expectativa es una suma de términos (la energía cinética y los potenciales de Coulomb electrón-nuclear) que varían cuadráticamente en los orbitales espín-orbitales (es decir, as\(\langle \phi| {\rm operator} |\phi\rangle\)) más otra suma (los términos de interacción Coulomb e intercambio electrón-electrón) que dependen de la cuarta potencia de los orbitales espín (es decir, como \(\langle \phi\phi |{\rm operator} |\phi\phi \rangle\). Cuando estos términos se diferencian para minimizar el valor de expectativa, generan factores que escalan linealmente y con el tercer poder de los spin-orbitales. Estos son los factores

\[{-\dfrac{\hbar^2}{2m} \nabla^2 -\frac{Z_e^2}{r} } \phi_J(r)\nonumber \]y\[\sum_K \langle\phi_K(r’) |\frac{e^2}{|r-r’|} | \phi_K(r’)\rangle \phi_J(r) - \sum_K \langle \phi_K(r’) |\frac{e^2}{|r-r’|} | \phi_J(r’)\rangle \phi_K(r) \label{6.1.23}\]

que aparecen en las ecuaciones de Hartree-Fock mostradas anteriormente.

Cuando la expansión LCAO de cada espín-orbital de Hartree-Fock (HF) se sustituye en la ecuación de HF Schrödinger anterior, se obtiene de nuevo una ecuación matricial:

\[\sum_\mu \langle\chi_\nu |h_e| \chi_\mu\rangle C_{J,\mu} = \epsilon_J \sum_\mu \langle\chi_\nu|\chi_\mu\rangle C_{J,\mu}\label{6.1.24}\nonumber \]

donde la integral de superposición\(\langle\chi_\nu|\chi_\mu\rangle\) es como se definió anteriormente, y el elemento de\(h_e\) matriz es

\[\langle\chi_\nu| h_e| \chi_\mu\rangle = \langle\chi_\nu| -\dfrac{\hbar^2}{2m} \nabla^2 |\chi_\mu\rangle + \langle\chi_\nu| -\frac{Ze^2}{r} |\chi_\mu\rangle \label{6.1.25}\]

\[+ \sum_{K,\eta,\gamma} C_{K,\eta} C_{K,\gamma} [\langle\chi_\nu(r) \chi_\eta(r’) |\frac{e^2}{|r-r’|} | \chi_\mu(r) \chi_\gamma(r’)\rangle - \langle\chi_\nu(r) \chi_\eta(r’) |\frac{e^2}{|r-r’|} | \chi_\gamma(r) \chi_\mu (r’)\rangle].\label{6.1.26}\]

Claramente, la única diferencia entre esta expresión y el resultado correspondiente de la teoría de Hartree es la presencia del último término, la integral de intercambio. El procedimiento iterativo SCF utilizado para resolver las ecuaciones de Hartree se utiliza nuevamente para resolver las ecuaciones de HF.

Es útil reflexionar sobre el significado físico del Coulomb e intercambiar interacciones entre pares de orbitales. Por ejemplo, el Coulomb integral

\[ J_{1,2} = \int |\phi_1(r)|^2 \frac{e^2}{|r-r’|} |\phi_2(r’)|^2 dr dr’ \label{6.1.27}\nonumber \]

apropiado a los dos orbitales mostrados en la Figura 6.1.3 representa la energía de repulsión coulómbica\(\dfrac{e^2}{|r-r’|}\) de dos densidades de carga\(|\phi_2|^2\),\(|\phi_1|^2\) y, integrada en todas las ubicaciones\(r\) y\(r’\) de los dos electrones.

Figura 6.1.3: Una s y una p Orbital y su Región de Superposición

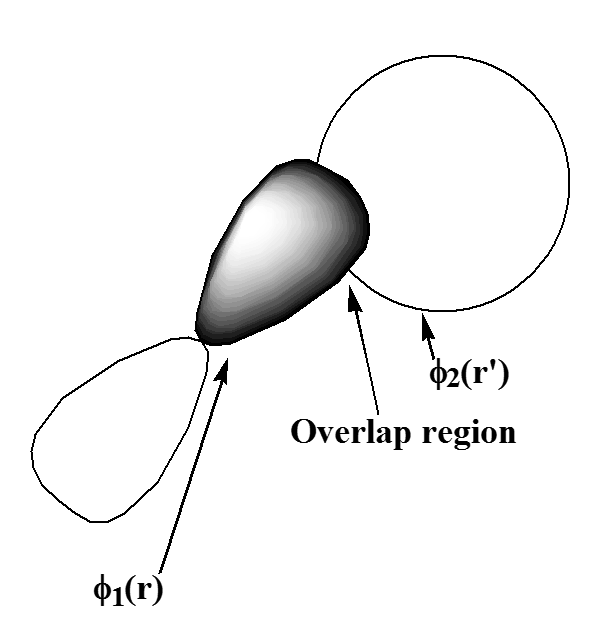
En contraste, el intercambio integral

\[K_{1,2} = \int \phi_1(r) \phi_2(r’) \frac{e^2}{|r-r’|} \phi_2(r) \phi_1(r’) dr dr’\label{6.1.28}\nonumber \]

puede pensarse como la repulsión coulómbica entre dos electrones cuyas coordenadas\(r\) y\(r’\) están ambas distribuidas a lo largo de la “región de superposición”\(\phi_1\)\(\phi_2\). Esta región de superposición es donde ambos\(\phi_1\) y\(\phi_2\) tienen una magnitud apreciable, por lo que las integrales de intercambio tienden a ser significativas en magnitud solo cuando los dos orbitales involucrados tienen regiones sustanciales de superposición.

Finalmente, algunas palabras están en orden sobre una de las partes que más tiempo consumen computadora de cualquier cálculo de Hartree-Fock (o las que se discuten más adelante): la tarea de evaluar y transformar las integrales de dos electrones

\[\langle\chi_\nu(r) \chi_\eta(r’) |\frac{e^2}{|r-r’|} | \chi_\mu(r) \chi_\gamma(r’)\rangle.\label{6.1.29}\nonumber \]

Cuando se utilizan M GTO como funciones básicas, la evaluación\(\dfrac{M^4}{8}\) de estas integrales a menudo plantea un obstáculo importante. Por ejemplo, con 500 orbitales base, habrá del orden de 7.8 x10 ⁹ tales integrales. Con cada integral requiriendo 2 palabras de almacenamiento en disco (la mayoría de las integrales deben evaluarse con doble precisión), esto requeriría al menos 1.5 x10 ⁴ Mwords de almacenamiento en disco. Incluso en la era de las computadoras modernas que poseen 500 discos Gby, este es un requisito significativo. Uno de los avances técnicos más importantes que se encuentra bajo mucho desarrollo actual es el cálculo eficiente de tales integrales cuando el producto funciona\(\chi_\nu(r) \chi_\mu(r)\) y\(\chi_\gamma(r’) \chi_\eta(r’)\) que muestran la dependencia de las coordenadas r y r' de los dos electrones están espacialmente distantes. En particular, las llamadas expansiones multipolares de estas funciones de producto se utilizan para obtener aproximaciones más eficientes a sus integrales cuando estas funciones están muy separadas. Además, tales expansiones ofrecen una manera confiable de ignorar (es decir, aproximarse como cero) muchas integrales cuyas funciones de producto están suficientemente distantes. Tales enfoques muestran una promesa considerable para reducir la lista integral de\(\dfrac{M^4}{8}\) dos electrones a una cuyo tamaño se escala mucho menos fuertemente con el tamaño de la base AO y forman un componente importante si los esfuerzos para lograr necesidades de CPU y almacenamiento que escalen linealmente con el tamaño de la molécula.

Teorema de Koopman

Las ecuaciones HF-SCF\(h_e \phi_i = \epsilon_i \phi_i\) implican que las energías orbitales\(\epsilon_i\) pueden escribirse como:

\[\epsilon_i = \langle \phi_i | h_e | \phi_i \rangle = \langle \phi_i | T + V | \phi_i \rangle + \sum_{j({\rm occupied})} \langle \phi_i | J_j - K_j | \phi_i \rangle \nonumber \]

\[= \langle \phi_i | T + V | \phi_i \rangle + \sum_{j({\rm occupied})} [ J_{i,j} - K_{i,j} ],\label{6.1.30}\nonumber \]

donde\(T + V\) representa las energías cinética (\(T\)) y de atracción nuclear (\(V\)), respectivamente. Así,\(\epsilon_i\) es el valor promedio de la energía cinética más la atracción coulómbica a los núcleos para un electrón in\(\phi_i\) más la suma sobre todos los espín-orbitales ocupados en\(\psi\) de Coulomb menos Interacciones de intercambio de estos electrones con el electrón adentro\(\phi_i\).

Si\(\phi_i\) es un spin-orbital ocupado, el\(j = i\) término\([ J_{i,i} - K_{i,i}]\) desaparece en la suma anterior y los términos restantes en la suma representan la interacción de Coulomb menos intercambio de\(\phi_i\) con todos los\(N-1\) demás orbitales espín-orbitales ocupados. Si\(\phi_i\) es un spin-orbital virtual, esta cancelación no ocurre porque la suma sobre\(j\) no incluye\(j = i\). Entonces, se obtiene la interacción de intercambio de Coulomb menos\(\phi_i\) con todos\(N\) los orbitales spin-orbitales ocupados en\(\psi\). De ahí que las energías de los orbitales ocupados pertenezcan a interacciones apropiadas a un total de\(N\) electrones, mientras que las energías de los orbitales virtuales pertenecen a un sistema con\(N+1\) electrones. Esta diferencia es muy importante de entender y de tener en cuenta.

Consideremos el siguiente modelo del desprendimiento o unión de un electrón en un sistema\(N\) -electrón.

1. En este modelo, tanto la molécula parental como las especies generadas por la adición o eliminación de un electrón se tratan a nivel de determinante único.
2. Los orbitales Hartree-Fock de la molécula parental se utilizan para describir ambas especies. Se dice que dicho modelo descuida la relajación orbital (es decir, la reoptimización de los orbitales espín para permitirles llegar a ser apropiados a la especie hija).

Dentro de este modelo, la diferencia de energía entre el hijo y el padre se puede escribir de la siguiente manera (\(\phi_k\)representa el spin-orbital particular que se agrega o elimina):

para desprendimiento de electrones:

\[E_{N-1} - E_N = - \epsilon_k \label{6.1.31}\nonumber \]

y para la unión de electrones:

\[E_N - E_{N+1} = - \epsilon_k .\label{6.1.32}\nonumber \]

Derivamos este resultado para el caso en el que se agrega un electrón al\(N+1^{st}\) spin-orbital. Nuevamente, utilizando las reglas de Slater-Condon de la Sección 6.1.2 de este Capítulo, la energía del determinante\(N\) -electrón con espín-orbitales\(\phi_1\) a través de\(f_N\) ocupado es

\[E_N = \sum_{i=1}^N \langle \phi_i | T + V | \phi_i \rangle + \sum_{i=1}^{N} [ J_{i,j} - K_{i,j} ],\label{6.1.33}\nonumber \]

que también se puede escribir como

\[E_N = \sum_{i=1}^N \langle \phi_i | T + V | \phi_i \rangle + \frac{1}{2} \sum_{i,j=1}^{N} [ J_{i,j} - K_{i,j} ].\label{6.1.34}\nonumber \]

Asimismo, la energía\(N+1\) de la función de onda determinante de electrones es

\[E_{N+1} = \sum_{i=1}^{N+1} \langle \phi_i | T + V | \phi_i \rangle + \frac{1}{2} \sum_{i,j=1}^{N+1} [ J_{i,j} - K_{i,j} ].\label{6.1.35}\nonumber \]

La diferencia entre estas dos energías viene dada por

\[E_{N} – E_{N+1} = - \langle \phi_{N+1} | T + V | \phi_{N+1} \rangle - \frac{1}{2} \sum_{i=1}^{N+1} [ J_{i,N+1} - K_{i,N+1} ]\label{6.1.36}\nonumber \]

\[- \frac{1}{2} \sum_{j=1}^{N+1} [ J_{N+1,j} - K_{N+1,j} ] = - \langle \phi_{N+1} | T + V | \phi_{N+1} \rangle - \sum_{i=1}^{N+1} [ J_{i,N+1} - K_{i,N+1} ]\label{6.1.37}\nonumber \]

\[= - \epsilon_{N+1}.\label{6.1.38}\nonumber \]

Es decir, la diferencia de energía es igual a menos la expresión para la energía del\(N+1^{st}\) spin-orbital, que se dio antes.

Entonces, dentro de las limitaciones del HF, modelo orbital congelado, los potenciales de ionización (IPs) y las afinidades electrónicas (EA) se dan como el negativo de las energías spin-orbitales ocupadas y virtuales, respectivamente. Esta afirmación se conoce como el teorema de Koopman; se usa ampliamente en cálculos químicos cuánticos como medio para estimar IPs y EA y a menudo arroja resultados que son cualitativamente correctos (es decir, ± 0.5 eV).

Energías orbitales y la energía total

La energía electrónica total de HF-SCF se puede escribir como:

\[E = \sum_{i({\rm occupied})} \langle \phi_i | T + V | \phi_i \rangle + \sum_{i>j_{({\rm occupied})}} [ J_{i,j} - K_{i,j} ] \label{6.1.39}\nonumber \]

y la suma de las energías orbitales de los spin-orbitales ocupados viene dada por:

\[\sum_{i({\rm occupied})} \epsilon_i = \sum_{i({\rm occupied})} \langle \phi_i | T + V | \phi_i \rangle + \sum_{i,j({\rm occupied})} [J_{i,j} - K_{i,j} ]. \label{6.1.40}\nonumber \]

Estas dos expresiones difieren de una manera muy importante; la suma de energías orbitales ocupadas cuenta dos veces las energías de interacción de Coulomb menos intercambio. Así, dentro de la aproximación Hartree-Fock, la suma de las energías orbitales ocupadas no es igual a la energía total. Este hallazgo nos enseña que no podemos pensar en la energía electrónica total de una ocupación orbital dada solo en términos de las energías orbitales. También necesitamos hacer un seguimiento de las energías de Coulomb e Intercambio entre electrones.