6.4: Deficiencias en el Modelo de Determinante Único
- Page ID
- 71067
Para lograr una precisión química razonable (por ejemplo, ± 5 kcal/mol en EA o IPs o energías de enlace) en los cálculos de estructuras electrónicas, no se puede describir la función de onda\(\psi\) en términos de un solo determinante. La razón por la cual tal función de onda es inadecuada es porque las funciones de densidad de probabilidad espacial no están correlacionadas. Esto significa que la probabilidad de encontrar un electrón en la posición r es independiente de donde estén los otros electrones, lo cual es absurdo porque la repulsión mutua de Coulomb de los electrones hace que se eviten entre sí. Esta evitación mutua es lo que llamamos correlación electrónica porque los movimientos de los electrones, reflejados en sus densidades de probabilidad espacial, están correlacionados (es decir, interrelacionados). Consideremos un ejemplo sencillo para ilustrar este problema con funciones determinantes únicas. El\(|1s\alpha(r) 1s\beta(r’)|\) determinante, cuando se escribe como
\[|1s\alpha(r) 1s\beta(r’)| = \frac{1}{\sqrt{2}}\{1s\alpha(r) 1s\beta(r’) - 1s\alpha(r’) 1s\beta(r)\} \]
puede multiplicarse por sí mismo para producir la densidad de probabilidad espacial y de espín de 2 electrones:
\[P(r, r’) = \frac{1}{2}\{[1s\alpha(r) 1s\beta(r’)]^2 + [1s\alpha(r’) 1s\beta(r)]^2 -1s\alpha(r) 1s\beta(r’) 1s\alpha(r’) 1s\beta(r) - 1s\alpha(r’) 1s\beta(r) 1s\alpha(r) 1s\beta(r’)\}.\]
Si ahora integramos sobre los espines de los dos electrones y hacemos uso de
\[\langle a|a \rangle = \langle b|b \rangle = 1 \label{6.1.1a}\]
y
\[\langle a|b \rangle = \langle b|a\rangle = 0 \label{6.1.1b}\]
obtenemos la siguiente densidad de probabilidad espacial (es decir, con espín ausente):
\[P(r,r’) = |1s(r)|^2 |1s(r’)|^2. \]
Esta probabilidad, al ser producto de la densidad de probabilidad para encontrar un electrón a r veces la densidad de encontrar otro electrón en\(r’\), claramente no tiene correlación en ella. Es decir, la probabilidad de encontrar un electrón en r no depende de donde esté\((r’)\) el otro electrón. Esta forma de producto para\(P(r,r’)\) es un resultado directo de la forma de determinante único para y, por lo que esta forma debe ser incorrecta si se va a tener en cuenta la correlación de electrones.
Correlación de electrones
Ahora, debemos preguntarnos cómo se\(\psi\) debe escribir si se van a tener en cuenta los efectos de correlación electrónica. Como ahora demostramos, resulta que uno puede explicar la evitación de electrones tomando\(\psi\) como una combinación de dos o más determinantes que difieren por la promoción de dos electrones de un orbital a otro orbital. Por ejemplo, al describir el par de electrones de\(\pi^2\) enlace de una olefina o el par de\(ns^2\) electrones en átomos alcalinotérreos, se mezcla en determinantes doblemente excitados de la forma\((\pi^*)^2\) o\(np^2\), respectivamente.
Brevemente, la importancia física de tales determinantes doblemente excitados puede aclararse usando la siguiente identidad que involucra determinantes:
\[C_1 | ..\phi_\alpha \phi_\beta..| - C_2 | ..\phi'_\alpha \phi'_\beta..|\]
\[= \dfrac{C_1}{2} { | ..( \phi - x\phi')\alpha ( \phi + x\phi')b..| - | ..( \phi - x\phi')\beta ( \phi + x\phi')\alpha..| },\]
donde
\[x = \sqrt{\dfrac{C_2}{C_1}} .\]
Esta identidad es importante de entender, así que por favor asegúrate de poder trabajar a través del álgebra necesaria para probarla. Permite interpretar la combinación de dos determinantes que difieren entre sí por una doble promoción de un orbital\((\phi)\) a otro\((\phi')\) como equivalente a un acoplamiento singlete (es decir, que tiene función de\(\alpha\beta-\beta\alpha\) espín) de dos orbitales diferentes\((\phi - x\phi')\) y\((\phi + x\phi')\) que comprenden lo que se llama pares orbitales polarizados. En la realización más simple de dicha descripción de interacción de configuración (CI) de correlación electrónica, cada par de electrones en el átomo o molécula se correlaciona mezclando en una función de estado de configuración (CSF) en la que ese par de electrones se excita doblemente a un orbital correlacionado. Un CSF es la combinación mínima de determinantes necesarios para expresar la función propia de espín adecuada para una ocupación orbital dada.
En el ejemplo de olefina mencionado anteriormente, los dos pares orbitales polarizados no ortogonales implican mezclar los orbitales p y p* para producir dos orbitales polarizados izquierda-derecha como se representa en la Figura 6.1.9:

En este caso, se dice que el par de\(\pi^2\) electrones experimenta correlación izquierda-derecha cuando el\((\pi^*)^2\) determinante se mezcla en la función de onda CI.
En el caso del átomo alcalinotérreo, los pares orbitales polarizados se forman mezclando los\(np\) orbitales\(ns\) y (en realidad, se deben mezclar en cantidades iguales de\(p_x, p_y\), y\(p_z\) orbitales para preservar la\(^1S\) simetría general en este caso), y dar lugar a la correlación angular del electrón par. Tal par de orbitales polarizados se muestra en la Figura 6.1.10.
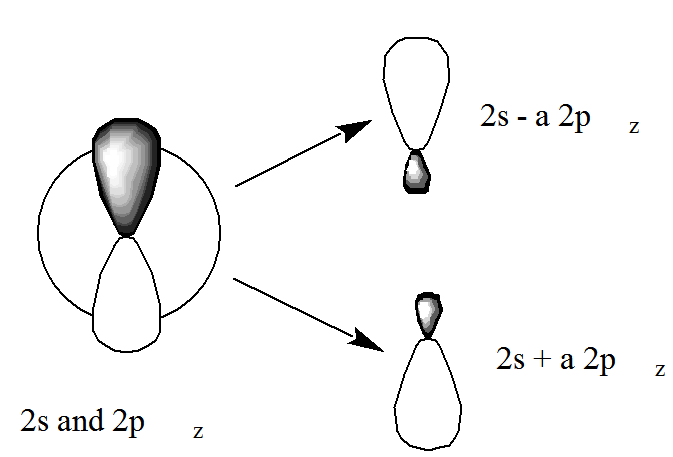
Más específicamente, se encuentra que los siguientes cuatro determinantes tienen las amplitudes más grandes en\(\psi\) para Be:
\[\psi \cong C_1 |1s^22s^2 | - C_2 [|1s^22p_x^2 | +|1s^22p_y^2 | +|1s^22p_z^2 |].\]
El hecho de que estos tres últimos términos posean la misma amplitud\(C_2\) es resultado del requisito de que se desea un estado de\(^1S\) simetría. Se puede demostrar que esta función es equivalente a:
\ [\ psi\ cong\ frac {1} {6} C_1 |1s\ alfa1s\ beta [[(2s-a2p_x)\ alfa (2s+a2p_x)\ beta - (2s-a2p_x)\ beta (2s+a2p_x)\ alfa]\
+ [(2s-a2p_y)\ alfa (2s+a2p_y)\ beta - (2s-a2p_y)\ beta (2s+a2p_y)\ alfa]\\
+ [(2s-a2p_z)\ alfa (2s+a2p_z)\ beta - (2s-a2p_z)\ beta (2s+a2p_z)\ alfa]] |,\]
donde\(a = \sqrt{3C_2/C_1}\).
Aquí dos electrones ocupan el\(1s\) orbital (con opuestos,\(\alpha\) y\(\beta\) espines), y así no están siendo tratados de manera correlacionada, mientras que el otro par reside en orbitales\(2s\)/\(2p\)polarizados de una manera que correlaciona instantáneamente sus movimientos. Estos pares orbitales polarizados\((2s ± a 2p_{x,y,\text{ or }z})\) se forman combinando el\(2s\) orbital con el\(2p_{x,y,\text{ or }z}\) orbital en una proporción determinada por\(C_2/C_1\).
Esta relación se\(C_2/C_1\) puede mostrar usando la teoría de perturbación como proporcional a la magnitud del elemento de la\(\langle 1s^22s^2 |H|1s^22p^2 \rangle\) matriz de acoplamiento entre las dos configuraciones involucradas e inversamente proporcional a la diferencia de energía
\([\langle 1s^22s^2H|1s^22s^2 \rangle - \langle 1s^22p^2|H|1s^22p^2 \rangle]\)
entre estas configuraciones. En general, las configuraciones que tienen valores similares de expectativa hamiltoniana y que están fuertemente acopladas dan lugar a pares orbitales polarizados fuertemente mezclados (es decir, con grandes\(|C_2/C_1|\) proporciones).
II.Más adelante en este Capítulo, aprenderás a evaluar elementos de la matriz hamiltoniana entre pares de funciones de onda antisimétricas. Si estás ansioso por aprender esto ahora, ve a la subsección titulada Las reglas del Slater-Condon y lee eso antes de regresar aquí.
En cada uno de los tres términos equivalentes en la función de onda alcalinotérrea, uno de los electrones de valencia se mueve en un\(2s+a2p\) orbital polarizado en una dirección mientras que el otro electrón de valencia se mueve en el\(2s-a2p\) orbital polarizado en la dirección opuesta. Por ejemplo, el primer término
\([(2s-a2p_x)\alpha(2s+a2p_x)\beta - (2s-a2p_x)\beta(2s+a2p_x)\alpha]\)
describe un electrón que ocupa un orbital\(2s-a2p_x\) polarizado mientras que el otro electrón ocupa el\(2s+a2p_x\) orbital. Los electrones reducen así su repulsión de Coulomb al ocupar diferentes regiones del espacio; en la imagen SCF\(1s^22s^2\), ambos electrones residen en la misma\(2s\) región del espacio. En este ejemplo particular, los electrones experimentan correlación angular para evitarse unos a otros.
El uso de determinantes doblemente excitados se ve así como un mecanismo por el cual\(\psi\) se pueden colocar pares de electrones, que en la imagen de configuración única ocupan el mismo orbital, en diferentes regiones del espacio (es decir, cada uno en un miembro diferente del par orbital polarizado) disminuyendo así su mutua Repulsión de Coulomb. Tales efectos de correlación electrónica son extremadamente importantes para incluir si se espera lograr una precisión químicamente significativa (es decir, ± 5 kcal/mol).
Interacción de configuración esencial
Hay ocasiones en las que la inclusión de dos o más determinantes en\(\psi\) es esencial para obtener incluso una descripción cualitativamente correcta de la estructura electrónica de la molécula. En tales casos, decimos que estamos incluyendo efectos de correlación esenciales. Para ilustrar, consideremos la descripción de los dos electrones en un solo enlace covalente entre dos átomos o fragmentos que etiquetamos X e Y. Los orbitales de fragmentos a partir de los cuales se forman los\(\sigma^*\) MO de enlace\(\sigma\) y antienlace los marcaremos\(s_X\) y\(s_Y\), respectivamente.
Se pueden formar varios determinantes de 2 electrones adaptados a la simetría espacial y de espín (es decir, CSF) colocando dos electrones en los\(\sigma^*\) orbitales\(\sigma\) y. Por ejemplo, para describir el determinante singlete correspondiente a la ocupación\(\sigma^2\) orbital de caparazón cerrado, un solo determinante Slater
\[^1\Sigma (0) = |\sigma\alpha \sigma\beta| = \frac{1}{\sqrt{2}} [\sigma\alpha(1)\sigma\beta(2) - \sigma\beta(1)\sigma\alpha(2) ]\]
basta. Una expresión análoga para el\((\sigma^*)^2\) determinante viene dada por
\[{}^1\Sigma^{**} (0) = | \sigma^*\alpha \sigma^*\beta | = \frac{1}{\sqrt{2}} [ \sigma^*\alpha(1) \sigma^*\beta(2) - \sigma^*\alpha(2) \sigma^*\beta(1) ]\]
Además, el\(M_S = 1\) componente del estado triplete que tiene ocupación\(\sigma\sigma^*\) orbital puede escribirse como un solo determinante de Slater:
\[{}^3\Sigma^{*} (1) = |\sigma\alpha \sigma^*\alpha | = \frac{1}{\sqrt{2}} [\sigma\alpha(1) \sigma^*\alpha(2) - \sigma^*\alpha(1)\sigma\alpha(2) ],\]
al igual que el\(M_S = -1\) componente del estado triplete
\[{}^3\Sigma^{*}(-1) = |\sigma\beta \sigma^*\beta | = \frac{1}{\sqrt{2}} [\sigma\beta(1) \sigma^*\beta(2) - \sigma^*\beta(1)\sigma\beta(2) ].\]
Sin embargo, para describir los estados singlete y\(M_S = 0\) triplete pertenecientes a la\(\sigma\sigma^*\) ocupación, se necesitan dos determinantes:
\[ {}^1\Sigma^{*} (0) = \frac{1}{\sqrt{2}} [\sigma\alpha \sigma^*\beta - \sigma\beta\sigma^*\alpha ]\]
es el singlete y
\[ {}^3\Sigma^{*}(0) = \frac{1}{\sqrt{2}} [\sigma\alpha \sigma^*\beta + \sigma\beta\sigma^*\alpha ] \]
es el triplete (nota, puedes obtener este\(M_S = 0\) triplete aplicando\(\textbf{S}_- = \textbf{S}_- (1) + \textbf{S}_- (2)\) al\(M_S = 1\) triplete). En cada caso, el número cuántico de espín\(S\), su proyección\(M_S\) del eje z y el número\(L\) cuántico se dan en la notación de símbolo de\(^{2S+1}\Lambda(M_S)\) término convencional.
A medida que la distancia\(R\) entre los fragmentos X e Y se cambia desde cerca de su valor de equilibrio\(R_e\) y se acerca al infinito, las energías de\(\sigma^*\) los orbitales\(\sigma\) y varían de una manera bien conocida por los químicos como se representa en la Figura 6.1.11 si X e Y son idénticos.
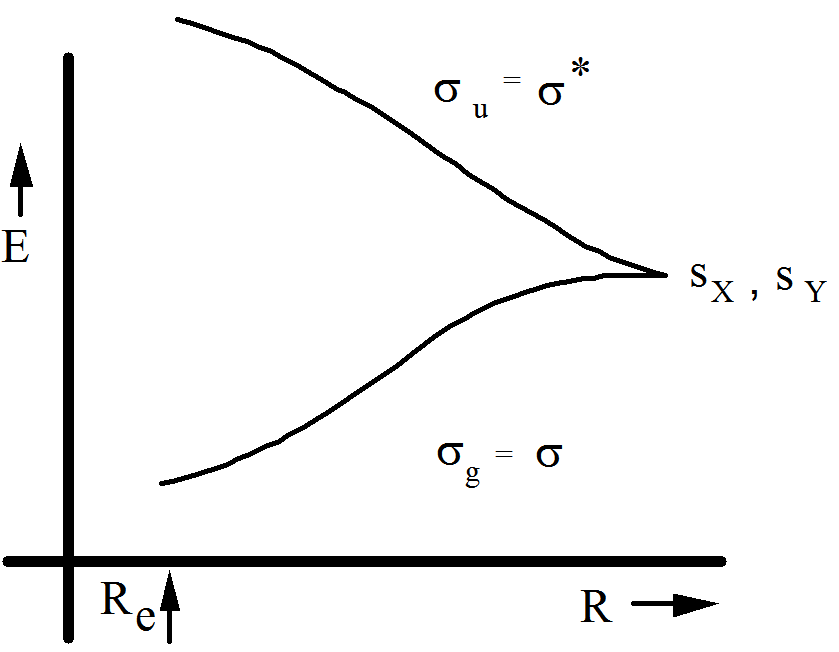
Si X e Y no son idénticos, los\(s_y\) orbitales\(s_x\) y aún se combinan para formar un orbital de unión\(\sigma\) y un\(\sigma^*\) orbital antiadhesión. Las energías de estos orbitales, para valores de R que van de cerca\(R_e\) a\(R\rightarrow \infty\), se representan en la Figura 6.1.12 para el caso en el que X es más electronegativo que Y.
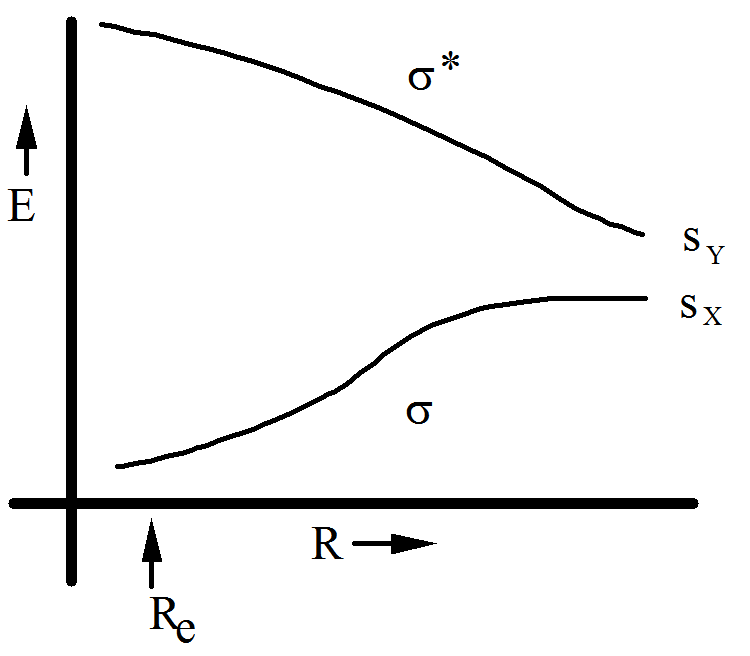
La variación de energía en estas energías orbitales da lugar a variaciones en las energías de los seis determinantes enumerados anteriormente. Como\(R \rightarrow \infty\), las energías de los determinantes son difíciles de intuir porque los\(\sigma^*\) orbitales\(\sigma\) y se degeneran (en el caso homonuclear) o casi así (en el\(X \ne Y\) caso). Para perseguir este punto y llegar a un ordenamiento energético para los determinantes que sea apropiado para la\(R \rightarrow \infty\) región, es útil expresar cada una de esas funciones en términos de los fragmentos orbitales\(s_x \) y\(s_y\) que comprenden\(\sigma\) y\(\sigma^*\). Para ello, las expresiones LCAO-MO para\(\sigma\) y\(\sigma^*\),
\[\sigma = C [s_x + z s_y]\]
y
\[\sigma^* = C^* [z s_x - s_y],\]
se sustituyen en las definiciones determinantes de Slater dadas anteriormente. Aquí\(C\) y\(C^*\) están las constantes de normalización. El parámetro\(z\) es 1.0 en el caso homonuclear y se desvía de 1.0 en relación con la diferencia de energía\(s_x\) y\(s_y\) orbital (si\(s_x\) se encuentra por debajo\(s_y\), entonces\(z < 1.0\); si\(s_x\) se encuentra arriba\(s_y\),\(z > 1.0\)).
Examinemos el\(X=Y\) caso para que el análisis sea lo más sencillo posible. El proceso de sustituir las expresiones anteriores por\(\sigma\) y\(\sigma^*\) en los determinantes Slater que definen las funciones singlete y triplete se puede ilustrar de la siguiente manera para el\(^1\Sigma(0)\) caso:
\[{}^1\Sigma(0) = |\sigma\alpha \sigma\beta| = C_2 | (s_x + s_y) \alpha(s_x + s_y) \beta| \]
\[= C_2 [|s_x \alpha s_x b| + |s_y \alpha s_y \beta| + |s_x \alpha s_y \beta| + |s_y \alpha s_x \beta|] \]
Los dos primeros de estos determinantes de Slater atómico-orbitales (\(|s_x \alpha s_x b|\)y\(|s_y \alpha s_y \beta|\)) se denominan iónicos porque describen ocupaciones orbitales atómicas, que son apropiadas a la\(R \rightarrow \infty\) región que corresponde a\(X \bullet\bullet + X \) y estructuras de enlace de\(X + X \bullet\bullet\) valencia, mientras que\(|s_x \alpha s_y \beta|\) y\(|s_y \alpha s_x \beta|\) se llaman “covalentes” porque corresponden a\(X\bullet + X\bullet\) estructuras.
De manera similar, las cinco funciones determinantes restantes pueden expresarse en términos de determinantes de Slater basados en fragmentos orbitales. Al hacerlo, se hace uso de la antisimetría de los determinantes de Slater (e.g.,\(| \phi_1 \phi_2 \phi_3 | = - | \phi_1 \phi_3 \phi_2 |\)), lo que implica que se desvanece cualquier determinante en el que dos o más orbitales espín sean idénticos\(| \phi_1 \phi_2 \phi_2 | = - | \phi_1 \phi_2 \phi_2 | = 0\). El resultado de descomponer los determinantes basados en MO en sus componentes fragmento-orbitales es el siguiente:
\[ {}^1\Sigma^{**} (0) = |\sigma^*\alpha \sigma^*\beta | = C^*{}^2 [ |s_x \alpha s_x \beta| + |s_y \alpha s_y \beta| - |s_x \alpha s_y \beta| - |s_y \alpha s_x \beta|]\]
\[ {}^1\Sigma^{*} (0) =\frac{1}{\sqrt{2}}[ |\sigma\alpha \sigma^*\beta | - |\sigma\beta \sigma^*\alpha | ]= CC^* \sqrt{2} [|s_x \alpha s_x \beta| - |s_y \alpha s_y \beta|] \]
\[ {}^3\Sigma^{*} (1) = |\sigma\alpha \sigma^*\alpha | = CC^* 2|s_y \alpha s_x \alpha|\]
\[ {}^3\Sigma^{*} (0) = \frac{1}{\sqrt{2}}[ \sigma\alpha \sigma^*\beta | + |\sigma\beta \sigma^*\alpha |]=CC^* \sqrt{2} [|s_y \alpha s_x \beta| - |s_x \alpha s_y \beta|]\]
\[ {}^3\Sigma^{*} (-1) = |\sigma\alpha \sigma^*\alpha | = CC^* 2|s_y \beta s_x \beta|\]
Estas descomposiciones de los seis determinantes de valencia en componentes de enlace fragmento-orbital o valencia permiten especificar las\(R = \infty\) energías de estos estados. Por ejemplo, el hecho de que ambas\({}^1\Sigma\) y\({}^1\Sigma^{**}\) contengan 50% de estructuras iónicas y 50% covalentes implica que, como\(R \rightarrow \infty\), ambas energías se acercarán al promedio de las energías atómicas covalentes e iónicas\(\frac{1}{2} [E (X\bullet ) + E (X\bullet ) + E (X) + E ( X \bullet\bullet) ]\). La\({}^1\Sigma^{*}\) energía se acerca al valor puramente iónico\(E (X)+ E (X \bullet\bullet )\) como\(R \rightarrow \infty\). Las energías de\({}^3\Sigma^{*}(0), {}^3\Sigma^{*}(1)\) y\({}^3\Sigma^{*}(-1)\) todos se acercan al valor puramente covalente\(E (X\bullet ) + E (X\bullet )\) como\(R \rightarrow \infty\).
Los comportamientos de las energías de los seis determinantes de valencia como\(R\) varía se representan en la Figura 6.1.13 para situaciones en las que se favorece energéticamente la escisión del enlace homolítico (es decir, para las cuales\(E (X\bullet ) + E (X\bullet ) < E (X) +E ( X \bullet\bullet)\)).
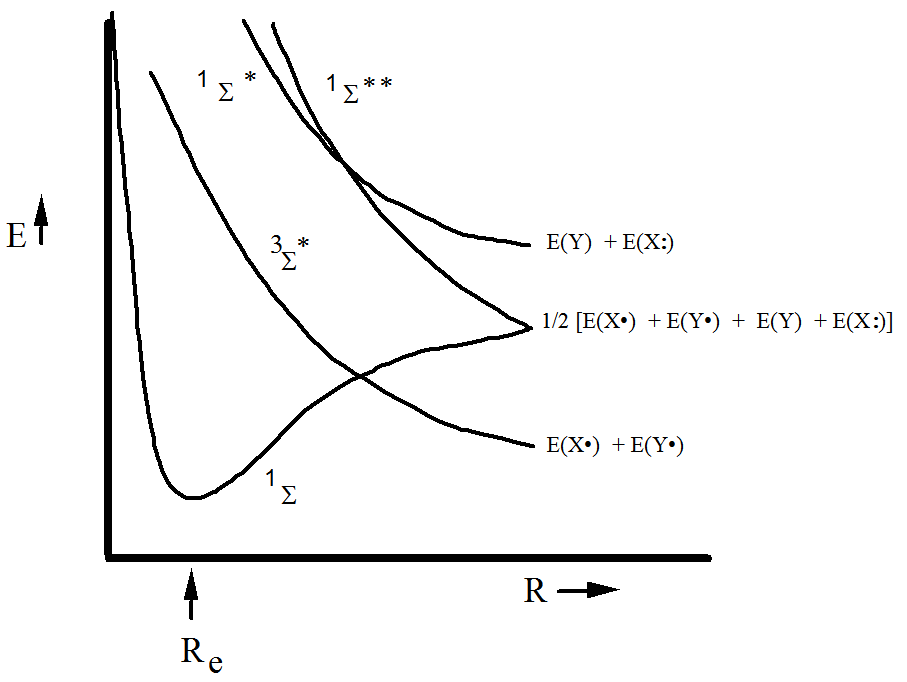
Es esencial darse cuenta de que las energías de los determinantes no representan las energías de los verdaderos estados electrónicos. Para\(R\) -valores en los que las energías determinantes están ampliamente separadas, las energías del estado verdadero son bastante bien aproximadas por energías determinantes individuales; tal es el caso cerca de Re para el\({}^1\Sigma\) estado.
Sin embargo, en general\(R\), la situación es muy diferente, y es en tales casos que ocurre lo que denominamos interacción de configuración esencial. Específicamente, para el\(X=Y\) ejemplo,\({}^1\Sigma^{**}\) los determinantes\({}^1\Sigma\) y se someten a acoplamiento de CI esencial para formar un par de estados de\({}^1\Sigma\) simetría (el\({}^1\Sigma^{*}\) CSF no puede participar en esta mezcla de CI porque es de simetría desgerada; los\({}^3\Sigma^{*}\) estados no pueden mezclarse porque son de simetría de giro triplete). La mezcla de IC de\({}^1\Sigma^{**}\) los determinantes\({}^1\Sigma\) y se describe en términos de un problema secular 2x2
\ [\ left [\ begin {array} {cc}
\ langle ^1\ Sigma | H | ^1\ Sigma\ rangle &\ langle ^1\ Sigma | H | ^1\ Sigma^ {**}\ rangle\\
\ langle ^1\ Sigma^ {**} | H | ^1\ Sigma\ rangle &\ langle ^1\ Sigma^ {**} | H | 1\ Sigma^ {**}\ rangle
\ end {array}\ right]
\ left [\ begin {array} {c} A\\ B\ end {array}\ right]
= E\ left [\ begin {array} {c} A\\ B\ end {array}\ derecha]\]
Las entradas diagonales son las energías de los determinantes representadas en la Figura 6.1.13. Los elementos de la matriz de acoplamiento fuera de la diagonal se pueden expresar en términos de una integral de intercambio entre los\(\sigma^*\) orbitales\(\sigma\) y:
\[\langle {}^1\Sigma|H|{}^1\Sigma^{**} \rangle = \langle |\sigma\alpha \sigma\beta|H||\sigma^*\alpha \sigma^*\beta |\rangle = \langle \sigma\sigma|| \sigma^*\sigma^* \rangle = K_{\sigma \sigma^*}\]
Posteriormente en este Capítulo, aprenderás a evaluar los elementos de la matriz hamiltoniana entre pares de funciones de onda antisimétricas y a expresarlos en términos de integrales de uno y dos electrones. Si estás ansioso por aprender esto ahora, ve a la subsección titulada Reglas de Slater-Condon y lee eso antes de regresar aquí.
En\(R \rightarrow \infty\), donde los\({}^1\Sigma^{**}\) determinantes\({}^1\Sigma\) y son degenerados, las dos soluciones al problema de valores propios de la matriz de CI anterior son:
\[ E =\frac{1}{2} [ E (X\bullet ) + E (X\bullet ) + E (X)+ E (X \bullet\bullet) ] \mp \langle \sigma\sigma | \frac{1}{r_{12}} | \sigma^* \sigma^*\rangle \]
con amplitudes respectivas para los\({}^1\Sigma\) y los\({}^1\Sigma^{**}\) MCA dadas por
\[ A_\mp = \pm \frac{1}{\sqrt{2}} ; \hspace{15pt} B_{\mp} = \mp \frac{1}{\sqrt{2}}.\]
La primera solución tiene así
\[ \psi_{-} = \frac{1}{\sqrt{2}} [|\sigma\alpha \sigma\beta| - |\sigma^*\alpha \sigma^*\beta |]\]
que, cuando se descompone en componentes orbitales atómicos, produce
\[\psi_{-} = \frac{1}{\sqrt{2}} [ |s_x\alpha s_y\beta| - |s_x\beta s_y\alpha|].\]
La otra raíz tiene
\[ \psi_{+} = \frac{1}{\sqrt{2}} [|\sigma\alpha \sigma\beta| + |\sigma^*\alpha \sigma^*\beta |] = \frac{1}{\sqrt{2}} [ |s_x\alpha s_x\beta| + |s_y a s_y\beta|].\]
Entonces, vemos eso\({}^1\Sigma\) y\({}^1\Sigma^{**}\), que ambas contienen 50% de partes iónicas y 50% covalentes, se combinan para producir\(\psi_{-}\) lo que es puramente covalente y\(\psi_{+}\) que es puramente iónico.
La mezcla esencial de CI anterior de\({}^1\Sigma\) y\({}^1\Sigma^{**}\) como altera\(R \rightarrow \infty\) cualitativamente los diagramas de energía mostrados anteriormente. Las descripciones de los estados de valencia singlete y triplete S resultantes se dan en la Figura 6.1.14 para situaciones homonucleares en las que los productos covalentes se encuentran por debajo de los fragmentos iónicos.
Figura 6.1.14: Diagrama de correlación estatal que muestra cómo las energías de los Estados, compuestas por combinaciones de determinantes, varían con\(R\).


