6.9: Sondas Experimentales de Estructura Electrónica
- Page ID
- 71047
Espectroscopia Visible y Ultravioleta
Las espectroscopias visibles y ultravioletas se utilizan para estudiar las transiciones entre estados de una molécula o ion en los que cambia la ocupación orbital de los electrones. Llamamos a estas transiciones electrónicas, y suelen requerir luz en el\(^{-1}\) régimen de 5000 cm\(^{-1}\) a 100,000 cm. Cuando ocurren tales transiciones, los estados inicial y final generalmente difieren en sus energías electrónicas, vibracionales y rotacionales porque cualquier cambio en la ocupación orbital de los electrones inducirá cambios en la superficie de energía Born-Oppenheimer que, a su vez, gobierna el carácter vibracional y rotacional. Las excitaciones de los electrones orbitales internos y centrales pueden requerir fotones de energía aún más alta como lo harían las excitaciones que expulsan un electrón. La interpretación de todos estos datos espectroscópicos se basa en gran medida en la teoría como esta Sección está diseñada para ilustrar.
El dipolo electrónico de transición y el uso de la simetría de grupo puntual
La interacción de la radiación electromagnética con los electrones y núcleos de una molécula se puede tratar utilizando la teoría de la perturbación como se discutió en el Capítulo 4. El resultado es una expresión estándar que derivamos en el Capítulo 4
\[R_{i,f} = \frac{2\pi}{\hbar^2} f(\omega_{f,i}) | \textbf{E}_0· \langle \Phi_f | \boldsymbol{\mu} | \Phi_i\rangle |^2\]
para la tasa de absorción de fotones entre\(\Phi_f\) los estados inicial\(\Phi_i\) y final. En esta ecuación,\(f(\omega)\) se encuentra la intensidad de la fuente de fotones a la frecuencia\(\omega\),\(\omega_{f,i}\) es la frecuencia correspondiente a la transición en estudio, y\(\textbf{E}_0\) es el vector de campo eléctrico del campo de fotones. El vector\(\boldsymbol{\mu}\) es el momento dipolar eléctrico de los electrones y núcleos en la molécula.
Debido a que cada una de estas funciones de onda es producto de un ye electrónico, una vibracional y una función de rotación, nos damos cuenta de que la integral electrónica que aparece en esta expresión de velocidad implica
\[\langle \psi_{ef} | \boldsymbol{\mu} | \psi_{ei}\rangle = \boldsymbol{\mu}_{f,i} (R),\]
un elemento de matriz de dipolo de transición entre las funciones de onda\(\psi_{ef}\) electrónica inicial\(\psi_{ei}\) y final. Este elemento es una función de las coordenadas vibracionales internas de la molécula, y es un vector bloqueado al marco del eje interno de la molécula.
La simetría molecular de grupos de puntos a menudo se puede usar para determinar si un elemento de matriz dipolar de una transición particular desaparecerá y, como resultado, se prohibirá la transición electrónica y, por lo tanto, se predecirá que tendrá intensidad cero. Si el producto directo de las simetrías de los estados electrónicos inicial y final\(\psi_{ei}\) y\(\psi_{ef}\) no coinciden con la simetría del operador dipolo eléctrico (que tiene la simetría de sus\(x\),\(y\), y\(z\) componentes; estas simetrías se pueden leer en la columna más derecha de las tablas de caracteres), el elemento matriz se desvanecerá.
Por ejemplo, la molécula de formaldehído\(H_2CO\) tiene un estado electrónico básico que tiene\(^1A_1\) simetría en el grupo de\(C_{2v}\) puntos. Su estado excitado\(\pi \Rightarrow \pi^*\) singlete también tiene\(^1A_1\) simetría porque tanto los\(\pi\) orbitales como\(\pi^*\) los orbitales son de\(b_1\) simetría. En contraste, el estado excitado singlete más bajo\(n \Rightarrow \pi^*\) (estos orbitales se muestran en la Figura 6.15) es de\(^1A_2\) simetría debido a que el orbital no enlazante centrado en oxígeno de mayor energía es de\(b_2\) simetría y el\(\pi^*\) orbital es de\(b_1\) simetría, por lo que el determinante Slater en el que tanto los\(n\)\(\pi^*\) orbitales como los orbitales están ocupados individualmente tiene su simetría dictada por el producto\(b_2 \times b_1\) directo, que es\(A_2\).
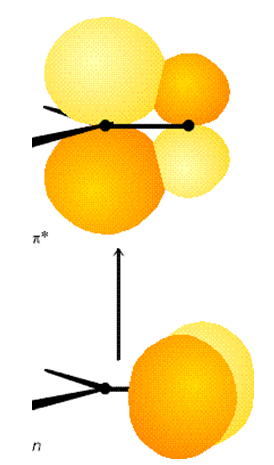
La\(\pi \Rightarrow \pi^*\) transición implica así estados tierra (\(^1A_1\)) y excitado (\(^1A_1\)) cuyo producto directo (\(A_1 \times A_1\)) es de\(A_1\) simetría. Por lo tanto, esta transición requiere que el operador de dipolo eléctrico posea un componente de\(A_1\) simetría. Un vistazo a la tabla de caracteres del grupo\(C_{2v}\) puntual muestra que el\(z\) eje molecular es de\(A_1\) simetría. Por lo tanto, si el campo eléctrico de la luz tiene un componente distinto de cero a lo largo del eje de\(C_2\) simetría (el\(z\) eje de la molécula), se predice que se permita la\(\pi \Rightarrow \pi^*\) transición. La luz polarizada a lo largo de cualquiera de los otros dos ejes de la molécula no puede inducir esta transición.
En contraste, la\(n \Rightarrow \pi^*\) transición tiene un estado excitado por el suelo producto directo de la\(B_2\times B_1=A_2\) simetría. La tabla de caracteres\(C_{2v}\) del grupo de puntos muestra que el operador dipolo eléctrico (es decir\(x\), su\(y\), y\(z\) componentes en el marco fijo molecular) no tiene componente de\(A_2\) simetría; por lo tanto, la luz sin orientación de campo eléctrico puede inducir esta\(n \Rightarrow \pi^*\) transición. Decimos así que la\(n \Rightarrow \pi^*\) transición está prohibida.
Los ejemplos anteriores ilustran una de las aplicaciones más importantes de la espectroscopía UV visible. La información obtenida en tales experimentos puede ser utilizada para inferir las simetrías de los estados electrónicos y, por ende, de los orbitales ocupados en estos estados. Es de esta manera que este tipo de experimentos sondea estructuras electrónicas.
Los factores Franck-Condon
Más allá de dicho análisis electrónico de simetría, también es posible derivar reglas de selección vibracional para las transiciones electrónicas que se permiten. Es convencional expandir el elemento de matriz de dipolo de transición\(\boldsymbol{\mu}_{f,i} (R)\) en una serie de potencias alrededor de la geometría de equilibrio del estado electrónico inicial (ya que esta geometría es característica de la estructura molecular anterior a la absorción de fotones y, debido a que la absorción de fotones se produce rápidamente, los núcleos no tienen tiempo para moverse lejos de ahí):
\[\boldsymbol{\mu}_{f,i}(R) = \boldsymbol{\mu}_{f,i}(R_e) + \sum_a \frac{\partial \boldsymbol{\mu}_{f,i}}{∂R_a} (R_a - R_{a,e}) + ....\]
El primer término en esta expansión, cuando se sustituye en la integral sobre las coordenadas vibracionales, da\(\boldsymbol{\mu}_{f,i}(R_e) \langle \chi_{v_f} | \chi_{v_i}\rangle \), que tiene la forma del dipolo de transición electrónico multiplicado por la integral de superposición entre las funciones de onda vibratoria inicial y final. El\(\boldsymbol{\mu}_{f,i}(R_e)\) factor se discutió anteriormente; es la integral de transición electrónica evaluada en la geometría de equilibrio del estado absorbente. A menudo se puede utilizar la simetría para determinar si esta integral desaparece, como resultado de lo cual se prohibirá la transición.
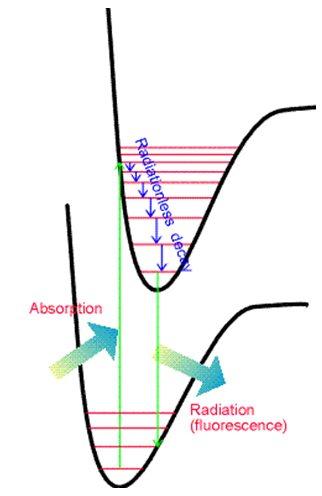
Las integrales de superposición vibracional\(\langle \chi_{v_f} | \chi_{v_i}\rangle \) no necesariamente desaparecen porque\(\chi_{v_f}\) y\(\chi_{v_i}\) son funciones propias de diferentes hamiltonianos vibracionales porque pertenecen a diferentes superficies energéticas Born-Oppenheimer. \(\chi_{v_f}\)es una función propia cuya energía potencial es la superficie de energía del estado electrónico final;\(\chi_{v_i}\) tiene como potencial la superficie de energía del estado electrónico inicial. Los cuadrados de estas\(\langle \chi_{v_f} | \chi_{v_i}\rangle \) integrales, que son los que eventualmente entran en la expresión de la tasa de transición\(R_{i,f} = \frac{2\pi}{\hbar^2} f(\omega_{f,i}) | \textbf{E}_0· \langle \Phi_f | \boldsymbol{\mu} | \Phi_i\rangle |^2\), se denominan factores Franck-Condon. Sus magnitudes relativas juegan un papel importante en la determinación de las intensidades relativas de varias bandas vibracionales (es decir, series de picos) dentro del espectro de una transición electrónica particular. En la Figura 6.16, muestro dos curvas de energía potencial e ilustramos los tipos de transiciones de absorción (y emisión) que pueden ocurrir cuando los dos estados electrónicos tienen geometrías significativamente diferentes.
Siempre que una transición electrónica provoca un gran cambio en la geometría (longitudes de enlace o ángulos) de la molécula, los factores Franck-Condon tienden a mostrar la progresión amplia característica mostrada en la Figura 6.17 cuando se consideran para un nivel vibracional de estado inicial\(v_i\) y varios estados finales niveles vibracionales\(v_f\):
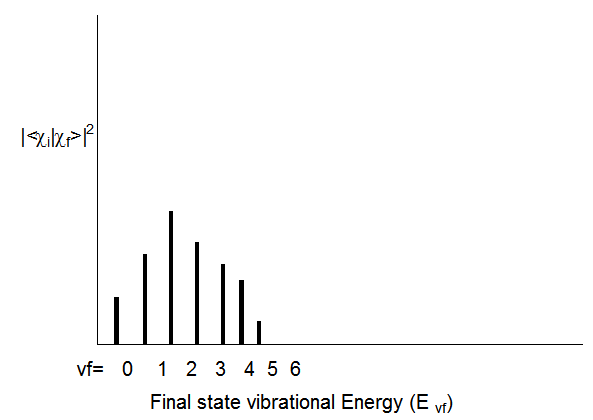
Observe que a medida que uno se mueve a\(v_f\) valores más altos, disminuye el espaciamiento de energía entre los estados (Evf - Evf-1); esto, por supuesto, refleja la anarmonicidad en el potencial vibratorio del estado excitado. Para el ejemplo anterior, la transición al\(v_f = 2\) estado tiene el mayor factor Franck-Condon. Esto significa que la superposición de la función de onda vibratoria del estado inicial\(\chi_{v_i}\) es mayor para la\(\chi_{v_f}\) función del estado final con\(v_f = 2\).
Como regla empírica cualitativa, cuanto mayor sea la diferencia geométrica entre los potenciales de estado inicial y final, más amplio será el perfil de Franck-Condon (como se muestra en la Figura 6.17) y mayor será el\(v_f\) valor para el cual este perfil alcanza su punto máximo. Las diferencias en las frecuencias armónicas entre los dos estados también pueden ampliar el perfil Franck-Condon.
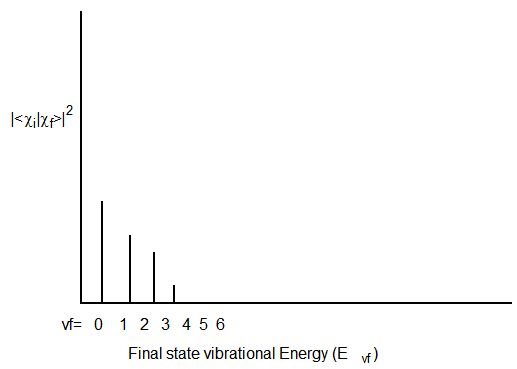
Si los estados inicial y final tienen geometrías y frecuencias muy similares a lo largo del modo que se excita cuando se realiza la excitación electrónica particular, el tipo de perfil Franck-Condon que se muestra en la Figura 6.18 puede resultar:
Otra característica que es importante destacar es la relación entre absorción y emisión cuando las superficies energéticas de los dos estados tienen diferentes geometrías o frecuencias de equilibrio. Posterior a la absorción de fotones para formar un estado electrónico excitado pero previo a la emisión de fotones, la molécula puede sufrir colisiones con otras moléculas cercanas. Esto, por supuesto, es especialmente cierto en los experimentos en fase condensada. Estas colisiones hacen que la molécula excitada pierda parte de su energía vibratoria y rotacional, relajándola a niveles más bajos en la superficie electrónica excitada. Este proceso de relajación se ilustra en la Figura 6.19.
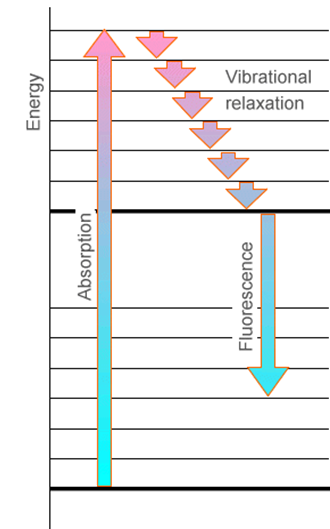
Posteriormente, la molécula excitada electrónicamente puede sufrir emisión de fotones (también llamada fluorescencia) para regresar a su estado electrónico básico como se muestra en la Figura 6.20.
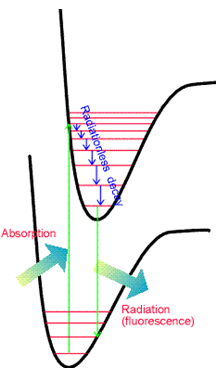
El principio Franck-Condon discutido anteriormente también rige las intensidades relativas de las diversas transiciones vibracionales que surgen en dichos procesos de emisión. Así, nuevamente se observa un conjunto de picos en el espectro de emisión como se muestra en la Figura 6.21.

Hay dos diferencias entre las líneas que ocurren en emisión y en absorción. Primero, las líneas de emisión se desplazan al rojo (es decir, para reducir la energía o longitud de onda más larga) porque ocurren en energías de transición que conectan el nivel vibratorio más bajo del estado electrónico superior a varios niveles del estado inferior. En contraste, las líneas de absorción conectan el nivel vibratorio más bajo del estado fundamental a varios niveles del estado superior. Estas relaciones se muestran en la Figura 6.22.
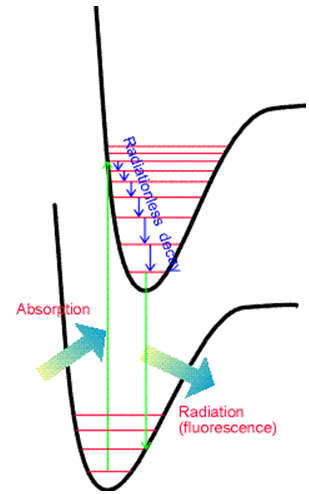
La segunda diferencia se relaciona con los espaciamientos entre las líneas vibracionales. En emisión, estos espaciamientos reflejan los espaciamientos de energía entre los niveles vibracionales del estado fundamental, mientras que en la absorción reflejan espaciamientos entre los niveles vibracionales del estado superior.
Los ejemplos anteriores ilustran cómo se pueden usar los espectros de absorción y emisión de UV visible resueltos por vibración para obtener información valiosa sobre
- las separaciones del nivel de energía vibratoria de los estados electrónicos superior y terrestre (estos espaciamientos, a su vez, reflejan las fortalezas de los enlaces existentes en estos estados),
- el cambio en la geometría que acompaña a la transición electrónica del estado de tierra a excitado como se refleja en la amplitud de los perfiles Franck-Condon (estos cambios también nos hablan de los cambios de unión que ocurren a medida que ocurre la transición electrónica).
Entonces, nuevamente vemos cómo se puede utilizar la espectroscopia visible-UV para aprender sobre la estructura electrónica de las moléculas en diversos estados electrónicos.
Expresiones de función de correlación de tiempo para tasas de
La expresión denominada regla de oro anterior para las tasas de transiciones inducidas por fotones se escribe en términos de los estados electrónico/vibracional/rotacional inicial y final de la molécula. Hay situaciones en las que estos estados simplemente no se pueden conocer de manera confiable. Por ejemplo, los estados vibracionales superiores de una molécula poliatómica grande o los estados de una molécula que interactúa fuertemente con las moléculas solventes circundantes son tales casos. En tales circunstancias, es posible reformular la fórmula de la regla de oro en una forma que sea más susceptible de introducir modelos físicos específicos que conduzcan a conocimientos adicionales.
Específicamente, mediante el uso de las llamadas funciones de correlación de tiempo promediado en equilibrio, es posible obtener expresiones de velocidad apropiadas para un gran número de moléculas que existen en una distribución de estados iniciales (por ejemplo, para moléculas que ocupan muchos posibles niveles rotacionales y quizás varios niveles vibracionales a temperatura ambiente). Como veremos pronto, tomar esta ruta para expresar las tasas de transición espectroscópicas también nos permite evitar tener que conocer cada función de onda vibracional-rotacional de los dos estados electrónicos involucrados; como se señaló anteriormente, esto es especialmente útil para moléculas grandes o moléculas en medios condensados donde tales es probable que el conocimiento no esté disponible.
Para comenzar a reexpresar las tasas de transición espectroscópica, la expresión obtenida anteriormente
\[R_{i,f} = \frac{2\pi}{\hbar^2} f(\omega_{f,i}) | \textbf{E}_0· \langle \Phi_f | \boldsymbol{\mu} | \Phi_i\rangle |^2 ,\]
apropiado para las transiciones entre un estado inicial particular\(\Phi_i\) y un estado final específico\(\Phi_f\), se reescribe como
\[R_{i,f} = \frac{2\pi}{\hbar^2} \int f(\omega)|\textbf{E}_0 \cdot \langle \Phi_f | \boldsymbol{\mu} | \Phi_i \rangle |^2 \delta(\omega_{f,i}-\omega)d\omega .\]
Aquí, la\(\delta(\omega_{f,i} - \omega)\) función se utiliza para imponer específicamente la condición de resonancia que establece que la frecuencia de los fotones\(\omega\) debe ser resonante con la frecuencia de transición\(\omega_{f,i}\). La siguiente identidad integral se puede utilizar para reemplazar la\(d\) función -function:
\[\delta(\omega_{f,i} - \omega) = \frac{1}{\pi} \int_{-\infty}^\infty \exp[i(\omega_{f,i}-\omega)t] dt \]
por una forma que es más susceptible de un mayor desarrollo. Entonces, la tasa de transición de estado a estado se convierte en:
\[R_{i,f} = \frac{1}{\hbar^2} \int f(\omega) |\textbf{E}_0 \cdot \langle \Phi_f | \boldsymbol{\mu} | \Phi_i \rangle |^2 \int_{-\infty}^\infty \exp[i(\omega_{f,i}-\omega)t] dt d\omega .\]
Si esta expresión se multiplica entonces por la probabilidad de equilibrio de\(\rho_i\) que la molécula se encuentre en el estado\(\Phi_i\) y se sume sobre todos esos estados iniciales y se sume sobre todos los estados finales\(\Phi_f\) que se puedan alcanzar desde\(\Phi_i\) con fotones de energía\(\hbar\omega\), el equilibrio Se obtiene la tasa promedio de absorción de fotones por la muestra molecular:
\[R_{\rm eq.ave.} = \frac{1}{\hbar^2}\sum_{f,i} \rho_i \int f(\omega) |\textbf{E}_0 \cdot \langle \Phi_f | \boldsymbol{\mu} | \Phi_i \rangle |^2 \int_{-\infty}^\infty \exp[i(\omega_{f,i}-\omega)t] dt d\omega.\]
Esta expresión es apropiada para un conjunto de moléculas que pueden estar en diversos estados iniciales\(\Phi_i\) con probabilidades\(\rho_i\). El resultado correspondiente para las transiciones que se originan en un estado particular (\(\Phi_i\)) pero terminan en cualquiera de los estados finales permitidos (por reglas de energía y selección) dice:
\[R_i = \frac{1}{\hbar^2}\sum_{f} \rho_i \int f(\omega) |\textbf{E}_0 \cdot \langle \Phi_f | \boldsymbol{\mu} | \Phi_i \rangle |^2 \int_{-\infty}^\infty \exp[i(\omega_{f,i}-\omega)t] dt d\omega.\]
Como discutimos en el Capítulo 7, para un conjunto en el que se especifican el número de moléculas\(T\), la temperatura y el volumen del sistema,\(\rho_i\) toma la forma:
\[\rho_i = g_i \exp(-E_i^0/kT)/Q\]
donde\(Q\) está la función de partición de las moléculas y\(g_i\) es la degeneración del estado\(\Phi_i\) cuya energía es\(E_i^0\). Si no está familiarizado con las funciones de partición y no quiere simplemente confiar en mí en el análisis de las funciones de correlación de tiempo que estamos a punto de emprender, le sugiero que interrumpa su estudio del Capítulo 6 y lea en este momento la Sección 7.1.3 del Capítulo 7.
En la expresión anterior for\(R_{\rm eq.ave.}\), se produce una doble suma. Escribiendo en detalle los elementos que aparecen en esta suma, se encuentra:
\[\sum_{i,f} \rho_i \textbf{E}_0· \langle \Phi_i | \boldsymbol{\mu} | \Phi_f\rangle \textbf{E}_0· \langle \Phi_f | \boldsymbol{\mu} | \Phi_i\rangle \exp[i(\omega_{f,i})t].\]
En situaciones en las que uno está interesado en desarrollar una expresión para la intensidad que surge de las transiciones a todos los estados finales permitidos, la suma sobre los estados finales puede llevarse a cabo explícitamente por escrito primero
\[\langle \Phi_f | \boldsymbol{\mu} | \Phi_i\rangle \exp[i(\omega_{f,i})t] = \langle \Phi_f |\exp(iHt/\hbar) \boldsymbol{\mu} \exp(-iHt/\hbar)| \Phi_i\rangle \]
y luego usando el hecho de que el conjunto de estados {\(\Phi_k\)} son completos y por lo tanto obedecen
\[\sum_k |\Phi_k\rangle \langle \Phi_k| = 1.\]
El resultado de usar estas identidades así como la definición de Heisenberg de la dependencia del tiempo del operador dipolo
\[\boldsymbol{\mu}(t) = \exp(iHt/\hbar) \boldsymbol{\mu} \exp(-iHt/\hbar),\]
es:
\[\sum_i\rho_i \langle \Phi_i | \textbf{E}_0· \boldsymbol{\mu} \textbf{E}_0· \boldsymbol{\mu} (t) | \Phi_i\rangle .\]
De esta forma, se dice que la dependencia del tiempo se ha reducido a la de una función de correlación de tiempo promediada en equilibrio (es decir, como se refleja en la\(\sum_i \rho_i \langle \Phi_i | | \Phi_i\rangle \) expresión) que involucra el componente del operador dipolo a lo largo del campo eléctrico externo en\(t = 0\),\(( \textbf{E}_0· \boldsymbol{\mu} )\) y este componente en una tiempo diferente\(t\),\((\textbf{E}_0· \boldsymbol{\mu} (t))\).
Si\(\omega_{f,i}\) es positivo (es decir, en el caso de absorción de fotones), la expresión anterior producirá una contribución distinta de cero cuando se multiplique por\(\exp(-i\omega t)\) e integrada sobre valores positivos\(\omega\). Si\(\omega_{f,i}\) es negativo (en cuanto a la emisión estimulada de fotones), esta expresión contribuirá, cuando se multiplique por\(\exp(-i\omega t)\), para\(\omega\) valores negativos. En esta última situación,\(\rho_i\) se encuentra la probabilidad de equilibrio de encontrar la molécula en el estado (excitado) a partir del cual se producirá la emisión; esta probabilidad puede estar relacionada con la del estado inferior\(\rho_f\) por
\[\begin{align*} \rho_{\rm excited} &= \rho_{\rm lower} \exp[ - (E^0_{\rm excited} - E^0_{\rm lower})/kT ] \\[4pt] &= \rho_{\rm lower} \exp[ - \hbar\omega/kT ]. \end{align*}\]
Los casos de absorción y emisión se pueden combinar en una sola expresión para la tasa neta de absorción de fotones reconociendo que este último proceso conduce a la producción de fotones, y así debe ingresarse con un signo negativo. La expresión resultante para la tasa neta de disminución de fotones es:
\[R_{\rm eq.ave.net} = \frac{1}{\hbar^2} \sum_i \rho_i\]
\[\int \int f(\omega) \langle \Phi_i | (\textbf{E}_0· \boldsymbol{\mu}) \textbf{E}_0· \boldsymbol{\mu} (t) | \Phi_i\rangle (1 - \exp(- \hbar\omega/kT) ) \exp(-i\omega t) d\omega dt.\]
Es convención introducir la llamada función de forma de línea\(I (\omega)\):
\[I (\omega) = \sum_i \rho_i \exp(-i\omega t) dt\]
en términos de los cuales la tasa neta de absorción de fotones es
\[R_{\rm eq.ave.net} = \frac{1}{\hbar^2} (1 - \exp(- \hbar\omega/kT) ) .\]
La función
\[C (t) = \sum_i \rho_i \langle \Phi_i | (\textbf{E}_0· \boldsymbol{\mu} ) \textbf{E}_0· \boldsymbol{\mu} (t) | \Phi_i\rangle \]
se denomina función de correlación de tiempo promedio de equilibrio del componente del operador dipolo eléctrico a lo largo de la dirección del campo eléctrico externo\(E_0\). Su transformada de Fourier es\(I (\omega)\), la función de forma de línea espectral. La convolución de\(I(\omega)\) con la\(f (\omega)\) función de la fuente de luz, multiplicada por\((1 - \exp(-\hbar\omega/kT)\)), la corrección para la emisión estimulada de fotones, da la tasa neta de absorción de fotones.
Aunque la expresión de la función de correlación para la tasa de absorción de fotones es equivalente a la expresión de estado a estado de la que se derivó, notamos que
- \(C(t)\)no contiene referencia explícita a las funciones de onda de estado final\(\phi\); en su lugar,
- \(C(t)\)nos obliga a describir cómo el operador del dipolo cambia con el tiempo.
Es decir, en el marco de correlación temporal, se permite utilizar modelos de la evolución temporal del sistema para describir los espectros. Esto es especialmente atractivo para moléculas complejas grandes y moléculas en medios condensados porque, para tales sistemas, sería desesperado intentar encontrar las funciones de onda de estado final, pero puede ser razonable (aunque desafiante) modelar la evolución temporal del sistema. El profesor Eric Heller de Harvard ha sido pionero en el uso de métodos de dominio temporal para el tratamiento de la espectroscopia molecular; su sitio web ofrece acceso a más información y conocimiento sobre este tema.
Resulta que una gran variedad de propiedades espectroscópicas y termodinámicas (por ejemplo, intensidades de dispersión de luz, coeficientes de difusión y conductividad térmica) se pueden expresar en términos de funciones de correlación molecular de tiempo. El texto Mecánica Estadística, D. A. McQuarrie, Harper y Row, Nueva York (1977) tiene un buen tratamiento de muchos de estos casos. Examinemos ahora cómo se utilizan esos problemas de evolución temporal dentro del marco de la función de correlación para el caso específico de absorción de fotones.
Mecanismos de ampliación de líneas
Si se supone que el movimiento de rotación de las moléculas del sistema está completamente libre de obstáculos (por ejemplo, por cualquier entorno o por colisiones con otras moléculas), es apropiado expresar la dependencia del tiempo de cada una de las funciones de correlación de tiempo dipolo enumeradas anteriormente en términos de un modelo de rotación libre. Por ejemplo, cuando se trata de moléculas diatómicas, la electrónica-vibracional-rotacional\(C(t)\) apropiada para una transición electrónica-vibracional específica se convierte en:
\[C(t) = (q_r q_v q_e q_t)^{-1} \sum_J (2J+1) \exp\bigg(- \frac{\hbar^2J(J+1)}{8\pi^2IkT}\bigg) \exp\Big(- \frac{\hbar\nu_{\rm vib}v_i}{kT}\Big)\]
\[g_{ie} \langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle |\langle \chi_{iv} | \chi_{fv}\rangle |^2\]
\[\exp(i [\hbar\nu_{\rm vib}] t + i\Delta E_{i,f} t/\hbar).\]
Aquí,
\[q_r = \frac{8\pi^2IkT}{\hbar^2}\]
es la función de partición rotacional (siendo I el momento de inercia de la molécula\(I = mR_e^2\), y\(\dfrac{\hbar^2J(J+1)}{8\pi^2I}\) siendo la energía rotacional de la molécula para el estado con número cuántico\(J\) y degeneración\(2J+1\)),
\[q_v = \frac{\exp(-\hbar\nu_{\rm vib}/2kT)}{1-\exp(-\hbar\nu_{\rm vib}/kT)}\]
es la función de partición vibracional\(\nu_{\rm vib}\) siendo la frecuencia vibracional),\(g_{ie}\) es la degeneración del estado electrónico inicial,
\[q_t = (2\pi mkT/\hbar^2)^{3/2} V\]
es la función de partición traslacional para las moléculas de masa que\(\boldsymbol{\mu}\) se mueven en volumen\(V\), y\(\Delta E_{i,f}\) es el espaciamiento de la energía electrónica adiabática. Los orígenes de tales funciones de partición se tratan en el Capítulo 7 de este texto.
Las funciones\(\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle \) describen la evolución temporal del vector dipolo de transición electrónica para el estado rotacional\(J\). En un modelo de rotación libre, esta función se toma como de la forma:
\[\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle \]
\[= \langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) |\phi_J\rangle \cos(\omega_Jt)\]
donde\(\omega_J\) es la frecuencia de rotación (en ciclos por segundo) para la rotación de la molécula en el estado marcado por\(J\). Esta dependencia oscilatoria del tiempo, combinada con la dependencia\(\exp(i [\hbar\nu_{\rm vib}] t + i\Delta E_{i,f} t/\hbar)\) temporal derivada de los factores electrónicos y vibracionales, producen, cuando esta\(C(t)\) función es transformada de Fourier para generar\(I(\omega)\), una serie\(d\) de picos de función. Las intensidades de estos picos se rigen por las cantidades
\[(q_r q_v q_e q_t)^{-1} \sum_J (2J+1) \exp\bigg(- \frac{\hbar^2J(J+1)}{8\pi^2IkT}\bigg) \exp\Big(- \frac{\hbar\nu_{\rm vib}v_i}{kT}\Big) g_{ie},\]
Factores poblacionales de Boltzmann, así como por los factores\(|\langle \chi_{iv} | \chi_{fv}\rangle |^2\) Franck-Condon y los\(\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,0) |\phi_J\rangle \) términos.
Este mismo análisis se puede aplicar a las dependencias puras de rotación y vibración-rotación\(C(t)\) con resultados análogos. En el primero, se prevé que los picos de\(d\) función -ocurran en
\[\omega = ± \omega_J\]
y en este último en
\[\omega = \omega_{fv,iv} ± \omega_J ;\]
con las intensidades regidas por los factores independientes del tiempo en las expresiones correspondientes para\(C(t)\).
En las mediciones experimentales, tales\(d\) picos agudos de función, por supuesto, no se observan. Incluso cuando se utilizan fuentes de luz láser de ancho de banda muy estrecho (es decir, para lo cual\(f(\omega)\) es una función de pico extremadamente estrecho), se encuentra que las líneas espectrales poseen anchuras finitas. Discutamos ahora varias fuentes de ampliación de líneas, algunas de las cuales se relacionarán con desviaciones del modelo de movimiento rotacional “sin obstáculos” introducido anteriormente.
Ampliamiento Doppler
En las expresiones anteriores para\(C(t)\), se muestra explícitamente el promedio sobre los estados rotacionales, vibracionales y electrónicos iniciales. También hay un promedio sobre el movimiento traslacional implícito en todas estas expresiones. Su papel no se ha enfatizado (todavía) porque los niveles de energía molecular, cuyos espaciamientos producen las frecuencias características a las que la luz puede ser absorbida o emitida, no dependen del movimiento traslacional. Sin embargo, la frecuencia del campo electromagnético que experimentan las moléculas en movimiento sí depende de las velocidades de las moléculas, por lo que ahora se debe abordar este tema.
Las clases elementales de física expresan el llamado desplazamiento Doppler de la frecuencia de una onda inducido por el movimiento relativo de la fuente de luz y la molécula de la siguiente manera:
\[\omega_{\rm observed} = \omega_{\rm nominal} (1 + v_z/c)^{-1} \approx \omega_{\rm nominal} (1 - v_z/c + ...).\]
Aquí,\(\omega_{\rm nominal}\) es la frecuencia de la fuente de luz inmóvil vista por las moléculas inmóviles,\(v_z\) es la velocidad del movimiento relativo de la fuente de luz y las moléculas,\(c\) es la velocidad de la luz, y wobservada es la frecuencia desplazada por Doppler (es decir, la frecuencia vista por las moléculas). La segunda identidad se obtiene expandiendo, en una serie de potencias, el\((1 + v_z/c)^{-1}\) factor, y es válido en forma truncada cuando las moléculas se mueven con velocidades significativamente por debajo de la velocidad de la luz.
Para todos los casos considerados anteriormente, una\(C(t)\) función se somete a transformación de Fourier para obtener una función de forma de línea espectral\(I(\omega)\), que luego proporciona el ingrediente esencial para calcular la tasa neta de absorción de fotones. En este proceso de transformada de Fourier,\(\omega\) se supone que la variable es la frecuencia del campo electromagnético experimentado por las moléculas. Las consideraciones anteriores del desplazamiento Doppler llevan entonces a uno a darse cuenta de que la forma funcional correcta a utilizar en la conversión\(C(t)\) a\(I(\omega)\) es:
\[I(\omega) = \int C(t) \exp\left(-i t \omega\Big(1-\dfrac{v_z}{c}\Big)\right)dt,\]
donde\(\omega\) es la frecuencia nominal de la fuente de luz.
Como se dijo anteriormente, dentro también\(C(t)\) hay un promedio de equilibrio sobre el movimiento traslacional de las moléculas. Para una muestra en fase gaseosa sometida a colisiones aleatorias y en equilibrio térmico, este promedio se caracteriza por la conocida distribución de velocidad Maxwell-Boltzmann:
\[\left(\frac{m}{2\pi kT}\right)^{3/2} \exp\bigg(-\frac{m (v_x^2+v_y^2+v_z^2)}{2kT}\bigg) dv_x dv_y dv_z.\]
Aquí\(\boldsymbol{\mu}\) está la masa de las moléculas y\(v_x\),\(v_y\), y\(v_z\) etiquetar las velocidades a lo largo de las coordenadas cartesianas fijadas en laboratorio.
Definir el\(z\) eje -como la dirección de propagación de los fotones de la luz y llevar a cabo el promedio del factor Doppler sobre dicha distribución de velocidad, se obtiene:
\ [\ int_ {-\ infty} ^\ infty\ exp\ izquierda (-i t\ omega\ Grande (1-\ dfrac {v_z} {c}\ Grande)\ derecha)\ izquierda (\ frac {m} {2\ pi kT}\ derecha) ^ {3/2}\ exp\ bigg (-\ frac {m (v_x^2+v_y^2+v2+v^v2+ _z^2)} {2kT}\ bigg) dv_x dv_y dv_z\\
=\ exp (-i\ omega t)\ int_ {-\ infty} ^\ infty\ izquierda (\ frac {m} {2\ pi kT}\ derecha) ^ {1/2}\ exp\ izquierda (it\ omega\ dfrac {v_z} {c}\ derecha)\ exp\ Grande (-\ dfrac {mv_z^2} {2kT}\ Grande) dv_z\]
\[= \exp(-i\omega t) \exp\bigg(- \frac{\omega^2t^2kT}{2mc^2}\bigg).\]
Este resultado, cuando se sustituye en las expresiones for\(C(t)\), produce expresiones idénticas a las dadas para los tres casos tratados anteriormente pero con una sola modificación. El promedio de movimiento traslacional ya no necesita ser considerado en cada uno\(C(t)\); en cambio, las expresiones anteriores para cada una\(C(t)\) deben multiplicarse por un factor\(\exp(- \omega^2t^2kT/(2mc^2))\) que encarna el desplazamiento Doppler promediado traduccional. La función de forma de línea espectral se\(I(\omega)\) puede obtener para cada uno\(C(t)\) simplemente transformando Fourier:
\[I(\omega) = \int_{-\infty}^\infty \exp(-i\omega t)C(t) dt.\]
Cuando se aplica a los casos de rotación, vibración-rotación o vibración-rotación electrónica dentro del modelo de rotación sin obstáculos tratado anteriormente, la transformada de Fourier involucra integrales de la forma:
Esta integral surgiría en el caso electrónico-vibración-rotación; los otros dos casos implicarían integrales de la misma forma pero con la\(\Delta E_{i,f}/\hbar\) ausencia en la situación de vibración-rotación y con\(\omega_{fv,iv} + \Delta E_{i,f}/\hbar\) faltantes para transiciones de rotación pura. Todas estas integrales se pueden llevar a cabo analíticamente y producir:
\[\sqrt{\frac{2mc^2\pi}{\omega^2kT}} \exp\left[ - \frac{(\omega-\omega_{fv,iv} - \Delta E_{i,f}/\hbar ± \omega_J)^2 mc^2}{2\omega^2kT} \right].\]
El resultado es una serie de picos gaussianos en\(\omega\) -espacio, centrados en:
\[\omega = \omega_{fv,iv} + \Delta E_{i,f}/\hbar ± \omega_J\]
con anchuras (\(\sigma\)) determinadas por
\[\sigma^2= \frac{\omega^2kT}{mc^2},\]
dada la temperatura\(T\) y la masa de las moléculas\(m\). Cuanto más caliente es la muestra, más rápido se mueven las moléculas en promedio, y más amplia es la distribución de las frecuencias Doppler desplazadas experimentadas por estas moléculas. El resultado neto del efecto Doppler es producir una función de forma de línea que es similar a la serie de\(d\) funciones del modelo de rotación sin obstáculos pero con cada pico\(d\) de función ensanchado en una forma gaussiana.
Si se pueden obtener espectros con una precisión suficiente para determinar el ancho Doppler de las líneas espectrales, dicho conocimiento se puede utilizar para estimar la temperatura del sistema. Esto puede ser útil cuando se trata de sistemas que no pueden ser sometidos a mediciones de temperatura alternativas. Por ejemplo, se pueden estimar las temperaturas de las estrellas (si se conoce su velocidad relativa a la tierra) determinando los desplazamientos Doppler de las líneas de emisión a partir de ellas. Alternativamente, se puede determinar la velocidad relativa de una estrella de la tierra si se conoce su temperatura. Como otro ejemplo, la temperatura de los gases calientes producidos en una explosión se puede sondear midiendo anchuras Doppler de absorción o líneas de emisión que surgen de moléculas en estos gases.
Amplamiento de Presión
Para incluir los efectos de las colisiones en la parte del movimiento rotacional de cualquiera de las\(C(t)\) funciones anteriores, se debe introducir un modelo de cómo tales colisiones cambian los vectores relacionados con dipolos que entran en\(C(t)\). El modelo más elemental utilizado para abordar colisiones se aplica a muestras gaseosas que se supone que experimentan un movimiento rotacional sin obstáculos hasta ser golpeadas por otra molécula, momento en el que se aplica una patada al vector dipolo y después de lo cual la molécula vuelve a su movimiento rotacional sin obstáculos.
Los efectos de tales patadas inducidas por colisión poco frecuentes se tratan dentro del modelo denominado ensanchamiento de presión (a veces llamado ensanchamiento colisional) modificando la función de correlación de rotación libre mediante la introducción de un factor de amortiguación exponencial\(\exp( -|t|/t)\):
\[\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,0) |\phi_J\rangle \cos \frac{\hbar J(J+1) t}{4\pi I}\]
\[Þ \langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,0) |\phi_J\rangle \cos \frac{\hbar J(J+1) t}{4\pi I} \exp\bigg(-\dfrac{|t|}{\tau}\bigg).\]
Se supone que el parámetro\(\tau\) de escala de tiempo de esta función de amortiguación caracteriza el tiempo promedio entre colisiones y, por lo tanto, debe ser inversamente proporcional a la frecuencia de colisión. Su magnitud también está relacionada con la efectividad con la que las colisiones hacen que la función dipolo se desvíe de su movimiento rotacional sin obstáculos (es decir, relacionado con la fuerza de colisión). En efecto, la amortiguación exponencial hace que la función\(\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle \) de correlación de tiempo pierda su memoria y se desintegre a cero. Este punto de vista de la memoria se basa en la visualización\(\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle \) como la proyección de\(\textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t)\) a lo largo de su\(t = 0\) valor\(\textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,0)\) en función del tiempo t.
Introduciendo esta dependencia adicional del\(\exp( -|t|/t)\) tiempo en\(C(t)\) produce, cuando\(C(t)\) se transforma Fourier para generar\(I(\omega)\), integrales de la forma
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp\bigg(-\dfrac{|t|}{\tau}\bigg) \exp\bigg(- \frac{\omega^2t^2kT}{2mc^2}\bigg) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} ± \omega_J\Big) t \right) dt\]
En el límite del ensanchamiento Doppler muy pequeño, el\(\dfrac{\omega^2t^2kT}{2mc^2}\) factor puede ignorarse (es decir,\(\exp\bigg(- \dfrac{\omega^2t^2kT}{2mc^2}\bigg) \) establecer igual a la unidad), y
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp\bigg(-\dfrac{|t|}{\tau}\bigg) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} \pm \omega_J\Big) t \right) dt\]
resultados. Esta integral se puede realizar analíticamente y genera:
\[\frac{1}{4\pi}\left[\frac{1/\tau}{(1/\tau)^2+(\omega-\omega_{fv,iv} - \Delta E_{i,f}/\hbar ± \omega_J)^2} + \frac{1/\tau}{(1/\tau)^2+(\omega+\omega_{fv,iv} + \Delta E_{i,f}/\hbar ± \omega_J)^2} \right],\]
un par de picos lorentzianos en\(\omega\) -espacio centrado de nuevo en
\[\omega = ± [\omega_{fv,iv}+\Delta E_{i,f}/\hbar ± \omega_J].\]
El ancho completo a media altura de estos picos lorentzianos es\(2/\tau\). Se dice que los picos individuales se han ampliado de presión o colisionalmente.
Cuando no se puede descuidar el ensanchamiento Doppler en relación con el ensanchamiento colisional, la integral anterior
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp\bigg(-\dfrac{|t|}{\tau}\bigg) \exp\bigg(- \frac{\omega^2t^2kT}{2mc^2}\bigg) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} \pm \omega_J\Big) t \right) dt\]
es más difícil de realizar. Sin embargo, se puede llevar a cabo y nuevamente produce una serie de picos centrados en
\[\omega = \omega_{fv,iv}+\Delta E_{i,f}/\hbar ± \omega_J\]
pero cuyas anchuras están determinadas tanto por los efectos Doppler como por los efectos de ensanchamiento de presión. Por lo tanto, las formas de línea resultantes ya no son puramente lorentzianas ni gaussianas (que se comparan en la Figura 6.23 para ambas funciones que tienen el mismo ancho completo a media altura y la misma área integrada), sino que tienen una forma que se llama forma Voight.
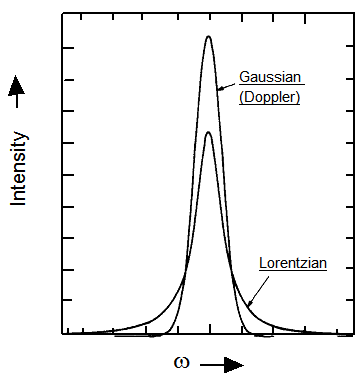
Las mediciones experimentales de anchos de línea que permiten extraer anchuras originadas por el ensanchamiento de colisiones proporcionan información (a través\(\tau\)) sobre la frecuencia de colisiones y la fuerza de estas colisiones. \(\tau\)Al determinar en una serie de densidades de gas, se puede separar la dependencia de la frecuencia de colisión y determinar la fuerza de las colisiones individuales (es decir, qué tan efectiva es cada colisión para reorientar el vector dipolo de la molécula).
Ampliamiento de Difusión Rotacional
Las moléculas en líquidos y gases muy densos experimentan colisiones tan frecuentes con las otras moléculas que el tiempo medio entre colisiones es corto en comparación con el período de rotación para su rotación sin obstáculos. Como resultado, la dependencia del tiempo de las funciones de correlación relacionadas con el dipolo ya no se puede modelar en términos de rotación libre que es interrumpida por colisiones (infrecuentes) y desplazamiento Doppler. En cambio, se vuelve apropiado un modelo que describa el incesante ataque del dipolo de la molécula por las moléculas circundantes. Para muestras líquidas en las que estas colisiones frecuentes hacen que el dipolo experimente movimientos angulares que cubren todos los ángulos (es decir, en contraste con un vidrio congelado o sólido en el que el dipolo de la molécula sufriría un movimiento pendular fuertemente perturbado alrededor de alguna orientación favorecida), la llamada difusión rotacional modelo se utiliza a menudo.
En esta imagen, la parte dependiente de la rotación de\(C(t)\) se expresa como:
\[\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle \]
\[= \langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,0) |\phi_J\rangle \exp( -2D_{\rm rot}|t|),\]
donde\(D_{\rm rot}\) esta la constante de difusión rotacional cuya magnitud detalla el tiempo
decaimiento en el valor promedio de\(\textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t)\) en el tiempo\(t\) con respecto a su valor en el tiempo\(t = 0\); cuanto mayor\(D_{\rm rot}\), más rápido es este decaimiento. Al igual que con el ensanchamiento de presión, esta dependencia exponencial del tiempo, cuando se somete a transformación de Fourier, produce:
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp( -2D_{\rm rot}|t|) \exp\bigg(- \frac{\omega^2t^2kT}{2mc^2}\bigg) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} \pm \omega_J\Big) t \right)\]
Nuevamente, en el límite del ensanchamiento Doppler muy pequeño, el\(\dfrac{\omega^2t^2kT}{2mc^2}\) factor puede ignorarse (es decir,\(\exp\bigg(- \dfrac{\omega^2t^2kT}{2mc^2}\bigg)\) establecer igual a la unidad), y
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp( -2D_{\rm rot}|t|) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} \pm \omega_J\Big) t \right)\]
resultados. Esta integral puede ser evaluada analíticamente y genera:
\[\frac{1}{4\pi}\left[\frac{2D_{\rm rot}}{(2D_{\rm rot})^2+(\omega-\omega_{fv,iv} - \Delta E_{i,f}/\hbar ± \omega_J)^2} + \frac{2D_{\rm rot}}{(2D_{\rm rot})^2+(\omega+\omega_{fv,iv} + \Delta E_{i,f}/\hbar ± \omega_J)^2} \right],\]
un par de picos lorentzianos en\(\omega\) -espacio centrado de nuevo en
\[\omega = ±[\omega_{fv,iv}+\Delta E_{i,f}/\hbar ± \omega_J].\]
El ancho completo a media altura de estos picos lorentzianos es\(4D_{\rm rot}\). En este caso, se dice que los picos individuales se han ampliado a través de la difusión rotacional. En tales casos, la medición experimental de anchos de línea arroja información valiosa sobre la rapidez con la que la molécula se difunde rotacionalmente en su ambiente condensado.
Ampliamiento homogéneo de por vida o Heisenberg
Siempre que la especie absorbente sufre uno o más procesos que agotan su número, decimos que tiene una vida finita. Por ejemplo, una especie que sufre disociación unimolecular tiene una vida finita, al igual que un estado excitado de una molécula que decae por emisión espontánea de un fotón. Cualquier proceso que agote la especie absorbente aporta otra fuente de dependencia del tiempo para las funciones de correlación de tiempo dipolo\(C(t)\) discutidas anteriormente. Esta dependencia del tiempo suele modelarse agregando, de manera multiplicativa, un factor\(\exp(-|t|/t)\). Esto, a su vez modifica la función de forma de línea de una\(I(\omega)\) manera muy parecida a la discutida al tratar el caso de difusión rotacional:
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp\bigg(-\dfrac{|t|}{\tau}\bigg) \exp\bigg(- \frac{\omega^2t^2kT}{2mc^2}\bigg) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} \pm \omega_J\Big) t \right) dt\]
No en vano, cuando la contribución Doppler es pequeña, se obtiene:
\[\frac{1}{4\pi}\left[\frac{1/\tau}{(1/\tau)^2+(\omega-\omega_{fv,iv} - \Delta E_{i,f}/\hbar ± \omega_J)^2} + \frac{1/\tau}{(1/\tau)^2+(\omega+\omega_{fv,iv} + \Delta E_{i,f}/\hbar ± \omega_J)^2} \right].\]
En estas líneas lorentzianas, el parámetro\(\tau\) describe la vida útil de decaimiento cinético de la molécula. Se dice que las líneas espectrales han sido de por vida o Heisenberg ampliadas en una cantidad proporcional a\(1/\tau\). Esta última terminología surge porque la vida finita de los estados moleculares puede ser vista como productora, a través de la relación de incertidumbre de Heisenberg\(\Delta E \Delta t \rangle \hbar\), estados cuya energía es incierta dentro de una cantidad\(\Delta E\).
Amplamiento no homogéneo del sitio
Entre los mecanismos de ampliación de la línea anterior, la presión, la difusión rotacional y los ensanchamientos de vida son todos de la variedad homogénea. Esto significa que todas y cada una de las moléculas de la muestra se ven afectadas exactamente de la misma manera por el proceso de ampliación. Por ejemplo, no se encuentran algunas moléculas con vidas cortas y otras con vidas largas en el caso Heisenberg; todo el conjunto de moléculas se caracteriza por una sola vida.
En contraste, el ensanchamiento Doppler es de naturaleza no homogénea porque cada molécula experimenta un ensanchamiento que es característico de su velocidad particular\(v_z\). Es decir, las moléculas rápidas tienen sus líneas ensanchadas más que las moléculas más lentas. Otro ejemplo importante de ensanchamiento no homogéneo es proporcionado por el llamado ensanchamiento del sitio. Las moléculas incrustadas en un líquido, sólido o vidrio no experimentan exactamente las mismas interacciones con su entorno en el instante de su absorción de fotones. La distribución de los entornos de solvatación instantánea puede ser bastante estrecha (por ejemplo, en una matriz sólida altamente ordenada) o bastante amplia (por ejemplo, en un líquido a alta temperatura o en un líquido supercrítico). Diferentes ambientes producen diferentes divisiones de nivel de energía\(\omega = \omega_{fv,iv}+\Delta E_{i,f}/\hbar ± \omega_J\) (porque los estados inicial y final están solvatados de manera diferente por el entorno) y, por lo tanto, diferentes frecuencias a las que puede ocurrir la absorción de fotones. La distribución de las divisiones del nivel de energía hace que la muestra se absorba en un rango de frecuencias como se ilustra en la Figura 6.24 donde se comparan formas de líneas homogéneas y no homogéneas.
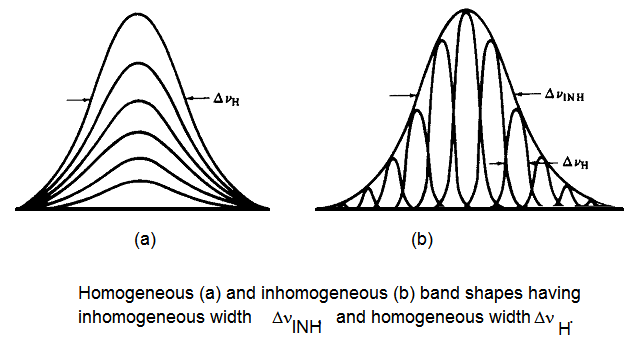
Por lo tanto, la función\(I(\omega)\) de forma de la línea espectral se amplía aún más cuando la inhomogeneidad del sitio está presente y es significativa. Estos efectos pueden modelarse convolucionando el tipo de\(I(\omega)\) función que resulta del Doppler, la vida útil, la difusión rotacional y el ensanchamiento de presión con una distribución gaussiana\(P(\Delta E)\) que describe la distribución no homogénea de las divisiones del nivel de energía:
\[I(\omega) = \int I^0(\omega,\Delta E)P(\Delta E)d\Delta E.\]
Aquí\(I^0(\omega;\Delta E)\) hay una función de forma de línea como las descritas anteriormente, cada una de las cuales contiene un conjunto de frecuencias (por ejemplo,\(\omega_{fv,iv}+\Delta E_{i,f}/\hbar ± \omega_J +\Delta E /\hbar = \omega+\Delta E /\hbar\)) en las que ocurre la absorción o emisión y\(P(\Delta E)\) es una función de probabilidad gaussiana que describe el ensanchamiento no homogéneo de la división de energía\(\Delta E\).
Una prueba experimental común para determinar si el ensanchamiento no homogéneo es significativo implica la quema de agujeros. En tales experimentos, una fuente de luz intensa (a menudo un láser) se sintoniza a una frecuencia\(\omega_{\rm burn}\) que se encuentra dentro de la línea espectral que se sondea para un ensanchamiento no homogéneo. Luego, con la fuente de luz intensa encendida constantemente, se utiliza una segunda fuente de luz sintonizable para escanear a través del perfil de la línea espectral, y se registra un espectro de absorción. Dado un perfil de absorción como se muestra en la Figura 6.25 en ausencia de la fuente de luz de combustión intensa:

se espera ver un perfil como el que se muestra en la Figura 6.26 si el ensanchamiento no homogéneo es operativo.

La interpretación del cambio en el perfil de absorción causado por la fuente de luz brillante procede de la siguiente manera:
- En el conjunto de moléculas contenidas en la muestra, algunas moléculas absorberán a o cerca de la frecuencia de la fuente de luz brillante\(\omega_{\rm burn}\); otras moléculas (aquellas cuyos ambientes no producen divisiones de nivel de energía que coincidan\(\omega_{\rm burn}\)) no absorberán a esta frecuencia.
- Aquellas moléculas que absorben a\(\omega_{\rm burn}\) voluntad tienen su transición saturada por la fuente de luz intensa, lo que hace que esta región de frecuencia del perfil lineal sea transparente para una mayor absorción.
- Cuando la fuente de luz de la sonda se escanea sobre el perfil lineal, inducirá absorciones para aquellas moléculas cuyos entornos locales no permitieron que fueran saturadas por la\(\omega_{\rm burn}\) luz. El perfil de absorción registrado por el detector de esta fuente de luz sonda coincidirá así con el del perfil de línea original, hasta
- La frecuencia de la fuente de luz de la sonda coincide\(\omega_{\rm burn}\), sobre lo cual no se registrará ninguna absorción de los fotones de la fuente de sonda debido a que las moléculas que absorben en este régimen de frecuencia han tenido su transición saturada.
- Por lo tanto, aparecerá un agujero en el espectro de absorción registrado por el detector de la fuente de luz de la sonda en la región de\(\omega_{\rm burn}\).
Desafortunadamente, la técnica de la quema de agujeros no proporciona un método completamente confiable para identificar líneas no homogéneamente ensanchadas. Si se observa un agujero en tal experimento de quema, esto proporciona una amplia evidencia, pero si no se ve uno, el resultado no es definitivo. En este último caso, la transición puede no ser lo suficientemente fuerte (es decir, puede no tener una tasa suficientemente grande de absorción de fotones) para que la fuente de luz intensa sature la transición en la medida necesaria para formar un agujero.
Espectroscopía de fotoelectrones
La espectroscopia fotoelectrónica (PES) es un tipo especial de espectroscopia electrónica. Utiliza luz visible o UV para excitar una molécula o ion a un estado final en el que se expulsa un electrón. En efecto, induce transiciones a estados finales en los que un electrón ha sido promovido a un llamado orbital continuo no unido. La mayoría de los experimentos de PES se llevan a cabo utilizando una fuente de luz de frecuencia fija (generalmente un láser). Los fotones de esta fuente, cuando son absorbidos, expulsan electrones cuya intensidad y energías cinéticas\(KE\) se miden luego. Restar los electrones\(KE\) de la energía del fotón\(h\nu\) da la energía de unión\(BE\) del electrón:
\[BE = h\nu - KE.\]
Si la muestra sometida al experimento PES tiene moléculas en una variedad de estados iniciales (por ejemplo, dos estados electrónicos o varios niveles vibratorio-rotacionales del estado electrónico básico) que tienen diversas energías de unión\(BE_k\), se observará una serie de picos correspondientes a electrones expulsados con un variedad de energías cinéticas\(KE_k\) como ilustra la Figura 6.27 y como la condición de balance energético requiere:
\[BE_k = h\nu - KE_k.\]
El pico de electrones detectados con la mayor energía cinética provino del estado más alto del progenitor, mientras que aquellos con baja energía cinética provinieron del estado de menor energía del progenitor.
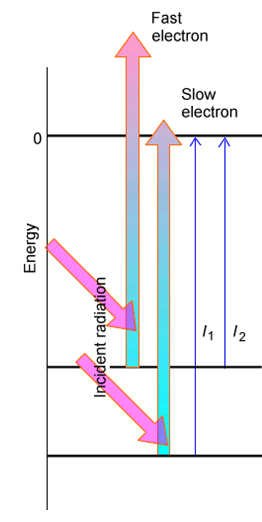
Al examinar los espaciamientos entre estos picos, se aprende sobre los espaciamientos entre los niveles de energía de la especie progenitora que ha sido sometida a pérdida de electrones.
Alternativamente, si la especie progenitora existe principalmente en su estado más bajo pero la especie hija producida cuando se retira un electrón del progenitor tiene estados excitados (electrónicos, vibración-rotación) a los que se puede acceder, se puede observar una progresión diferente de los picos. En este caso, los electrones con mayor energía cinética surgen de transiciones que conducen al estado de menor energía de la hija como ilustra la Figura 6.28. En esa figura, la superficie de energía inferior pertenece al padre y la curva superior a la hija.
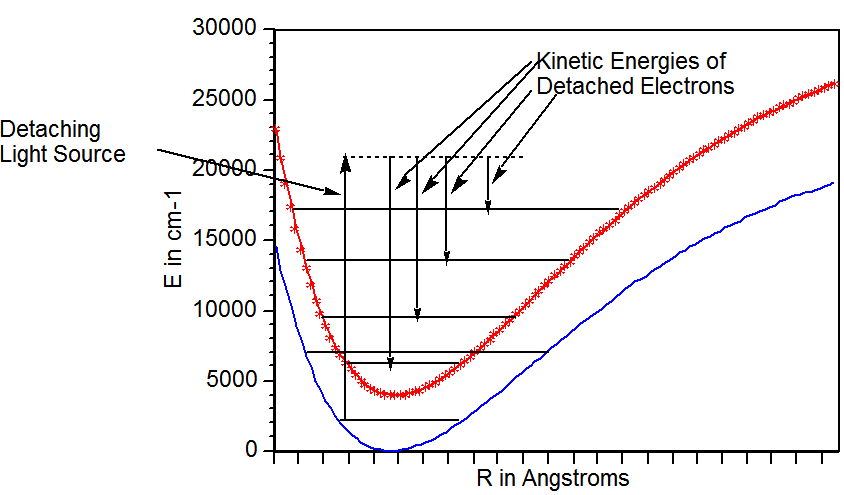
Un ejemplo de datos experimentales de fotodesprendimiento se proporciona en la Figura 6.29 que muestra la intensidad de los electrones detectados cuando el\(Cu_2^-\) anión pierde un electrón frente a la energía cinética de los electrones expulsados.
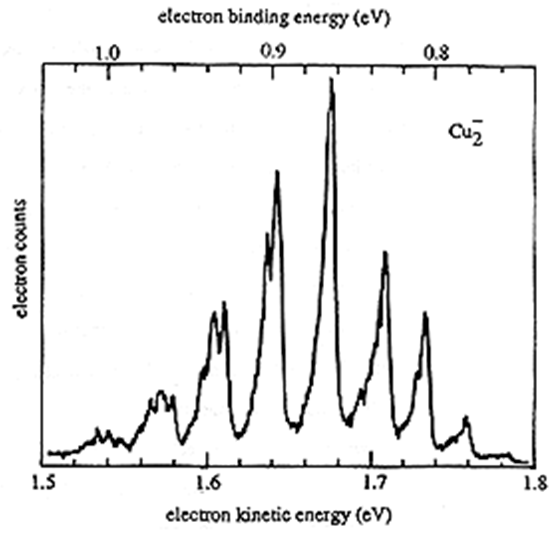
El pico a una energía cinética de ca. 1.54 eV, correspondiente a una energía de unión de 1.0 eV, surge de\(Cu_2^-\) la\(v=0\) pérdida de un electrón para producir\(Cu_2\) en\(v=0\). El pico más intenso corresponde a una\(v=4\) transición\(v=0\) a. Al igual que en el caso de la espectroscopia UV visible, los factores Franck-Condon que implican la superposición de las funciones de onda vibratoria\(Cu_2^-\) aniónica y\(Cu_2\) neutra gobiernan las intensidades relativas de los picos de PES.
Otro ejemplo se da en la Figura 6.30 donde aparece el espectro de fotodesprendimiento de\(H_2C=C^-\) (el anión del carbeno vinilideno).
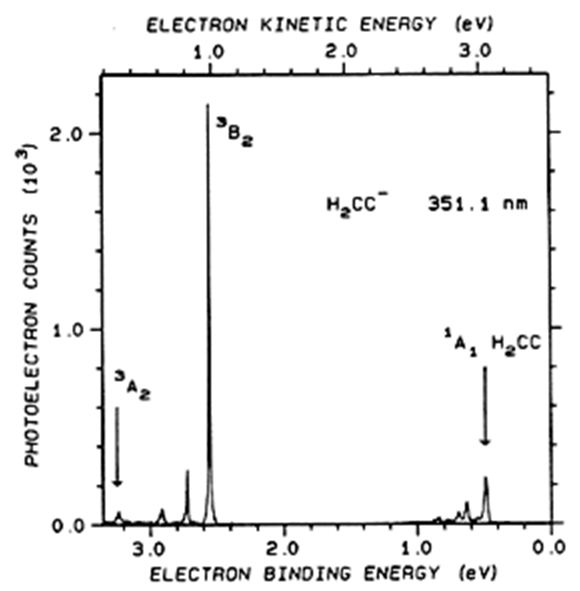
En este espectro, los picos que tienen energías de unión a electrones cercanas a 0.5 eV corresponden a transiciones en las que el estado fundamental\(H_2C=C^-\)\(v=0\) se separa para producir estado fundamental (\(^1A_1\))\(H_2C=C\) en varios niveles de v. Los espaciamientos entre este grupo de picos se relacionan con los espaciamientos en estados vibracionales de este estado\(^1A_1\) electrónico. La serie de picos con energías de unión cercanas a 2.5 eV corresponden a transiciones en las que\(H_2C=C^-\) se separa para producir\(H_2C=C\) en su estado electrónico\(^3B_2\) excitado. Los espaciamientos entre picos en este rango se relacionan con espaciamientos en estados vibracionales de este\(^3B_2\) estado. El espaciamiento entre los picos cercanos a 0.5 eV y aquellos cercanos a 2.5 eV se relaciona con la diferencia de energía entre los estados\(^1A_1\) electrónicos\(^3B_2\) y del neutro\(H_2C=C\).
Debido a que el PES ofrece una manera directa de medir las diferencias de energía entre las energías aniónicas y neutras o neutras y catiónicas, es un medio potente y ampliamente utilizado para determinar las afinidades moleculares de electrones (EA) y los potenciales de ionización (IPs). Debido a que los IP y los EA se relacionan, a través del teorema de Koopman, con las energías orbitales, se considera que PES es una forma de medir las energías orbitales. Sus envolventes vibracionales también ofrecen una buena manera de sondear los espaciamientos de los niveles de energía vibratoria y, por lo tanto, las fuerzas de unión.
Sondeo de Orbitales Continuum
Existe otro tipo de espectroscopia que se puede utilizar para sondear directamente los orbitales de una molécula que se encuentra en el continuo (es decir, a energías superiores a la del neutro parental). Le pido que reflexione de nuevo sobre nuestra discusión en el Capítulo 2 de los estados de tunelización y de resonancia que pueden ocurrir cuando un electrón experimenta potenciales tanto atractivos como repulsivos. En tales casos, existe una energía especial en la que el electrón puede quedar atrapado por el potencial atractivo y tener que atravesar la barrera repulsiva para finalmente escapar. Es este tipo de situaciones las que esta espectroscopía sondea.
Este experimento se denomina espectroscopía de transmisión de electrones (ETS). En tal experimento, se permite que un haz de electrones que tiene una intensidad conocida\(I_0\) y un rango de energías\(E\) cinéticas estrechamente definido pase a través de una muestra (generalmente gaseosa) de espesor\(L\). Se monitorea la intensidad\(I\) de los electrones que se observa que pasan a través de la muestra y llegan a un detector que se encuentra a lo largo de la dirección del haz incidente, al igual que las energías cinéticas de estos electrones\(E’\). Tal experimento se describe en forma cualitativa en la Figura 6.31.

Si las moléculas de la muestra tienen un orbital de resonancia cuya energía es cercana a la energía cinética\(E\) de los electrones colisionantes, es posible que un electrón del haz sea capturado en dicho orbital y exista en este orbital por un tiempo considerable. Por supuesto, ante la ausencia de colisiones u otros procesos para llevar el exceso de energía, este anión volverá a emitir un electrón en un momento posterior. De ahí que tales aniones se llamen metaestables y sus estados electrónicos se denominan estados de resonancia. Si el electrón capturado permanece en este orbital durante un período de tiempo comparable o más largo que el tiempo que tarda el anión molecular naciente en sufrir un movimiento vibracional o rotacional, pueden ocurrir varios eventos antes de que el electrón sea reemitido:
i.algunas longitudes o ángulos de enlace pueden cambiar (esto sucederá si el orbital ocupado por el electrón del haz tiene carácter de enlace o antienlace) por lo que, cuando el electrón se emite posteriormente, la molécula neutra queda con un cambio en la energía vibratoria;
ii.la molécula puede rotar, por lo que cuando se expulsa el electrón, no se emite en la misma dirección que el haz incidente.
En el primer caso, se observan electrones emitidos con energías\(E’\) que difieren de la del haz incidente en cantidades relacionadas con los niveles internos de energía vibratoria del anión. En esta última, se ve una reducción en la intensidad del haz que se transmite directamente a través de la muestra y electrones que se dispersan lejos de esta dirección.
Dicho espectro ETS se muestra en la Figura 6.32 para una muestra gaseosa de\(CO_2\) moléculas.
En este espectro, la energía de los electrones del haz transmitido se traza en el eje horizontal y la derivada de la intensidad del haz transmitido se grafica en el eje vertical. Es común trazar tales derivados en experimentos de tipo ETS para permitir identificar más claramente la variación de la señal con energía.
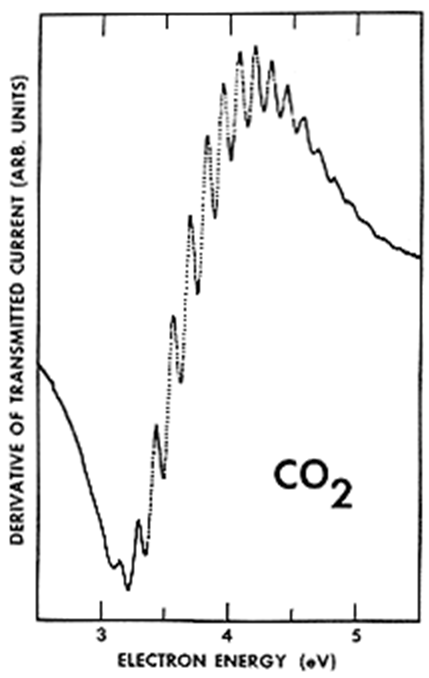
En este espectro ETS de\(CO_2\), las oscilaciones que aparecen dentro de la característica espectral principal mostrada (cuyo centro está cerca de 3.8 eV) corresponden a los niveles vibracionales de estiramiento y flexión del\(CO_2^-\) anión metaestable. Es la vibración de flexión la que se excita principalmente debido a que el electrón del haz ingresa al LUMO de\(CO_2\), que es un orbital de la forma mostrada en la Figura 6.33.
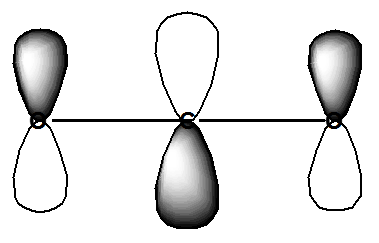
La ocupación de este\(\pi^*\) orbital antiadhesión, hace que ambos enlaces C-O se alarguen y que el ángulo O-C-O se doble lejos de 180 grados. La flexión permite reducir la naturaleza antiadhesión de este orbital.
Otros ejemplos de espectros ETS se muestran en la Figura 6.34.
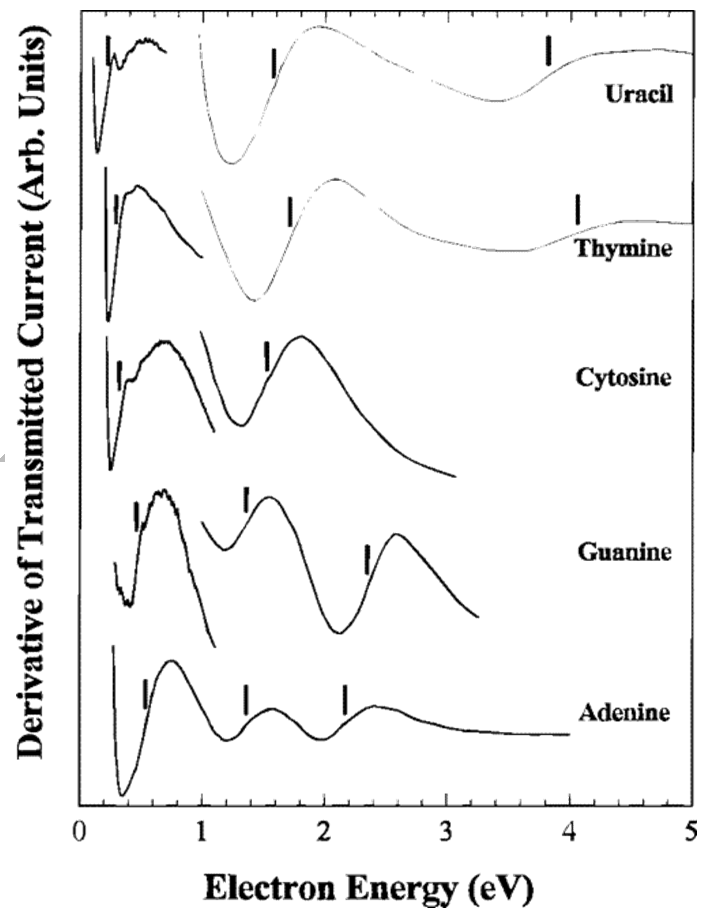
Aquí, nuevamente se muestra un espectro derivado, y se han agregado las líneas verticales para mostrar dónde pasa la derivada por cero, que es donde la señal de absorción ETS tendría un pico. Estos máximos corresponden a electrones que ingresan a diversos\(\pi^*\) orbitales virtuales de las moléculas base de uracilo y ADN. Es al encontrar estos picos en el espectro ETS que se pueden determinar las energías de tales orbitales continuos.
Antes de cerrar esta sección, es importante describir cómo se utiliza la teoría para simular los estados metaestables que surgen en dichos experimentos de ETS. Dichos cálculos no son en absoluto sencillos, y requieren la introducción de herramientas especiales diseñadas para modelar adecuadamente el continuo resonante orbital.
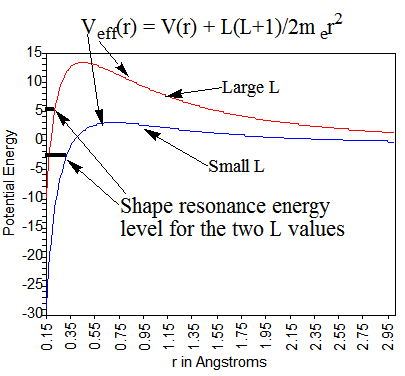
Para los aniones metaestables, es difícil aproximar el potencial experimentado por el exceso de electrones. Por ejemplo, los aniones de carga única en los que el exceso de electrón ocupa un orbital molecular\(\phi\) que posee un momento angular distinto de cero tienen potenciales efectivos como se muestra en la Figura 6.35, los cuales dependen del\(L\) valor de momento angular del orbital.
Por ejemplo, el\(\pi^*\) orbital de\(N_2^-\) mostrado en la Figura 6.36 produce dos contribuciones contrarias al potencial radial efectivo\(V_{\rm eff}(r)\) experimentado por un electrón que lo ocupa.
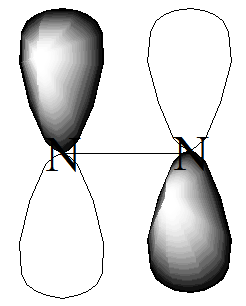
Primero, los dos centros de nitrógeno ejercen potenciales atractivos sobre el electrón en este orbital. Estas atracciones son más fuertes cuando el exceso de electrones está cerca de los núcleos, pero se descomponen rápidamente a grandes distancias porque las repulsiones de Coulomb de los otros electrones proyectan las atracciones nucleares. En segundo lugar, debido a que el orbital\(\pi^*\) molecular está compuesto por funciones de base atómica de\(p_{\pi}\)\(d_{\pi}\), etc. simetría, posee un momento angular distinto de cero. Debido a que la\(\pi^*\) órbita tiene simetría gerada, su carácter largo-r está dominado por el momento\(L = 2\) angular. Como resultado, el exceso de electrones tiene un potencial radial centrífugo\(L(L+1)/2m_er^2\) derivado en gran medida de su\(L = 2\) carácter.
Los atractivos potenciales de valencia de corto alcance\(V(r)\) y el potencial centrífugo se combinan para producir un potencial efectivo neto como se ilustra en la Figura 6.35. La energía de un electrón que experimenta tal potencial puede estar o no por debajo de la\(r \rightarrow \infty\) asíntota. Si el potencial atractivo es suficientemente fuerte, como lo es para\(O_2^{-1}\), el electrón en el\(\pi^*\) orbital se unirá y su energía quedará por debajo de esta asíntota. Por otro lado, si el potencial atractivo no es tan fuerte, como es el caso de los átomos de nitrógeno menos electronegativos en\(N_2^{-1}\), la energía del\(\pi^*\) orbital puede estar por encima de la asíntota. En estos últimos casos, se habla de estados de resonancia de forma metaestable. Son metaestables porque sus energías se encuentran por encima de la asíntota para que puedan descomponerse al hacer un túnel a través de la barrera centrífuga. Se les llama resonancias de forma porque su metaestabilidad surge de la forma de su barrera centrífuga repulsiva.
Si se tuviera a mano una aproximación razonable al atractivo potencial de corto alcance\(V(r)\) y se conociera la simetría L del orbital ocupado por el exceso de electrones, se podría formar\(V_{\rm eff}(r)\) como arriba. Sin embargo, para calcular la vida útil de la resonancia de la forma, hay que conocer la energía\(E\) de este estado. La herramienta más común y poderosa para estudiar dichos estados metaestables teóricamente es el método de estabilización (SM) que el profesor Howard Taylor de la USC fue pionero. Este método implica incrustar el sistema de interés (por ejemplo, el\(N_2^{-1}\) anión) dentro de una caja radial finita con el fin de convertir el continuo de estados correspondientes, por ejemplo, a\(N_2 + e^-\), en estados discretos que pueden manejarse usando métodos más convencionales. Al variar entonces el tamaño de la caja, se pueden variar las energías de los estados discretos que corresponden\(N_2 + e^-\) (es decir, se varía la energía cinética\(KE\) del orbital que contiene el exceso de electrones). A medida que se varía el tamaño de la caja, finalmente se nota (por ejemplo, trazando los orbitales) que uno de los\(N_2 + e^-\) estados posee una cantidad significativa de carácter de valencia (es decir, de corto alcance). Es decir, uno de esos estados tiene una amplitud significativa no sólo a grandes-r sino también en la región de los dos centros de nitrógeno. Es este estado el que corresponde al estado de resonancia de forma metaestable, y es la energía\(E\) donde se desarrollan componentes de valencia significativos la que proporciona la estimación de estabilización de la energía del estado.
Sigamos usando\(N_2^{-1}\) como ejemplo de cómo se emplearía el SM, especialmente cómo se suele variar la caja dentro de la cual se constriñe el anión. Se utilizaría un conjunto de bases orbitales atómicas convencionales que probablemente incluiría s y\(\pi\) funciones en cada\(N\) átomo, quizás algunas funciones de polarización d y algunos\(\pi\) orbitales difusos convencionales en cada\(N\) átomo. Estos orbitales de base sirven principalmente para describir los movimientos de los electrones dentro de las regiones de valencia habituales del espacio.
A esta base, se agregarían conjuntos adicionales de orbitales\(\pi\) de simetría difusa. Estos orbitales podrían ser\(p_\pi\) (y tal vez\(d_\pi\)) funciones centradas en cada átomo de nitrógeno, o podrían ser\(p_\pi\) (y tal vez\(d_\pi\)) orbitales centrados en el punto medio del enlace N-N. Por lo general, no se agregaría solo una de esas funciones; más bien se usarían varias funciones de este tipo, cada una con un exponente orbital\(\alpha_J\) que caracteriza su extensión radial. Supongamos, por ejemplo, que se han utilizado\(K\) tales\(\pi\) funciones.
A continuación, utilizando la base orbital atómica convencional así como las funciones de\(\pi\) base\(K\) extra, se realiza un cálculo (la mayoría de las veces un cálculo variacional en el que se calculan muchos niveles de energía) sobre el\(N_2^{-1}\) anión. En este cálculo, se tabulan las energías de muchos (digamos M) de los estados electrónicos de\(N_2^{-1}\). Por supuesto, debido a que se debe utilizar un conjunto de bases orbitales atómicas finitas, se encuentra un espectro discreto de energías orbitales y, por lo tanto, de energías de estado electrónico. Hay orbitales ocupados que tienen energía negativa que representan, vía. Teorema de Koopman, los estados ligados de la\(N_2^-\). También existen los llamados orbitales virtuales (es decir, aquellos orbitales que no están ocupados) cuyas energías se encuentran por encima de cero (es decir, no describen estados ligados). Estos últimos orbitales ofrecen una aproximación discreta al continuo dentro del cual se encuentra el estado de interés de resonancia.
Luego se escala los exponentes orbitales {\(\alpha_J\)} de los orbitales de\(\pi\) base\(K\) extra por un factor\(\eta\):\(\alpha_J \rightarrow \eta \alpha_J\) y repite el cálculo de las energías de las M energías más bajas de\(N_2^{-1}\). Esta escala hace que los orbitales de\(\pi\) base extra se contraigan radialmente (si\(\eta > 1\)) o se expandan radialmente (si\(\eta < 1\)). Es esta base de expansión y contracción orbital la que produce expansión y contracción de la caja comentada anteriormente. Es decir, no se emplea una caja directamente; en cambio, se varía la extensión radial de los orbitales de base más difusos para simular la variación de la caja.
Si la base orbital convencional es adecuada, se encuentra que los\(\pi\) orbitales adicionales, cuyos exponentes están siendo escalados, no afectan apreciablemente la energía de la\(N_2\) molécula neutra. Esto se puede sondear trazando la\(N_2\) energía como una función del parámetro de escalado h; si la energía varía poco con\(\eta\), la base convencional es adecuada.
En contraste con las gráficas de la\(N_2\) energía neutra vs.\(\eta\), las gráficas de las energías de los\(N_2^{-1}\) estados M muestran una dependencia h significativa como ilustra la Figura 6.37.
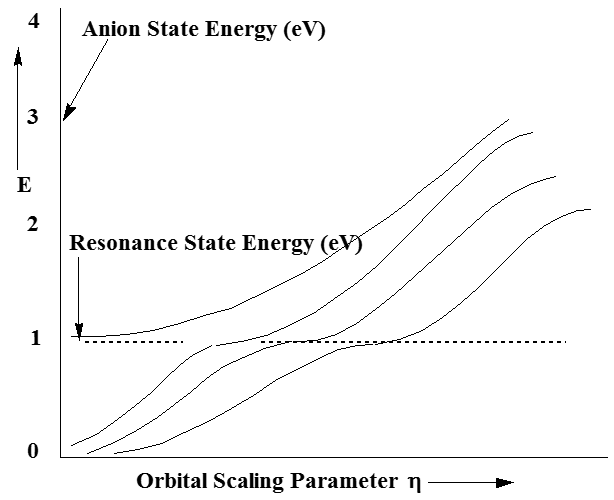
¿Qué nos dice esa trama de estabilización y qué significan las diversas ramas de la parcela? Primero, uno debe notar que cada una de las parcelas de la energía de un estado anión (relativa a la energía de la molécula neutra, que es independiente de\(\eta\)) crece con h cada vez mayor. Esta dependencia h surge de la escala h de los orbitales de\(\pi\) base extra difusa. Debido a que la mayor parte de la amplitud de tales orbitales base se encuentra fuera de la región de valencia, la energía cinética es el contribuyente dominante a la energía de tales orbitales. Debido a que\(\eta\) entra en cada orbital como\(\exp(-\eta \alpha r^2)\), y debido a que el operador de energía cinética involucra la segunda derivada con respecto a r, las energías cinéticas de los orbitales dominadas por las funciones de\(\pi\) base difusa varían como\(\eta^2\).
Para pequeños\(\eta\), todas las funciones de base\(\pi\) difusa tienen sus amplitudes concentradas a gran r y tienen baja energía cinética. Esto se debe a que, para pequeños\(\eta\) todos estos orbitales son muy difusos y concentran la densidad de electrones a grandes distancias. \(\eta\)A medida que crece, estas funciones se vuelven más compactas radialmente y sus energías cinéticas crecen. Por ejemplo, observe las tres energías más bajas mostradas arriba aumentando desde cerca de cero a\(\eta\) medida que crece.
A medida que aumenta\(\eta\) más, se llega a un punto en el que la tercera y cuarta energías de estado anión experimentan un cruce evitado. A este\(\eta\) valor, si se examina la naturaleza de las dos funciones de onda cuyas energías se evitan entre sí, se encuentra que una de ellas contiene cantidades sustanciales tanto de valencia como de carácter de\(\pi\) función extra-difusa. Justo a la izquierda del cruce evitado, el estado de menor energía (el tercer estado para pequeños\(\eta\)) contiene predominantemente carácter\(\pi\) orbital extra difuso, mientras que el estado de mayor energía (el cuarto estado) contiene en gran parte carácter\(\pi^*\) orbital de valencia.
Sin embargo, en el valor especial de\(\eta\) donde estos dos estados casi se cruzan, la energía cinética del tercer estado (así como su tamaño radial y su longitud de onda de Broglie) son apropiadas para conectarse adecuadamente con el cuarto estado. Por conectar correctamente queremos decir que los dos estados tienen amplitudes de función de onda, fases y pendientes que coinciden. Entonces, a este\(\eta\) valor especial, se puede lograr una descripción del estado de forma-resonancia que describa correctamente este estado tanto en la región de valencia como en la región largo-r. Solo ajustando la energía de los estados largo-r usando el\(\eta\) escalado se puede obtener esta coincidencia de condición de límite adecuada.
En resumen, al realizar una serie de cálculos de energía de estado anión para varios estados y trazarlos vs.\(\eta\), se obtiene una gráfica de estabilización. Al examinar esta gráfica y buscar cruces evitados, se pueden identificar las energías a las que ocurren las resonancias metaestables. También es posible utilizar las formas (es decir, la magnitud de la división de energía entre los dos estados y las pendientes de las dos curvas evitadas) de los cruces evitados en una gráfica de estabilización para calcular las vidas de los estados metaestables. Básicamente, cuanto mayor sea la división de energía de cruce evitada entre los dos estados, más corta es la vida útil del estado de resonancia.
Entonces, los experimentos ETS y PES ofrecen maravillosas sondas de los estados unidos y continuos de moléculas e iones que nos dicen mucho sobre la naturaleza electrónica y la unión química de estas especies. El estudio teórico de estos fenómenos se complica por la necesidad de identificar y describir adecuadamente los orbitales y estados continuos que estén involucrados. La técnica de estabilización nos permite lograr una buena aproximación a los estados de resonancia que se encuentran en dicha continua.
Colaboradores y Atribuciones
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


