2.1: Teoría de Probabilidad Discreta
- Page ID
- 71889
Variables aleatorias discretas
Considera un ensayo\(\mathcal{T}\) donde la observación es una medida del\(z\) componente\(\hbar m_S\) del momento angular de giro de un giro\(S = 5/2\). Solo hay seis posibles resultados (eventos) que pueden ser etiquetados con el número cuántico de espín magnético\(m_S\) o indexados por números enteros 1, 2,\(\ldots\) 6. En general, las probabilidades de los seis eventos posibles serán diferentes entre sí. Dependerán de la preparación y pueden depender del tiempo de evolución antes de la observación. Para describir tales situaciones, definimos un conjunto de eventos elementales
\[A = \left\{ a_j \right\} \ ,\]
donde en nuestro ejemplo el índice\(j\) va del 1 al 6, mientras que en general va del 1 al número\(N_A\) de eventos posibles. A cada uno de los eventos se le asigna una probabilidad\(0 \leq P(a_j) \leq 1\). Los eventos imposibles (para una preparación dada) tienen probabilidad cero y un determinado evento tiene probabilidad 1. Dado que uno y sólo uno de los eventos debe ocurrir en cada ensayo, las probabilidades se normalizan,\(\sum_j^{N_A} P(a_j) = 1\). Un modelo simplificado de nuestro ensayo de ejemplo es el enrollado de un dado. Si el dado es justo, tenemos la situación especial de una distribución uniforme de probabilidad, es decir,\(P(a_j) = 1/6\) para todos\(j\).
Un conjunto de eventos aleatorios con sus probabilidades asociadas se llama variable aleatoria. Si el número de eventos aleatorios es contable, la variable aleatoria se llama discreta. En una computadora, se pueden asignar números a los eventos, lo que hace que la variable aleatoria sea un número aleatorio. Luego se puede simular una serie de ensayos generando una serie de números\(\mathcal{N}\) pseudoaleatorios que asignan los eventos observados en los\(\mathcal{N}\) ensayos. Tales simulaciones se llaman simulaciones de Monte Carlo. Los números pseudoaleatorios obtenidos de una función de computadora necesitan ser ajustados para que reproduzcan las probabilidades dadas o asumidas de los eventos. [concepto:random_variable]
Usando la función rand de Matlab, que proporciona números aleatorios distribuidos uniformemente en el intervalo abierto\((0,1)\), escriba un programa que simule lanzar un dado con seis caras. La función externa debe tener el número de prueba\(\mathcal{N}\) como entrada y un vector de los números de los encontrados, dos,... y sejes como salida. Debe basarse en una función interna que simule un solo lanzamiento del dado. Pruebe el programa determinando la diferencia con respecto a la expectativa\(P(a_j) = 1/6\) para un número cada vez mayor de ensayos.
Múltiples variables aleatorias discretas
Para dos conjuntos de eventos\(A\)\(B\) y sus probabilidades, definimos una probabilidad conjunta\(P(a_j,b_k)\) que es la probabilidad de observar ambos\(a_j\) y\(b_k\) en el mismo ensayo. Un ejemplo es el lanzamiento de dos dados, uno negro y otro rojo, y preguntar sobre la probabilidad de que el dado negro muestre un 2 y el rojo muere un 3. Un ejemplo un poco más complicado es la medición de los\(z\) componentes individuales del momento angular de giro de dos giros acoplados\(S_\mathrm{A} = 5/2\) y\(S_\mathrm{B} = 5/2\). Al igual que las probabilidades individuales, las probabilidades conjuntas caen en el intervalo cerrado\([0,1]\). Las probabilidades de las articulaciones se normalizan,
\[\sum_a \sum_b P(a,b) = 1 \ .\]
Tenga en cuenta que hemos introducido una breve notación que suprime índices\(j\) y\(k\). Esta notación se encuentra a menudo por su conveniencia en la escritura.
Si conocemos las probabilidades\(P(a,b)\) para todas las combinaciones\(N_A \cdot N_B\) posibles de los dos eventos, podemos calcular la probabilidad de un solo evento, por ejemplo\(a\),
\[P_A(a) = \sum_b P(a,b) \ ,\]
donde\(P_A(a)\) está la probabilidad marginal de evento\(a\).
El desafortunado término 'marginal' no implica una probabilidad pequeña. Históricamente, estas probabilidades se calcularon en los márgenes de las tablas de probabilidad.
Otra cantidad de interés es la probabilidad condicional\(P(a|b)\) de un evento\(a\), siempre y cuando eso\(b\) haya sucedido. Por ejemplo, si llamamos a dos cartas de un mazo completo, la probabilidad de que la segunda carta sea una Reina está condicionada a que la primera carta haya sido Reina. Con la definición para la probabilidad condicional tenemos
\[\begin{align} P(a,b) & = P(a|b) P_B(b) \\ & = P(b|a) P_A(a) \ .\end{align}\]
Si la probabilidad marginal de evento no\(b\) es cero, la probabilidad condicional de evento\(a\) dada\(b\) es
\[\begin{align} & P(a|b) = \frac{P(b|a) P_A(a)}{P_B(b)} \ . \label{eq:Bayes_Theorem}\end{align}\]
El teorema de Bayesian es la base de la inferencia bayesiana, donde\(a\) se busca la probabilidad de proposición dado el conocimiento previo (corto: el previo)\(b\). Muchas veces la probabilidad bayesiana se interpreta subjetivamente, es decir, diferentes personas, por tener diferentes conocimientos previos\(b\), llegarán a diferentes valoraciones para la probabilidad de proposición\(a\). Esta interpretación es incompatible con la física teórica, donde, con bastante éxito, se asume una realidad objetiva. La teoría de probabilidad bayesiana también se puede aplicar con una interpretación objetiva en mente y hoy en día se utiliza, entre otras cosas, en la modelización estructural de biomacromoléculas para evaluar la concordancia de un modelo (la proposición) con datos experimentales (el anterior).
En la física experimental, la biofísica y la química física, el teorema de Bayes se puede utilizar para asignar probabilidades informadas experimentalmente a diferentes modelos de realidad. Por ejemplo, supongamos que un enfoque de modelado teórico, por ejemplo una simulación MD, ha proporcionado un conjunto de conformaciones\(A = \{ a_j \}\) de una molécula de proteína y probabilidades asociadas\(P_A(a_j)\). Las probabilidades están relacionadas, a través de la distribución de Boltzmann, con las energías libres de las conformaciones (este punto se discute más adelante en el curso de la conferencia). Además, asumimos que tenemos una medición\(B\) con salida\(b_k\) y conocemos la probabilidad marginal\(P_B(b)\) de encontrar esta salida para un conjunto aleatorio de conformaciones de la molécula de proteína. Entonces solo necesitamos un modelo físico que proporcione las probabilidades condicionales\(P(b_k|a_j)\) de medir\(b_k\) dadas las conformaciones\(a_j\) y pueda calcular la probabilidad de\(P(a_j|b_k)\) que la conformación verdadera sea\(a_j\), dado el resultado de nuestra medición, a través del teorema de Bayes. Ecuación\ ref {EQ:Bayes_Theorem}). Este procedimiento puede generalizarse a múltiples mediciones. Los requeridos\(P(b_k|a_j)\) dependen de errores de medición. El enfoque permite combinar modelos posiblemente conflictivos y resultados experimentales para llegar a una 'mejor estimación' para la distribución de conformaciones.
Los eventos asociados a dos variables aleatorias pueden ocurrir completamente independientes entre sí. Este es el caso de lanzar dos dados: el número que se muestra en el dado negro no depende del número que se muestre en el dado rojo. De ahí que la probabilidad de observar un 2 en el negro y un 3 en el dado rojo es\((1/6)\cdot(1/6) = 1/36\). En general, las probabilidades conjuntas de eventos independientes factorizan en las probabilidades individuales (o marginales), lo que lleva a grandes simplificaciones en los cálculos. En el ejemplo de dos espines acoplados\(S_\mathrm{A} = 5/2\) y\(S_\mathrm{B} = 5/2\) las dos variables aleatorias\(m_{S,\mathrm{A}}\) y\(m_{S,\mathrm{B}}\) pueden o no ser independientes. Esto se decide por la fuerza del acoplamiento, la preparación del ensayo\(\mathcal{T}\) y el tiempo de evolución\(t\) antes de la observación.
Si dos variables aleatorias son independientes, la probabilidad conjunta de dos eventos asociados es el producto de las dos probabilidades marginales,
\[\begin{align} & P(a,b) = P_A(a) P_B(b) \ .\end{align}\]
Como consecuencia, la probabilidad condicional\(P(a|b)\) es igual a la probabilidad marginal de\(a\) (y viceversa),
\[\begin{align} & P(a|b) = P_A(a) \ .\end{align}\]
[concepto:variables_independientes]
Para un conjunto de más de dos variables aleatorias se pueden establecer dos grados de independencia, un tipo débil de independencia por pares y un tipo fuerte de independencia mutua. El conjunto es mutuamente independiente si la distribución de probabilidad marginal en cualquier subconjunto, es decir, el conjunto de probabilidades marginales para todas las combinaciones de eventos en este subconjunto, viene dada por el producto de las distribuciones marginales correspondientes para los eventos individuales. 2 Esto corresponde a la independencia completa. La menor independencia por pares implica que las distribuciones marginales para cualquier par de variables aleatorias están dadas por el producto de las dos distribuciones correspondientes. Tenga en cuenta que puede existir una independencia aún más débil dentro del conjunto, pero no en todo el conjunto. Algunos, pero no todos los pares o subconjuntos de variables aleatorias pueden exhibir independencia.
Otro concepto importante para múltiples variables aleatorias es si son o no distinguibles. En el ejemplo anterior usamos un dado negro y otro rojo para especificar nuestros eventos. Si ambos dados fueran negros, las combinaciones de eventos\((a_2,b_3)\) y\((a_3,b_2)\) serían indistinguibles y el evento compuesto correspondiente de observar un 2 y un 3 tendría una probabilidad de\(1/18\), es decir, el producto de la probabilidad\(1/36\) del evento compuesto básico con su multiplicidad 2. En general, si las variables\(n\) aleatorias son indistinguibles, la multiplicidad es igual al número de permutaciones de las\(n\) variables, que es\(n! = 1\cdot 2\cdots (n-1)\cdot n\).
Funciones de Variables Aleatorias Discretas
Consideramos un evento\(g\) que depende de otros dos eventos\(a\) y\(b\). Por ejemplo, pedimos la probabilidad de que esté la suma de los números mostrados por el dado negro y rojo\(g\), donde\(g\) puede oscilar entre 2 y 12, dado que conocemos las probabilidades\(P(a,b)\), que en nuestro ejemplo todas tienen el valor 1/36. En general, la distribución de probabilidad de la variable aleatoria\(G\) puede calcularse mediante
\[P_G(g) = \sum_a \sum_b \delta_{g,G(a,b)} P(a,b) \ , \label{eq:fct_rand_var}\]
donde\(G(a,b)\) es una función arbitraria de\(a\) y\(b\) y el delta de Kronecker\(\delta_{g,G(a,b)}\) asume el valor uno si\(g = G(a,b)\) y cero en caso contrario. En nuestro ejemplo,\(g = G(a,b) = a+b\) asumirá el valor de 5 para las combinaciones de eventos\((1,4),(2,3),(3,2),(4,1)\) y ninguna otra. De ahí,\(P_G(5) = 4/36 = 1/9\). Solo hay una sola combinación para\(g=2\), por lo tanto\(P_G(2) = 1/36\), y hay 6 combinaciones para\(g=7\), por lo tanto\(P_G(7) = 1/6\). Aunque las distribuciones de probabilidad para los números aleatorios individuales\(A\) y\(B\) son uniformes, la de no lo\(G\) es. Se alcanza su punto máximo en el valor de\(g=7\) que tiene más realizaciones. Tal pico de distribuciones de probabilidad que dependen de múltiples variables aleatorias ocurre con mucha frecuencia en la mecánica estadística. Los picos tienden a volverse más agudos cuanto mayor es el número de variables aleatorias que contribuyen a la suma. Si este número\(N\) tiende al infinito, la distribución de la suma\(g\) es tan nítida que el ancho de distribución (que se especificará a continuación) es menor que el error en la medición del valor medio\(g/N\) (ver Sección [section:prob_dist_sum]). Este efecto es la esencia misma de la termodinámica estadística: Aunque las cantidades para una sola molécula pueden estar ampliamente distribuidas e impredecibles, el valor medio para un gran número de moléculas, digamos\(10^{18}\) de ellas, está muy bien definido y perfectamente predecible.
En un programa informático numérico, la ecuación\ ref {eq:fct_rand_var}) para solo dos variables aleatorias se puede implementar muy fácilmente por un bucle sobre todos los valores posibles de\(g\) con bucles internos sobre todos los valores posibles de\(a\) y\(b\). Dentro del bucle más interno,\(G(a,b)\) se calcula y se compara con el índice de bucle\(g\) para agregar o no agregar\(P(a,b)\) al bin correspondiente al valor\(g\). Sin embargo, tenga en cuenta que tal enfoque no lleva a grandes números de variables aleatorias, ya que el número de bucles anidados aumenta con el número de variables aleatorias y el tiempo de cálculo aumenta exponencialmente. Los cálculos analíticos se simplifican por el hecho de que\(\delta_{g,G(a,b)}\) generalmente se desvía de cero solo dentro de ciertos rangos de los índices de suma\(j\) (for\(a\)) y\(k\) (for\(b\)). El truco es entonces encontrar las combinaciones adecuadas de rangos de índice.
Calcular la distribución de probabilidad para la suma\(g\) de los números mostrados por dos dados de dos maneras. Primero, escribe un programa de computadora usando el enfoque esbozado anteriormente. Segundo, computar la distribución de probabilidad analíticamente haciendo uso de la distribución uniforme para los eventos individuales (\(P(a,b) = 1/36\)para todos\(a,b\). Para ello, considere rangos de índice que conduzcan a un valor dado de la suma\(g\). 3
Distribuciones de probabilidad discretas
En la mayoría de los casos, las variables aleatorias se comparan considerando los valores medios y anchuras de sus distribuciones de probabilidad. Como medida del ancho, se utiliza la desviación estándar\(\sigma\) de los valores del valor medio, que es la raíz cuadrada de la varianza\(\sigma^2\). El concepto puede generalizarse considerando funciones\(F(A)\) de la variable aleatoria. En las siguientes expresiones, se\(F(A) = A\) proporciona el valor medio y la desviación estándar de la variable aleatoria original\(A\).
Para cualquier función\(F(A)\) de una variable aleatoria\(A\), el valor medio\(\langle F \rangle\) viene dado por,
\[\begin{align} & \langle F \rangle = \sum_a F(a) P_A(a) \ .\end{align}\]
La desviación estándar, que caracteriza el ancho de la distribución de los valores de la función\(F(a)\), viene dada por,
\[\begin{align} & \sigma = \sqrt{\sum_a \left( F(a) - \langle F \rangle \right)^2 P_A(a)} \ .\end{align}\]
El valor medio es el primer momento de la distribución, definiéndose el\(n^\mathrm{th}\) momento por
\[\langle F^n \rangle = \sum_a F^n(a) P_A(a) \ .\]
El momento\(n^\mathrm{th}\) central es
\[\langle \left( F - \langle F \rangle \right)^n \rangle = \sum_a \left( F(a) - \langle F \rangle \right)^n P_A(a) \ .\]
Para la varianza, que es el segundo momento central, tenemos
\[\sigma^2 = \langle F^2 \rangle - \langle F \rangle^2 \ .\]
Supongamos que conocemos los valores medios para funciones\(F(A)\) y\(G(B)\) de dos variables aleatorias así como el valor medio\(\langle F G \rangle\) de su producto, que podemos calcular si\(P(a,b)\) se conoce la función de probabilidad conjunta. Luego podemos calcular una función de correlación
\[R_{FG} = \langle F G \rangle - \langle F \rangle \langle G \rangle \ ,\]
que toma el valor de cero, si\(F\) y\(G\) son números aleatorios independientes.
Ejercicio\(\PageIndex{1}\)
Calcular la distribución de probabilidad para la suma normalizada\(g/M\) de los números obtenidos al lanzar\(M\) dados en una sola prueba. Comience con\(M=1\) y continúe vía\(M=10, 100, 1000\) a\(M = 10000\). Descubre cuántos ensayos de Monte Carlo\(\mathcal{N}\) necesitas para adivinar la distribución convergente. ¿Cuál es el valor medio\(\langle g/M \rangle\)? ¿Cuál es la desviación estándar\(\sigma_g\)? ¿De qué dependen\(\mathcal{N}\)?
Distribución de probabilidad de una suma de números aleatorios
Si asociamos los números aleatorios con\(N\) moléculas, idénticas o no, a menudo necesitaremos calcular la suma sobre todas las moléculas. Esto genera un nuevo número aleatorio
\[S = \sum_{j=1}^N F_j \ ,\]
cuyo valor medio es la suma de los valores medios individuales,
\[\langle S \rangle = \sum_{j=1}^N \langle F_j \rangle \ .\]
Si el movimiento de las moléculas individuales no está correlacionado, los números aleatorios individuales\(F_j\) son independientes. Entonces se puede demostrar que las varianzas suman,
\[\sigma_S^2 = \sum_{j=1}^N \sigma_j^2\]
Para moléculas idénticas, todos los números aleatorios tienen la misma media\(\langle F \rangle\) y varianza\(\sigma_F^2\) y encontramos
\[\begin{align} \langle S \rangle & = N \langle F \rangle \\ \sigma_S^2 & = N \sigma_F^2 \\ \sigma_S & = \sqrt{N} \sigma_F \ .\end{align}\]
Este resultado se relaciona con el concepto de pico de distribuciones de probabilidad para un gran número de moléculas que se introdujo anteriormente en el ejemplo de la distribución de probabilidad para la suma de los números mostrados por dos dados. El ancho de la distribución normalizado a su valor medio,
\[\frac{\sigma_S}{\langle S \rangle} = \frac{1}{\sqrt{N}} \frac{\sigma_F}{\langle F \rangle} \ ,\]
escalas con la raíz cuadrada inversa de\(N\). Para\(10^{18}\) las moléculas, este ancho relativo de la distribución es mil millones de veces menor que para una sola molécula. Supongamos que para una cierta cantidad física de una sola molécula la desviación estándar es tan grande como el valor medio. No se puede hacer ninguna predicción útil. Para una muestra macroscópica, se puede predecir la misma cantidad con una precisión mejor que la precisión que se puede esperar en una medición.
Distribución binomial
Consideramos la medición del\(z\) componente del momento angular de giro para un conjunto de\(N\) giros\(S = 1/2\). 4 El número aleatorio asociado a un giro individual puede tomar solo dos valores,\(-\hbar/2\) o\(+\hbar/2\). Las constantes aditivas y multiplicativas pueden ser atendidas por separado y así podemos representar cada giro por un número aleatorio\(A\) que asume el valor\(a=1\) (for\(m_S = +1/2\)) con probabilidad\(P\) y, en consecuencia, el valor\(a=0\) (for\(m_S = -1/2\)) con probabilidad\(1-P\). Se trata de un problema muy general, que también se relaciona con el segundo postulado de Penrose (ver Sección [Penrose_postulados]). Una versión simplificada con\(P = 1-P = 0.5\) viene dada por\(N\) volteretas de una moneda justa. Una moneda justa o una moneda sesgada con se\(P \neq 0.5\) puede implementar fácilmente en una computadora, por ejemplo usando a = floor (Rand+p) en Matlab. Para los números aleatorios individuales encontramos\(\langle A \rangle = P\) y\(\sigma_A^2 = P(1-P)\), de manera que la desviación estándar relativa para el conjunto con\(N\) miembros se convierte en\(\sigma_S/\langle S \rangle = \sqrt{(1-P)/(N \cdot P)}\). 5
Para calcular la distribución de probabilidad explícita de la suma de los números aleatorios para todo el conjunto, nos damos cuenta de que la probabilidad de que un subconjunto de miembros del\(n\) conjunto proporcione un 1 y los miembros del\(N-n\) conjunto proporcionen un 0 es\(P^n(1-P)^{N-n}\). El valor de la suma asociada a esta probabilidad es\(n\).
Ahora todavía hay que considerar el fenómeno ya encontrado para la suma de los números en los dados negros y rojos: Diferentes números\(n\) tienen multiplicidades diferentes. Tenemos\(N!\) permutaciones de los miembros del conjunto. Asignemos un 1 a los primeros\(n\) miembros de cada permutación. Para nuestro problema, no importa en qué secuencia se numeren estos\(n\) miembros y no importa en qué secuencia se numeren\(N-n\) los miembros restantes. Por lo tanto, necesitamos dividir el número total de permutaciones entre\(N!\) los números de permutaciones en cada subconjunto,\(n!\) y\((N-n)!\) para el primer y segundo subconjunto, respectivamente. La multiplicidad que necesitamos es el número de combinaciones de\(N\) elementos a la\(n^\mathrm{th}\) clase, que así viene dada por el coeficiente binomial,
\[\binom {N} {n} = \frac{N!}{n!(N-n)!} \ , \label{eq:N_over_n}\]
proporcionar la distribución de probabilidad
\[P_S(n) = \binom {N} {n} P^n(1-P)^{N-n} \ .\]
Para grandes valores de\(N\) la distribución binomial tiende a una distribución gaussiana,
\[G(s) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left[-\frac{(s-\langle s \rangle)^2}{2 \sigma^2}\right] \ .\]
Como ya sabemos el valor medio\(\langle s \rangle = \langle n \rangle = N P\) y varianza\(\sigma_S^2 = N P (1-P)\), podemos anotar inmediatamente la aproximación
\[P_S(n) \approx \frac{1}{\sqrt{2 \pi P(1-P)N}} \exp\left[-\frac{(n-PN)^2}{2P(1-P)N} \right] = G(n) \ .\]
Como se muestra en\(\PageIndex{1}\) la Figura, la aproximación gaussiana de la distribución binomial es bastante buena ya en\(N = 1000\).
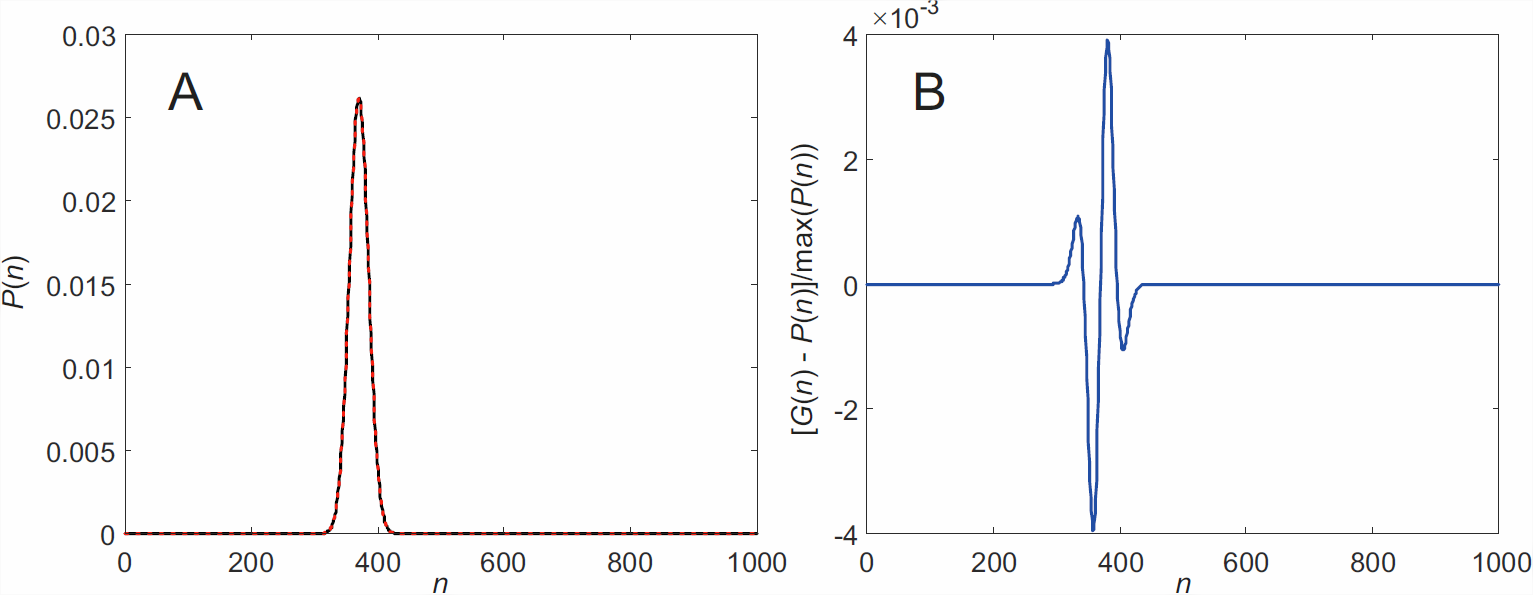
De hecho, la distribución gaussiana (o normal) es una distribución general para la media aritmética de un gran número de variables aleatorias independientes:
Supongamos que se ha hecho un gran número\(N\) de observaciones con cada observación correspondiente a un número aleatorio que es independiente de los números aleatorios de las otras observaciones. Según el teorema del límite central, el valor medio\(\langle S \rangle/N\) de la suma de todos estos números aleatorios se distribuye aproximadamente normalmente, independientemente de la distribución de probabilidad de los números aleatorios individuales, siempre que todas las distribuciones de probabilidad de todos los individuos los números aleatorios son idénticos. 6 Se aplica el teorema del límite central, si cada variable aleatoria individual tiene un valor medio bien definido (valor de expectativa) y una varianza bien definida. Estas condiciones se cumplen para ensayos estadísticamente regulares\(\mathcal{T}\). [concepto:central_limit_teorema]
Fórmula de Stirling
El número\(N!\) de permutaciones aumenta muy rápido con\(N\), lo que lleva a desbordamiento numérico en calculadoras y computadoras a valores\(N\) que corresponden a nanoclusters más que a muestras macroscópicas. Incluso los coeficientes binomiales, que crecen menos fuertemente al aumentar el tamaño del conjunto, no se pueden calcular con una precisión razonable para\(N \gg 1000\). Además, el factorial\(N!\) es difícil de manejar en el cálculo. El problema de escalado puede resolverse tomando el logaritmo del factorial,
\[\ln N! = \ln \left( \prod_{n=1}^N n \right) = \sum_{n=1}^N \ln n \ .\]
Para grandes números,\(N\) el logaritmo natural del factorial se puede aproximar por la fórmula de Stirling
\[\begin{align} & \ln N! \approx N \ln N - N + 1 \ , \label{eq:Stirling}\end{align}\]
que equivale a la aproximación
\[\begin{align} & N! \approx N^N \exp(1-N)\end{align}\]
para el factorial mismo. Para grandes números\(N\) es posible además descuidar 1 en la suma y aproximado\(\ln N! \approx N \ln N - N\).
El error absoluto de esta aproximación para\(N!\) parece bruto y aumenta rápido con el aumento\(N\), pero debido a que\(N!\) crece mucho más rápido, el error relativo se vuelve insignificante ya a moderado\(N\). Porque\(\ln N!\) se aproxima de cerca por\(-0.55/N\). De hecho, Gosper ha encontrado una aproximación aún mejor,
\[\ln N! \approx N \ln N - N + \frac{1}{2} \ln\left[\left(2N+\frac{1}{3}\right)\pi\right] \ .\]
La aproximación de Gosper es útil para considerar sistemas de tamaño moderado, pero tenga en cuenta que varios de nuestros otros supuestos y aproximaciones se vuelven cuestionables para dichos sistemas y hay que tener mucho cuidado en la interpretación de los resultados. Para los sistemas macroscópicos, en los que estamos principalmente interesados aquí, la fórmula de Stirling suele ser suficientemente precisa y no se necesita la de Gosper.
Un poco mejor que la fórmula original de Stirling, pero aún así una simple aproximación es
\[N! \approx \sqrt{2 \pi N} \left( \frac{N}{e} \right)^N \ . \label{eq:Stirling_better}\]

