4.4: Aplicando las Leyes de Probabilidad

Última actualización
Guardar como PDF

Page ID: 75191

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Las leyes de probabilidad se aplican a eventos que son independientes. Si el resultado de un juicio depende del resultado de otro juicio, es posible que aún podamos usar las leyes de probabilidad. No obstante, para ello, debemos conocer la naturaleza de la interdependencia.

Si la actividad asociada al evento C precede a la actividad asociada con el evento D, la probabilidad de D puede depender de si ocurre C. Supongamos que la primera actividad es lanzar una moneda y que la segunda actividad es sacar una carta de una baraja; sin embargo, la baraja que usemos depende de si la moneda sube de cabeza o de cola. Si la moneda es cabezas, sacamos una carta de una baraja ordinaria; si la moneda es colas, sacamos una moneda de una baraja con las cartas de la cara retiradas. Ahora nos preguntamos sobre la probabilidad de dibujar un as. Si la moneda es cabezas, la probabilidad de dibujar un as es\({4}/{52}={1}/{13}\). Si la moneda es colas, la probabilidad de dibujar un as es\({4}/{40}={1}/{10}\). La combinación de monedas es cabezas y carta es as tiene probabilidad:\(\left({1}/{2}\right)\left({1}/{13}\right)={1}/{26}\). La combinación de monedas es colas y carta es as tiene probabilidad\(\left({1}/{2}\right)\left({1}/{10}\right)={1}/{20}\). En este

caso, la probabilidad de dibujar un as depende de la modificación que hagamos a la baraja en función del resultado del lanzamiento de la moneda.

Aplicar las leyes de probabilidad es sencillo. Un ejemplo que ilustra la aplicación de estas leyes de manera transparente lo proporcionan los pueblos Primero, Segundo, Tercero y Cuarto, que están separados por ríos. (Ver Figura 1.) Puentes\(1\)\(2\),, y\(3\) abarcan el río entre Primera y Segunda. Puentes\(a\) y\(b\) abarcan el río entre la Segunda y la Tercera. Puentes\(A\),\(B\),\(C\), y\(D\) abarcan el río entre la Tercera y la Cuarta. Un viajero de Primera a Cuarta que sea libre de tomar cualquier ruta que le plazca tiene la opción de elegir entre\(3\times 2\times 4=24\) posibles combinaciones. Consideremos las probabilidades asociadas a diversos eventos:

Hay 24 rutas posibles. Si un viajero elige su ruta al azar, la probabilidad de que tome alguna ruta en particular es\({1}/{24}\). Esto ilustra nuestra suposición de que cada evento en un conjunto de eventos\(N\) exhaustivos y mutuamente excluyentes ocurre con probabilidad\({1}/{N}\).
Si elige una ruta al azar, la probabilidad de que vaya de Primera a Segunda ya sea por puente\(1\) o puente\(2\) es\(P\left(1\right)+P\left(2\right)=\ {1}/{3}+{1}/{3}={2}/{3}\). Esto ilustra el cálculo de la probabilidad de eventos alternativos.
La probabilidad de la ruta particular\(2\to a\to C\) es\(P\left(2\right)\times P\left(a\right)\times P\left(C\right)=\left({1}/{3}\right)\left({1}/{2}\right)\left({1}/{4}\right)={1}/{24}\), y calculamos la misma probabilidad para cualquier otra ruta de Primera a Cuarta. Esto ilustra el cálculo de la probabilidad de un evento compuesto.
Si cruza puente\(1\), la probabilidad de que su ruta sea\(2\to a\to C\) es cero, claro. La probabilidad de un evento que ya ocurrió es 1, y la probabilidad de cualquier alternativa es cero. Si cruza puente\(1,\)\(P\left(1\right)=1\), y\(P\left(2\right)=P\left(3\right)=0\).
Dado que un viajero ha utilizado puente\(1\), la probabilidad de la ruta\(1\to a\to C\) se convierte en la probabilidad de camino\(a\to C\), que es\(P\left(a\right)\times P\left(C\right)=\left({1}/{2}\right)\left({1}/{4}\right)={1}/{8}\). Ya que\(P\left(1\right)=1\), la probabilidad del evento compuesto\(1\to a\to C\) es la probabilidad del evento compuesto\(a\to C\).

Los resultados de rodar dados, rodar proporcionan más ilustraciones. Si tiramos dos dados, podemos clasificar los posibles resultados de acuerdo con las sumas de los resultados para los dados individuales. Hay treinta y seis posibles resultados. Se muestran en la Tabla 1.

Tabla 1: Resultados de lanzar dos dados

	Resultado para el primer dado
Resultado para el segundo dado		1	2	3	4	5	6
	1	2	3	4	5	6	7
	2	3	4	5	6	7	8
	3	4	5	6	7	8	9
	4	5	6	7	8	9	10
	5	6	7	8	9	10	11
	6	7	8	9	10	11	12

Consideremos las probabilidades asociadas con diversos eventos de lanzamiento de dados:

La probabilidad de cualquier resultado dado, digamos que el primer dado muestra\(2\) y el segundo dado muestra\(3\), es\({1}/{36}\).
Dado que la probabilidad de que se muestre el primer dado\(3\) mientras que el segundo dado muestra también lo\(2\) es\({1}/{36}\), la probabilidad de que un dado muestre\(2\) y el otro muestre\(3\) es\[P\left(3\right)\times P\left(2\right)+P\left(2\right)\times P\left(3\right) =\left({1}/{36}\right)+\left({1}/{36}\right) ={1}/{18}.\]
Cuatro resultados diferentes corresponden al evento en el que se encuentra el puntaje\(5\). Por lo tanto, la probabilidad de rodar\(5\) es\[P\left(1\right)\times P\left(4\right)+P\left(2\right)\times P\left(3\right) +P\left(3\right)\times P\left(2\right)+P\left(4\right)\times P\left(1\right) ={1}/{9}\]
La probabilidad de rodar una puntuación de tres o menos es la probabilidad de rodar\(2\), más la probabilidad de rodar\(3\) que es\(\left({1}/{36}\right)+\left({2}/{36}\right)={3}/{36}={1}/{12}\)
Supongamos que tiramos los dados uno a la vez y que el primer dado muestra\(2\). La probabilidad de rodar\(7\) cuando se lanza el segundo dado es ahora\({1}/{6}\), porque solo rodar a\(5\) puede hacer que el marcador sea 7, y existe la probabilidad de\({1}/{6}\) que a\(5\) suba cuando se lanza el segundo dado.
Supongamos que el primer dado es rojo y el segundo dado es verde. La probabilidad de que aparezca el dado rojo\(2\) y que aparezca el dado verde\(3\) es\(\left({1}/{6}\right)\left({1}/{6}\right)={1}/{36}\).

Arriba analizamos el número de resultados asociados con una puntuación de\(3\) para encontrar que la probabilidad de este evento es\({1}/{18}\). Podemos usar otro argumento para obtener este resultado. La probabilidad de que dos dados lanzan una puntuación de tres es igual a la probabilidad de que el primer dado muestre\(1\) o\(2\) veces la probabilidad de que el segundo dado muestre cualquier puntaje que sea necesario para que el total sea igual a tres. Esto es:

\[\begin{align*} P\left(first\ die\ shows\ 1\ or\ 2\right)\times \left({1}/{6}\right) &= \left[\left({1}/{6}\right)+\left({1}/{6}\right)\right]\times {1}/{6} \\[4pt] &={2}/{36} \\[4pt]& ={1}/{18} \end{align*}\]

La aplicación de las leyes de probabilidad se facilita frecuentemente al reconocer una simple reafirmación del requisito de que los eventos sean mutuamente excluyentes. En un juicio dado, o ocurre un suceso o no ocurre. Sea la probabilidad de que ocurra un evento\(P\left(A\right)\) A. Que la probabilidad de que no ocurra el evento A sea\(P\left(\sim A\right)\). Ya que en cualquier juicio dado, el resultado debe pertenecer ya sea al evento A o al evento\(\sim A\), tenemos

\[P\left(A\right)+P\left(\sim A\right)=1\]

Por ejemplo, si la probabilidad de éxito en un solo ensayo es\({2}/{3}\), la probabilidad de fracaso es\({1}/{3}\). Si consideramos los resultados de dos ensayos sucesivos, podemos agruparlos en cuatro eventos.

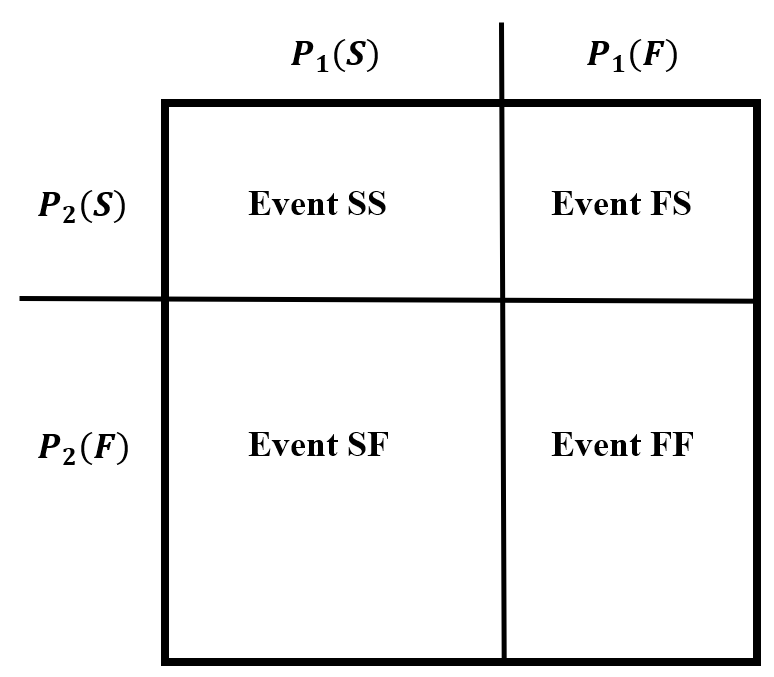
Evento SS: El primer juicio es un éxito; el segundo juicio es un éxito.
Evento SF: El primer juicio es un éxito; el segundo juicio es un fracaso.
Evento FS: El primer juicio es un fracaso; el segundo juicio es un éxito.
Evento FF: El primer juicio es un fracaso; el segundo juicio es un fracaso.

Usando las leyes de probabilidad, tenemos

\[ \begin{align*} 1 &=P\left(Event\ SS\right)+P\left(Event\ SF\right)+P\left(Event\ FS\right)+\ P(Event\ FF) \\[4pt] &=P_1\left(S\right)\times P_2\left(S\right)+P_1\left(S\right)\times P_2\left(F\right) +P_1(F)\times P_2(S)+P_1(F)\times P_2(F) \end{align*}\]

donde\(P_1\left(X\right)\) y\(P_2\left(X\right)\) son la probabilidad de suceso\(X\) en los ensayos primero y segundo, respectivamente.

Esta situación se puede mapear en un diagrama simple. Representamos los posibles resultados del primer ensayo por segmentos de línea en un lado de una unidad cuadrada\(P_1\left(S\right)+P_1\left(F\right)=1\). Representamos los resultados del segundo ensayo por segmentos de línea a lo largo de un lado contiguo de la unidad cuadrada. Los cuatro posibles eventos ahora están representados por las áreas de cuatro porciones mutuamente excluyentes y exhaustivas del cuadrado unitario como se muestra en la Figura 2.

Figura 2. Éxito y fracaso en ensayos sucesivos.