4.5: Combinatoria y Multiplicidad

Definiciones

Combinatoria: una rama de las matemáticas que se ocupa de las reglas para combinar diferentes resultados y eventos y calcular las probabilidades de estas combinaciones.

Probabilidad: La probabilidad de un resultado es una medida de la probabilidad de que el resultado ocurra en comparación con todos los resultados posibles.

Permutación: una “forma” en la que todo o parte de un conjunto de objetos puede ordenarse u ordenarse.

Combinación: una “forma” de seleccionar todo o parte de un conjunto de objetos sin tener en cuenta el orden en que se seleccionan los objetos.

Multiplicidad: la multiplicidad de eventos es el número total de “formas” en las que posiblemente pueden ocurrir diferentes resultados. Representado por el símbolo W, y también llamado vías, permutaciones, secuencias, degeneración, peso, arreglos, probabilidad termodinámica, etc. dependiendo del contexto.

Como se puede ver en estas definiciones, la combinatoria es la rama de la matemática relacionada con el conteo de eventos y resultados, mientras que la multiplicidad es la variable termodinámica estadística igual al número de posibles resultados. Están intrincadamente conectados.

Dependiendo de la situación, este número de posibles resultados (multiplicidad) podría calcularse utilizando los principios fundamentales de conteo, fórmulas de permutación o fórmulas de combinación del campo de la combinatoria. A continuación se muestra una explicación detallada y un ejemplo de cada uno de estos métodos de conteo y cuándo se pueden aplicar.

Los Principios Fundamentales del Conteo

El principio de multiplicación

Durante la semana del restaurante, sales a comer a cenar. El menú de la semana del restaurante te da la opción de elegir entre tres aperitivos, cuatro platos principales y dos postres. Te sientes un poco abrumado por la cantidad de posibilidades; ¿cuántas opciones de comida diferentes hay?

• Cada uno de estos eventos de selección tiene un número diferente de posibles resultados u opciones:
  • Selección de aperitivo = 3 opciones
  • Selección de entrada = 4 opciones
  • Evento de postre = 2 opciones
• Debido a que elegirás un aperitivo Y un plato principal Y un postre, el número total de diferentes formas de preparar tu comida es:\[W=3 \times 4 \times 2=24\]
• Uno de los Principios Fundamentales del Conteo, el Principio de Multiplicación establece que si hay n posibles resultados para cada tipo de evento, i, en una secuencia, entonces el número total de resultados posibles es igual a los valores de n multiplicados juntos:\[W=n_{1} n_{2} \cdots n_{t}=\prod_{i=1}^{t} n_{i}\] donde\(\prod\) símbolo es el operador del producto ( similar al\(\sum\) símbolo para el operador de suma).
• En este contexto, cada uno\(n_i\) representa el número de posibles resultados para cada evento. Por lo tanto, la multiplicidad de cada tipo de evento\(W_i\),, es igual a\(n_i\), y la multiplicidad total\(W_{t o t a l}\),, puede ser determinada por:\[W_{t o t a l}=W_{1} W_{2} \cdots W_{3}=\prod_{i=1}^{t} W_{i}\]

El principio de adición

Estás buscando comprar una carpeta nueva para guardar tus notas de clase. Estás entre una carpeta de 1" y una carpeta de 1.5”. La carpeta de 1” viene en 5 colores y la carpeta de 1.5” viene en 3. ¿Cuántas opciones totales de encuadernación está considerando?

• Cada una de las dos carpetas tiene un número diferente de posibles resultados:
  • Carpeta de 1” = 5 resultados
  • Carpeta de 1.5” = 3 resultados
• Debido a que elegirá una carpeta de 1” O una carpeta de 1.5”, el número total de diferentes resultados que está considerando es:\[W=5+3=8\]
• Uno de los Principios Fundamentales del Conteo, el Principio de Adición establece que si hay n posibles resultados para cada evento, i, y no podemos hacer ambos al mismo tiempo, entonces el número total de posibles resultados es igual a los valores de n sumados juntos:\[W=n_{1}+n_{2}+n_{3} \cdots=\sum_{i=1}^{t} n_{i}\]

Permutaciones

Permutaciones de resultados distinguibles sin repetición: TODOS los resultados seleccionados

¡Tú decides asumir el reto de probar cada uno de los 40 sabores de batidos de CookOut! Si tienes un batido diferente cada día hasta que los hayas probado todos (¡sin repeticiones!) , ¿cuántas secuencias diferentes de batidos (es decir, órdenes o arreglos) son posibles?

• Ya que no estás repitiendo ningún batido durante este tiempo, elegirás entre 40 batidos el día uno Y 39 el día dos Y 38 el día tres, etc. De acuerdo con el Principio de Multiplicación anterior, el número total de secuencias es:\[W=40 \times 39 \times 38 \times 37 \times \cdots \times 2 \times 1=40 !=8.16 \times 10^{47}\]
• El orden de los batidos importa en esta pregunta pero no se repiten batidos; esto se llama permutación sin repetición:\[W=N !\] dónde\(N\) está el número total de resultados posibles y todos se muestrean los posibles resultados (es decir, seguirás seleccionando batidos hasta que hayas probado todos los batidos). Debido a que puedes identificar qué batido estás probando cada día, los resultados u opciones se consideran distinguibles.

Permutaciones de resultados distinguibles sin repetición: solo algunos resultados

Pensándolo bien, tener un batido diferente todos los días durante 40 días puede ser un poco demasiado... En cambio, decides tomar un batido diferente todos los días durante una semana. (¡Entonces tomarás un descanso y volverás a abordar el resto del menú en el futuro!) ¿Cuántos arreglos o secuencias diferentes son posibles durante la primera semana?

• La matemática es similar a la pregunta anterior, excepto que solo necesitamos multiplicar los primeros siete de los números en el factorial para los primeros siete días:\[W=40 \times 39 \times 38 \times 37 \times 36 \times 35 \times 34=93963542400\]
• Una expresión más general para esta permutación sin repetición incluye el número total de resultados posibles, N, y el número total de eventos de selección, r, que se expresa como “\(N\), take\(r\)” (o tal vez quiera pensar en it as “\(N\), arrange\(r\)”):\[W=\ _{N}P_{r}=\frac{N !}{(N-r) !}\] donde\( _{N}P_{r}\) es una notación común para la permutación sin repetición.
• Para nuestro ejemplo, este sería:\[W={ }_{40} P_{7}=\frac{40 !}{(40-7) !}=\frac{40 !}{33 !}=\frac{40 \times 39 \times 38 \times 37 \times 36 \times 35 \times 34 \times 33 !}{33 !}=93963542400\]
• El ejemplo anterior (con los 40 batidos) también se puede representar de esta manera, sin embargo, ya que todos los elementos son seleccionados,\(N\) y\(r\) son iguales:\[W={ }_{40} P_{40}=\frac{40 !}{(40-40) !}=\frac{40 !}{0 !}=40!\]

Permutaciones de resultados distinguibles con repetición

Para ayudarte a superar las finales, decides tomar un batido todos los días durante la semana de finales, pero no te vas a molestar en probar otras diferentes; ¡solo puedes decidir tener el mismo todos los días! ¿Cuál sería el número total de secuencias de batidos en este caso?

• Si todos los días tienes la opción de 40 batidos diferentes, el número de secuencias posibles es:\[W=40 \times 40 \times 40 \times 40 \times 40 \times 40 \times 40=40^{7}=163840000000\]
• Esta es una permutación con repetición, y la ecuación da el número de secuencias posibles para r eventos que cada uno tiene N posibles resultados:\[W=N^{r}\]
• El término repetición indica que un resultado u objeto no se elimina del grupo disponible después de la selección. Otra forma de referirse a este concepto es como permutación con reemplazo; después de seleccionar un resultado en particular, ese resultado se devuelve al pool de selección para que las opciones de selección disponibles sean siempre las mismas.

Permutaciones de resultados indistinguibles

Durante las vacaciones de invierno, compras una bolsa de 11 oz de Holiday Milk Chocolate Hershey's Kisses. En la bolsa de 72 besos, tienes 25 besos rojos, 23 plateados y 24 verdes. Si sacas los besos de la bolsa uno a la vez, ¿cuántas secuencias diferentes de colores navideños son posibles?

• Puede parecer que esta descripción también se refiere a calcular el número de permutaciones para los elementos que se repiten (ya que hay múltiples besos de cada color envoltorio), y de hecho, algunos recursos sí hacen referencia a la ecuación de esa manera. Sin embargo, este escenario no se repite de la misma manera que el ejemplo anterior.
  • El término repetición se utiliza para una serie de eventos o conjunto de objetos donde se permite que los resultados se repitan después de haber sido seleccionados (es decir, el grupo de selección no cambia porque el resultado seleccionado es reemplazado por otro resultado del mismo tipo).
  • En el escenario actual, los besos individuales seleccionados no se “repiten” porque no se devuelven a la bolsa; a medida que se retira cada beso, el pool de selección disponible disminuye. En cambio, simplemente hay varios elementos indistinguibles en el grupo de selección antes de que comiencen las selecciones. Esto hace una diferencia en cuanto a cuántos artículos de cada tipo (es decir, besos de cada color) están disponibles para ser seleccionados.
• Si nuestros besos fueran etiquetados para que cada beso fuera distinguible de los demás, entonces nuestro número total de permutaciones se calcularía como se describió anteriormente:\[W=72 !\] Sin embargo, este cálculo contará\(red_A\) seguido de\(red_B\) como una secuencia diferente a la\(red_B\) seguida de\(red_A\) . Estos dos resultados son indistinguibles sin las etiquetas A y B, por lo que el número de secuencias únicas debe determinarse factorizando el número de arreglos idénticos o redundantes.
• El número de arreglos posibles para cada tipo individual de beso es:\[n_{r e d} =25 !\]\[n_{s i l v e r} =23 ! \]\[n_{g r e e n} =24 !\] Por lo tanto, nuestro número de secuencias o arreglos únicos es:\[W=\frac{N !}{n_{red} ! n_{silver} ! n_{green} !}=\frac{72 !}{25 ! 23 ! 24 !}\]
• Otra forma de referirse a este tipo de permutación es una permutación multiconjunto porque el conjunto general está compuesto por subconjuntos más pequeños de resultados indistinguibles. La expresión general para una permutación multiconjunto es:\[W=\frac{N !}{n_{1} ! n_{2} ! \cdots n_{t} !}\] donde cada uno\(n_i\) es el número de resultados posibles para cada tipo de selección\(i\), y el número total de resultados u objetos,\(N\), es:\[N=\sum_{i=1}^{t} n_{i}\]

Combinaciones

Combinaciones sin repetición

En el semestre de primavera, decides que ya has tenido suficientes batidos CookOut por un tiempo. ¡En su lugar compras helado Blue Bell en la tienda de abarrotes! Usted tiene 5 sabores: galletas y crema (CC), chispas de chocolate de menta (M), fresa (S), chocolate holandés (DC) y pudín de plátano (B). Si siempre obtienes tres bolas de diferentes sabores, ¿cuántas combinaciones diferentes son posibles?

• Vamos a enumerar nuestros cinco sabores disponibles de helado:

Supongamos que elegimos B para la primera primicia. Si no podemos tener cada sabor más de una vez (es decir, sin repetición), entonces B ya no es una opción para las primicias restantes. Por lo tanto, la segunda primicia solo tiene cuatro opciones disponibles:

Elegimos S para la segunda cucharada, y la retiramos de los sabores disponibles:

Por último, elegimos DC para la tercera primicia:

• Hasta ahora, este proceso parece una permutación sin repeticiones, y la ecuación de permutación produciría:\[{ }_{5} P_{3}=\frac{5 !}{(5-3) !}=\frac{5 !}{2 !}=5 \times 4 \times 3=60\]

Sin embargo, la combinación {B, S, DC} es indistinguible de otras combinaciones de B, S y DC recolectadas en un orden diferente. Una vez en el bol, el orden no importa. La ecuación de permutación contaría cada secuencia de B, S y DC por separado, por lo que necesitamos corregir el número de combinaciones duplicadas o indistinguibles.

Podemos ilustrar más este punto observando el ejemplo de B, S y DC con más detalle:

Hay seis secuencias distinguibles que producen combinaciones indistinguibles. También podríamos calcular este valor usando la permutación sin repetición para el número de primicias:\[\ _{3} P_{3}=\frac{3 !}{(3-3) !}=\frac{3 !}{0 !}=3 !=6\]

• Para determinar el número de combinaciones únicas o distinguibles (donde el orden no importa), necesitamos dividir nuestro número de secuencias distinguibles por el número de secuencias que producen combinaciones indistinguibles:\[W=\frac{60}{6}=10\]\[W=\frac{ _{5} P_{3}}{3 !}=\frac{\frac{5 !}{(5-3) !}}{3 !}=\frac{5 !}{(5-3) ! 3 !}=\frac{5 !}{2 ! 3 !}=10\]
• La ecuación general para esta combinación sin repetición, que se conoce como “\(N\), elige\(r\)” (o en nuestro caso “5 sabores de helado, elige 3”) es:

\ [W=\ _ {N} C_ {r} =\ izquierda (\ begin {array} {l}
N\\
r
\ end {array}\ derecha) =\ frac {_ {N} P_ {r}} {r!} =\ frac {N!} {(N-r)! r!} \]

donde\(\ _{N} C_{r}\) y\ (\ left (\ begin {array} {l}
N\\
r
\ end {array}\ right)\) son notaciones comunes para la combinación sin repetición.

Combinaciones con repetición

En lugar de hacer siempre tres bolas diferentes, ¿cuántas combinaciones diferentes son posibles si incluyes repeticiones (es decir, combinaciones con más de una cucharada de un sabor particular)?

• Este concepto se llama combinación con repetición o combinación con reemplazo. En este caso, es más fácil pensarlo como reemplazo.

Volvamos a enumerar nuestros cinco sabores de helado:

Supongamos que elegimos B para la primera primicia. Sin embargo, a diferencia de antes, después de que B haya sido tomado de los sabores disponibles, lo reemplazaremos por otro B, dejando las opciones de selección iguales:

Elegimos una segunda primicia de B a continuación, reemplazándola de nuevo por otra B:

Por último, elegimos DC para la última primicia:

• Lo que puedes ver es que, si tienes repeticiones o reemplazos, no terminas con “5, elige 3”. En cambio, debido a los reemplazos después de las dos primeras primicias, tuviste 7 opciones totales disponibles durante el proceso de selección, haciendo “7, elige 3”. \[W=\ _{7} C_{3}=\frac{7 !}{4 ! 3 !}=35\]
• Al considerar esto de manera más general, ojalá puedas reconocer que, independientemente del número de\(N_initial\) opciones con las que empezaste, si permites reemplazos, terminarás sumando opciones\((r-1)\) adicionales (una menos que el número de selecciones) por tu elección final. Su número final de opciones disponibles, por lo tanto, se convierte en:\[N_{\text {final}}=N_{\text {initial}}+(r-1)\] Podemos tomar esta expresión para el número final de opciones disponibles y sustituirla en la fórmula de combinación del ejemplo anterior:\[\ _{N} C_{r}=\frac{N !}{(N-r) ! r !}=\frac{N_{\text {final}} !}{\left(N_{\text {final}}-r\right) ! r !}=\frac{\left(N_{\text {initial}}+(r-1)\right) !}{\left(N_{\text {initial}}+(r-1)-r\right) ! r !}=\frac{\left(N_{\text {initial}}+(r-1)\right) !}{\left(N_{\text {initial}}-1\right) ! r !}\] Podemos reorganizar esta ecuación como:\ [\ left (\ left (\ begin {array} {l}
  N \\
  r
  \ end {array}\ right)\ right) =\ frac {\ left (\ left (\ left (N_ {\ text {initial}} -1\ right) +r\ right)!} {\ left (N_ {\ text {inicial}} -1\ derecha)! r!} \] donde la notación\ (\ left (\ left (\ begin {array} {l}
  N\\
  r
  \ end {array}\ right)\ right)\ right)\) se usa para denotar una combinación con reemplazo y se llama “\(N\), multichoose”\(r\).
• Esta nueva expresión se asemeja a una permutación para dos ítems con resultados indistinguibles: hay resultados\((N_{\text {initial}}-1)\) indistinguibles de un ítem y\(r\) del otro. Aquí es de donde viene la representación línea/punto.

Desarrollaremos el sistema como teniendo\((N_{\text {initial}}-1 )\) líneas y\(r\) puntos. Por lo tanto, para nuestros 5 sabores de helado y 3 bolas, usaremos 4 líneas y 3 puntos:\[W=\frac{(4+3) !}{4 ! 3 !}=35\]

• Si bien esta ecuación da la respuesta correcta, aún puede parecer extraño reformular el problema de esta manera. Veamos una vez más: finge que tenías una máquina de recolección de helados, y le diste instrucciones a esta máquina en un código de líneas y puntos. Cada punto representa una cucharada de helado, y cada línea separa (o divide) un sabor de otro. Para comunicar la combinación de {B, B, DC} a la máquina, envía el siguiente código (recordar que el orden no importa):

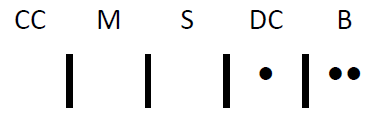
Si quisieras {CC, M, DC}, sería:

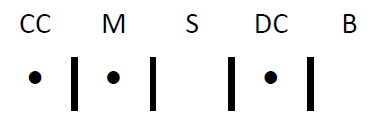
Y si querías todo CC:

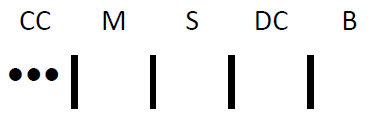
Para demostrar que el método línea/punto funciona de manera general, reconozca que, para\(N_{\text {initial}}\) las opciones, siempre habrá\((N_{\text {initial}}-1 )\) líneas necesarias para separarlas entre sí. Para\(r\) las opciones, siempre necesitarás un total de\(r\) puntos, uno para cada elección. ¡Funciona para usar tres puntos colocados entre cuatro líneas que separan los cinco sabores!

Por lo tanto\(N\), la combinación “, multichoose\(r\)” con ecuación de reemplazo es igual a la ecuación de permutación para\((N_{\text {initial}}-1 )\) líneas y\(r\) puntos, donde las líneas y puntos son indistinguibles:\ [\ left (\ left (\ begin {array} {l}
N\\
r
\ end {array}\ right)\ right) = {} _ {N-1} P_ {r} =\ frac {((N-1) +r)!} {(N-1)! r!} \]