6.5: Más sobre Teoría Molecular Cinética

Objetivos de aprendizaje

Asegúrese de comprender a fondo las siguientes ideas esenciales que se presentan a continuación. Es especialmente importante que conozcas los significados precisos de todos los términos en cursiva en el contexto de este tema.

• Debería poder esbozar la forma general de la gráfica de Maxwell-Boltzmann mostrando la distribución de las velocidades moleculares. También se debe mostrar cómo estas parcelas se ven afectadas por la temperatura y por la masa molar.
• Si bien no es necesario que puedas derivar la ecuación de estado de gas ideal, debes entender que la ecuación PV = nRT se puede derivar de los principios de la teoría molecular cinética, como se indicó anteriormente.
• Explicar el concepto de la vía libre media de una molécula de gas (pero sin necesidad de reproducir las matemáticas).

En esta sección, analizamos con más detalle algunos aspectos del modelo cinético-molecular y cómo se relaciona con nuestro conocimiento empírico de los gases. Para la mayoría de los estudiantes, esta será la primera aplicación del álgebra para el desarrollo de un modelo químico; esto debería ser educativo en sí mismo, ¡y puede ayudar a que ese tema vuelva a la vida para usted! Como antes, su énfasis debe en comprender estos modelos y las ideas detrás de ellos, no hay necesidad de memorizar ninguna de las fórmulas.

Imagen: Wikimedia Commons

Las V elocidades de G como M de las oleculas

A temperaturas superiores al cero absoluto, todas las moléculas están en movimiento. En el caso de un gas, este movimiento consiste en saltos en línea recta cuyas longitudes son bastante grandes en comparación con las dimensiones de la molécula. Aunque nunca podemos predecir la velocidad de una molécula individual en particular, el hecho de que usualmente estemos lidiando con un gran número de ellas nos permite saber qué fracción de las moléculas tienen energías cinéticas (y por lo tanto velocidades) que se encuentran dentro de cualquier rango dado.

La trayectoria de una molécula de gas individual consiste en una serie de trayectorias en línea recta interrumpidas por colisiones. Lo que sucede cuando dos moléculas chocan depende de sus energías cinéticas relativas; en general, una molécula más rápida o más pesada impartirá parte de su energía cinética a una más lenta o más ligera. Dos moléculas que tienen masas idénticas y que se mueven en direcciones opuestas a la misma velocidad permanecerán momentáneamente inmóviles después de su colisión.

Si pudiéramos medir las velocidades instantáneas de todas las moléculas en una muestra de un gas a alguna temperatura fija, obtendríamos un amplio rango de valores. Unos pocos serían cero, y unos pocos serían velocidades muy altas, pero la mayoría caerían en un rango más o menos bien definido. Podríamos tener la tentación de definir una velocidad promedio para una colección de moléculas, pero aquí tendríamos que tener cuidado: las moléculas que se mueven en direcciones opuestas tienen velocidades de signos opuestos. Debido a que las moléculas que están en un gas están en movimiento térmico aleatorio, habrá casi tantas moléculas moviéndose en una dirección como en la dirección opuesta, por lo que los vectores de velocidad de signos opuestos se cancelarían todos y la velocidad promedio saldría a cero. Como esta respuesta no es muy útil, necesitamos hacer nuestro promedio de una manera ligeramente diferente.

El tratamiento adecuado es promediar los cuadrados de las velocidades, y luego tomar la raíz cuadrada de este valor. La cantidad resultante se conoce como la raíz cuadrática media, o velocidad RMS

\[ \nu_{rms} = \sqrt{\dfrac{\sum \nu^2}{n}}\]

que denotaremos simplemente por\(\bar{v}\). La fórmula que relaciona la velocidad RMS con la temperatura y la masa molar es sorprendentemente simple, considerando la gran complejidad de los eventos que representa:

\[ \bar{v}= v_{rms} = \sqrt{\dfrac{3RT}{m}}\]

en la que\(m\) se encuentra la masa molar en kg mol ^—1, y k = R ÷6.02E23, la “constante de gas por molécula”, se conoce como la constante de Boltzmann.

Ejemplo\(\PageIndex{1}\)

¿Cuál es la velocidad promedio de una molécula de nitrógeno a 300 K?

Solución

La masa molar de N ₂ es de 28.01 g. Sustituyendo en la ecuación anterior y expresando R en unidades de energía, obtenemos

\[v^{2}=\frac{3 \times 8.31 \mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1} \times 300 \mathrm{K}}{28.01 \times 10^{-3} \mathrm{kg} \mathrm{mol}^{-1}}=2.67 \times 10^{5} \mathrm{J} \mathrm{kg}^{-1} \nonumber\]

Recordando la definición del joule (1 J = 1 kg m ² s ^—2) y tomando la raíz cuadrada,

\[\overline{v}=\sqrt{2.67 \times 10^{5} \mathrm{J} \mathrm{kg}^{-1} \times \frac{1 \mathrm{kg} \mathrm{m}^{2} \mathrm{s}^{-2}}{1 \mathrm{J}}}=517 \mathrm{ms}^{-1} \nonumber\]

o

\[517 \mathrm{m} \mathrm{s}^{-1} \times \frac{1 \mathrm{km}}{10^{3} \mathrm{m}} \times \frac{3600 \mathrm{s}}{1 \mathrm{h}}=1860 \mathrm{km} \mathrm{h}^{-1} \nonumber\]

Comentario: ¡esto es rápido! La velocidad de una bala de rifle suele ser de 300-500 m s ^—1; conviértalo a unidades comunes para ver la comparación por ti mismo.

Una fórmula más simple para estimar las velocidades moleculares promedio es

\[v=157 \sqrt{\dfrac{T}{m}}\]

en el que\(v\) está en unidades de metros/seg,\(T\) es la temperatura absoluta y\(m\) la masa molar en gramos.

La distribución de Boltzmann

Si tuviéramos que trazar el número de moléculas cuyas velocidades caen dentro de una serie de rangos estrechos, obtendríamos una curva ligeramente asimétrica conocida como distribución de velocidad. El pico de esta curva correspondería a la velocidad más probable. Esta curva de distribución de velocidad se conoce como la distribución de Maxwell-Boltzmann, pero con frecuencia es referida solo por el nombre de Boltzmann. La ley de distribución Maxwell-Boltzmann fue elaborada por primera vez alrededor de 1850 por el gran físico escocés, James Clerk Maxwell (izquierda, 1831-1879), quien es mejor conocido por descubrir las leyes de la radiación electromagnética. Posteriormente, el físico austriaco Ludwig Boltzmann (1844-1906) puso la relación sobre una base teórica más sólida y simplificó un poco las matemáticas. Boltzmann fue pionero en la aplicación de la estadística a la física y termodinámica de la materia, y fue un ferviente partidario de la teoría atómica de la materia en un momento en que todavía no era aceptada por muchos de sus contemporáneos.

La derivación de la curva de Boltzmann es un poco complicada para entrar aquí, pero su base física es fácil de entender. Considera una gran población de moléculas que tienen alguna cantidad fija de energía cinética. Mientras la temperatura permanezca constante, esta energía total permanecerá sin cambios, pero se puede distribuir entre las moléculas de muchas maneras diferentes, y esta distribución cambiará continuamente a medida que las moléculas choquen entre sí y con las paredes del contenedor.

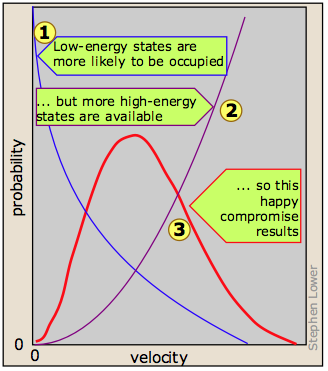
Resulta, sin embargo, que la energía cinética se adquiere y se entrega solo en cantidades discretas que se conocen como cuantos. Una vez que la molécula tiene un número dado de cuantos de energía cinética, estos pueden distribuirse entre las tres direcciones de movimiento de muchas maneras diferentes, cada una de las cuales resulta en un estado de velocidad total distinto para la molécula. Cuanto mayor sea el número de cuantos, (es decir, cuanto mayor sea la energía cinética total de la molécula) mayor será el número de estados de velocidad posibles. Si asumimos que todos los estados de velocidad son igualmente probables, entonces las estadísticas simples predicen que velocidades más altas serán más favorecidas simplemente porque hay muchos más de ellos.

Si bien el número de posibles estados de mayor energía es mayor, es más probable que los estados de menor energía estén ocupados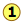. Esto se debe a que sólo tanta energía cinética disponible para el gas en su conjunto; cada molécula que adquiere energía cinética en una colisión deja atrás otra molécula que tiene menos. Esto tiende a igualar las energías cinéticas en una colección de moléculas, y asegura que siempre haya algunas moléculas cuya velocidad instantánea es cercana a cero. El efecto neto de estas dos tendencias opuestas, una que favorece las energías cinéticas altas y la otra que favorece las bajas, es la curva de pico vista arriba. Observe que debido a la asimetría de esta curva, la velocidad media (promedio rms) no es la misma que la velocidad más probable, la cual se define por el pico de la curva.

A temperaturas más altas (o con moléculas más ligeras) esta última restricción se vuelve menos importante, y la velocidad media aumenta. Pero con una distribución de velocidad más amplia, el número de moléculas que tienen una velocidad cualquiera disminuye, por lo que la curva tiende a aplanarse.

Las distribuciones de velocidad dependen de la temperatura y la masa

Las temperaturas más altas permiten que una mayor fracción de moléculas adquieran mayores cantidades de energía cinética, lo que provoca que las parcelas de Boltzmann se extiendan.

Observe cómo los extremos izquierdos de las parcelas están anclados a velocidad cero (siempre habrá algunas moléculas que pasan a estar en reposo). Como consecuencia, las curvas se aplanan a medida que las temperaturas más altas hacen que los estados de movimiento adicionales de mayor velocidad sean más accesibles. El área debajo de cada parcela es la misma para un número constante de moléculas.

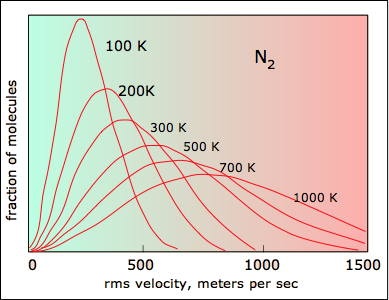
Todas las moléculas tienen la misma energía cinética (mv ² /2) a la misma temperatura, por lo que la fracción de moléculas con mayores velocidades aumentará a medida que m, y así el peso molecular, disminuya.

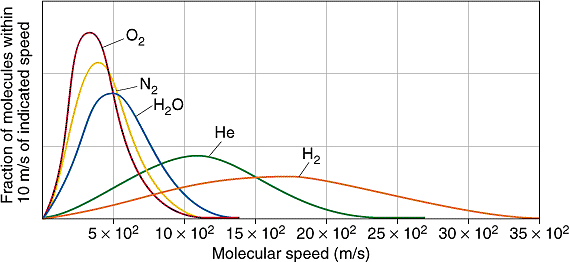
Distribución de Boltzmann y atmósferas planetarias

La capacidad de un planeta para retener un gas atmosférico depende de la velocidad promedio (y por lo tanto de la temperatura y masa) de las moléculas de gas y de la masa del planeta, lo que determina su gravedad y, por lo tanto, la velocidad de escape. Para retener un gas para la edad del sistema solar, la velocidad promedio de las moléculas de gas no debe exceder aproximadamente una sexta parte de la velocidad de escape. La velocidad de escape de la Tierra es de 11.2 km/s, y 1/6 de ésta es de aproximadamente 2 km/s El examen de la trama anterior revela que las moléculas de hidrógeno pueden alcanzar fácilmente esta velocidad, y esta es la razón por la que el hidrógeno, el elemento más abundante en el universo, está casi ausente de la atmósfera terrestre.

Aunque el hidrógeno no es un componente atmosférico significativo, el vapor de agua sí lo es. Una cantidad muy pequeña de esta se difunde hacia la parte superior de la atmósfera, donde la intensa radiación solar descompone el H ₂ O en H ₂. El escape de este hidrógeno de la atmósfera superior asciende a aproximadamente 2.5 × 10 ¹⁰ g/año.

Derivación de la ecuación de gas ideal

La ecuación de estado de gas ideal surgió combinando las leyes empíricamente determinadas (“ABC”) de Avogadro, Boyle y Charles, pero uno de los triunfos de la teoría molecular cinética fue la derivación de esta ecuación de la mecánica simple a finales del siglo XIX siglo. Este es un hermoso ejemplo de cómo los principios de la mecánica elemental pueden aplicarse a un modelo sencillo para desarrollar una descripción útil del comportamiento de la materia macroscópica. Comenzamos recordando que la presión de un gas surge de la fuerza ejercida cuando las moléculas chocan con las paredes del contenedor. Esta fuerza se puede encontrar a partir de la ley de Newton

\[f = ma = m\dfrac{dv}{dt} \label{2.1}\]

en el que\(v\) se encuentra el componente de velocidad de la molécula en la dirección perpendicular a la pared y\(m\) es su masa.

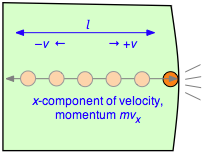
Para evaluar la derivada en la Ecuación\ ref {2.1}, que es el cambio de velocidad por unidad de tiempo, considere una sola molécula de un gas contenido en una caja cúbica de longitud\(l\). Por simplicidad, supongamos que la molécula se mueve a lo largo del eje x que es perpendicular a un par de paredes, de manera que continuamente rebota de un lado a otro entre el mismo par de paredes. Cuando la molécula de masa\(m\) golpea la pared a velocidad\(+v\) (y así con un impulso\(mv\)) rebotará elásticamente y terminará moviéndose en dirección opuesta con —v. El cambio total en la velocidad por colisión es así de 2 v y el cambio en el momento es\(2mv\).

La frecuencia de las colisiones

Después de la colisión la molécula debe recorrer una distancia l hasta la pared opuesta, y luego volver a cruzar esta misma distancia antes de chocar de nuevo con la pared en cuestión. Esto determina el tiempo entre colisiones sucesivas con un muro dado; el número de colisiones por segundo será\(v/2l\). La fuerza\(F\) ejercida sobre la pared es la velocidad de cambio del momento, dada por el producto del cambio de momento por colisión y la frecuencia de colisión:

\[F = \dfrac{d(mv_x}{dt} = (2mv_x) \times \left( \dfrac{v_x}{2l} \right) = \dfrac{m v_x^2}{l} \label{2-2}\]

La presión es fuerza por unidad de área, por lo que la presión\(P\) ejercida por la molécula en la pared de la sección transversal\(l^2\) se vuelve

\[ P = \dfrac{mv^2}{l^3} = \dfrac{mv^2}{V} \label{2-3}\]

en el que\(V\) se encuentra el volumen de la caja.

La presión producida por las moléculas de N

Como se señaló cerca del inicio de esta unidad, cualquier molécula dada hará aproximadamente el mismo número de movimientos en las direcciones positiva y negativa, por lo que tomar un promedio simple produciría cero. Para evitar esta vergüenza, cuadramos las velocidades antes de promediarlas, y luego tomar la raíz cuadrada del promedio. Este resultado se conoce como la velocidad media cuadrática (rms) de la raíz.

Hemos calculado la presión debida a que una sola molécula se mueve a velocidad constante en dirección perpendicular a una pared. Si ahora introducimos más moléculas, debemos interpretar\(v^2\) como un valor promedio que denotaremos por\(\bar{v^2}\). Además, dado que las moléculas se mueven aleatoriamente en todas las direcciones, solo un tercio de su velocidad total se dirigirá a lo largo de cualquier eje cartesiano, por lo que la presión total ejercida por\(N\) las moléculas se vuelve

\[ P=\dfrac{N}{3}\dfrac{m \bar{\nu}^2}{V} \label{2.4}\]

La afirmación anterior de que “un tercio de la velocidad total (de todas las moléculas juntas)...” no significa que 1/3 de las propias moléculas se estén moviendo en cada una de estas tres direcciones; cada partícula individual es libre de viajar en cualquier dirección posible entre colisiones. Sin embargo, cualquier trayectoria aleatoria puede considerarse compuesta por tres componentes que corresponden a estos tres ejes.

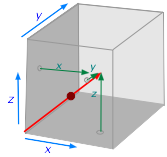
La flecha roja en la ilustración representa la trayectoria de una sola molécula a medida que viaja desde el punto de su última colisión en el origen (esquina inferior izquierda). La longitud de la flecha (que puedes reconocer como un vector) es proporcional a su velocidad. Los tres componentes de la velocidad de la molécula están indicados por las pequeñas flechas verdes. Debe ser claramente evidente que la trayectoria es principalmente a lo largo del eje x, z. En la sección que sigue, la Ecuación\ ref {2-5} contiene otro factor 1/3 que de manera similar divide la energía cinética en componentes a lo largo de los tres ejes. Esto tiene sentido porque la energía cinética está determinada en parte por la velocidad.

La temperatura de un gas es una medida de la energía cinética traslacional promedio de sus moléculas, por lo que comenzamos calculando estas últimas. Recordando que mv ² /2 es la energía cinética traslacional promedio\(ε\), podemos reescribir la Ecuación\ ref {2-4} como

\[PV = \dfrac{1}{3} N m \bar{v^2} = \dfrac{2}{3} N \epsilon \label{2-5}\]

El factor 2/3 en la proporcionalidad refleja el hecho de que los componentes de velocidad en cada una de las tres direcciones contribuyen ½ kT a la energía cinética de la partícula. La energía cinética traslacional promedio es directamente proporcional a la temperatura:

\[\epsilon = \dfrac{3}{2} kT \label{2.6}\]

en el que la constante de proporcionalidad k se conoce como la constante de Boltzmann. Sustituyendo esto en la ecuación\ ref {2-5} rendimientos

\[ PV = \left( \dfrac{2}{3}N \right) \left( \dfrac{3}{2}kT \right) =NkT \label{2.7}\]

Observe que la ecuación\ ref {2-7} se parece mucho a la ecuación de gas ideal

\[PV = nRT \nonumber \]

pero no es exactamente lo mismo, sin embargo; hemos estado usando el capital\(N\) para denotar el número de moléculas, mientras que\(n\) representa el número de moles. Y por supuesto, el factor de proporcionalidad no es la constante del gas\(R\), sino la constante de Boltzmann, 1.381 × 10 ^—23 J K ^—1. Si multiplicamos\(k\) por el número de Avogadro (\(N_A\)

\[(1.381 \times 10^{–23}{\, J \,K^{–1}) (6.022 \times 10^{23}) = 8.314 \,J \,K^{–1}.\]

De ahí que la constante de Boltzmann\(k\) sea solo la constante de gas por molécula. Así que para n moles de partículas, la Ecuación\ ref {2-7} se convierte en nuestro viejo amigo

\[ P V = n R T \label{2.8}\]

La ecuación de estado de gas ideal surgió combinando las leyes empíricamente determinadas de Boyle, Charles y Avogadro, pero uno de los triunfos de la teoría molecular cinética fue la derivación de esta ecuación de la mecánica simple a fines del siglo XIX. Este es un hermoso ejemplo de cómo los principios de la mecánica elemental pueden aplicarse a un modelo sencillo para desarrollar una descripción útil del comportamiento de la materia macroscópica, y valdrá la pena su esfuerzo por seguir y comprender los pasos individuales de la derivación. (¡Pero no te molestes en memorizarlo!)

RT tiene las dimensiones de la energía

Dado que el producto\(PV\) tiene las dimensiones de energía, también lo hace RT, y esta cantidad de hecho representa la energía cinética traduccional promedio por mol de partículas moleculares. La relación entre estas dos unidades de energía se puede obtener recordando que 1 atm es\(1.013\times 10^{5}\, N\, m^{–2}\), de manera que

\[1\, liter-atm = 1000 \mathrm{cm}^{3}\left(\frac{1 \mathrm{m}^{3}}{10^{6} \mathrm{cm}^{3}}\right) \times 1.01325 \times 10^5} \mathrm{Nm}^{2}=101325 \mathrm{J}\]

La constante gaseosa\(R\) es una de las constantes fundamentales más importantes relacionadas con el comportamiento macroscópico de la materia. Se expresa comúnmente tanto en presión-volumen como en unidades de energía:

R = 0.082057 L atm mol ^—1 K ^—1 = 8.314 J mol ^—1 K ^—1

Es decir, R expresa la cantidad de energía por grado Kelvin. Como se señaló anteriormente, la constante de Boltzmann k, que aparece en muchas expresiones relacionadas con el tratamiento estadístico de las moléculas, es justa

R ÷ 6.02E23 = 1.3807 × 10 ^—23 J K ^—1,

la “constante de gas por molécula”

¿Qué tan lejos viaja una molécula entre colisiones?

Las velocidades moleculares tienden a ser muy altas para nuestros estándares cotidianos (típicamente alrededor de 500 metros por segundo), pero incluso en los gases, chocan entre sí con tanta frecuencia que sus caminos se desvía continuamente de manera aleatoria, de modo que el movimiento neto (difusión) de una molécula a partir de una ubicación a otro ocurre con bastante lentitud. ¿Qué tan cerca pueden llegar dos moléculas?

¿Qué tan cerca pueden llegar dos moléculas? Cada molécula está rodeada por una esfera imaginaria (círculo gris) cuyo radio\(σ\) es igual a la suma de los radios de las moléculas colisionantes. Esta esfera define el volumen excluido, dentro del cual no puede entrar el centro de otra molécula.

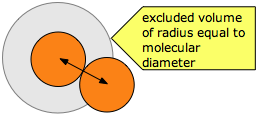
La distancia promedio que una molécula se mueve entre tales colisiones se denomina ruta libre media (\(\lambda\)), que depende del número de moléculas por unidad de volumen y de su tamaño. Para evitar colisiones, una molécula de diámetro σ debe trazar una trayectoria correspondiente al eje de un cilindro imaginario cuya sección transversal es\(\pi \sigma^2\). Eventualmente se encontrará con otra molécula (extrema derecha en el diagrama de abajo) que se ha metido en este cilindro y define el término de su libre movimiento.

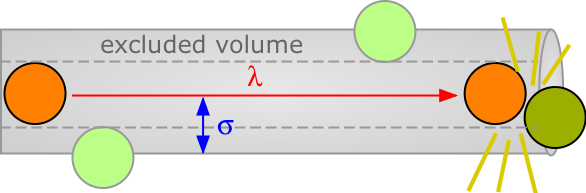
El volumen del cilindro es\(\pi \sigma^2 \lambda.\) En cada colisión la molécula se desvía a una nueva trayectoria y traza un nuevo cilindro de exclusión. Después de chocar con todas las n moléculas en un centímetro cúbico del gas habrá rastreado un volumen de exclusión total de\(\pi \sigma^2 \lambda\). Resolviendo\(\lambda\) y aplicando un factor de corrección\(\sqrt{2}\) para tener en cuenta el intercambio de impulso entre las moléculas colisionantes (el argumento detallado para esto es demasiado complicado para entrar aquí), obtenemos

\[\lambda = \dfrac{1}{\sqrt{2\pi n \sigma^2}} \label{3.1}\]

Las moléculas pequeñas como He, H ₂ y CH ₄ suelen tener diámetros de alrededor de 30-50 pm. En STP el valor de\(n\), el número de moléculas por metro cúbico, es

\[\dfrac{6.022 \times 10^{23}\; mol^{-1}}{22.4 \times 10^{-3} m^3 \; mol^{-1}} = 2.69 \times 10 \; m^{-3}\]

La sustitución en Ecuación\(\ref{3.1}\) produce un valor de alrededor\(10^{^–7}\; m (100\; nm)\) para la ruta libre media de la mayoría de las moléculas bajo estas condiciones. Aunque esto puede parecer una distancia muy pequeña, normalmente asciende a 100 diámetros moleculares y, lo que es más importante, aproximadamente 30 veces la distancia promedio entre moléculas. Esto explica por qué tantos gases se ajustan muy de cerca a la ley de gas ideal a temperaturas y presiones ordinarias.

Por otro lado, en cada colisión se puede esperar que la molécula cambie de dirección. Debido a que estos cambios son aleatorios, el cambio neto en la ubicación que experimenta una molécula durante un período de un segundo suele ser bastante pequeño. Así, a pesar de las altas velocidades moleculares, la velocidad de difusión molecular en un gas suele ser bastante pequeña.