15.5: Termodinámica de Mezcla y Dilución
- Page ID
- 71072
La energía libre de un líquido o sólido puro a 1 atm de presión es solo su energía molar libre de formación Δ G multiplicada por el número de moles presentes. Para los gases y sustancias en solución, hay que tomar en cuenta la concentración (que, en el caso de los gases, normalmente se expresa en términos de la presión). Sabemos que cuanto menor es la concentración, mayor es la entropía y, por lo tanto, menor es la energía libre. El siguiente extracto de esta lección sirve como punto de partida para el resto de la lección actual.
La entropía depende de la concentración
A medida que una sustancia se dispersa más en el espacio, la energía térmica que transporta también se extiende sobre un volumen mayor, lo que lleva a un aumento de su entropía. Debido a que la entropía, como la energía, es una propiedad extensa, una solución diluida de una sustancia dada bien puede poseer una entropía menor que el mismo volumen de una solución más concentrada, pero la entropía por mol de soluto (la entropía molar) por supuesto siempre aumentará a medida que la solución se vuelve más diluida.
Para las sustancias gaseosas, el volumen y la presión son respectivamente medidas directas e inversas de concentración. Para un gas ideal que se expande a una temperatura constante (es decir, que absorbe calor del entorno para compensar el trabajo que realiza durante la expansión), el aumento de la entropía viene dado por
\[\Delta S = R\ln \left( \dfrac{V_2}{V_1} \right) \label{2-4}\]
(Si se permite que el gas se enfríe durante la expansión, la relación se vuelve más complicada y se discutirá mejor en un curso más avanzado).
Debido a que la presión de un gas es inversamente proporcional a su volumen, podemos alterar fácilmente la relación anterior para expresar el cambio de entropía asociado con un cambio en la presión de un gas perfecto:
\[\Delta S = R\ln \left( \dfrac{P_1}{P_2} \right) \label{2-5}\]
Expresando el cambio de entropía directamente en concentraciones\(c\), tenemos la relación similar
\[\Delta S = R\ln \left( \dfrac{C_1}{C_2} \right) \label{2-6}\]
Aunque estas ecuaciones se aplican estrictamente solo a gases perfectos y no pueden usarse en absoluto para líquidos y sólidos, resulta que en una solución diluida, el soluto a menudo puede tratarse como un gas disperso en el volumen de la solución, por lo que la última ecuación puede dar un valor bastante preciso para la entropía de dilución de una solución. Veremos más adelante que esto tiene importantes consecuencias en la determinación de las concentraciones de equilibrio en una mezcla de reacción homogénea.
La energía Gibbs de un Gas: estados estándar
La presión de un gas perfecto no afecta su entalpía, pero sí afecta la entropía (cuadro a la izquierda), y así, a través del término —T Δ S, la energía libre. Cuando la presión de tal gas cambia de\(P_1\) a\(P_2\), el cambio de energía de Gibbs es
\[ \Delta G = \Delta H - T \Delta S = 0 - RT \ln \left( \dfrac{P_1}{P_2} \right) \label{4.8}\]
¿Cómo podemos evaluar la energía libre de una muestra específica de un gas a alguna presión arbitraria? Primero, recordemos que la energía molar libre estándar G° que buscarías en una tabla se refiere a una presión de 1 atm. La energía libre por mol de nuestra muestra es solo la suma de este valor y cualquier cambio en la energía libre que ocurriría si la presión se cambiara de 1 atm a la presión de interés
\[ G = G^o + RT \ln \left( \dfrac{P_1}{1\; atm} \right) \label{4.9}\]
que normalmente escribimos en forma abreviada
\[G = G^o + RT \ln P \label{4-10}\]
El término tendencia a escapar no se usa comúnmente en la termodinámica tradicional porque es esencialmente sinónimo de la energía libre, pero vale la pena conocerlo porque nos ayuda a apreciar el significado físico de la energía libre en ciertos contextos. Cuanto mayor sea la presión de un gas, mayor será la tendencia de sus moléculas a abandonar los confines del contenedor; llamaremos a esto la tendencia de escape. La ecuación anterior nos dice que la presión de un gas es una medida directamente observable de su energía libre (¡G, no G°!). Combinando estas dos ideas, podemos decir que la energía libre de un gas es también una medida de su tendencia a escapar.
De los Gases a las Soluciones: Mezcla y Dilución
Todas las sustancias, dada la oportunidad de formar una mezcla homogénea con otras sustancias, tenderán a diluirse más. Esto se puede racionalizar simplemente a partir de estadísticas elementales; hay formas más igualmente probables de disponer cien canicas negras y cien canicas blancas, que doscientas canicas de un solo color. Para objetos masivos como canicas esto no tiene nada que ver con la entropía, claro. Sin embargo, cuando se trata de un gran número de moléculas capaces de almacenar, intercambiar y difundir energía térmica, la mezcla y la expansión son definitivamente procesos impulsados por la entropía.
Se puede argumentar, de hecho, que la mezcla y la expansión son realmente muy similares; después de todo, cuando mezclamos dos gases, cada uno se está expandiendo hacia el espacio antiguamente ocupado exclusivamente por el otro.
Supongamos, por ejemplo, que tenemos un gas inicialmente confinado a la mitad de una caja, y luego retiramos la barrera para que pueda expandirse en todo el volumen del contenedor. Sabemos que la entropía del gas aumentará a medida que la energía térmica de sus moléculas se propague al espacio agrandado; el incremento real, según Ecuaciones\(\ref{2-4}\) y\(\ref{2-5}\) superiores, lo es\(R \ln 2\). Y a partir de Ecuación\(\ref{4-10}\), el cambio en\(G\) será\(–RT \ln 2\).

Ahora repitamos el experimento, pero comenzando esta vez con moléculas “rojas” en la mitad del contenedor y las “azules” en la mitad derecha. Debido a que ahora tenemos dos gases expandiéndose al doble de sus volúmenes iniciales, los cambios en S y G serán el doble de grandes:
\[ΔS = 2 R \ln 2\]
\[ΔG = –2 RT \ln 2\]
Sin embargo, observe que aunque cada gas sufrió una expansión, el proceso global en este caso es equivalente a la mezcla.
Lo que es cierto para las moléculas gaseosas puede, en principio, aplicarse también a las moléculas de soluto disueltas en un disolvente. Una calificación importante aquí es que la solución debe ser ideal, es decir, que la fuerza de las interacciones entre todo tipo de moléculas (solutos A y B, y el disolvente) debe ser la misma. Recuerde que la entalpía asociada a la expansión de un gas perfecto es por definición cero. Por el contrario, los\(ΔH_{mixing}\) de dos líquidos o de disolver un soluto en un disolvente tienen valores finitos que pueden limitar la miscibilidad de los líquidos o la solubilidad de un soluto.
Dada esta condición, podemos definir la energía de Gibbs de dilución o mezcla sustituyendo esta ecuación en la definición de Δ G:
\[ \Delta G_{dilution} = \Delta H_{dilution} - RT\ln \left( \dfrac{C_1}{C_2} \right) \label{4-11}\]
Si la sustancia en cuestión forma una solución ideal con los demás componentes, entonces\(ΔH_{diution}\) es cero, y podemos escribir
\[ \Delta G_{dilution} = RT\ln \left( \dfrac{C_2}{C_1} \right) \label{4-12}\]
Estas relaciones nos dicen que la dilución de una sustancia desde una concentración inicial\(C_1\) hasta una concentración más diluida\(C_2\) va acompañada de una disminución en la energía libre, y así ocurrirá espontáneamente. De la misma manera, no se producirá la “desdilución” espontánea de una solución (¡no esperamos que el té vuelva a difundirse en la bolsa de té!) Sin embargo, la no dilución puede verse obligada a ocurrir si se pueden encontrar algunos medios para suministrar al sistema una cantidad de energía (en forma de trabajo) igual a\(\Delta G_{dilution} \).
Un ejemplo práctico importante de ello es el trabajo metabólico que realizan los riñones en la concentración de sustancias de la sangre para su excreción en la orina.
Para encontrar la energía Gibbs de un soluto a alguna concentración arbitraria, procedemos de la misma manera que lo hicimos para un gas: tomamos la suma de la energía libre estándar más cualquier cambio en la energía libre que acompañaría a un cambio en la concentración del estado estándar al estado real de la solución. De la ecuación\(\ref{4-12}\) es fácil derivar una expresión análoga a la ecuación\(\ref{4-10}\):
\[G = G^o + RT \ln C \label{4-13}\]
que da la energía libre de un soluto a alguna concentración arbitraria\(C\) en términos de su valor\(G^o\) en su estado estándar.
Si bien Ecuación\(\ref{4-13}\) tiene la misma forma simple que Ecuación\(\ref{4-10}\), su aplicación práctica está plagada de dificultades, siendo la principal que no suele dar valores\(G\) que sean consistentes con el experimento, especialmente para solutos que son iónicos o son ligeramente solubles. Esto se debe a que la mayoría de las soluciones (especialmente las que contienen iones disueltos) están lejos de ser ideales; las interacciones intermoleculares entre moléculas de soluto y entre soluto y disolvente devuelven el término de entalpía que dejamos fuera al derivar la Ecuación\(\ref{4-12}\). Además, la organización estructural de la solución se vuelve dependiente de la concentración, por lo que la entropía depende de la concentración de una manera más complicada de lo que implica el análogo de concentración de la Ecuación\(\ref{4-12}\).
Reacciones Químicas y Mezcla
Caracterizamos la tendencia de una reacción química A → B a ocurrir a temperatura y presión constantes por el valor de su cambio energético estándar de Gibbs Δ G°. Si esta cantidad es negativa, sabemos que la reacción se llevará a cabo de manera espontánea. No obstante, ¿alguna vez te has preguntado por qué es que la sustancia A no se transforma completamente en B si esta última es termodinámicamente más estable? La respuesta es que si la reacción tiene lugar en una sola fase (gas o líquido), algo más está sucediendo: A y B se están mezclando, y este proceso crea su propio cambio de energía Gibbs\(ΔG_{mixing}\). Para una mezcla binaria simple de A y B (sin ninguna reacción), los cambios en\(S\) y\(G\) pueden ser representados por estas gráficas simples:
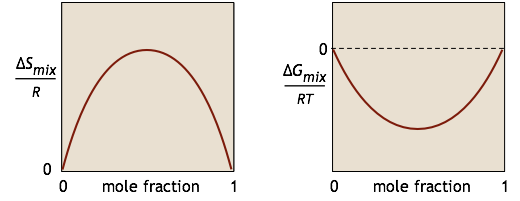
No vamos a tratar de probarlo aquí, pero resulta que por más baja que sea la energía Gibbs de los productos en comparación con la de los reactivos, la energía libre del sistema siempre se puede reducir aún más si algunos de los reactivos permanecen en la solución para aportar una mezcla Δ G término. Esta es la razón por la que una gráfica de G en función de la composición de dicho sistema tiene un mínimo en algún momento corto de conversión completa.

D iffusion se refiere al transporte de una sustancia a través de un gradiente de concentración. La dirección es siempre hacia la región de menor concentración. Ahora se debe ver que desde un punto de vista termodinámico, estos procesos son idénticos en que ambos representan el “escape” espontáneo de moléculas de una región de mayor concentración (menor entropía, mayor energía de Gibbs) a una región de menor concentración.
En lugar de complicar G° tratando de corregir todos estos efectos, los químicos han optado por conservar su forma simple haciendo un solo pequeño cambio en la forma de\(\ref{4-13}\):
\[G = G^o + RT \ln a \label{4-14}\]
Esta ecuación está garantizada para funcionar, porque a, la actividad del soluto, es su concentración termodinámicamente efectiva. La relación entre la actividad y la concentración viene dada por
\[a = \gamma c \label{4-15}\]
donde\(\gamma\) está el coeficiente de actividad. A medida que la solución se diluye, el coeficiente de actividad se acerca a la unidad:
\[ \lim _{c \rightarrow 0} \gamma =1 \label{4.16}\]
El precio que pagamos por esta simplicidad es que la relación entre la concentración y la actividad a concentraciones más altas puede ser bastante complicada, y debe determinarse experimentalmente para cada solución diferente.
La pregunta de qué estado estándar elegimos para el soluto (es decir, ¿a qué concentración se define G°, y en qué unidades se expresa?) es uno que desearás que nunca hubieras preguntado. Podríamos tener la tentación de usar una concentración de 1 molar, pero una solución tan concentrada estaría sujeta a todo tipo de efectos de interacción intermolecular, y no haría un estado estándar muy práctico. Estos efectos podrían eliminarse yendo al extremo opuesto de una solución “infinitamente diluida”, pero por Ecuación\(\ref{4-12}\) esto implicaría una energía libre de menos infinito para el soluto, lo que sería incómodo. Por lo tanto, los químicos han acordado definir el estado estándar de un soluto como uno en el que la concentración es de 1 molar, pero todas las interacciones soluto-soluto están mágicamente apagadas, de manera que eso\(\gamma\) es efectivamente la unidad. Como esto es imposible, en realidad no puede existir ninguna solución correspondiente a este estado estándar, pero esto resulta ser solo un pequeño inconveniente, y parece ser el mejor compromiso entre conveniencia, utilidad y realidad.


