21.4: Teoría de Bohr del Átomo
- Page ID
- 75243
En un artículo clásico publicado en 1913, el joven Niels Bohr, entonces trabajando con Rutherford en Manchester, Inglaterra, procedió a mostrar cómo la fórmula de Rydberg podría explicarse en términos de un modelo muy simple del átomo de hidrógeno. El modelo se basaba en la visión nuclear de la estructura atómica que acababa de ser propuesta por Rutherford. El modelo de Bohr se muestra en la Figura\(\PageIndex{1}\). Un electrón de carga — e y masa\(m\) se mueve alrededor de un núcleo pesado de carga + e. Ordinariamente el electrón se movería en línea recta, pero la atracción del núcleo dobla su trayectoria para que se mueva con una velocidad constante\(u\) en un círculo perfecto de radio r alrededor del núcleo. La situación y las matemáticas son muy similares a la de un planeta ardiendo alrededor del sol. La principal diferencia es que en lugar de la fuerza de gravedad existe una fuerza electrostática de atracción\(F\) entre el protón y el electrón descrita por la ley de Coulomb:
\[F=k\frac{e^{2}}{r^{2}} \label{1} \]
donde\(k\) tiene el valor 8.9876 × 10 9 J m C —2.
Las expresiones tanto para las energías cinéticas como potenciales del electrón se pueden derivar usando la ecuación\(\ref{1}\) y los principios de la física elemental. Tal derivación se puede encontrar en la mayoría de los textos introductorios de física. Las dos expresiones son
\[E_{k}=\frac{1}{2}mu^{2}=\frac{1}{2}k\frac{e^{2}}{r} \label{2} \]
y
\[E_{p}=-k\frac{e^{2}}{r} \label{3} \]
Si estos se suman, obtenemos una fórmula simple para la energía total del electrón:
\[\begin{align} E &=E_{k}+E_{p} \\[4pt] &=-\frac{1}{2}k\frac{e^{2}}{r} \label{4} \end{align} \]
Si ahora insertamos los valores conocidos de\(e\) y\(k\), tenemos el resultado
\[ \begin{align} E &= -\frac{1}{2}\times\frac{8.9876 \times 10^{9} \text{ J m C}^{-2}\times(1.6022 \times 10^{-19} \text{ C})^{2}}{r} \\[4pt] &=-\frac{1.1536 \times 10^{-28} \text{ J M} }{r} \label{5} \end{align} \]
De la Ecuación\(\ref{5}\) vemos que la energía total del electrón es muy negativa para una órbita con un radio pequeño pero aumenta a medida que la órbita se hace más grande.
Además de sugerir el modelo planetario que acabamos de describir, Bohr también hizo otros dos postulados que le permitieron explicar el espectro del hidrógeno. El primero de ellos fue la sugerencia de que un electrón de alta energía que circunda el núcleo en un radio grande puede perder parte de esa energía y asumir una órbita de menor energía más cercana al núcleo. La energía perdida por el electrón es emitida como un fotón de luz de frecuencia\(\nu\) dada por la fórmula de Planck
\[\Delta E = h\upsilon \label{6} \]
donde\(ΔE\) esta la energía perdida por el electrón.
El segundo postulado de Bohr fue que sólo ciertas órbitas son posibles al electrón en un átomo de hidrógeno. Esto le permitió explicar por qué es que sólo la luz de unas pocas frecuencias particulares puede ser emitida por el átomo de hidrógeno. Dado que sólo se permite un número limitado de órbitas, cuando un electrón se desplaza de una órbita externa a una interna, el fotón que emerge no puede tener cualquier frecuencia sino sólo esa frecuencia correspondiente a la diferencia de energía entre dos órbitas permitidas.
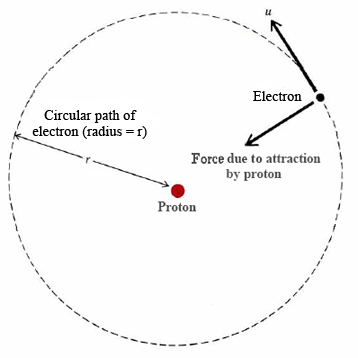
Según la teoría de Bohr, dos de las órbitas permitidas en el átomo de hidrógeno tienen radios de 52.918 y 211.67 pm. Calcular la energía, la frecuencia y la longitud de onda del fotón emitido cuando el electrón se mueve del exterior al interior de estas dos órbitas.
Solución
Al etiquetar la órbita externa 2 y la órbita interna 1, primero calculamos la energía de cada órbita a partir de la ecuación\(\ref{5}\):
\[E_{2}=-\dfrac{1.1536\times10^{-28} \text{Jm}}{211.67\times10^{-12} \text{m}}=-0.54500 \text{aJ} \nonumber \]
\[E_{1}=-\dfrac{1.1536\times10^{-28} \text{Jm}}{52.918\times10^{-12} \text{m}}=-2.1780\, \text{aJ} \nonumber \]
Así
\[ \Delta E = – 0.545 00 \text{aJ} – (– 2.1780 \text{aJ}) = 1.6330\, \text{aJ} \nonumber \]
Usando Ecuación\(\ref{6}\), ahora tenemos
\[\upsilon=\dfrac{\Delta E}{h}=\dfrac{1.6330\times10^{-18}\text{ J}}{6.6262\times10^{-34} \text{ J s}}=2.4645\times10^{15} \text{ s}^{-1}=2.4645 \text{ PHz} \nonumber \]
Por último\( \lambda = \dfrac{c}{\upsilon} = 1.2164 \times 10^{-7} \text{ m} = 121.64 \text{ nm} \). Para predecir las frecuencias correctas para las líneas en el espectro de hidrógeno, Bohr encontró que tenía que asumir que la cantidad\(mur\) (llamada el momento angular por los físicos) necesitaba ser un múltiplo de\(h/2π\). En otras palabras, se encontró que la condición que restringía las órbitas a solo ciertos radios y ciertas energías era
\[mur=\frac{nh}{2\pi} \qquad \label{7} \]
donde podría tener el valor 1, 2, 3, etc.
Al manipular ambas Ecuaciones\(\ref{7}\) y\(\ref{2}\), es posible demostrar que esta restricción en el momento angular restringe los radios de las órbitas a los dados por la expresión
\[ r = \frac{n^{2}h^{2}}{4\pi^{2}mke^{2}} \qquad n = 1, 2, 3, \cdots \label{8} \]
Si se insertan los valores conocidos de h, m, k y e, esta fórmula se reduce a la forma conveniente
\[ r = n^2 \times 52.918 \text{ pm} \qquad n = 1, 2, 3, \cdots \label{9} \]
El postulado de Bohr restringe así el electrón a órbitas para las cuales el radio es de 52.9 pm, 2 2 × 52.9 pm, 3 2 × 52.9 pm, y así sucesivamente.
Si sustituimos Ecuación\(\ref{8}\) por Ecuación\(\ref{4}\), llegamos a una expresión general para la energía en términos de n:
\[E=-\frac{1}{2}k\frac{e^{2}}{r}=-\frac{1}{2}ke^{2}\times\frac{4\pi^{2}mke^{2}}{n^{2}h^{2}} =\frac{2\pi^{2}k^{2}e^{4}m}{n^{2}h^{2}} \label{10} \]Nuevamente sustituyendo en los valores conocidos por todas las constantes, obtenemos\[E=-\frac{2.1800 \text{ aJ}}{n^{2}} \label{11} \]
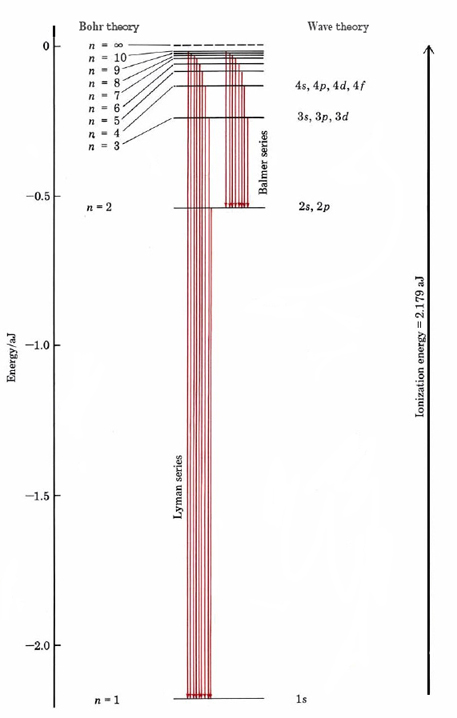
El entero determina\(n\) así qué tan lejos está el electrón del núcleo y cuánta energía tiene, así como el número cuántico principal\(n\) descrito anteriormente.
Usando Ecuación\(\ref{10}\) o\(\ref{11}\) encontrar la energía de ionización del átomo de hidrógeno.
Solución
La energía de ionización del átomo de hidrógeno corresponde a la diferencia de energía entre el electrón en su órbita más interna (n = 1) y el electrón cuando está completamente separado del protón. Para el electrón completamente separado r = ∞ (infinito) y también lo hace n. Así
\[E_{1}=-\dfrac{2.1800 \text{aJ}}{1^{2}}=-2.1800\text{aJ} \nonumber \]
y
\[E_{\infty}=-\dfrac{2.1800 \text{aJ}}{\infty^{2}}=0.0000\text{aJ} \nonumber \]
La diferencia de energía es así
\[\Delta E=E_{infty}-E_{1}=2.1800 \text{aJ} \nonumber \]
que es la energía de ionización por átomo. Sobre una base molar la energía de ionización es la constante de Avogadro multiplicada por esta cantidad; es decir,
\[2.1800 \times 10^{-18} \text{J} \times 6.0221 \times 10^{23} \text{mol}^{-1} = 1312.8 \text{ kJ mol}^{-1}\ n\nonumber \]
Nota: En un átomo, la configuración electrónica de la energía más baja se denomina estado fundamental mientras que otras configuraciones se denominan estados excitados.
Ahora podemos derivar la fórmula experimental de Rydberg a partir de la teoría de Bohr. Supongamos que un electrón se mueve desde una órbita externa para la que el número cuántico es n 2 a una órbita interna del número cuántico n 1. La energía perdida por el electrón y emitida como fotón es dada entonces por
\[\Delta E=E_{2}-E_{1}= – 2.1800 \text{ aJ} \left(\frac{1}{n_{2}^{2}}-\frac{1}{n_{1}^{2}}\right) = 2.1800 \text{ aJ} \left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right) \label{12} \]
Sin embargo,
\[\Delta E=h\upsilon=\frac{hc}{\lambda} \label{13} \]
donde\(λ\) está la longitud de onda del fotón. Combinando Eqs. \(\ref{2}\)y\(\ref{3}\), obtenemos
\[\frac{1}{\lambda}=\frac{2.1800 \text{ aJ}}{hc}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right) \nonumber \]
o
\[\frac{1}{\lambda}=1.0975\times10^{7}m^{-1} \left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right) \label{14} \]
Esta expresión es exactamente de la misma forma que la encontrada experimentalmente por Rydberg con un valor para R ∞ de 1.0974 × 10 7 m —1, muy cercano al valor experimental de 1.097 094 × 10 7 m —1. Aún mejor acuerdo se puede obtener si se tiene en cuenta que el núcleo no es estacionario sino que el electrón y el núcleo giran alrededor de un centro de gravedad común.
Calcular la longitud de onda de la luz emitida cuando el electrón en un átomo de hidrógeno cae de la órbita n = 3 a la n = 1. ¿En qué región del espectro se encuentra esta línea espectral? ¿A qué serie pertenece?
Solución
De Ecuación\(\ref{14}\) encontramos
\[\dfrac{1}{\lambda}=1.0975\times10^{7}m^{-1}\times\left(1-\dfrac{1}{9}\right)=9.7547\times10^{6}m^{-1} \nonumber \]
dando\(\lambda = 102.51 \text{ nm} \). Esta es la segunda línea de la serie Lyman y se encuentra en el lejano ultravioleta. La longitud de onda determinada experimentalmente es de 102.573 nm.
El éxito de Bohr con el átomo de hidrógeno pronto llevó a intentos tanto de él como de otros de extender el mismo modelo a otros átomos. A nivel cualitativo estos intentos tuvieron cierto éxito, y comenzó a emerger una imagen general de electrones ocupando órbitas en niveles y subniveles sucesivos, similar al que se muestra en la Figura 5.2. A nivel cuantitativo, sin embargo, todos los intentos de calcular valores precisos para las energías de los electrones en sus orbitales cuantificados fueron fallas sombrías. No fue sino hasta la introducción de la mecánica de olas por parte de Schrödinger en 1926 que estas dificultades pudieron resolverse. De pronto, al parecer, todo cayó en su lugar. Desde entonces prácticamente todas las líneas del espectro de cada elemento se han contabilizado teóricamente. Como resultado, ahora tenemos una imagen muy exacta, aunque matemáticamente bastante compleja, del comportamiento de los electrones tanto en el estado fundamental como en los estados excitados de los átomos. En particular, el estudio de los espectros atómicos nos ha permitido determinar con mucha precisión las energías de ionización de todos los elementos.
Los detalles de los espectros de los átomos polielectrónicos son complejos, por lo que consideraremos sólo un ejemplo: el sodio. Los estados excitados de sodio pueden obtenerse incrementando la energía del átomo para que el electrón de valencia de 3 s ocupe el 3 p, 3 d, 4 s, 4 p, 4 d, 4 f o algún otro orbital. Sin embargo, en contraste con el átomo de hidrógeno, un átomo de sodio tiene otros electrones que blindan al electrón de valencia de la carga nuclear, y este blindaje es diferente para cada forma orbital diferente (s, p, d, f, etc.). En consecuencia, la energía de un átomo de sodio excitado cuya configuración electrónica es 1 s 2 2 s 2 2 p 6 4 s 1 no es la misma que la de un átomo de sodio excitado cuya configuración es 1 s 2 2 s 2 2 p 6 4 p 1. Diferente blindaje del electrón más externo (4 s o 4 p) da como resultado una energía diferente. Debido a esto, se necesitan cuatro fórmulas para describir la energía del átomo de sodio, una para cada una de las formas orbitales disponibles para el electrón más externo:
\[\begin{align*} E_{ns} & =\frac{2.1800 \text{ aJ}}{(n-a_{s})^{2}}\\E_{np} & =\frac{2.1800 \text{ aJ}}{(n-a_{p})^{2}}\\ E_{nd} &= \frac{2.1800 \text{ aJ}}{(n-a_{d})^{2}}\\ E_{nf} & = \frac{2.1800 \text{ aJ}}{(n-a_{f})^{2}} \end{align*} \nonumber \]
En todas estas ecuaciones n representa el número cuántico principal. Debe ser 3 o mayor ya que el electrón se encuentra en el orbital de 3 s para empezar. El blindaje diferente requiere una corrección diferente para cada tipo de orbital: a s = 1.36; a p = 0.87; a d = 0.012; y a f = 0.001.
Debido a que hay cuatro conjuntos diferentes de niveles de energía, el número de transiciones entre niveles (y por lo tanto el número de líneas en el espectro) es mayor para el sodio que para el hidrógeno. Los primeros espectroscopistas pudieron distinguir cuatro tipos diferentes de líneas, las cuales etiquetaron las series aguda, principal, difusa y fundamental. Es a partir de la abreviatura de estos términos que hemos obtenido los símbolos modernos s, p, d y f.
Como la mayoría de los lectores sabrán, cuando casi cualquier compuesto de sodio se mantiene en un quemador Bunsen, imparte un color amarillo brillante a la llama. Este color amarillo corresponde a la línea más prominente en el espectro del sodio. Su longitud de onda es de 589 nm. En la escala atómica esta línea es causada por el átomo de sodio que pasa de un estado excitado (en el que el electrón de valencia está en un orbital de 3 p) al estado fundamental (en el que el electrón se encuentra en un orbital de 3 s). Usando las ecuaciones anteriores podemos obtener valores aproximados para las dos energías involucradas en la transición:
\[E_{3p}=\frac{2.1800 \text{ aJ}}{(3-0.87)^{2}}=-0.4805\, \text{ aJ} \nonumber \]
y
\[E_{3s}=\dfrac{2.1800 \text{ aJ}}{(3-1.36)^{2}}=-0.8105\, \text{ aJ}. \nonumber \]
Así\(\Delta E= 0.3300 \text{ aJ}\) dando\(\lambda = \dfrac{hc}{\Delta E}=602 \text{ nm}\) Esto concuerda aproximadamente con el resultado experimental. Otra característica del espectro del sodio merece mención. La observación cuidadosa revela que el color amarillo del sodio en realidad se debe a dos líneas muy espaciadas (un doblete). Uno tiene una longitud de onda de 588.995 nm, y el otro está en 589.592 nm. Cuando el electrón está en un orbital de 3 p, su espín puede alinearse de dos maneras con respecto al eje del orbital. La pequeña diferencia de energía entre estas dos orientaciones da como resultado dos longitudes de onda ligeramente diferentes


