5.2: Calorimetría

Objetivos de aprendizaje

• Explicar la técnica de calorimetría
• Calcular e interpretar el calor y las propiedades relacionadas utilizando datos típicos de calorimetría

Una técnica que podemos usar para medir la cantidad de calor involucrada en un proceso químico o físico se conoce como calorimetría. La calorimetría se utiliza para medir las cantidades de calor transferidas hacia o desde una sustancia. Para ello, el calor se intercambia con un objeto calibrado (calorímetro). El cambio de temperatura de la parte de medición del calorímetro se convierte en la cantidad de calor (ya que se utilizó la calibración previa para establecer su capacidad calorífica). La medición de la transferencia de calor mediante este enfoque requiere la definición de un sistema (la sustancia o sustancias que sufren el cambio químico o físico) y su entorno (los demás componentes del aparato de medición que sirven para proporcionar calor al sistema o absorber el calor del sistema). El conocimiento de la capacidad calorífica del entorno, y mediciones cuidadosas de las masas del sistema y alrededores y sus temperaturas antes y después del proceso permite calcular el calor transferido como se describe en esta sección.

Un calorímetro es un dispositivo utilizado para medir la cantidad de calor involucrada en un proceso químico o físico. Por ejemplo, cuando ocurre una reacción exotérmica en solución en un calorímetro, el calor producido por la reacción es absorbido por la solución, lo que aumenta su temperatura. Cuando se produce una reacción endotérmica, el calor requerido es absorbido por la energía térmica de la solución, lo que disminuye su temperatura (Figura\(\PageIndex{1}\)). El cambio de temperatura, junto con el calor específico y la masa de la solución, se pueden usar para calcular la cantidad de calor involucrada en cualquier caso.

Figura\(\PageIndex{1}\): En una determinación calorimétrica, ya sea (a) se produce un proceso exotérmico y el calor, q, es negativo, lo que indica que la energía térmica se transfiere del sistema a su entorno, o bien (b) se produce un proceso endotérmico y el calor, q, es positivo, lo que indica que se transfiere energía térmica desde los alrededores hasta el sistema.

Se muestran dos diagramas etiquetados como a y b. Cada uno se compone de dos recipientes rectangulares con un termómetro insertado en la parte superior derecha y extendiéndose por dentro. Hay una flecha orientada hacia la derecha que conecta cada caja en cada diagrama. El contenedor izquierdo en el diagrama a representa una solución arremolinada rosa y verde con los términos “Proceso exotérmico” y “Sistema” escritos en el centro con flechas orientadas hacia afuera de los términos que apuntan a “q”. Las etiquetas “Solución” y “Alrededores” están escritas en la parte inferior del contenedor. El contenedor derecho en el diagrama a tiene el término “Solución” escrito en la parte inferior del contenedor y una flecha roja hacia arriba cerca del termómetro con la frase “Temperatura aumentada” al lado del mismo. Los remolinos rosados y verdes se mezclan más en este contenedor. El contenedor izquierdo en el diagrama b representa una solución arremolinada púrpura y azul con los términos “Proceso endotérmico” y “Sistema” escritos en el centro con flechas orientadas hacia los términos y “Solución” y “Alrededores” escritos en la parte inferior. Las flechas apuntan lejos de la letra “q”. El contenedor derecho en el diagrama b tiene el término “Solución” escrito en la parte inferior y una flecha roja hacia abajo cerca del termómetro con la frase “Temperatura disminuida” junto a él. Los remolinos azules y morados se mezclan más en este contenedor.

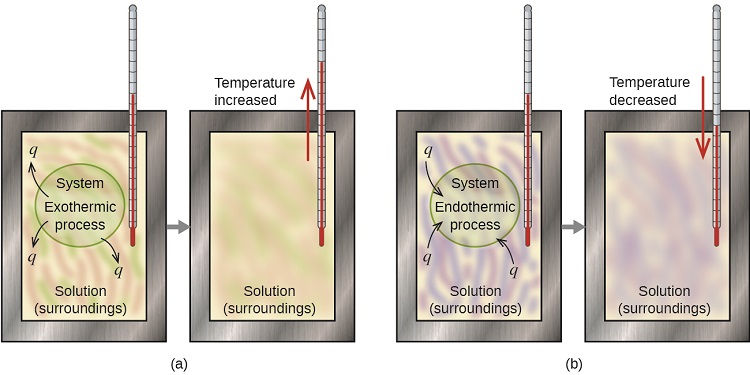
Por convención, q recibe un signo negativo (-) cuando el sistema libera calor al entorno (exotérmico); q recibe un signo positivo (+) cuando el sistema absorbe calor del entorno (endotérmico).

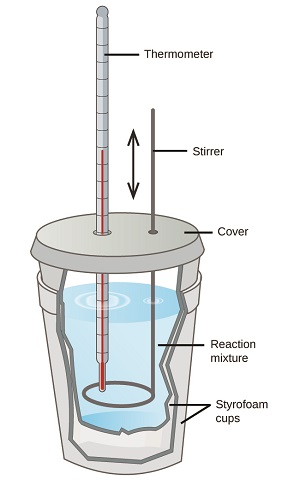
Los científicos utilizan calorímetros bien aislados que casi impiden la transferencia de calor entre el calorímetro y su entorno. Esto permite determinar con precisión el calor involucrado en los procesos químicos, el contenido energético de los alimentos, etc. Los estudiantes de química general suelen utilizar calorímetros simples construidos a partir de tazas de poliestireno (Figura\(\PageIndex{2}\)). Estos calorímetros de “taza de café” fáciles de usar permiten un mayor intercambio de calor con su entorno y, por lo tanto, producen valores de energía menos precisos.

Figura\(\PageIndex{2}\): Se puede construir un calorímetro simple a partir de dos copas de poliestireno. Un termómetro y un agitador se extienden a través de la cubierta hacia la mezcla de reacción.

Dos copas de espuma de poliestireno se muestran anidadas una en la otra con una cubierta sobre la parte superior. Un termómetro y una varilla de agitación se insertan a través de la tapa y dentro de la solución dentro de la taza, que se muestra como un corte. La varilla agitadora tiene una flecha de doble punta junto a ella orientada hacia arriba y hacia abajo. La mezcla líquida dentro de la taza está etiquetada como “Mezcla de reacción”.

También hay disponibles calorímetros de solución comercial. Los calorímetros relativamente económicos a menudo consisten en dos copas de pared delgada que están anidadas de una manera que minimiza el contacto térmico durante el uso, junto con una cubierta aislada, agitador de mano y termómetro simple. Los calorímetros más caros utilizados para la industria y la investigación suelen tener un recipiente de reacción bien aislado y completamente cerrado, un mecanismo de agitación motorizado y un sensor de temperatura más preciso (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Los calorímetros de soluciones comerciales van desde (a) modelos simples y económicos para uso estudiantil hasta (b) modelos caros y más precisos para la industria y la investigación.

Se muestran dos diagramas y se etiquetan como a y b. El diagrama a representa un termómetro que pasa a través de una cubierta aislante similar a un disco y dentro de un cilindro de metal que está etiquetado como “recipiente interior de metal”, que a su vez está anidado en un cilindro de metal etiquetado como “recipiente exterior de metal”. El cilindro interior descansa sobre un anillo de soporte aislante. Un agitador pasa a través de la cubierta aislante y también dentro del cilindro interior. El diagrama b muestra un recipiente metálico interior medio lleno de líquido que descansa sobre un anillo de soporte aislante y anidado en un recipiente exterior metálico. Una sonda de temperatura de precisión y una varilla de agitación motorizada se colocan en la solución en el recipiente interno y se conectan por cables al equipo exterior a la configuración.

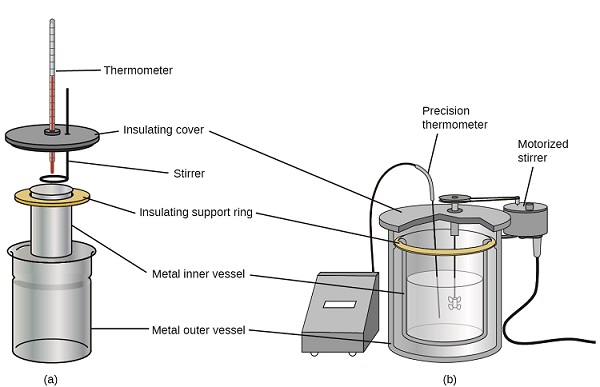
Antes de practicar problemas de calorimetría que involucran reacciones químicas, consideremos un ejemplo simple que ilustra la idea central detrás de la calorimetría. Supongamos que inicialmente tenemos una sustancia de alta temperatura, como una pieza caliente de metal (M), y una sustancia a baja temperatura, como el agua fría (W). Si colocamos el metal en el agua, el calor fluirá de M a W. La temperatura de M disminuirá, y la temperatura de W aumentará, hasta que las dos sustancias tengan la misma temperatura, es decir, cuando alcancen el equilibrio térmico (Figura\(\PageIndex{4}\)). Si esto ocurre en un calorímetro, lo ideal sería que toda esta transferencia de calor se produzca entre las dos sustancias, sin que el calorímetro o el entorno del calorímetro no se pierda calor. Bajo estas circunstancias ideales, el cambio neto de calor es cero:

\[q_\mathrm{\,substance\: M} + q_\mathrm{\,substance\: W}=0 \label{5.3.1} \]

Esta relación se puede reorganizar para mostrar que el calor ganado por la sustancia M es igual al calor perdido por la sustancia W:

\[q_\mathrm{\,substance\: M}=-q_\mathrm{\,substance\: W} \label{5.3.2} \]

La magnitud del calor (cambio) es por lo tanto la misma para ambas sustancias, y el signo negativo simplemente muestra eso\(q_{substance\, M}\) y\(q_{substance\, W}\) son opuestos en la dirección del flujo de calor (ganancia o pérdida) pero no indica el signo aritmético de ninguno de los dos valores q (es decir, determinado por si el materia en cuestión gana o pierde calor, por definición). En la situación específica descrita,\(q_{substance\, M}\) es un valor negativo y\(q_{substance\, W}\) es positivo, ya que el calor se transfiere de M a W.

Figura\(\PageIndex{4}\): En un proceso simple de calorimetría, (a) el calor, q, se transfiere del metal caliente, M, al agua fría, W, hasta que (b) ambos estén a la misma temperatura.

Se muestran dos diagramas y se etiquetan a y b. Cada diagrama está compuesto por un recipiente rectangular con un termómetro insertado en su interior desde la esquina superior derecha. Ambos contenedores están conectados por una flecha orientada hacia la derecha. Ambos contenedores están llenos de agua, que se representa con la letra “W”, y cada recipiente tiene un cuadrado en el medio que representa un metal que está etiquetado con una letra “M”. En el diagrama a, el metal se dibuja en color marrón y tiene tres flechas orientadas en sentido contrario a él. Cada flecha tiene la letra “q” en su extremo. El metal está etiquetado como “sistema” y el agua está etiquetada como “entorno”. El termómetro en este diagrama tiene una lectura relativamente baja. En el diagrama b, el metal se representa en púrpura y el termómetro tiene una lectura relativamente alta.

Ejemplo\(\PageIndex{1}\): Heat Transfer between Substances at Different Temperatures

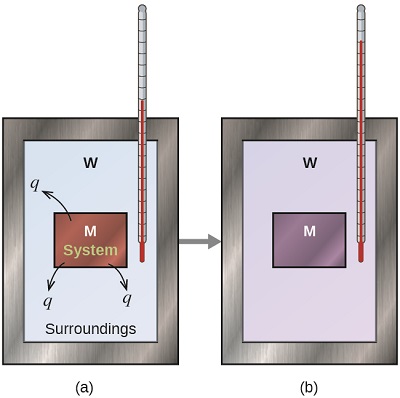
Una pieza de refuerzo caliente de 360 g (una varilla de acero utilizada para el refuerzo de concreto) se deja caer en 425 mL de agua a 24.0 °C. La temperatura final del agua se mide como 42.7 °C. Calcular la temperatura inicial de la pieza de armadura. Supongamos que el calor específico del acero es aproximadamente el mismo que el del hierro (Cuadro T4), y que toda la transferencia de calor ocurre entre la armadura y el agua (no hay intercambio de calor con los alrededores).

Solución

La temperatura del agua aumenta de 24.0 °C a 42.7 °C, por lo que el agua absorbe calor. Ese calor provenía de la pieza de armadura, que inicialmente estaba a una temperatura más alta. Suponiendo que toda la transferencia de calor estaba entre la barra de refuerzo y el agua, sin que el calor “se perdiera” a los alrededores, entonces el calor desprendido por la barra de refuerzo = − calor absorbido por el agua, o:

\[q_\ce{rebar}=−q_\ce{water} \nonumber \]

Como sabemos cómo se relaciona el calor con otras cantidades medibles, tenemos:

\[(c×m×ΔT)_\ce{rebar}=−(c×m×ΔT)_\ce{water} \nonumber \]

Dejando f = final e i = inicial, en forma expandida, esto se convierte en:

\[ c_\ce{rebar}×m_\ce{rebar}×(T_\mathrm{f,rebar}−T_\mathrm{i,rebar})=−c_\ce{water}×m_\ce{water}×(T_\mathrm{f,water}−T_\mathrm{i,water}) \nonumber \]

La densidad del agua es de 1.0 g/mL, por lo que 425 mL de agua = 425 g. Observando que la temperatura final tanto de la barra de refuerzo como del agua es de 42.7 °C, sustituyendo valores conocidos rinde:

\[ \mathrm{(0.449\:J/g\: °C)(360g)(42.7°C−\mathit T_\mathrm{i,rebar})=-(4.184\:J/g\: °C)(425\:g)(42.7°C−24.0°C)} \nonumber \]

\[\mathrm{\mathit T_{i,rebar}=\dfrac{(4.184\:J/g\: °C)(425\:g)(42.7°C−24.0°C)}{(0.449\:J/g\: °C)(360\:g)}+42.7°C} \nonumber \]

Resolver esto da Ti, rebar= 248 °C, por lo que la temperatura inicial de la barra de refuerzo fue 248 °C.

Ejercicio\(\PageIndex{1A}\)

Se deja caer una pieza de cobre de 248 g en 390 mL de agua a 22.6 °C. La temperatura final del agua se midió como 39.9 °C. Calcular la temperatura inicial de la pieza de cobre. Supongamos que toda la transferencia de calor ocurre entre el cobre y el agua.

Contestar

La temperatura inicial del cobre fue de 335.6 °C.

Ejercicio\(\PageIndex{1B}\)

Una pieza de cobre de 248 g inicialmente a 314 °C se deja caer en 390 mL de agua inicialmente a 22.6 °C. Suponiendo que toda la transferencia de calor ocurre entre el cobre y el agua, se calcula la temperatura final.

Contestar

La temperatura final (alcanzada tanto por el cobre como por el agua) es de 38.7 °C.

Este método también se puede utilizar para determinar otras cantidades, como el calor específico de un metal desconocido.

Ejemplo\(\PageIndex{2}\): Identifying a Metal by Measuring Specific Heat

Una pieza de 59.7 g de metal que había sido sumergida en agua hirviendo se transfirió rápidamente a 60.0 mL de agua inicialmente a 22.0 °C. La temperatura final es de 28.5 °C. Utilice estos datos para determinar el calor específico del metal. Usa este resultado para identificar el metal.

Solución

Suponiendo una transferencia de calor perfecta, el calor desprendido por el metal = −calor absorbido por el agua, o:

\[q_\ce{metal}=−q_\ce{water} \nonumber \]

En forma expandida, esto es:

\[c_\ce{metal}×m_\ce{metal}×(T_\mathrm{f,metal}−T_\mathrm{i, metal})=−c_\ce{water}×m_\ce{water}×(T_\mathrm{f,water}−T_\mathrm{i,water}) \nonumber \]

Señalando que dado que el metal se sumergió en agua hirviendo, su temperatura inicial fue de 100.0 °C; y que para el agua, 60.0 mL = 60.0 g; tenemos:

\[\mathrm{(\mathit c_{metal})(59.7\:g)(28.5°C−100.0°C)=−(4.18\:J/g\: °C)(60.0\:g)(28.5°C−22.0°C)} \nonumber \]

Resolviendo esto:

\[\mathrm{\mathit c_{metal}=\dfrac{−(4.184\:J/g\: °C)(60.0\:g)(6.5°C)}{(59.7\:g)(−71.5°C)}=0.38\:J/g\: °C} \nonumber \]

Comparando esto con los valores del Cuadro T4, nuestro calor específico experimental es el más cercano al valor para el cobre (0.39 J/g °C), por lo que identificamos el metal como cobre.

Ejercicio\(\PageIndex{2}\)

Una pieza de 92.9-g de metal plata/gris se calienta a 178.0 °C y luego se transfiere rápidamente a 75.0 mL de agua inicialmente a 24.0 °C. Después de 5 minutos, tanto el metal como el agua han alcanzado la misma temperatura: 29.7 °C. Determinar el calor específico y la identidad del metal. (Nota: Debe encontrar que el calor específico es cercano al de dos metales diferentes. Explique cómo se puede determinar con confianza la identidad del metal).

Contestar

\(c_{metal}= 0.13 \;J/g\; °C\)

Este calor específico es cercano al del oro o al plomo. Sería difícil determinar qué metal se basaba únicamente en los valores numéricos. Sin embargo, la observación de que el metal es plata/gris además del valor para el calor específico indica que el metal es plomo.

 

Cuando utilizamos calorimetría para determinar el calor involucrado en una reacción química, se aplican los mismos principios que hemos estado discutiendo. La cantidad de calor absorbido por el calorímetro suele ser lo suficientemente pequeña como para que podamos descuidarlo (aunque no para mediciones de alta precisión, como se discutirá más adelante), y el calorímetro minimiza el intercambio de energía con el entorno. Debido a que la energía no se crea ni se destruye durante una reacción química, no hay ningún cambio general de energía durante la reacción. El calor producido o consumido en la reacción (el “sistema”), q _reacción, más el calor absorbido o perdido por la solución (el “entorno”),\(q_{solution}\), debe sumar hasta cero:

\[q_\ce{reaction}+q_\ce{solution}=0\ \label{ 5.3.10} \]

Esto significa que la cantidad de calor producido o consumido en la reacción es igual a la cantidad de calor absorbido o perdido por la solución:

\[q_\ce{reaction}=−q_\ce{solution} \label{5.3.11} \]

Este concepto se encuentra en el centro de todos los problemas y cálculos de calorimetría.

Ejemplo\(\PageIndex{3}\): Heat Produced by an Exothermic Reaction

Cuando se añaden 50.0 mL de HCl (aq) 0.10 M y 50.0 mL de NaOH 1.00 M (aq), ambos a 22.0 °C, a un calorímetro de taza de café, la temperatura de la mezcla alcanza un máximo de 28.9 °C ¿Cuál es la cantidad aproximada de calor que produce esta reacción?

\[\ce{HCl}(aq)+\ce{NaOH}(aq)⟶\ce{NaCl}(aq)+\ce{H2O}(l) \nonumber \]

S olución

Para visualizar lo que está pasando, imagina que podrías combinar las dos soluciones tan rápido que no tuvo lugar ninguna reacción mientras se mezclaban; luego después de mezclarlas, se produjo la reacción. Al instante de la mezcla, se tienen 100.0 mL de una mezcla de HCl y NaOH a 22.0 °C. El HCl y NaOH reaccionan luego hasta que la temperatura de la solución alcanza los 28.9 °C.

El calor desprendido por la reacción es igual al absorbido por la solución. Por lo tanto:

\[q_\ce{reaction}=−q_\ce{solution} \nonumber \]

(Es importante recordar que esta relación sólo se mantiene si el calorímetro no absorbe ningún calor de la reacción, y no hay intercambio de calor entre el calorímetro y su entorno).

A continuación, sabemos que el calor absorbido por la solución depende de su calor específico, masa y cambio de temperatura:

\[q_\ce{solution}=(c×m×ΔT)_\ce{solution} \nonumber \]

Para proceder con este cálculo, necesitamos hacer algunas suposiciones o aproximaciones más razonables. Dado que la solución es acuosa, podemos proceder como si fuera agua en términos de sus valores específicos de calor y masa. La densidad del agua es aproximadamente 1.0 g/mL, por lo que 100.0 mL tiene una masa de aproximadamente 1.0 × 10 ² g (dos cifras significativas). El calor específico del agua es aproximadamente 4.18 J/g °C, por lo que lo usamos para el calor específico de la solución. Sustituyendo estos valores da:

\[\mathrm{\mathit q_{solution}=(4.184\:J/g\: °C)(1.0×10^2\:g)(28.9°C−22.0°C)=2.89×10^3\:J} \nonumber \]

Por último, como estamos tratando de encontrar el calor de la reacción, tenemos:

\[q_\ce{reaction}=−q_\ce{solution}=−2.89×10^3\:J \nonumber \]

El signo negativo indica que la reacción es exotérmica. Produce 2.89 kJ de calor.

Ejercicio\(\PageIndex{3}\)

Cuando se mezclan 100 mL de NaCl (ac) 0.200 M y 100 mL de AgnO ₃ (aq) 0.200 M, ambos a 21.9 °C, en un calorímetro de taza de café, la temperatura aumenta a 23.5 °C a medida que se forma AgCl sólido. ¿Cuánto calor produce esta reacción de precipitación? ¿Qué suposiciones hiciste para determinar tu valor?

Contestar

\(1.34 \times 10^3\; J\); supongamos que no hay calor absorbido por el calorímetro, no se intercambia calor entre el calorímetro y su entorno, y que el calor específico y la masa de la solución son los mismos que los del agua

Termoquímica de Calentadores de Manos

Cuando trabaje o juegue al aire libre en un día frío, puede usar un calentador de manos para calentarse las manos (Figura\(\PageIndex{5}\)). Un calentador de manos reutilizable común contiene una solución sobresaturada de NaC ₂ H ₃ O ₂ (acetato de sodio) y un disco de metal. Doblar el disco crea sitios de nucleación alrededor de los cuales el NaC metaestable _{2 H 3 O 2} cristaliza rápidamente (un capítulo posterior sobre soluciones investigará la saturación y sobresaturación con más detalle).

El proceso\(\ce{NaC2H3O2}(aq)⟶\ce{NaC2H3O2}(s)\) es exotérmico, y el calor producido por este proceso es absorbido por tus manos, calentándolas así (al menos por un tiempo). Si se recalienta el calentador de manos, el NaC ₂ H ₃ O ₂ se vuelve a disolver y se puede reutilizar.

Figura\(\PageIndex{5}\): Los calentadores de manos químicos producen calor que calienta tu mano en un día frío. En este, se puede ver el disco metálico que inicia la reacción de precipitación exotérmica. (crédito: modificación de obra de Science Buddies TV/YouTube)

Se muestra una serie de tres fotos. Hay dos flechas orientadas hacia la derecha que conectan una foto con la siguiente. La primera foto muestra un calentador de manos químico. Se trata de una bolsa que contiene un líquido transparente e incoloro. Hay un disco blanco ubicado a la derecha dentro de la bolsa. La segunda foto muestra lo mismo, excepto que el disco blanco se ha convertido en una sustancia blanca, turbia. La tercera foto muestra toda la bolsa llena de esta sustancia blanca.

Otro calentador de manos común produce calor cuando se rasga, exponiendo el hierro y el agua en el calentador de manos al oxígeno en el aire. Una versión simplificada de esta reacción exotérmica es

\[\ce{2Fe(s) + 3/2 O2(g) ⟶ Fe2O3(s)}.\ n\nonumber \]

La sal en el calentador de manos cataliza la reacción, por lo que produce calor más rápidamente; la celulosa, la vermiculita y el carbón activado ayudan a distribuir el calor de manera uniforme. Otros tipos de calentadores de manos utilizan fluido para encendedor (un catalizador de platino ayuda a que el líquido más ligero se oxida exotérmicamente), carbón vegetal (el carbón se oxida en un caso especial) o unidades eléctricas que producen calor al pasar una corriente eléctrica de una batería a través de cables resistivos.

Ejemplo\(\PageIndex{4}\): Heat Flow in an Instant Ice Pack

Cuando el nitrato de amonio sólido se disuelve en agua, la solución se enfría. Esta es la base para una “bolsa de hielo instantánea” (Figura\(\PageIndex{5}\)). Cuando 3.21 g de NH ₄ NO ₃ sólido se disuelve en 50.0 g de agua a 24.9 °C en un calorímetro, la temperatura disminuye a 20.3 °C.

Calcular el valor de q para esta reacción y explicar el significado de su signo aritmético. Indique cualquier suposición que haya hecho.

Figura\(\PageIndex{5}\): Un paquete frío instantáneo consiste en una bolsa que contiene nitrato amónico sólido y una segunda bolsa de agua. Cuando se rompe la bolsa de agua, el paquete se enfría debido a que la disolución del nitrato de amonio es un proceso endotérmico que elimina la energía térmica del agua. La bolsa fría luego elimina la energía térmica de tu cuerpo.

Solución

Suponemos que el calorímetro impide la transferencia de calor entre la solución y su entorno externo (incluido el propio calorímetro), en cuyo caso:

\[q_\ce{rxn}=−q_\ce{soln} \nonumber \]

con “rxn” y “soln” utilizados como taquigrafía para “reacción” y “solución”, respectivamente.

Suponiendo también que el calor específico de la solución es el mismo que el del agua, tenemos:

\[\begin{align*} q_\ce{rxn} &=−q_\ce{soln}=−(c×m×ΔT)_\ce{soln}\\ &=\mathrm{−[(4.184J/g\: °C)×(53.2\:g)×(20.3°C−24.9°C)]}\\ &=\mathrm{−[(4.184J/g\: °C)×(53.2\:g)×(−4.6°C)]}\\ &+\mathrm{1.0×10^3\:J=+1.0\:kJ} \end{align*}\]

El signo positivo para q indica que la disolución es un proceso endotérmico.

Ejercicio\(\PageIndex{4}\)

Cuando se añadió una muestra de 3.00-g de KCl a 3.00 × 10 ² g de agua en un calorímetro de taza de café, la temperatura disminuyó 1.05 °C. ¿Cuánto calor implica la disolución del KCl? ¿Qué suposiciones hiciste?

Contestar

1.33 kJ; supongamos que el calorímetro impide la transferencia de calor entre la solución y su ambiente externo (incluido el propio calorímetro) y que el calor específico de la solución es el mismo que el del agua.

Si la cantidad de calor absorbido por un calorímetro es demasiado grande para descuidar o si requerimos resultados más precisos, entonces debemos tomar en cuenta el calor absorbido tanto por la solución como por el calorímetro.

Figura\(\PageIndex{6}\): (a) Se utiliza un calorímetro de bomba para medir el calor producido por reacciones que involucran reactivos gaseosos o productos, como la combustión. b) Los reactivos están contenidos en la “bomba” estanca al gas, la cual está sumergida en agua y rodeada de materiales aislantes. (crédito a: modificación de obra por “Harbor1” /Wikimedia commons)

Se muestran una imagen y un diagrama, etiquetados a y b, respectivamente. La imagen a representa un calorímetro de bomba. Se trata de una máquina en forma de cubo con una cavidad en la parte superior, un cilindro metálico que está por encima de la cavidad y un panel de lectura unido al lado superior derecho. El diagrama b representa una figura cortada de un cubo con un recipiente cilíndrico lleno de agua en medio del mismo. Otro recipiente, etiquetado como “bomba”, se encuentra dentro de un cilindro más pequeño que sostiene una taza de muestra y está anidado en el recipiente cilíndrico rodeado por el agua. Una línea negra se extiende hacia el agua y está etiquetada como “Termómetro de precisión”. Dos cables etiquetados como “Electrodos” se extienden lejos de una cubierta que se encuentra en la parte superior del contenedor interior. Un panel de lectura se encuentra en la parte superior derecha del cubo.

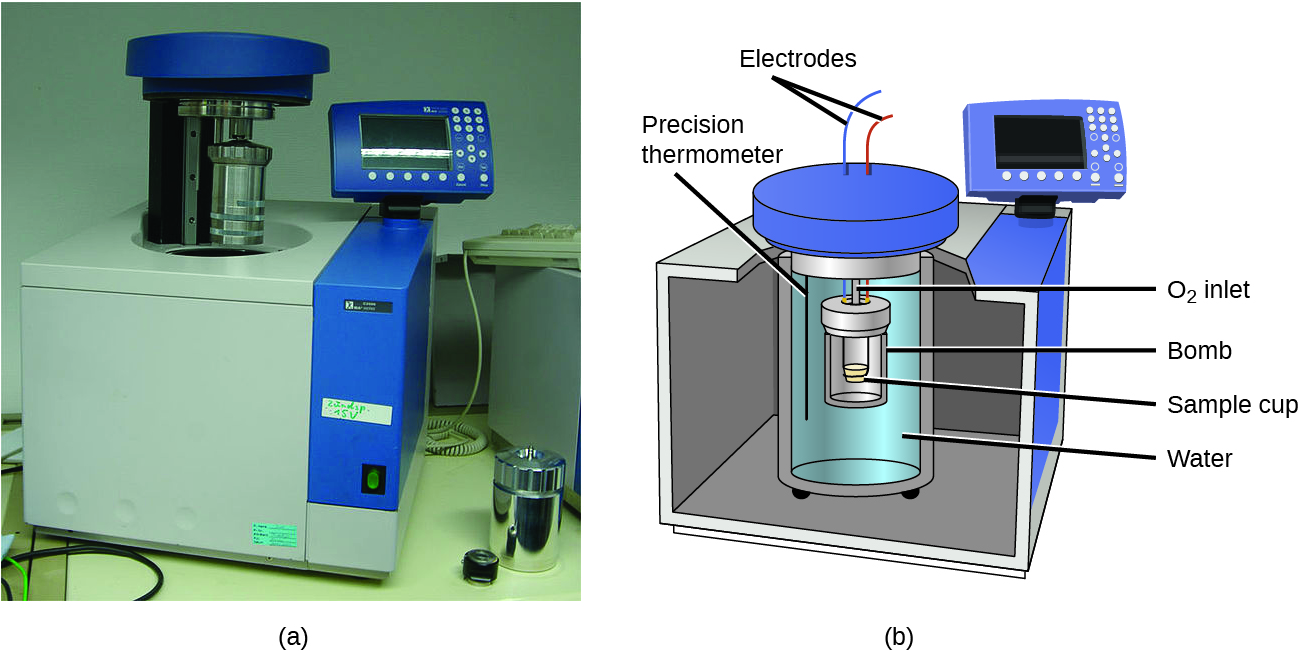
Los calorímetros descritos están diseñados para operar a presión constante (atmosférica) y son convenientes para medir el flujo de calor que acompaña a los procesos que ocurren en solución. Un tipo diferente de calorímetro que opera a volumen constante, conocido coloquialmente como calorímetro de bomba, se utiliza para medir la energía producida por reacciones que producen grandes cantidades de calor y productos gaseosos, como las reacciones de combustión. (El término “bomba” proviene de la observación de que estas reacciones pueden ser lo suficientemente vigorosas como para parecerse a explosiones que dañarían otros calorímetros). Este tipo de calorímetro consiste en un robusto contenedor de acero (la “bomba”) que contiene los reactivos y está a su vez sumergido en agua (Figura\(\PageIndex{6}\)). La muestra se coloca en la bomba, que luego se llena con oxígeno a alta presión. Se utiliza una pequeña chispa eléctrica para encender la muestra. La energía producida por la reacción queda atrapada en la bomba de acero y en el agua circundante. Se mide el incremento de temperatura y, junto con la capacidad calorífica conocida del calorímetro, se utiliza para calcular la energía producida por la reacción. Los calorímetros de bombas requieren calibración para determinar la capacidad calorífica del calorímetro y garantizar resultados precisos. La calibración se realiza usando una reacción con un q conocido, tal como una cantidad medida de ácido benzoico encendida por una chispa de un cable fusible de níquel que se pesa antes y después de la reacción. El cambio de temperatura producido por la reacción conocida se utiliza para determinar la capacidad calorífica del calorímetro. La calibración generalmente se realiza cada vez antes de que se utilice el calorímetro para recopilar datos de investigación.

Video\(\PageIndex{1}\): Video de vista cómo se prepara un calorímetro de bomba para la acción.

Ejemplo\(\PageIndex{5}\): Bomb Calorimetry

Cuando se queman 3.12 g de glucosa, C _{6 H 12 O 6}, en un calorímetro de bomba, la temperatura del calorímetro aumenta de 23.8 °C a 35.6 °C. El calorímetro contiene 775 g de agua, y la bomba en sí tiene una capacidad calorífica de 893 J/°C. ¿Cuánto calor produjo el combustión de la muestra de glucosa?

Solución

La combustión produce calor que es absorbido principalmente por el agua y la bomba. (Las cantidades de calor absorbidas por los productos de reacción y el exceso de oxígeno sin reaccionar son relativamente pequeñas y tratar con ellos está fuera del alcance de este texto. Los vamos a descuidar en nuestros cálculos.)

El calor producido por la reacción es absorbido por el agua y la bomba:

\ [\ begin {alinear*}
&q_\ ce {rxn} =− (q_\ ce {agua} +q_\ ce {bomba})\\
&=\ mathrm {− [(4.184\ :J/g\: °C) × (775\ :g) × (35.6°C−23.8°C) +893\ :J/°C× (35.6°C−23.8°C)]}\\
&=\ mathrm {− (38.300\ :J+10.500\ :J)}\\
&=\ mathrm {−48,800\: J=−48.8\: kJ}
\ end { alinear*}\ nonumber\]

Esta reacción liberó 48.7 kJ de calor cuando se quemaron 3.12 g de glucosa.

Ejercicio\(\PageIndex{5}\)

Cuando 0.963 g de benceno, C ₆ H ₆, se queman en un calorímetro de bomba, la temperatura del calorímetro aumenta 8.39 °C La bomba tiene una capacidad calorífica de 784 J/°C y se sumerge en 925 mL de agua. ¿Cuánto calor se produjo por la combustión de la muestra de glucosa?

Contestar

39.0 kJ

Desde que se construyó el primero en 1899, se han construido 35 calorímetros para medir el calor producido por una persona viva. ¹ Estos calorímetros de cuerpo entero de diversos diseños son lo suficientemente grandes como para albergar a un ser humano individual. Más recientemente, los calorímetros de toda la habitación permiten realizar actividades relativamente normales, y estos calorímetros generan datos que reflejan más de cerca el mundo real. Estos calorímetros se utilizan para medir el metabolismo de individuos bajo diferentes condiciones ambientales, diferentes regímenes dietéticos, y con diferentes condiciones de salud, como la diabetes. En humanos, el metabolismo se mide típicamente en Calorías por día. Una caloría nutricional (Calorías) es la unidad de energía utilizada para cuantificar la cantidad de energía derivada del metabolismo de los alimentos; una Caloría es igual a 1000 calorías (1 kcal), la cantidad de energía necesaria para calentar 1 kg de agua por 1 °C.

Medición de Calorías Nutricionales

En tu día a día, es posible que estés más familiarizado con la energía que se le da en Calorías, o calorías nutricionales, que se utilizan para cuantificar la cantidad de energía en los alimentos. Una caloría (cal) = exactamente 4.184 julios, y una Calorías (tenga en cuenta las mayúsculas) = 1000 cal, o 1 kcal. (Esta es aproximadamente la cantidad de energía necesaria para calentar 1 kg de agua por 1 °C).

Los macronutrientes en los alimentos son proteínas, carbohidratos y grasas o aceites. Las proteínas proporcionan alrededor de 4 Calorías por gramo, los carbohidratos también proporcionan aproximadamente 4 Calorías por gramo, y las grasas y aceites proporcionan alrededor de 9 calorías/g. Las etiquetas nutricionales en los paquetes de alimentos muestran el contenido calórico de una porción del alimento, así como el desglose en Calorías de cada uno de los tres macronutrientes ( Figura\(\PageIndex{7}\)).

Figura\(\PageIndex{7}\): a) Los macarrones y queso contienen energía en forma de macronutrientes en el alimento. b) La información nutricional del alimento se muestra en la etiqueta del envase. En EU, el contenido energético se da en Calorías (por porción); el resto del mundo suele utilizar kilojulios. (crédito a: modificación de obra por “Rex Roof” /Flickr)

Para el ejemplo que se muestra en (b), la energía total por porción de 228 g se calcula por:

\[\mathrm{(5\:g\: protein×4\:Calories/g)+(31\:g\: carb×4\:Calories/g)+(12\:g\: fat×9\:Calories/g)=252\:Calories} \label{5.3.X} \]

Entonces, puedes usar etiquetas de alimentos para contar tus Calorías. Pero, ¿de dónde vienen los valores? ¿Y qué tan precisos son? El contenido calórico de los alimentos se puede determinar mediante calorimetría de bomba; es decir, quemando los alimentos y midiendo la energía que contiene. Se pesa una muestra de alimento, se mezcla en una licuadora, se liofiliza, se muele en polvo y se conforma en un pellet. El pellet se quema dentro de un calorímetro de bomba, y el cambio de temperatura medido se convierte en energía por gramo de alimento.

Hoy en día, el contenido calórico en las etiquetas de los alimentos se deriva mediante un método llamado sistema Atwater que utiliza el contenido calórico promedio de los diferentes componentes químicos de los alimentos, proteínas, carbohidratos y grasas. Las cantidades promedio son las dadas en la ecuación y se derivan de los diversos resultados dados por la calorimetría de bomba de alimentos integrales. La cantidad de carbohidratos se descuenta una cierta cantidad por el contenido de fibra, que es carbohidrato indigerible. Para determinar el contenido energético de un alimento, las cantidades de carbohidratos, proteínas y grasas se multiplican cada una por el promedio de Calorías por gramo para cada uno y los productos se suman para obtener la energía total.

Resumen

La calorimetría se utiliza para medir la cantidad de energía térmica transferida en un proceso químico o físico. Esto requiere una cuidadosa medición del cambio de temperatura que se produce durante el proceso y las masas del sistema y alrededores. Estas cantidades medidas se utilizan para calcular la cantidad de calor producido o consumido en el proceso usando relaciones matemáticas conocidas. Los calorímetros están diseñados para minimizar el intercambio de energía entre el sistema que se estudia y su entorno. Abarcan desde simples calorímetros de taza de café utilizados por estudiantes de química introductoria hasta sofisticados calorímetros de bombas utilizados para determinar el contenido energético de los alimentos.

Notas al pie

1. 1 Francis D. Reardon y col. “El calorímetro humano Snellen revisó, rediseñó y actualizó: Características de diseño y rendimiento”. Ingeniería Médica y Biológica y Computación 8 (2006) 721—28, El calorímetro humano Snellen revisitado, rediseñado y actualizado: características de diseño y rendimiento [link.springer.com].

Glosario

calorímetro de bomba

dispositivo diseñado para medir el cambio de energía para procesos que ocurren en condiciones de volumen constante; comúnmente utilizado para reacciones que involucran reactivos o productos sólidos y gaseosos

calorímetro

dispositivo utilizado para medir la cantidad de calor absorbido o liberado en un proceso químico o físico

calorimetría

proceso de medición de la cantidad de calor involucrado en un proceso químico o físico

calorías nutricionales (Calorías)

unidad utilizada para cuantificar la energía proporcionada por la digestión de los alimentos, definida como 1000 cal o 1 kcal

alrededores

toda la materia que no sea el sistema en estudio

sistema

porción de materia sometida a un cambio químico o físico en estudio