5.3: Entalpía

Objetivos de aprendizaje

• Estado la primera ley de la termodinámica
• Definir la entalpía y explicar su clasificación como función de estado
• Escribir y equilibrar ecuaciones termoquímicas
• Calcular los cambios de entalpía para diversas reacciones químicas
• Explicar la ley de Hess y utilizarla para calcular entalpías de reacción

La termoquímica es una rama de la termodinámica química, la ciencia que se ocupa de las relaciones entre el calor, el trabajo y otras formas de energía en el contexto de los procesos químicos y físicos. A medida que nos concentramos en la termoquímica en este capítulo, debemos considerar algunos conceptos ampliamente utilizados de termodinámica.

Las sustancias actúan como reservorios de energía, es decir, que la energía puede agregarse a ellas o eliminarse de ellas. La energía se almacena en una sustancia cuando se eleva la energía cinética de sus átomos o moléculas. La mayor energía cinética puede estar en forma de mayores traslaciones (movimientos de desplazamiento o de línea recta), vibraciones o rotaciones de los átomos o moléculas. Cuando se pierde la energía térmica, las intensidades de estos movimientos disminuyen y la energía cinética disminuye. El total de todos los tipos posibles de energía presentes en una sustancia se llama la energía interna (U), a veces simbolizada como E.

A medida que un sistema sufre un cambio, su energía interna puede cambiar, y la energía se puede transferir del sistema al entorno, o del entorno al sistema. La energía se transfiere a un sistema cuando absorbe calor (q) del entorno o cuando el entorno trabaja (w) en el sistema. Por ejemplo, la energía se transfiere al alambre metálico a temperatura ambiente si se sumerge en agua caliente (el cable absorbe el calor del agua), o si dobla rápidamente el cable hacia adelante y hacia atrás (el cable se vuelve más cálido debido al trabajo realizado en él). Ambos procesos aumentan la energía interna del cable, lo que se refleja en un aumento en la temperatura del cable. Por el contrario, la energía se transfiere fuera de un sistema cuando se pierde calor del sistema, o cuando el sistema funciona en el entorno.

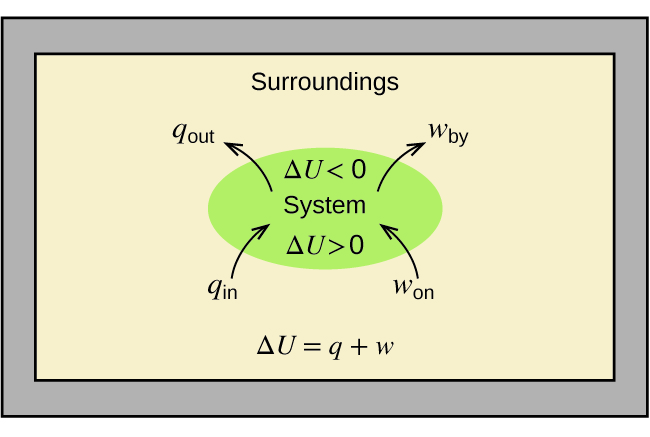
La relación entre la energía interna, el calor y el trabajo se puede representar por la ecuación:

\[ΔU=q+w \label{5.4.1} \]

como se muestra en la Figura\(\PageIndex{1}\). Esta es una versión de la primera ley de la termodinámica, y muestra que la energía interna de un sistema cambia a través del flujo de calor dentro o fuera del sistema (q positivo es flujo de calor adentro; negativo q es flujo de calor hacia afuera) o trabajo realizado en o por el sistema. El trabajo, w, es positivo si se realiza en el sistema y negativo si lo realiza el sistema.

Figura\(\PageIndex{1}\): La energía interna, U, de un sistema se puede cambiar por flujo de calor y trabajo. Si el calor fluye hacia el sistema, q _in, o se trabaja en el sistema, w _on, su energía interna aumenta, ΔU > 0. Si el calor fluye fuera del sistema, q _sale, o el trabajo es realizado por el sistema, w _by, su energía interna disminuye, ΔU < 0.

Un tipo de trabajo llamado trabajo de expansión (o trabajo de presión-volumen) ocurre cuando un sistema empuja hacia atrás el entorno contra una presión de restricción, o cuando el entorno comprime el sistema. Un ejemplo de esto ocurre durante el funcionamiento de un motor de combustión interna. La reacción de la gasolina y el oxígeno es exotérmica. Parte de esta energía se emite como calor, y algunos sí funcionan empujando el pistón en el cilindro. Las sustancias involucradas en la reacción son el sistema, y el motor y el resto del universo son los alrededores. El sistema pierde energía tanto calentando como realizando trabajos en el entorno, y su energía interna disminuye. (El motor es capaz de mantener el automóvil en movimiento porque este proceso se repite muchas veces por segundo mientras el motor está funcionando). Consideraremos cómo determinar la cantidad de trabajo involucrado en un cambio químico o físico en el capítulo sobre termodinámica.

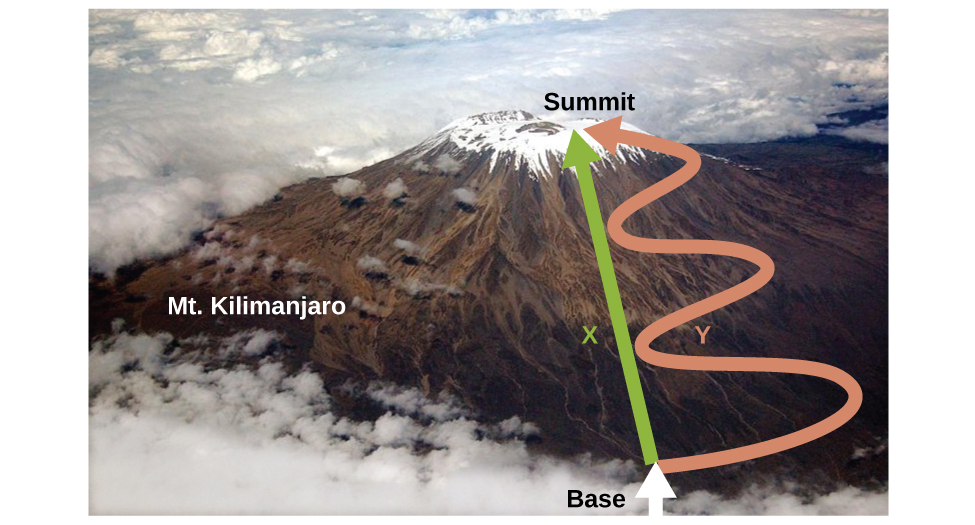
Como se discutió, la relación entre energía interna, calor y trabajo puede representarse como Δ U = q + w. La energía interna es un tipo de cantidad conocida como función de estado (o variable de estado), mientras que el calor y el trabajo no son funciones de estado. El valor de una función de estado depende únicamente del estado en el que se encuentra un sistema, y no de cómo se alcanza ese estado. Si una cantidad no es una función de estado, entonces su valor sí depende de cómo se alcance el estado. Un ejemplo de una función de estado es altitud o elevación. Si te paras en la cima del monte. Kilimanjaro, estás a una altitud de 5895 m, y no importa si caminaste allí o te lanzaste en paracaídas allí. La distancia que recorrías hasta la cima del Kilimanjaro, sin embargo, no es una función estatal. Se podría subir a la cima por una ruta directa o por una rotonda más, camino sinuoso (Figura\(\PageIndex{2}\)). Las distancias recorridas diferirían (la distancia no es una función de estado) pero la elevación alcanzada sería la misma (la altitud es una función de estado).

Figura\(\PageIndex{2}\): Los caminos X e Y representan dos rutas diferentes hacia la cima del monte. Kilimanjaro. Ambos tienen el mismo cambio de elevación (la altitud o elevación en una montaña es una función de estado; no depende del camino), pero tienen distancias recorridas muy diferentes (la distancia recorrida no es una función de estado; depende del camino). (crédito: modificación de obra de Paul Shaffner)

Una foto aérea representa una vista del monte Kilimanjaro. Una flecha recta, verde etiquetada como X, se dibuja desde el término “base”, escrito en la parte inferior de la montaña, hasta el término “Cumbre”, escrito en la cima de la montaña. Otra flecha etiquetada con Y es dibujar desde la base hasta la cumbre junto a la flecha verde, pero esta flecha es de color rosa y tiene tres grandes curvas en forma de S a lo largo de su longitud.

Los químicos suelen utilizar una propiedad conocida como entalpía (\(H\)) para describir la termodinámica de los procesos químicos y físicos. La entalpía se define como la suma de la energía interna de un sistema (\(U\)) y el producto matemático de su presión (\(P\)) y volumen (\(V\)):

\[H=U+PV \label{5.4.2} \]

Dado que se deriva de tres funciones de estado (\(U\),\(P\), y\(V\)), la entalpía también es una función de estado. Los valores de entalpía para sustancias específicas no se pueden medir directamente; solo se pueden determinar los cambios de entalpía para procesos químicos o físicos. Para los procesos que tienen lugar a presión constante (una condición común para muchos cambios químicos y físicos), el cambio de entalpía (\(ΔH\)) es:

\[ΔH=ΔU+PΔV\label{5.4.3} \]

El producto matemático\(PΔV\) representa el trabajo (\(w\)), es decir, el trabajo de expansión o presión-volumen como se señaló. Por sus definiciones, los signos aritméticos de ΔV y w siempre serán opuestos:

\[PΔV=−w \label{5.4.4} \]

Sustituyendo la Ecuación\ ref {5.4.4} y la definición de energía interna (Ecuación\ ref {5.4.1}) en la Ecuación\ ref {5.4.3} produce:

\[ \begin{align} ΔH&=ΔU+PΔV \\[4pt] &=q_\ce{p}+\cancel{w}−\cancel{w} \\[4pt] &=q_\ce{p} \label{5.4.5} \end{align} \]

donde\(q_p\) está el calor de reacción bajo condiciones de presión constante.

Y así, si se realiza un proceso químico o físico a presión constante con el único trabajo realizado causado por la expansión o contracción, entonces el flujo de calor (\(q_\ce{p}\)) y el cambio de entalpía (\(ΔH\)) para el proceso son iguales.

El calor desprendido cuando se opera un quemador Bunsen es igual al cambio de entalpía de la reacción de combustión de metano que tiene lugar, ya que ocurre a la presión esencialmente constante de la atmósfera. Por otro lado, el calor producido por una reacción medida en un calorímetro de bomba no es igual a\(ΔH\) porque el contenedor metálico cerrado de volumen constante evita que se produzcan trabajos de expansión. Los químicos suelen realizar experimentos en condiciones atmosféricas normales, a presión externa constante con\(q = ΔH\), lo que hace que la entalpía sea la opción más conveniente para determinar el calor.

Las siguientes convenciones se aplican cuando utilizamos\(ΔH\):

1. Los químicos utilizan una ecuación termoquímica para representar los cambios tanto en materia como en energía. En una ecuación termoquímica, el cambio de entalpía de una reacción se muestra como un valor ΔH siguiendo la ecuación para la reacción. Este\(ΔH\) valor indica la cantidad de calor asociado a la reacción que implica el número de moles de reactivos y productos como se muestra en la ecuación química. Por ejemplo, considere esta ecuación:\[\ce{H2(g) + 1/2 O2(g) ⟶ H2O (l)} \;\; ΔH=\mathrm{−286\:kJ} \label{5.4.6} \] Esta ecuación indica que cuando 1 mol de gas hidrógeno y 12 mol de gas oxígeno a cierta temperatura y presión cambian a 1 mol de agua líquida a la misma temperatura y presión, 286 kJ de calor son liberados a los alrededores. Si los coeficientes de la ecuación química se multiplican por algún factor, el cambio de entalpía debe multiplicarse por ese mismo factor (ΔH es una propiedad extensa).

\[\begin {align*} &\textrm{(two-fold increase in amounts)}\label{5.4.7}\\ &\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(l)\hspace{20px}ΔH=\mathrm{2×(−286\:kJ)=−572\:kJ}\\ &\textrm{(two-fold decrease in amounts)}\\ &\frac{1}{2}\ce{H2}(g)+\dfrac{1}{4}\ce{O2}(g)⟶\frac{1}{2}\ce{H2O}(l)\hspace{20px}ΔH=\mathrm{\frac{1}{2}×(−286\:kJ)=−143\:kJ} \end {align*} \label{5.4.6B} \]

2. El cambio de entalpía de una reacción depende del estado físico de los reactivos y productos de la reacción (ya sea que tengamos gases, líquidos, sólidos o soluciones acuosas), por lo que estos deben mostrarse. Por ejemplo, cuando 1 mol de gas hidrógeno y 12 mol de gas oxígeno cambian a 1 mol de agua líquida a la misma temperatura y presión, se liberan 286 kJ de calor. Si se forma agua gaseosa, solo se liberan 242 kJ de calor.

\[\ce{ H2(g) + 1/2 O2(g) ⟶ H2O(g)} \;\;\; ΔH=\ce{−242\:kJ} \label{5.4.7B} \]

 

3. Un valor negativo de un cambio de entalpía, Δ H, indica una reacción exotérmica; un valor positivo de Δ H indica una reacción endotérmica. Si se invierte la dirección de una ecuación química, se cambia el signo aritmético de su Δ H (un proceso que es endotérmico en una dirección es exotérmico en la dirección opuesta).

Ejemplo\(\PageIndex{1}\): Measurement of an Enthalpy Change

Cuando 0.0500 mol de HCl (ac) reacciona con 0.0500 mol de NaOH (ac) para formar 0.0500 mol de NaCl (ac), se producen 2.9 kJ de calor. ¿Cuál es ΔH, el cambio de entalpía, por mol de ácido que reacciona, para la reacción ácido-base ejecutada en las condiciones descritas?

\[\ce{HCl (aq) + NaOH(aq) \rightarrow NaCl (aq) + H2O(l)} \nonumber \]

Solución

Para la reacción de 0.0500 mol de ácido (HCl), q = −2.9 kJ. Esta relación

\[\mathrm{\dfrac{−2.9 \; kJ}{0.0500\; mol\; HCl}} \nonumber \]

puede ser utilizado como factor de conversión para encontrar el calor producido cuando 1 mol de HCl reacciona:

\[ΔH =\mathrm{1\; \cancel{mol\; HCl} \times \dfrac{ −2.9\; kJ}{0.0500 \;\cancel{ mol\; HCl}} =−58\; kJ} \nonumber \]

El cambio de entalpía cuando reacciona 1 mol de HCl es −58 kJ. Dado que ese es el número de moles en la ecuación química, escribimos la ecuación termoquímica como:

\[\ce{HCl}_{(aq)}+\ce{NaOH}_{(aq)}⟶\ce{NaCl}_{(aq)}+\ce{H_2O}_{(l)} \;\;\; ΔH=\mathrm{−58\;kJ} \nonumber \]

Ejercicio\(\PageIndex{1}\)

Cuando 1.34 g Zn (s) reacciona con 60.0 mL de HCl (aq) 0.750 M, se producen 3.14 kJ de calor. Determinar el cambio de entalpía por mol de zinc que reacciona para la reacción:

\[ \ce{Zn}_{(s)}+\ce{2HCl}_{(aq)}⟶\ce{ZnCl}_{(aq)}+\ce{H}_{2(g)} \nonumber \]

Responder

ΔH = −153 kJ

Asegúrese de tener en cuenta tanto la estequiometría como los reactivos limitantes al determinar el Δ H para una reacción química.

Ejemplo\(\PageIndex{2}\): Another Example of the Measurement of an Enthalpy Change

Un oso gomoso contiene 2.67 g de sacarosa, C ₁₂ H ₂₂ O ₁₁. Cuando reacciona con 7.19 g de clorato de potasio, se producen KClO ₃, 43.7 kJ de calor. Determinar el cambio de entalpía para la reacción

\[\ce{C12H22O11}(aq)+\ce{8KClO3}(aq)⟶\ce{12CO2}(g)+\ce{11H2O}(l)+\ce{8KCl}(aq) \nonumber \]

S olución

Tenemos\(\mathrm{2.67\:\cancel{g}×\dfrac{1\:mol}{342.3\:\cancel{g}}=0.00780\:mol\:C_{12}H_{22}O_{11}}\) disponibles, y

\(\mathrm{7.19\:\cancel{g}×\dfrac{1\:mol}{122.5\:\cancel{g}}=0.0587\:mol\:KClO_3}\)disponibles.

Desde

\(\mathrm{0.0587\:mol\:KClO_3×\dfrac{1\:mol\:\ce{C12H22O11}}{8\:mol\:KClO_3}=0.00734\:mol\:\ce{C12H22O11}}\)

es necesario, C ₁₂ H ₂₂ O ₁₁ es el reactivo en exceso y KClO ₃ es el reactivo limitante.

La reacción utiliza 8 mol de KClO ₃, y el factor de conversión es\(\mathrm{\dfrac{−43.7\:kJ}{0.0587\:mol\:KClO_3}}\), así que tenemos\(ΔH=\mathrm{8\:mol×\dfrac{−43.7\:kJ}{0.0587\:mol\:KClO_3}=−5960\:kJ}\). El cambio de entalpía para esta reacción es −5960 kJ, y la ecuación termoquímica es:

\[\ce{C12H22O11 + 8KClO3⟶12CO2 + 11H2O + 8KCl}\hspace{20px}ΔH=\ce{−5960\:kJ} \nonumber \]

Ejercicio\(\PageIndex{2}\)

Cuando 1.42 g de hierro reacciona con 1.80 g de cloro, se producen 3.22 g de\(\ce{FeCl}_{2(s)}\) y 8.60 kJ de calor. ¿Cuál es el cambio de entalpía para la reacción cuando\(\ce{FeCl2(s)}\) se produce 1 mol de?

Responder

ΔH = −338 kJ

Los cambios de entalpía se tabulan típicamente para reacciones en las que tanto los reactivos como los productos están en las mismas condiciones. Un estado estándar es un conjunto de condiciones comúnmente aceptadas que se utilizan como punto de referencia para la determinación de propiedades bajo otras condiciones diferentes. Para los químicos, el estado estándar de la IUPAC se refiere a materiales bajo una presión de 1 bar y soluciones a 1 M, y no especifica una temperatura (también se usó). Muchas tablas termoquímicas enumeran valores con un estado estándar de 1 atm. Debido a que el Δ H de una reacción cambia muy poco con cambios tan pequeños en la presión (1 bar = 0.987 atm), los valores de Δ H (excepto los valores medidos con mayor precisión) son esencialmente los mismos en ambos conjuntos de condiciones estándar. Incluiremos una “o” en superíndice en el símbolo de cambio de entalpía para designar el estado estándar. Dado que la temperatura habitual (pero no técnicamente estándar) es de 298.15 K, utilizaremos un subíndice “298” para designar esta temperatura. Así, el símbolo (\(ΔH^\circ_{298}\)) se utiliza para indicar un cambio de entalpía para un proceso que ocurre bajo estas condiciones. (El símbolo Δ H se utiliza para indicar un cambio de entalpía para una reacción que ocurre en condiciones no estándar).

Los cambios de entalpía para muchos tipos de procesos químicos y físicos están disponibles en la literatura de referencia, incluyendo aquellos para reacciones de combustión, transiciones de fase y reacciones de formación. Al discutir estas cantidades, es importante prestar atención a la naturaleza extensa de los cambios de entalpía y entalpía. Dado que el cambio de entalpía para una reacción dada es proporcional a las cantidades de sustancias involucradas, se puede reportar sobre esa base (es decir, como el Δ H para cantidades específicas de reactivos). Sin embargo, a menudo encontramos más útil dividir una propiedad extensa (Δ H) por otra (cantidad de sustancia), y reportar un valor intensivo por cantidad de Δ H, a menudo “normalizado” a una base por mol. (Tenga en cuenta que esto es similar a determinar el calor específico de propiedad intensiva a partir de la capacidad de calor de propiedad extensa, como se vio anteriormente).

Entalpía de Combustión

La entalpía estándar de combustio n (\(ΔH_C^\circ\)) es el cambio de entalpía cuando 1 mol de una sustancia se quema (se combina vigorosamente con el oxígeno) en condiciones de estado estándar; a veces se le llama “calor de combustión”. Por ejemplo, la entalpía de combustión de etanol, −1366.8 kJ/mol, es la cantidad de calor que se produce cuando un mol de etanol se somete a combustión completa a 25 °C y 1 atmósfera de presión, produciendo productos también a 25 °C y 1 atm.

\[\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{2CO2}+\ce{3H2O}(l)\hspace{20px}ΔH_{298}^\circ=\mathrm{−1366.8\: kJ} \label{5.4.8} \]

Se han medido entalpías de combustión para muchas sustancias; algunas de estas se enumeran en la Tabla\(\PageIndex{1}\). Muchas sustancias fácilmente disponibles con grandes entalpías de combustión se utilizan como combustibles, incluyendo hidrógeno, carbono (como carbón o carbón vegetal) e hidrocarburos (compuestos que contienen solo hidrógeno y carbono), como el metano, propano y los principales componentes de la gasolina.

Tabla\(\PageIndex{1}\): Entalpías Molares Estándar de Combustión

Sustancia	Reacción de combustión	Entalpía de Combustión\(ΔH_c^\circ \left(\mathrm{\dfrac{kJ}{mol} \:at\:25°C}\right)\)
carbono	\(\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)\)	\ (ΔH_C^\ circ\ izquierda (\ mathrm {\ dfrac {kJ} {mol}\ :at\ :25°C}\ derecha)\)” style="text-align:center; ">−393.5
hidrógeno	\(\ce{H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{H2O}(l)\)	\ (ΔH_C^\ circ\ izquierda (\ mathrm {\ dfrac {kJ} {mol}\ :at\ :25°C}\ derecha)\)” style="text-align:center; ">−285.8
magnesio	\(\ce{Mg}(s)+\frac{1}{2}\ce{O2}(g)⟶\ce{MgO}(s)\)	\ (ΔH_C^\ circ\ izquierda (\ mathrm {\ dfrac {kJ} {mol}\ :at\ :25°C}\ derecha)\)” style="text-align:center; ">−601.6
azufre	\(\ce{S}(s)+\ce{O2}(g)⟶\ce{SO2}(g)\)	\ (ΔH_C^\ circ\ izquierda (\ mathrm {\ dfrac {kJ} {mol}\ :at\ :25°C}\ derecha)\)” style="text-align:center; ">−296.8
monóxido de carbono	\(\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO2}(g)\)	\ (ΔH_C^\ circ\ izquierda (\ mathrm {\ dfrac {kJ} {mol}\ :at\ :25°C}\ derecha)\)” style="text-align:center; ">−283.0
metano	\(\ce{CH4}(g)+\ce{2O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)\)	\ (ΔH_C^\ circ\ izquierda (\ mathrm {\ dfrac {kJ} {mol}\ :at\ :25°C}\ derecha)\)” style="text-align:center; ">−890.8
acetileno	\(\ce{C2H2}(g)+\dfrac{5}{2}\ce{O2}(g)⟶\ce{2CO2}(g)+\ce{H2O}(l)\)	\ (ΔH_C^\ circ\ izquierda (\ mathrm {\ dfrac {kJ} {mol}\ :at\ :25°C}\ derecha)\)” style="text-align:center; ">−1301.1
etanol	\(\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{CO2}(g)+\ce{3H2O}(l)\)	\ (ΔH_C^\ circ\ izquierda (\ mathrm {\ dfrac {kJ} {mol}\ :at\ :25°C}\ derecha)\)” style="text-align:center; ">−1366.8
metanol	\(\ce{CH3OH}(l)+\dfrac{3}{2}\ce{O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)\)	\ (ΔH_C^\ circ\ izquierda (\ mathrm {\ dfrac {kJ} {mol}\ :at\ :25°C}\ derecha)\)” style="text-align:center; ">−726.1
isooctano	\(\ce{C8H18}(l)+\dfrac{25}{2}\ce{O2}(g)⟶\ce{8CO2}(g)+\ce{9H2O}(l)\)	\ (ΔH_C^\ circ\ izquierda (\ mathrm {\ dfrac {kJ} {mol}\ :at\ :25°C}\ derecha)\)” style="text-align:center; ">−5461

Ejemplo\(\PageIndex{3}\): Using Enthalpy of Combustion

Como\(\PageIndex{3}\) sugiere la Figura, la combustión de la gasolina es un proceso altamente exotérmico. Determinemos la cantidad aproximada de calor producido al quemar 1.00 L de gasolina, asumiendo que la entalpía de combustión de la gasolina es la misma que la del isooctano, un componente común de la gasolina. La densidad de isooctano es de 0.692 g/mL.

Figura\(\PageIndex{3}\): La combustión de la gasolina es muy exotérmica. (crédito: modificación de obra por “AlexEagle” /Flickr)

Solución

Comenzando con una cantidad conocida (1.00 L de isooctano), podemos realizar conversiones entre unidades hasta llegar a la cantidad deseada de calor o energía. La entalpía de combustión de isooctano proporciona una de las conversiones necesarias. La tabla\(\PageIndex{1}\) da este valor como −5460 kJ por 1 mol de isooctano (C ₈ H ₁₈).

Utilizando estos datos,

\[\mathrm{1.00\:\cancel{L\:\ce{C8H18}}×\dfrac{1000\:\cancel{mL\:\ce{C8H18}}}{1\:\cancel{L\:\ce{C8H18}}}×\dfrac{0.692\:\cancel{g\:\ce{C8H18}}}{1\:\cancel{mL\:\ce{C8H18}}}×\dfrac{1\:\cancel{mol\:\ce{C8H18}}}{114\:\cancel{g\:\ce{C8H18}}}×\dfrac{−5460\:kJ}{1\:\cancel{mol\:\ce{C8H18}}}=−3.31×10^4\:kJ} \nonumber \]

La combustión de 1.00 L de isooctano produce 33,100 kJ de calor. (Esta cantidad de energía es suficiente para derretir 99.2 kg, o aproximadamente 218 lbs, de hielo).

Nota: Si haces este cálculo paso a paso, encontrarás:

\ (\ begin {alinear*}
&\ mathrm {1.00\ :L\:\ ce {C8H18} 1.00×10^3\ :ml\:\ ce {C8H18}}\\
&\ mathrm {1.00×10^3\ :ml\:\ ce {C8H18} 692\ :g\:\ ce {C8H18}}\
& mathrm {692\ :g\:\ ce {C8H18} 6.07\ :mol\:\ ce {C8H18}}\\
&\ mathrm {692\ :g\:\ ce {C8H18} −3.31×10^4\ :kJ}
\ end {alinear*}\)

Ejercicio\(\PageIndex{3}\)

¿Cuánto calor se produce por la combustión de 125 g de acetileno?

Responder

6.25 × 10 ³ kJ

Tecnologías Energéticas Emergentes Basadas en Algas (Biocombustibles)

A medida que las reservas de combustibles fósiles disminuyen y se vuelven más costosas de extraer, continúa la búsqueda de fuentes de combustible de reemplazo para el futuro. Entre los biocombustibles más prometedores se encuentran los derivados de algas (Figura\(\PageIndex{4}\)). Las especies de algas utilizadas son no tóxicas, biodegradables y se encuentran entre los organismos de más rápido crecimiento del mundo. Alrededor del 50% del peso de las algas es aceite, el cual se puede convertir fácilmente en combustible como el biodiesel. Las algas pueden producir 26,000 galones de biocombustible por hectárea, mucha más energía por acre que otros cultivos. Algunas cepas de algas pueden florecer en agua salobre que no es utilizable para cultivar otros cultivos. Las algas pueden producir biodiesel, biogasolina, etanol, butanol, metano e incluso combustible para aviones.

Figura\(\PageIndex{4}\): (a) Los organismos de algas diminutas pueden (b) cultivarse en grandes cantidades y eventualmente (c) convertirse en un combustible útil como el biodiesel. (crédito a: modificación de obra de Micah Sittig; crédito b: modificación de obra de Robert Kerton; crédito c: modificación de obra de John F. Williams)

Según el Departamento de Energía de Estados Unidos, solo 39,000 kilómetros cuadrados (alrededor del 0.4% de la masa terrestre de Estados Unidos o menos\(\dfrac{1}{7}\) de la superficie utilizada para cultivar maíz) pueden producir suficiente combustible de algas para reemplazar todo el combustible a base de petróleo que se usa en Estados Unidos. El costo de los combustibles de algas es cada vez más competitivo, por ejemplo, la Fuerza Aérea de Estados Unidos está produciendo combustible para aviones a partir de algas a un costo total de menos de 5 dólares por galón. El proceso utilizado para producir combustible de algas es el siguiente: cultivar las algas (que utilizan la luz solar como fuente de energía y CO ₂ como materia prima); cosechar las algas; extraer los compuestos combustibles (o compuestos precursores); procesar según sea necesario (por ejemplo, realizar una reacción de transesterificación para hacer biodiesel); purificar; y distribuir (Figura\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): Las algas convierten la luz solar y el dióxido de carbono en aceite que se cosecha, extrae, purifica y transforma en una variedad de combustibles renovables.

Entalpía Estándar de Formación

Una entalpía estándar de formación\(ΔH^\circ_\ce{f}\) es un cambio de entalpía para una reacción en la que exactamente 1 mol de una sustancia pura se forma a partir de elementos libres en sus estados más estables bajo condiciones de estado estándar. Estos valores son especialmente útiles para calcular o predecir cambios de entalpía para reacciones químicas poco prácticas o peligrosas de llevar a cabo, o para procesos para los que es difícil realizar mediciones. Si tenemos valores para las entalpías estándar apropiadas de formación, podemos determinar el cambio de entalpía para cualquier reacción, que practicaremos en la siguiente sección sobre la ley de Hess.

La entalpía estándar de formación de CO ₂ (g) es −393.5 kJ/mol. Este es el cambio de entalpía para la reacción exotérmica:

\[\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)\hspace{20px}ΔH^\circ_\ce{f}=ΔH^\circ_{298}=−393.5\:\ce{kJ} \label{5.4.9} \]

comenzando con los reactivos a una presión de 1 atm y 25 °C (con el carbono presente como grafito, la forma más estable de carbono bajo estas condiciones) y terminando con un mol de CO ₂, también a 1 atm y 25 °C. para dióxido de nitrógeno,\(\ce{NO}_{2(g)}\),\(ΔH^\circ_\ce{f}\) es 33.2 kJ/mol. Este es el cambio de entalpía para la reacción:

\[\frac{1}{2}\ce{N2}(g)+\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH^\circ_\ce{f}=ΔH^\circ_{298}=+33.2\: \ce{kJ} \label{5.4.10} \]

Una ecuación de reacción con\(\frac{1}{2}\) mol de N ₂ y 1 mol de O ₂ es correcta en este caso porque la entalpía estándar de formación siempre se refiere a 1 mol de producto, NO ₂ (g).

Encontrará una tabla de entalpías estándar de formación de muchas sustancias comunes en las Tablas T1 y T2. Estos valores indican que las reacciones de formación van desde altamente exotérmicas (como −2984 kJ/mol para la formación de P ₄ O ₁₀) hasta fuertemente endotérmicas (como +226.7 kJ/mol para la formación de acetileno, C ₂ H ₂). Por definición, la entalpía estándar de formación de un elemento en su forma más estable es igual a cero en condiciones estándar, que es 1 atm para gases y 1 M para soluciones.

Ejemplo\(\PageIndex{4}\): Evaluating an Enthalpy of Formation

El ozono, O ₃ (g), se forma a partir del oxígeno, O ₂ (g), por un proceso endotérmico. La radiación ultravioleta es la fuente de la energía que impulsa esta reacción en la atmósfera superior. Suponiendo que tanto los reactivos como los productos de la reacción se encuentran en sus estados estándar, determinar la entalpía estándar de formación,\(ΔH^\circ_\ce{f}\) del ozono a partir de la siguiente información:

\[\ce{3O2}(g)⟶\ce{2O3}(g)\hspace{20px}ΔH^\circ_{298}=+286\: \ce{kJ} \nonumber \]

S olutio n\(ΔH^\circ_\ce{f}\) es el cambio de entalpía para la formación de un mol de una sustancia en su estado estándar a partir de los elementos en sus estados estándar. Así,\(ΔH^\circ_\ce{f}\) para O ₃ (g) es el cambio de entalpía para la reacción:

\[\dfrac{3}{2}\ce{O2}(g)⟶\ce{O3}(g) \nonumber \]

Para la formación de 2 mol de O ₃ (g),\(ΔH^\circ_{298}=+286\: \ce{kJ}\). Esta relación,\(\mathrm{\left(\dfrac{286\:kJ}{2\:mol\:O_3}\right)}\), puede ser utilizada como factor de conversión para encontrar el calor producido cuando se forma 1 mol de O ₃ (g), que es la entalpía de formación para O ₃ (g):

\[ΔH^\circ \ce{\:for\:1\:mole\: of\:O_3}(g)=\mathrm{1\:\cancel{mol\:O_3}×\dfrac{286\:kJ}{2\:\cancel{mol\:O_3}}=143\:kJ} \nonumber \]

Por lo tanto,\(ΔH^\circ_\ce{f}[\ce{O3}(g)]=\ce{+143\: kJ/mol}\).

Ejercicio\(\PageIndex{4}\)

El gas hidrógeno, H ₂, reacciona explosivamente con cloro gaseoso, Cl ₂, para formar cloruro de hidrógeno, HCl (g). ¿Cuál es el cambio de entalpía para la reacción de 1 mol de H ₂ (g) con 1 mol de Cl ₂ (g) si tanto los reactivos como los productos están en condiciones de estado estándar? La entalpía estándar de formación de HCl (g) es −92.3 kJ/mol.

Responder

Para la reacción

\[\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH^\circ_{298}=\mathrm{−184.6\:kJ} \nonumber \]

Ejemplo\(\PageIndex{5}\): Writing Reaction Equations for \(ΔH^\circ_\ce{f}\)

Escriba las ecuaciones de reacción de calor de formación para:

1. \(\ce{C2H_5OH}_{(l)}\)
2. \(\ce{Ca_3(PO_4)}_{2(s)}\)

Solución

Recordando que las ecuaciones de\(ΔH^\circ_\ce{f}\) reacción son para formar 1 mol del compuesto a partir de sus elementos constituyentes en condiciones estándar, tenemos:

1. \(\ce{2C}(s,\:\ce{graphite})+\ce{3H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{C2H5OH}(l)\)
2. \(\ce{3Ca}(s)+\frac{1}{2}\ce{P4}(s)+\ce{4O2}(g)⟶\ce{Ca3(PO4)2}(s)\)

Nota: El estado estándar del carbono es el grafito, y el fósforo existe como\(P_4\).

Ejercicio\(\PageIndex{5}\)

Escriba las ecuaciones de reacción de calor de formación para:

1. \(\ce{C_2H_5OC_2H}_{5(l)}\)
2. \(\ce{Na_2CO}_{3(s)}\)

Contestar a

\(\ce{4C}(s,\:\ce{graphite})+\ce{5H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{C2H5OC2H5}(l)\);

Respuesta b

\(\ce{2Na}(s)+\ce{C}(s,\:\ce{graphite})+\dfrac{3}{2}\ce{O2}(g)⟶\ce{Na2CO3}(s)\)

Ley de Hess

Hay dos formas de determinar la cantidad de calor involucrada en un cambio químico: medirlo experimentalmente o calcularlo a partir de otros cambios de entalpía determinados experimentalmente. Algunas reacciones son difíciles, si no imposibles, de investigar y hacer mediciones precisas para experimentalmente. E incluso cuando una reacción no es difícil de realizar o medir, es conveniente poder determinar el calor involucrado en una reacción sin tener que realizar un experimento.

Este tipo de cálculo suele implicar el uso de la ley de Hess, que establece: Si un proceso puede escribirse como la suma de varios procesos paso a paso, el cambio de entalpía del proceso total equivale a la suma de los cambios de entalpía de los distintos pasos. La ley de Hess es válida porque la entalpía es una función de estado: los cambios de entalpía dependen solo de dónde comienza y termina un proceso químico, pero no del camino que toma de principio a fin. Por ejemplo, podemos pensar que la reacción del carbono con el oxígeno para formar dióxido de carbono ocurre ya sea directamente o mediante un proceso de dos etapas. El proceso directo está escrito:

\[\ce{C}_{(s)}+\ce{O}_{2(g)}⟶\ce{CO}_{2(g)}\;\;\;ΔH^∘_{298}=\mathrm{−394\;kJ} \label{ 5.4.11} \]

En el proceso de dos etapas, se forma el primer monóxido de carbono:

\[\ce{C}_{(s)}+\dfrac{1}{2}\ce{O}_{2(g)}⟶\ce{CO}_{(g)}\;\;\;ΔH^∘_{298}=\mathrm{−111\;kJ} \label{ 5.4.12} \]

Luego, el monóxido de carbono reacciona más para formar dióxido de carbono:

\[\ce{CO} {(g)}+\dfrac{1}{2}\ce{O2}(g)⟶\ce{CO}_2 {(g)}\;\;\;ΔH^∘_{298}=\mathrm{−283\;kJ} \label{ 5.4.13} \]

La ecuación que describe la reacción global es la suma de estos dos cambios químicos:

\[\begin {align*} &\textrm{Step 1:} \:\ce{C}(s)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO}(g)\\ &\underline{\textrm{Step 2:} \:\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO2}(g)}\\ &\textrm{Sum:} \:\ce{C}(s)+\frac{1}{2}\ce{O2}(g)+\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO}(g)+\ce{CO2}(g) \end {align*} \label{5.4.14} \]

Debido a que el CO producido en el Paso 1 se consume en el Paso 2, el cambio neto es:

\[\ce{C}_{(s)}+\ce{O}_{2(g)}⟶\ce{CO}_{2(g)} \label{5.4.15} \]

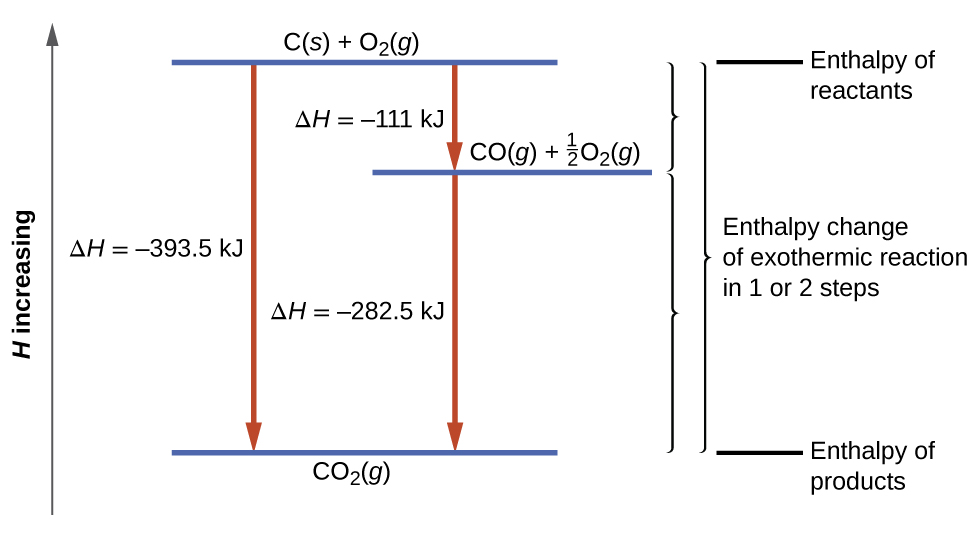
Según la ley de Hess, el cambio de entalpía de la reacción será igual a la suma de los cambios de entalpía de los pasos. Podemos aplicar los datos de las entalpías experimentales de combustión en la Tabla\(\PageIndex{1}\) para encontrar el cambio de entalpía de toda la reacción a partir de sus dos etapas:

\ [\ begin {alinear*}
&\ ce {C} (s) +\ frac {1} {2}\ ce {O2} (g) ⟶\ ce {CO} (g) &&ΔH^\ circ_ {298} =\ mathrm {−111\ :kJ}\\
&\ ce {CO} (g) +\ frac {1} {2}\ ce {O2} (g) ⟶\ ce {CO2} (g) &&ΔH^\ circ_ {298} =\ mathrm {−283\ :kJ}\\
&\ overline {\ ce {C} (s) +\ ce {O2} (g) ⟶\ ce {CO2} (g)\ hspace {25px}} & ; &\ overline {ΔH^\ circ_ {298} =\ mathrm {−394\ :kJ}}
\ end {align*}\ label {5.4.16}\]

El resultado se muestra en la Figura\(\PageIndex{6}\). Vemos que ΔH de la reacción global es la misma ya sea que ocurra en un paso o dos. Este hallazgo (ΔH global para la reacción = suma de los valores de Δ H para las “etapas” de reacción en la reacción general) es cierto en general para procesos químicos y físicos.

Figura\(\PageIndex{6}\): Se puede pensar que la formación de CO ₂ (g) a partir de sus elementos ocurre en dos etapas, que se suman a la reacción global, según lo descrito por la ley de Hess. Las líneas azules horizontales representan entalpías. Para un proceso exotérmico, los productos están a menor entalpía que los reactivos.

Antes de seguir practicando el uso de la ley de Hess, recordemos dos características importantes de Δ H.

1. Δ H es directamente proporcional a las cantidades de reactivos o productos. Por ejemplo, el cambio de entalpía para la reacción que forma 1 mol de NO ₂ (g) es +33.2 kJ:\[\frac{1}{2}\ce{N2}(g)+\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH=\mathrm{+33.2\: kJ} \label{5.4.17} \]

   Cuando se forman _{2 moles de NO 2} (el doble), el Δ H será el doble de grande:\[\ce{N2}(g)+\ce{2O2}(g)⟶\ce{2NO2}(g)\hspace{20px}ΔH=\mathrm{+66.4\: kJ} \label{5.4.18} \]

   En general, si multiplicamos o dividimos una ecuación por un número, entonces el cambio de entalpía también debería multiplicarse o dividirse por el mismo número.

2. Δ H para una reacción en una dirección es igual en magnitud y opuesto en signo a Δ H para la reacción en la dirección inversa. Por ejemplo, dado que:\[\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH=\mathrm{−184.6\:kJ} \label{5.4.19} \]

   Entonces, para la reacción “inversa”, el cambio de entalpía también se “invierte”:\[\ce{2HCl}(g)⟶\ce{H2}(g)+\ce{Cl2}(g)\hspace{20px}ΔH=\mathrm{+184.6\: kJ} \label{5.4.20} \]

Ejemplo\(\PageIndex{6}\): Stepwise Calculation of \(ΔH^\circ_\ce{f}\)

Usando la Ley de Hess Determinar la entalpía de formación,\(ΔH^\circ_\ce{f}\), de FeCl ₃ (s) a partir de los cambios de entalpía del siguiente proceso de dos etapas que ocurre bajo condiciones estatales estándar:

\[\ce{Fe}(s)+\ce{Cl2}(g)⟶\ce{FeCl2}(s)\hspace{20px}ΔH°=\mathrm{−341.8\:kJ} \nonumber \]

\[\ce{FeCl2}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH°=\mathrm \nonumber{−57.7\:kJ} \nonumber \]

Solución

Estamos tratando de encontrar la entalpía estándar de formación de FeCl3 (s), que es igual a ΔH° para la reacción:

\[\ce{Fe}(s)+\frac{3}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH^\circ_\ce{f}=\:? \nonumber \]

Al observar las reacciones, vemos que la reacción para la que queremos encontrar Δ H° es la suma de las dos reacciones con valores conocidos de Δ H, por lo que debemos sumar sus Δ H s:

\[\ce{Fe}(s)+\ce{Cl2}(g)⟶\ce{FeCl2}(s)\hspace{59px}ΔH°=\mathrm{−341.8\:kJ}\\ \underline{\ce{FeCl2}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH°=\mathrm{−57.7\:kJ}}\\ \ce{Fe}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{43px}ΔH°=\mathrm{−399.5\:kJ} \nonumber \]

La entalpía de formación,\(ΔH^\circ_\ce{f}\), de FeCl ₃ (s) es −399.5 kJ/mol.

Ejercicio\(\PageIndex{6}\)

Calcular ΔH para el proceso:

\[\ce{N2}(g)+\ce{2O2}(g)⟶\ce{2NO2}(g) \nonumber \]

a partir de la siguiente información:

\[\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g)\hspace{20px}ΔH=\mathrm{180.5\:kJ} \nonumber \]

\[\ce{NO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH=\mathrm{−57.06\:kJ} \nonumber \]

Responder

66.4 kJ

Aquí hay un ejemplo menos directo que ilustra el proceso de pensamiento involucrado en la solución de muchos problemas legales de Hess. Muestra cómo podemos encontrar muchas entalpías estándar de formación (y otros valores de Δ H) si son difíciles de determinar experimentalmente.

Ejemplo\(\PageIndex{7}\): A More Challenging Problem

Usando la Ley de Hess, el monofluoruro de cloro puede reaccionar con flúor para formar trifluoruro de cloro:

i)\(\ce{ClF}(g)+\ce{F2}(g)⟶\ce{ClF3}(g)\hspace{20px}ΔH°=\:?\)

Utilice las reacciones aquí para determinar el ΔH° para la reacción (i):

ii)\(\ce{2OF2}(g)⟶\ce{O2}(g)+\ce{2F2}(g)\hspace{20px}ΔH^\circ_{(ii)}=\mathrm{−49.4\:kJ}\)

iii)\(\ce{2ClF}(g)+\ce{O2}(g)⟶\ce{Cl2O}(g)+\ce{OF2}(g)\hspace{20px}ΔH^\circ_{(iii)}=\mathrm{+205.6\: kJ}\)

iv)\(\ce{ClF3}(g)+\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\dfrac{3}{2}\ce{OF2}(g)\hspace{20px}ΔH^\circ_{(iv)}=\mathrm{+266.7\: kJ}\)

Solución

Nuestro objetivo es manipular y combinar las reacciones (ii), (iii) y (iv) de tal manera que sumen a la reacción (i). Pasando de izquierda a derecha en (i), primero vemos que\(\ce{ClF}_{(g)}\) se necesita como reactivo. Esto se puede obtener multiplicando la reacción (iii) por\(\frac{1}{2}\), lo que significa que el cambio ΔH° también se multiplica por\(\frac{1}{2}\):

\[\ce{ClF}(g)+\frac{1}{2}\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\frac{1}{2}\ce{OF2}(g)\hspace{20px} ΔH°=\frac{1}{2}(205.6)=+102.8\: \ce{kJ} \nonumber \]

A continuación, vemos que también\(\ce{F_2}\) se necesita como reactivo. Para obtener esto, revertir y reducir a la mitad la reacción (ii), lo que significa que el ΔH° cambia de signo y se reduce a la mitad:

\[\frac{1}{2}\ce{O2}(g)+\ce{F2}(g)⟶\ce{OF2}(g)\hspace{20px}ΔH°=+24.7\: \ce{kJ} \nonumber \]

Para obtener ClF ₃ como producto, invertir (iv), cambiando el signo de ΔH°:

\[\frac{1}{2}\ce{Cl2O}(g)+\dfrac{3}{2}\ce{OF2}(g)⟶\ce{ClF3}(g)+\ce{O2}(g)\hspace{20px}ΔH°=\mathrm{−266.7\: kJ} \nonumber \]

Ahora verifique para asegurarse de que estas reacciones se sumen a la reacción que queremos:

\ [\ begin {alinear*}
&\ ce {CLf} (g) +\ frac {1} {2}\ ce {O2} (g) ⟶\ frac {1} {2}\ ce {Cl2O} (g) +\ frac {1} {2}\ ce {OF2} (g) &&ΔH°=\ mathrm {+102.8\: kJ}\
&\ frac {1} {2}\ ce {O2} (g) +\ ce {F2} (g) ⟶\ ce {OF2} (g) &&ΔH°=\ mathrm {+24.7\: kJ}\\
&\ frac {1} {2}\ ce {Cl2O} (g) +\ dfrac {3} {2}\ ce {OF2} (g) ⟶\ ce {CLF3} (g) +\ ce {O2} (g) &&ΔH°=\ mathrm {−266.7\ :kJ}\\
&\ overline {\ ce {CLF} (g) +\ ce {F2} ⟶\ ce {CLF3} (g)\ hspace {130px}} &&\ overline {ΔHH°=\ mathrm {−139.2\ :kJ}}
\ end {align*}\ nonumber\]

Reactivos\(\frac{1}{2}\ce{O2}\) y\(\frac{1}{2}\ce{O2}\) cancelar el producto O ₂; el producto\(\frac{1}{2}\ce{Cl2O}\) cancela el reactivo\(\frac{1}{2}\ce{Cl2O}\); y el reactivo\(\dfrac{3}{2}\ce{OF2}\) es cancelado por productos\(\frac{1}{2}\ce{OF2}\) y DE ₂. Esto deja solo los reactivos ClF (g) y F ₂ (g) y el producto ClF ₃ (g), que son lo que queremos. Dado que la suma de estas tres reacciones modificadas produce la reacción de interés, sumando los tres valores de ΔH° modificados dará el ΔH° deseado:

\(ΔH°=\mathrm{(+102.8\:kJ)+(24.7\:kJ)+(−266.7\:kJ)=−139.2\:kJ}\)

Ejercicio\(\PageIndex{7}\)

El cloruro de aluminio se puede formar a partir de sus elementos:

i)\(\ce{2Al}(s)+\ce{3Cl2}(g)⟶\ce{2AlCl3}(s)\hspace{20px}ΔH°=\:?\)

Utilice las reacciones aquí para determinar el ΔH° para la reacción (i):

ii)\(\ce{HCl}(g)⟶\ce{HCl}(aq)\hspace{20px}ΔH^\circ_{(ii)}=\mathrm{−74.8\:kJ}\)

iii)\(\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH^\circ_{(iii)}=\mathrm{−185\:kJ}\)

iv)\(\ce{AlCl3}(aq)⟶\ce{AlCl3}(s)\hspace{20px}ΔH^\circ_{(iv)}=\mathrm{+323\:kJ/mol}\)

(v)\(\ce{2Al}(s)+\ce{6HCl}(aq)⟶\ce{2AlCl3}(aq)+\ce{3H2}(g)\hspace{20px}ΔH^\circ_{(v)}=\mathrm{−1049\:kJ}\)

Responder

−1407 kJ

También podemos usar la ley de Hess para determinar el cambio de entalpía de cualquier reacción si se dispone de las correspondientes entalpías de formación de los reactivos y productos. Las reacciones escalonadas que consideramos son: (i) descomposiciones de los reactivos en sus elementos componentes (para lo cual los cambios de entalpía son proporcionales al negativo de las entalpías de formación de los reactivos), seguidas de (ii) recombinaciones de los elementos para dar los productos (con la entalpía cambios proporcionales a las entalpías de formación de los productos). Por lo tanto, el cambio de entalpía estándar de la reacción global es igual a: (ii) la suma de las entalpías estándar de formación de todos los productos más (i) la suma de los negativos de las entalpías estándar de formación de los reactivos. Esto generalmente se reordena ligeramente para escribirse de la siguiente manera,\(\sum\) representando “la suma de” y n representando los coeficientes estequiométricos:

\[ΔH^\circ_\ce{reaction}=\sum n×ΔH^\circ_\ce{f}\ce{(products)}−\sum n×ΔH^\circ_\ce{f}\ce{(reactants)} \label{5.4.20B} \]

El siguiente ejemplo muestra en detalle por qué esta ecuación es válida, y cómo usarla para calcular el cambio de entalpía para una reacción de interés.

Ejemplo\(\PageIndex{8}\): Using Hess’s Law

Cuál es el cambio de entalpía estándar para la reacción:

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g)\hspace{20px}ΔH°=\:? \nonumber \]

Solución 1: Usando la Ecuación

Alternativamente, podríamos usar la forma especial de la ley de Hess dada anteriormente:

\[ΔH^\circ_\ce{reaction}=∑n×ΔH^\circ_\ce{f}\ce{(products)}−∑n×ΔH^\circ_\ce{f}\ce{(reactants)} \nonumber \]

\[\begin {align*} &=\mathrm{\left[2\:\cancel{mol\:HNO_3}×\dfrac{−207.4\:kJ}{\cancel{mol\:HNO_3\:(\mathit{aq})}}+1\:\cancel{mol\: NO\:(\mathit{g})}×\dfrac{+90.2\: kJ}{\cancel{mol\: NO\:(\mathit{g})}}\right]}\\ &\mathrm{\:−\,\left[3\:\cancel{mol\:NO_2(\mathit{g})}×\dfrac{+33.2\: kJ}{\cancel{mol\:NO_2\:(\mathit{g})}}+1\:\cancel{mol\:H_2O\:(\mathit{l})}×\dfrac{−285.8\:kJ}{\cancel{mol\:H_2O\:(\mathit{l})}}\right]}\\ &=\mathrm{2(−207.4\:kJ)+1(+90.2\: kJ)−3(+33.2\: kJ)−1(−285.8\:kJ)}\\ &=\mathrm{−138.4\:kJ}\end {align*} \nonumber \]

S olution 2: Apoyando por qué la ecuación general es válida

Podemos escribir esta reacción como la suma de las descomposiciones de 3NO ₂ (g) y 1H ₂ O (l) en sus elementos constituyentes, y la formación de 2 HNO ₃ (aq) y 1 NO (g) a partir de sus elementos constituyentes. Escribiendo estas reacciones, y señalando sus relaciones con los\(ΔH^\circ_\ce{f}\) valores de estos compuestos (de las Tablas T1 y T2), tenemos:

\[\ce{3NO2}(g)⟶ \dfrac{3}{2} \ce{N2}(g)+ 3 \ce{O2}(g)\hspace{20px}ΔH^\circ_{1}=\mathrm{−99.6\:kJ} \nonumber \]

\[\ce{H2O}(l)⟶\ce{H2}(g)+\frac{1}{2}\ce{O2}(g)\hspace{20px}ΔH^\circ_{2}=+285.8\: \ce{kJ}\:[−1×ΔH^\circ_\ce{f}(\ce{H2O})] \nonumber \]

\[\ce{H2}(g)+\ce{N2}(g)+ 3 \ce{O2}(g)⟶\ce{2HNO3}(aq)\hspace{20px}ΔH^\circ_{3}=−414.8\:kJ\:[2×ΔH^\circ_\ce{f}(\ce{HNO3 \nonumber})] \nonumber \]

\[\frac{1}{2}\ce{N2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{NO}(g)\hspace{20px}ΔH^\circ \nonumber_{4}=+90.2\: \ce{kJ}\:[1×(\ce{NO})] \nonumber \]

Sumando estas ecuaciones de reacción da la reacción que nos interesa:

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g) \nonumber \]

Sumando sus cambios de entalpía da el valor que queremos determinar:

\[\begin {align*} ΔH^\circ_\ce{rxn}&=ΔH^\circ_1+ΔH^\circ_2+ΔH^\circ_3+ΔH^\circ_4=\mathrm{(−99.6\:kJ)+(+285.8\: kJ)+(−414.8\:kJ)+(+90.2\: kJ)}\\ &=\mathrm{−138.4\:kJ} \end {align*} \nonumber \]

Entonces el cambio de entalpía estándar para esta reacción es Δ H° = −138.4 kJ.

Obsérvese que este resultado fue obtenido por:

1. multiplicando el\(ΔH^\circ_\ce{f}\) de cada producto por su coeficiente estequiométrico y sumando esos valores,
2. multiplicando el\(ΔH^\circ_\ce{f}\) de cada reactivo por su coeficiente estequiométrico y sumando esos valores, y luego
3. restando el resultado encontrado en el paso 2 del resultado encontrado en el paso 1.

Este es también el procedimiento en el uso de la ecuación general, como se muestra.

Ejercicio\(\PageIndex{8}\)

Calcular el calor de combustión de 1 mol de etanol, C ₂ H ₅ OH (l), cuando se forman H ₂ O (l) y CO ₂ (g). Utilice las siguientes entalpías de formación: C ₂ H ₅ OH (l), −278 kJ/mol; H ₂ O (l), −286 kJ/mol; y CO ₂ (g), −394 kJ/mol.

Responder

−1368 kJ/mol

Resumen

Si se lleva a cabo un cambio químico a presión constante y el único trabajo realizado es causado por expansión o contracción, q para el cambio se denomina cambio de entalpía con el símbolo Δ H, o\(ΔH^\circ_{298}\) para reacciones que ocurren bajo condiciones de estado estándar. El valor de Δ H para una reacción en una dirección es igual en magnitud, pero de signo opuesto, a Δ H para la reacción en la dirección opuesta, y Δ H es directamente proporcional a la cantidad de reactivos y productos. Ejemplos de cambios en la entalpía incluyen entalpía de combustión, entalpía de fusión, entalpía de vaporización y entalpía estándar de formación. La entalpía estándar de formación,\(ΔH^\circ_\ce{f}\), es el cambio de entalpía que acompaña a la formación de 1 mol de una sustancia a partir de los elementos en sus estados más estables a 1 bar (estado estándar). Muchos de los procesos se llevan a cabo a 298.15 K. Si las entalpías de formación están disponibles para los reactivos y productos de una reacción, el cambio de entalpía se puede calcular usando la ley de Hess: Si un proceso puede escribirse como la suma de varios procesos paso a paso, el cambio de entalpía del proceso total es igual a la suma de los cambios de entalpía de los distintos pasos.

Ecuaciones Clave

• \(ΔU=q+w\)
• \(ΔH^\circ_\ce{reaction}=∑n×ΔH^\circ_\ce{f}\ce{(products)}−∑n×ΔH^\circ_\ce{f}\ce{(reactants)}\)

Notas al pie

1. 1 Para más información sobre el combustible de algas, consulte www.theguardian.com/vironme... n-fuel-problem.

Glosario

termodinámica química

área de la ciencia que se ocupa de las relaciones entre el calor, el trabajo y todas las formas de energía asociadas a los procesos químicos y físicos

entalpía (H)

suma de la energía interna de un sistema y el producto matemático de su presión y volumen

Cambio de entalpía (Δ H)

calor liberado o absorbido por un sistema bajo presión constante durante un proceso químico o físico

trabajo de expansión (trabajo presión-volumen)

trabajo realizado como un sistema se expande o contrae contra la presión externa

primera ley de la termodinámica

la energía interna de un sistema cambia debido al flujo de calor dentro o fuera del sistema o al trabajo realizado en o por el sistema

Ley de Hess

si un proceso puede representarse como la suma de varios pasos, el cambio de entalpía del proceso es igual a la suma de los cambios de entalpía de los pasos

hidrocarburo

compuesto solo de hidrógeno y carbono; el componente principal de los combustibles fósiles

energía interna (U)

total de todos los tipos posibles de energía presentes en una sustancia o sustancias

entalpía estándar de combustión (\(ΔH^\circ_\ce{c}\))

calor liberado cuando un mol de un compuesto se somete a combustión completa en condiciones estándar

entalpía estándar de formación (\(ΔH^\circ_\ce{f}\))

Cambio de entalpía de una reacción química en la que se forma 1 mol de una sustancia pura a partir de sus elementos en sus estados más estables bajo condiciones de estado estándar

estado estándar

conjunto de condiciones físicas aceptadas como condiciones de referencia comunes para reportar propiedades termodinámicas; 1 bar de presión, y soluciones a concentraciones 1 molar, generalmente a una temperatura de 298.15 K

función de estado

propiedad dependiendo únicamente del estado de un sistema, y no del camino tomado para llegar a ese estado