9.1: Presión de gas
- Page ID
- 75826
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Definir la propiedad de la presión
- Definir y convertir entre las unidades de medición de presión
- Describir el funcionamiento de herramientas comunes para medir la presión de gas
- Calcular presión a partir de datos del manómetro
La atmósfera terrestre ejerce una presión, al igual que cualquier otro gas. Aunque normalmente no notamos la presión atmosférica, somos sensibles a los cambios de presión, por ejemplo, cuando tus oídos “estallan” durante el despegue y aterrizaje mientras vuela, o cuando buceas bajo el agua. La presión del gas es causada por la fuerza ejercida por las moléculas de gas que chocan con las superficies de los objetos (Figura\(\PageIndex{1}\)). Aunque la fuerza de cada colisión es muy pequeña, cualquier superficie de área apreciable experimenta una gran cantidad de colisiones en poco tiempo, lo que puede resultar en una alta presión. De hecho, la presión de aire normal es lo suficientemente fuerte como para aplastar un contenedor de metal cuando no se equilibra con la misma presión desde el interior del contenedor.
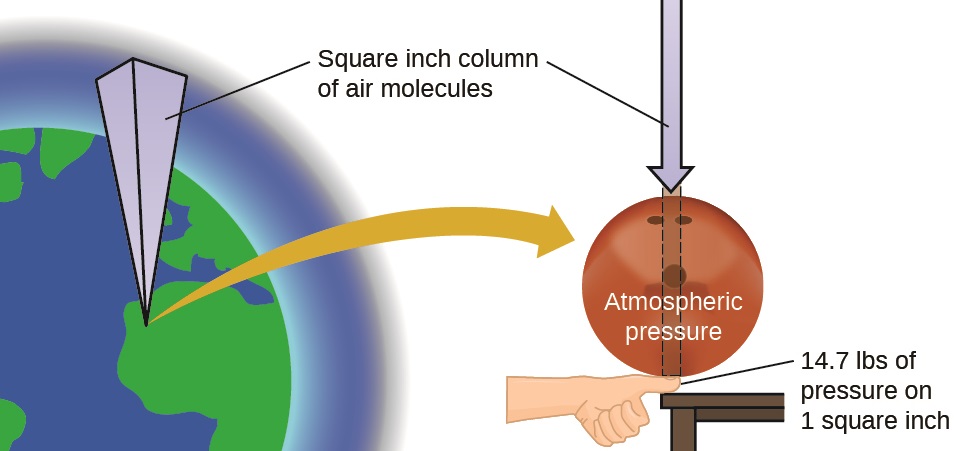
La presión atmosférica es causada por el peso de la columna de moléculas de aire en la atmósfera sobre un objeto, como el carro cisterna. A nivel del mar, esta presión es aproximadamente la misma que la que ejerce un elefante africano adulto parado sobre un felpudo, o una bola de boliche típica que descansa sobre tu miniatura. Estas pueden parecer enormes cantidades, y lo son, pero la vida en la tierra ha evolucionado bajo tal presión atmosférica. Si realmente colocas una bola de boliche en tu miniatura, la presión experimentada es el doble de la presión habitual, y la sensación es desagradable.

En este breve video se ofrece una ilustración dramática de la presión atmosférica, que muestra un vagón cisterna de ferrocarril implosionando cuando disminuye su presión interna.
La presión se define como la fuerza ejercida sobre un área dada:
\[P=\dfrac{F}{A} \label{9.2.1} \]
Dado que la presión es directamente proporcional a la fuerza e inversamente proporcional al área (Ecuación\ ref {9.2.1}), la presión puede aumentarse ya sea aumentando la cantidad de fuerza o disminuyendo el área sobre la que se aplica. Correspondientemente, la presión se puede disminuir ya sea disminuyendo la fuerza o aumentando el área.
Apliquemos la definición de presión (Ecuación\ ref {9.2.1}) para determinar cuál sería más probable que caiga a través del hielo fino en la Figura\(\PageIndex{2}\). ¿el elefante o el patinador artístico?

Un elefante africano grande puede pesar 7 toneladas, apoyado en cuatro pies, cada uno con un diámetro de aproximadamente 1.5 pies (área de huella de 250 en 2), por lo que la presión ejercida por cada pie es de aproximadamente 14 lb/in 2:
\[\mathrm{pressure\: per\: elephant\: foot=14,000\dfrac{lb}{elephant}×\dfrac{1\: elephant}{4\: feet}×\dfrac{1\: foot}{250\:in^2}=14\:lb/in^2} \label{9.2.2} \]
El patinador artístico pesa alrededor de 120 lbs, soportado sobre dos cuchillas para patines, cada una con un área de aproximadamente 2 en 2, por lo que la presión ejercida por cada cuchilla es de aproximadamente 30 lb/in 2:
\[\mathrm{pressure\: per\: skate\: blade=120\dfrac{lb}{skater}×\dfrac{1\: skater}{2\: blades}×\dfrac{1\: blade}{2\:in^2}=30\:lb/in^2} \label{9.2.3} \]
A pesar de que el elefante es más de cien veces más pesado que el patinador, ejerce menos de la mitad de la presión y por lo tanto sería menos probable que cayera a través de hielo fino. Por otro lado, si la patinadora se quita los patines y se para con los pies descalzos (o calzado regular) sobre el hielo, la mayor área sobre la que se aplica su peso reduce en gran medida la presión ejercida:
\[\mathrm{pressure\: per\: human\: foot=120\dfrac{lb}{skater}×\dfrac{1\: skater}{2\: feet}×\dfrac{1\: foot}{30\:in^2}=2\:lb/in^2} \label{9.2.4} \]
La unidad de presión SI es el pascal (Pa), con 1 Pa = 1 N/m 2, donde N es el newton, una unidad de fuerza definida como 1 kg m/s 2. Un pascal es una presión pequeña; en muchos casos, es más conveniente usar unidades de kilopascal (1 kPa = 1000 Pa) o bar (1 bar = 100,000 Pa). En Estados Unidos, la presión a menudo se mide en libras de fuerza en un área de una pulgada cuadrada, libras por pulgada cuadrada (psi), por ejemplo, en llantas de automóviles. La presión también se puede medir utilizando la atmósfera unitaria (atm), que originalmente representaba la presión media del aire a nivel del mar en la latitud aproximada de París (45°). \(\PageIndex{1}\)La tabla proporciona información sobre estas y algunas otras unidades comunes para mediciones de presión
| Nombre y abreviatura de la unidad | Definición o relación con otra unidad | Comentar |
|---|---|---|
| pascal | 1 Pa = 1 N/m 2 | Unidad IUPAC recomendada |
| kilopascales (kPa) | 1 kPa = 1000 Pa | |
| libras por pulgada cuadrada (psi) | la presión del aire al nivel del mar es de ~14.7 psi | |
| atmósfera (atm) | 1 atm = 101,325 Pa | la presión del aire al nivel del mar es de ~1 atm |
| barra (barra, o b) | 1 bar = 100,000 Pa (exactamente) | de uso común en meteorología |
| milibar (mbar o mb) | 1000 mbar = 1 bar | |
| pulgadas de mercurio (pulg. Hg) | 1 pulg. Hg = 3386 Pa | utilizado por la industria de la aviación, también algunos informes meteorológicos |
| torr | \(\mathrm{1\: torr=\dfrac{1}{760}\:atm}\) | lleva el nombre de Evangelista Torricelli, inventor del barómetro |
| milímetros de mercurio (mm Hg) | 1 mm Hg ~1 torr |
El Servicio Meteorológico Nacional de Estados Unidos reporta presión tanto en pulgadas de Hg como en milibares. Convierta una presión de 29.2 pulg. Hg en:
- torr
- atm
- kPa
- mbar
Solución
Este es un problema de conversión de unidades. Las relaciones entre las distintas unidades de presión se dan en el Cuadro 9.2.1.
- \(\mathrm{29.2\cancel{in\: Hg}×\dfrac{25.4\cancel{mm}}{1\cancel{in}} ×\dfrac{1\: torr}{1\cancel{mm\: Hg}} =742\: torr}\)
- \(\mathrm{742\cancel{torr}×\dfrac{1\: atm}{760\cancel{torr}}=0.976\: atm}\)
- \(\mathrm{742\cancel{torr}×\dfrac{101.325\: kPa}{760\cancel{torr}}=98.9\: kPa}\)
- \(\mathrm{98.9\cancel{kPa}×\dfrac{1000\cancel{Pa}}{1\cancel{kPa}} \times \dfrac{1\cancel{bar}}{100,000\cancel{Pa}} \times\dfrac{1000\: mbar}{1\cancel{bar}}=989\: mbar}\)
Una presión barométrica típica en Kansas City es de 740 torr. ¿Cuál es esta presión en atmósferas, en milímetros de mercurio, en kilopascales y en bar?
- Contestar
-
0.974 atm; 740 mm Hg; 987 kPa; 0.987 bar
Podemos medir la presión atmosférica, la fuerza ejercida por la atmósfera sobre la superficie terrestre, con un barómetro (Figura\(\PageIndex{3}\)). Un barómetro es un tubo de vidrio que se cierra por un extremo, se llena con un líquido no volátil como el mercurio, y luego se invierte y se sumerge en un recipiente de ese líquido. La atmósfera ejerce presión sobre el líquido fuera del tubo, la columna de líquido ejerce presión dentro del tubo, y la presión en la superficie del líquido es la misma dentro y fuera del tubo. La altura del líquido en el tubo es, por lo tanto, proporcional a la presión ejercida por la atmósfera.
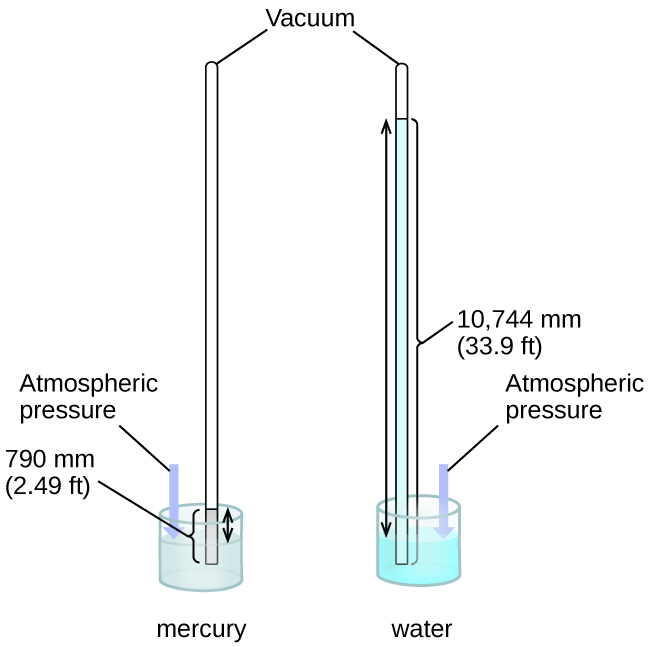
Si el líquido es agua, la presión atmosférica normal soportará una columna de agua de más de 10 metros de altura, lo cual es bastante inconveniente para hacer (y leer) un barómetro. Debido a que el mercurio (Hg) es aproximadamente 13.6 veces más denso que el agua, un barómetro de mercurio solo necesita ser\(\dfrac{1}{13.6}\) tan alto como un barómetro de agua, un tamaño más adecuado. La presión atmosférica estándar de 1 atm al nivel del mar (101,325 Pa) corresponde a una columna de mercurio que tiene aproximadamente 760 mm (29.92 pulg.) de altura. El torr originalmente estaba destinado a ser una unidad igual a un milímetro de mercurio, pero ya no corresponde exactamente. La presión ejercida por un fluido debido a la gravedad se conoce como presión hidrostática, p:
\[p=hρg \label{9.2.5} \]
donde
- \(h\)es la altura del fluido,
- \(ρ\)es la densidad del fluido, y
- \(g\)es la aceleración debido a la gravedad.
Mostrar el cálculo que sustenta la afirmación de que la presión atmosférica cerca del nivel del mar corresponde a la presión ejercida por una columna de mercurio que tiene aproximadamente 760 mm de altura. La densidad del mercurio =\(13.6 \,g/cm^3\).
Solución
La presión hidrostática viene dada por la Ecuación\ ref {9.2.5}\(h = 760 \,mm\), con\(ρ = 13.6\, g/cm^3\), y\(g = 9.81 \,m/s^2\). Conectando estos valores a la Ecuación\ ref {9.2.5} y haciendo las conversiones unitarias necesarias nos dará el valor que buscamos. (Nota: Estamos esperando encontrar una presión de ~101,325 Pa:)
\[\mathrm{101,325\:\mathit{N}/m^2=101,325\:\dfrac{kg·m/s^2}{m^2}=101,325\:\dfrac{kg}{m·s^2}} \nonumber \]
\ [\ begin {alinear*}
p&\ mathrm {=\ izquierda (760\: mm×\ dfrac {1\: m} {1000\: mm}\ derecha) ×\ izquierda (\ dfrac {13.6\: g} {1\ :cm^3} ×\ dfrac {1\: kg} {1000\: g} ×\ dfrac {(100\: cm) ^3} {(1\: m) ^3}\ derecha) ×\ izquierda (\ dfrac {9.81\: m} {1\ :s^2}\ derecha)}\\ [4pt]
&\ mathrm {=( 0.760\: m) (13.600\ :kg/m^3) (9.81\ :m/s^2) =1. 01\ times 10^5\ :kg/ms^2=1.01×10^5\ mathit {N} /m^2}\\[4pt] & \mathrm{=1.01×10^5\:Pa} \end {align*} \nonumber \]
Calcular la altura de una columna de agua a 25 °C que corresponde a la presión atmosférica normal. La densidad del agua a esta temperatura es de 1.0 g/cm 3.
- Contestar
-
10.3 m
Un manómetro es un dispositivo similar a un barómetro que se puede utilizar para medir la presión de un gas atrapado en un contenedor. Un manómetro de extremo cerrado es un tubo en forma de U con un brazo cerrado, un brazo que se conecta al gas que se va a medir y un líquido no volátil (generalmente mercurio) en el medio. Al igual que con un barómetro, la distancia entre los niveles de líquido en los dos brazos del tubo (h en el diagrama) es proporcional a la presión del gas en el contenedor. Un manómetro de extremo abierto (Figura\(\PageIndex{3}\)) es lo mismo que un manómetro de extremo cerrado, pero uno de sus brazos está abierto a la atmósfera. En este caso, la distancia entre los niveles de líquido corresponde a la diferencia de presión entre el gas en el contenedor y la atmósfera.
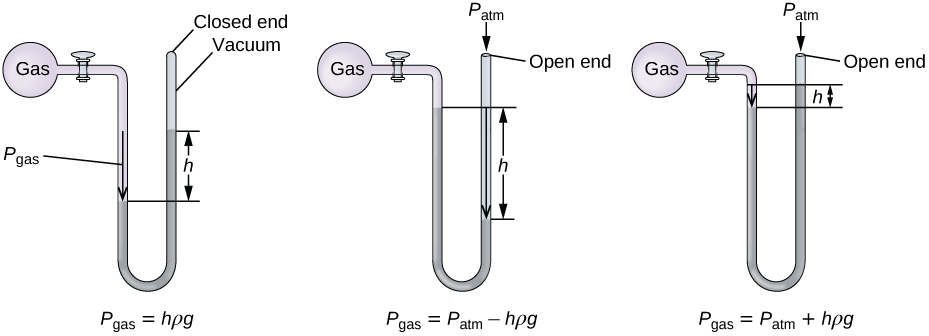
La presión de una muestra de gas se mide al nivel del mar con un manómetro de Hg (mercurio) de extremo abierto, como se muestra a continuación. Determinar la presión del gas en:
- mm Hg
- atm
- kPa
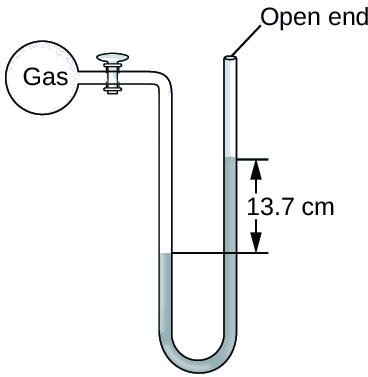
Solución
La presión del gas es igual a la presión hidrostática debido a una columna de mercurio de altura 13.7 cm más la presión de la atmósfera al nivel del mar. (La presión en la línea horizontal inferior es igual en ambos lados del tubo. La presión a la izquierda se debe al gas y la presión a la derecha se debe a 13.7 cm de Hg más presión atmosférica).
- En mm Hg, esto es: 137 mm Hg + 760 mm Hg = 897 mm Hg
- \(\mathrm{897\cancel{mm Hg}×\dfrac{1\: atm}{760\cancel{mm Hg}}=1.18\: atm}\)
- \(\mathrm{1.18\cancel{atm}×\dfrac{101.325\: kPa}{1\cancel{atm}}=1.20×10^2\:kPa}\)
La presión de una muestra de gas se mide al nivel del mar con un manómetro de Hg de extremo abierto, como se muestra a continuación Determine la presión del gas en:
- mm Hg
- atm
- kPa
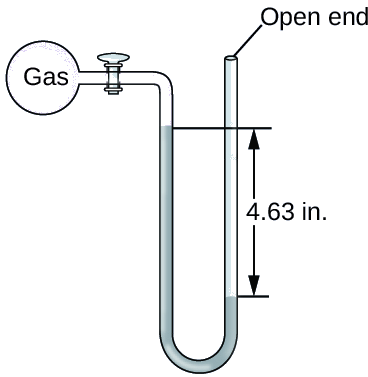
Contestar a
-
642 mm Hg
- Respuesta b
-
0.845 atm
- Respuesta c
-
85.6 kPa
La presión arterial se mide mediante un dispositivo llamado esfigmomanómetro (esfigmos griego = “pulso”). Consiste en un manguito inflable para restringir el flujo sanguíneo, un manómetro para medir la presión, y un método para determinar cuándo comienza el flujo sanguíneo y cuándo se ve obstaculizado (Figura\(\PageIndex{5}\)). Desde su invención en 1881, ha sido un dispositivo médico esencial. Existen muchos tipos de esfigmomanómetros: los manuales que requieren un estetoscopio y son utilizados por profesionales médicos; los de mercurio, utilizados cuando se requiere la mayor precisión; los mecánicos menos precisos; y los digitales que se pueden usar con poco entrenamiento pero que tienen limitaciones. Al usar un esfigmomanómetro, el manguito se coloca alrededor de la parte superior del brazo y se infla hasta que el flujo sanguíneo se bloquea por completo, luego se libera lentamente. A medida que late el corazón, la sangre forzada a través de las arterias provoca un aumento de la presión. Este aumento de la presión a la que comienza el flujo sanguíneo es la presión sistólica, la presión máxima en el ciclo cardíaco. Cuando la presión del manguito es igual a la presión sistólica arterial, la sangre fluye más allá del manguito, creando sonidos audibles que se pueden escuchar usando un estetoscopio. A esto le sigue una disminución de la presión a medida que los ventrículos del corazón se preparan para otro latido. A medida que la presión del manguito continúa disminuyendo, eventualmente el sonido ya no se escucha; esta es la presión diastólica, la presión más baja (fase de reposo) en el ciclo cardíaco. Las unidades de presión arterial de un esfigmomanómetro son en términos de milímetros de mercurio (mm Hg).

Meteorología, Climatología y Ciencias Atmosféricas
A lo largo de los siglos, la gente ha observado nubes, vientos y precipitaciones, tratando de discernir patrones y hacer predicciones: cuándo es mejor plantar y cosechar; si es seguro emprender un viaje por mar; y mucho más. Ahora enfrentamos complejos desafíos relacionados con el clima y la atmósfera que tendrán un gran impacto en nuestra civilización y el ecosistema. Varias disciplinas científicas diferentes utilizan principios químicos para ayudarnos a comprender mejor el clima, la atmósfera y el clima. Estas son la meteorología, la climatología y la ciencia atmosférica. La meteorología es el estudio de la atmósfera, los fenómenos atmosféricos y los efectos atmosféricos sobre el clima terrestre. Los meteorólogos buscan comprender y predecir el clima a corto plazo, lo que puede salvar vidas y beneficiar a la economía. Los pronósticos meteorológicos (Figura\(\PageIndex{5}\)) son el resultado de miles de mediciones de presión del aire, temperatura y similares, que se compilan, modelan y analizan en centros meteorológicos de todo el mundo.
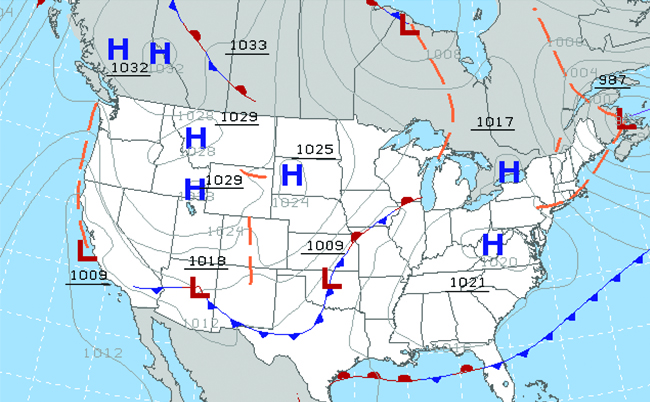
En términos de clima, los sistemas de baja presión ocurren cuando la presión atmosférica de la superficie terrestre es menor que el ambiente circundante: El aire húmedo se eleva y se condensa, produciendo nubes. El movimiento de humedad y aire dentro de varios frentes meteorológicos instiga la mayoría de los eventos climáticos
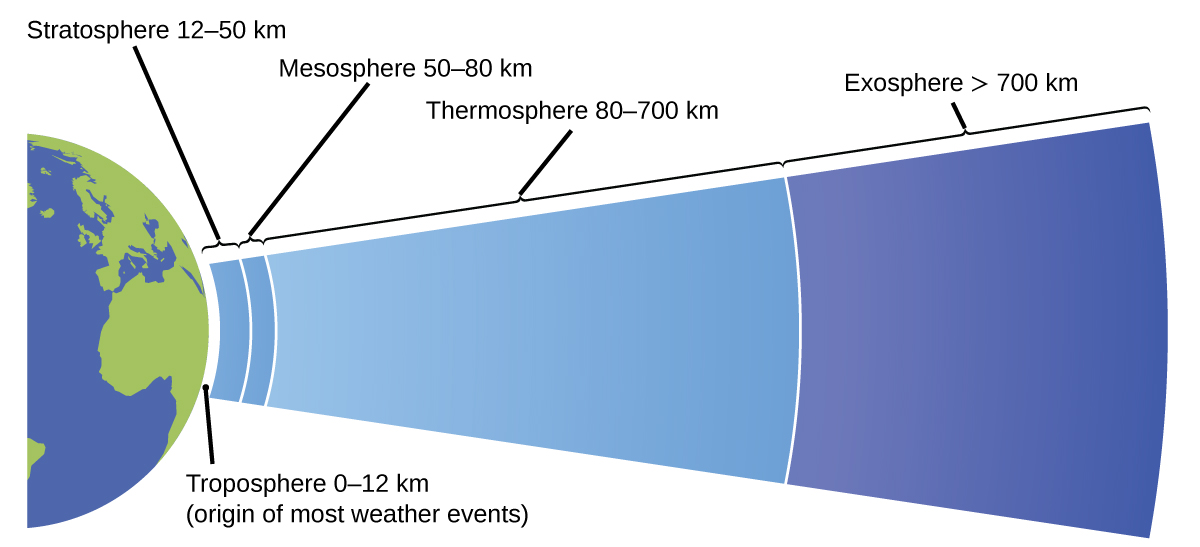
La atmósfera es la capa gaseosa que rodea a un planeta. La atmósfera terrestre, que tiene aproximadamente 100—125 km de espesor, consiste en aproximadamente 78.1% de nitrógeno y 21.0% de oxígeno, y puede subdividirse aún más en las regiones que se muestran en la Figura\(\PageIndex{7}\): la exosfera (más alejada de la tierra, > 700 km sobre el nivel del mar), la termosfera (80-700 km), la mesosfera (50—80 km), la estratosfera (segundo nivel más bajo de nuestra atmósfera, 12—50 km sobre el nivel del mar), y la troposfera (hasta 12 km sobre el nivel del mar, aproximadamente el 80% de la atmósfera terrestre por masa y la capa donde se originan la mayoría de los eventos climáticos). A medida que vas más alto en la troposfera, tanto la densidad del aire como la temperatura disminuyen.
La climatología es el estudio del clima, promediando las condiciones climáticas durante largos periodos de tiempo, utilizando datos atmosféricos. Sin embargo, los climatólogos estudian patrones y efectos que ocurren a lo largo de décadas, siglos y milenios, en lugar de marcos de tiempo más cortos de horas, días y semanas como los meteorólogos. La ciencia atmosférica es un campo aún más amplio, que combina meteorología, climatología y otras disciplinas científicas que estudian la atmósfera.
Resumen
Los gases ejercen presión, que es fuerza por unidad de área. La presión de un gas puede expresarse en la unidad SI de pascal o kilopascal, así como en muchas otras unidades incluyendo torr, atmósfera y bar. La presión atmosférica se mide usando un barómetro; otras presiones de gas se pueden medir usando uno de varios tipos de manómetros.
Ecuaciones Clave
- \(P=\dfrac{F}{A}\)
- p = hρg
Glosario
- atmósfera (atm)
- unidad de presión; 1 atm = 101,325 Pa
- bar
- (bar o b) unidad de presión; 1 bar = 100,000 Pa
- barómetro
- dispositivo utilizado para medir la presión atmosférica
- presión hidrostática
- presión ejercida por un fluido debido a la gravedad
- manómetro
- dispositivo utilizado para medir la presión de un gas atrapado en un contenedor
- pascal
- Unidad de presión SI; 1 Pa = 1 N/m 2
- libras por pulgada cuadrada (psi)
- unidad de presión común en Estados Unidos
- presión
- fuerza ejercida por unidad de área
- torr
- unidad de presión;\(\mathrm{1\: torr=\dfrac{1}{760}\,atm}\)


