16.1: Espontaneidad
- Page ID
- 75148
- Distinguir entre procesos espontáneos y no espontáneos
- Describir la dispersión de materia y energía que acompaña a ciertos procesos espontáneos
En esta sección, considere las diferencias entre dos tipos de cambios en un sistema: Los que ocurren espontáneamente y los que ocurren sólo con la entrada continua de energía. Al hacerlo, obtendremos una comprensión de por qué algunos sistemas están naturalmente inclinados a cambiar en una dirección bajo ciertas condiciones. También obtendremos una idea de cómo la espontaneidad de un proceso afecta la distribución de energía y materia dentro del sistema.
Procesos espontáneos y no espontáneos
Los procesos tienen una tendencia natural a ocurrir en una dirección bajo un conjunto dado de condiciones. El agua fluirá naturalmente cuesta abajo, pero el flujo cuesta arriba requiere una intervención externa como el uso de una bomba. Un proceso espontáneo es aquel que ocurre naturalmente bajo ciertas condiciones. Un proceso no espontáneo, por otro lado, no se llevará a cabo a menos que sea “impulsado” por la entrada continua de energía de una fuente externa. Un proceso que es espontáneo en una dirección bajo un conjunto particular de condiciones no es espontáneo en la dirección inversa. A temperatura ambiente y presión atmosférica típica, por ejemplo, el hielo se derretirá espontáneamente, pero el agua no se congelará espontáneamente.
La espontaneidad de un proceso no se correlaciona con la velocidad del proceso. Un cambio espontáneo puede ser tan rápido que es esencialmente instantáneo o tan lento que no se puede observar en ningún período práctico de tiempo. Para ilustrar este concepto, considere la desintegración de los isótopos radiactivos, un tema tratado más a fondo en el capítulo sobre química nuclear. La desintegración radiactiva es por definición un proceso espontáneo en el que los núcleos de los isótopos inestables emiten radiación a medida que se convierten en núcleos más estables. Todos los procesos de descomposición ocurren espontáneamente, pero las tasas a las que los diferentes isótopos se descomponen varían ampliamente. El tecnecio-99m es un radioisótopo popular para estudios de imágenes médicas que experimenta una descomposición relativamente rápida y exhibe una vida media de aproximadamente seis horas. El uranio-238 es el isótopo más abundante del uranio, y su desintegración ocurre mucho más lentamente, exhibiendo una vida media de más de cuatro mil millones de años (Figura\(\PageIndex{1}\)).
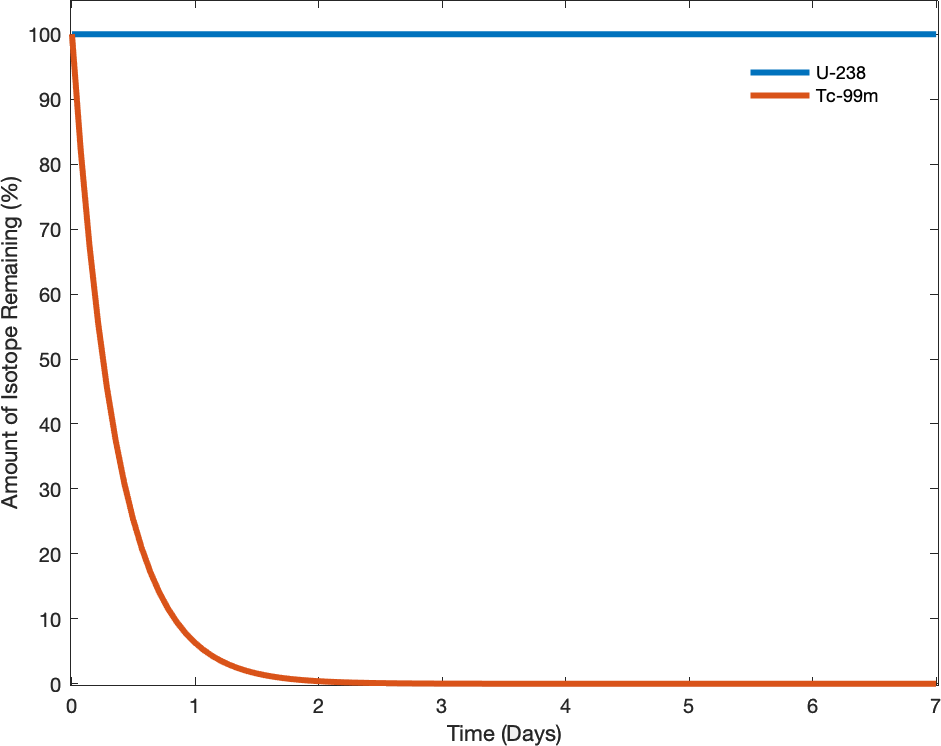
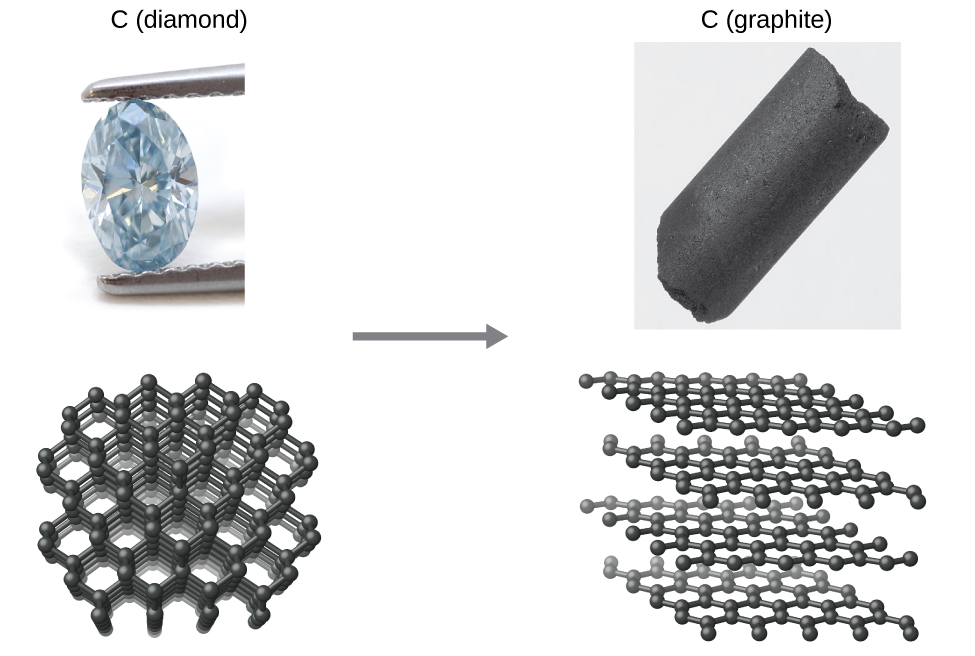
Como otro ejemplo, considere la conversión del diamante en grafito (Figura\(\PageIndex{2}\)).
\[\ce{C(s, diamond)}⟶\ce{C(s, graphite)} \label{Eq1} \]
El diagrama de fases para el carbono indica que el grafito es la forma estable de este elemento bajo presión atmosférica ambiente, mientras que el diamante es el alótropo estable a presiones muy altas, como las presentes durante su formación geológica. Los cálculos termodinámicos del tipo descrito en la última sección de este capítulo indican que la conversión del diamante en grafito a presión ambiente ocurre espontáneamente, sin embargo, se observa que los diamantes existen, y persisten, bajo estas condiciones. Aunque el proceso es espontáneo en condiciones ambientales típicas, su velocidad es extremadamente lenta, por lo que para todos los fines prácticos los diamantes son de hecho “para siempre”. Situaciones como estas enfatizan la importante distinción entre los aspectos termodinámicos y cinéticos de un proceso. En este caso particular, se dice que los diamantes son termodinámicamente inestables pero cinéticamente estables en condiciones ambientales.
Dispersión de Materia y Energía
A medida que extendemos nuestra discusión de conceptos termodinámicos hacia el objetivo de predecir la espontaneidad, consideramos ahora un sistema aislado que consiste en dos matraces conectados con una válvula cerrada. Inicialmente hay un gas ideal a la izquierda y un vacío a la derecha (Figura\(\PageIndex{3}\)). Cuando se abre la válvula, el gas se expande espontáneamente para llenar ambos matraces. Al recordar la definición de trabajo presión-volumen del capítulo sobre termoquímica, tenga en cuenta que no se ha realizado ningún trabajo porque la presión en un vacío es cero.
\[ \begin{align} w&=−PΔV \\[4pt]&=0 \,\,\, \mathrm{(P=0\: in\: a\: vaccum)} \label{Eq2} \end{align} \]
Obsérvese también que dado que el sistema está aislado, no se ha intercambiado calor con los alrededores (q = 0). La primera ley de la termodinámica confirma que no ha habido ningún cambio en la energía interna del sistema como resultado de este proceso.
\[ \begin{align} ΔU&=q+w \tag{First Law of Thermodynamics} \\[4pt] &=0+0=0 \label{Eq3}\end{align} \]
Por lo tanto, la espontaneidad de este proceso no es consecuencia de ningún cambio de energía que acompañe al proceso. En cambio, el movimiento del gas parece estar relacionado con la dispersión mayor y más uniforme de la materia que resulta cuando se permite que el gas se expanda. Inicialmente, el sistema estaba compuesto por un matraz que contenía materia y otro matraz que no contenía nada. Después del proceso espontáneo, la materia se distribuyó tanto de manera más amplia (ocupando el doble de su volumen original) como de manera más uniforme (presente en cantidades iguales en cada matraz).
Consideremos ahora dos objetos a diferentes temperaturas: el objeto X a la temperatura T X y el objeto Y a la temperatura T Y, con T X > T Y (Figura\(\PageIndex{4}\)). Cuando estos objetos entran en contacto, el calor fluye espontáneamente del objeto más caliente (X) al más frío (Y). Esto corresponde a una pérdida de energía térmica por X y una ganancia de energía térmica por Y.
\[q_\ce{X}<0 \hspace{20px} \ce{and} \hspace{20px} q_\ce{Y}=−q_\ce{X}>0 \label{Eq4} \]
Desde la perspectiva de este sistema de dos objetos, no hubo ganancia neta ni pérdida de energía térmica, sino que la energía térmica disponible se redistribuyó entre los dos objetos. Este proceso espontáneo resultó en una dispersión más uniforme de la energía.
Como lo ilustran los dos procesos descritos, un factor importante para determinar la espontaneidad de un proceso es la medida en que cambia la dispersión o distribución de materia y/o energía. En cada caso, se produjo un proceso espontáneo que resultó en una distribución más uniforme de la materia o energía.
Describir cómo se redistribuyen la materia y la energía cuando ocurren los siguientes procesos espontáneos:
- Un sólido sublima.
- Un gas se condensa.
- Una gota de colorante alimentario añadida a un vaso de agua forma una solución con color uniforme.
Solución
- La sublimación es la conversión de un sólido (densidad relativamente alta) en un gas (densidad mucho menor). Este proceso produce una dispersión mucho mayor de la materia, ya que las moléculas ocuparán un volumen mucho mayor después de la transición sólido-gas. Sin embargo, se requirió una entrada de energía de los alrededores para que las moléculas abandonaran la fase sólida y entraran en la fase gaseosa.
- La condensación es la conversión de un gas (densidad relativamente baja) a un líquido (densidad mucho mayor). Este proceso produce una dispersión mucho menor de la materia, ya que las moléculas ocuparán un volumen mucho menor después de la transición gas a líquido. A medida que las moléculas de gas se mueven juntas para formar las gotitas de líquido, forman fuerzas intermoleculares y así liberan energía al entorno.
- El proceso en cuestión es la dilución. Las moléculas de colorante alimentario inicialmente ocupan un volumen mucho menor (la gota de solución de tinte) de lo que ocupan una vez que se completa el proceso (en el vaso lleno de agua). Por lo tanto, el proceso conlleva una mayor dispersión de la materia. El proceso también puede producir una dispersión más uniforme de la materia, ya que el estado inicial del sistema involucra dos regiones de diferentes concentraciones de colorante (alta en la caída, cero en el agua), y el estado final del sistema contiene una sola concentración de colorante en todo el proceso. Este proceso puede ocurrir sin un cambio de energía debido a que las moléculas tienen energía cinética relativa a la temperatura del agua, y así estarán en constante movimiento.
Describa cómo se redistribuyen la materia y la energía cuando vacía un bote de aire comprimido en una habitación.
- Contestar
-
Este proceso implica una dispersión mayor y más uniforme de la materia ya que se permite que el aire comprimido en el bote se expanda hacia el aire de menor presión de la habitación. El proceso también requiere una entrada de energía para interrumpir las fuerzas intermoleculares entre las moléculas de gas muy espaciadas que originalmente se comprimen en el contenedor. Si tocaras la boquilla del bote, notarías que hace frío porque las moléculas que salen están quitando energía de sus alrededores, y el bote es parte del entorno.
Resumen
Los procesos químicos y físicos tienen una tendencia natural a ocurrir en una dirección bajo ciertas condiciones. Un proceso espontáneo ocurre sin la necesidad de un aporte continuo de energía de alguna fuente externa, mientras que un proceso no espontáneo lo requiere. Los sistemas sometidos a un proceso espontáneo pueden experimentar o no una ganancia o pérdida de energía, pero experimentarán un cambio en la forma en que la materia y/o la energía se distribuyen dentro del sistema. En esta sección solo hemos discutido la desintegración nuclear, cambios físicos de sustancias puras y eventos macroscópicos como el agua que fluye cuesta abajo. En las siguientes secciones discutiremos mezclas y reacciones químicas, situaciones en las que la descripción de la esponteneidad se vuelve más desafiante.
Glosario
- proceso no espontáneo
- proceso que requiere entrada continua de energía de una fuente externa
- cambio espontáneo
- proceso que se lleva a cabo sin una entrada continua de energía de una fuente externa