16.E: Termodinámica (Ejercicios)

16.1: Ejercicios de Espontaneidad

Q16.1.1

¿Qué es una reacción espontánea?

S16.1.1

Una reacción tiene una tendencia natural a ocurrir y tiene lugar sin el aporte continuo de energía de una fuente externa.

Q16.1.2

¿Qué es una reacción no espontánea?

Q16.1.3

Indicar si los siguientes procesos son espontáneos o no espontáneos.

1. Congelación de agua líquida a una temperatura por debajo de su punto de congelación
2. Congelación de agua líquida a una temperatura superior a su punto de congelación
3. La combustión de la gasolina
4. Una pelota lanzada al aire
5. Una gota de lluvia cayendo al suelo
6. Oxidado de hierro en un ambiente húmedo

S16.1.2

espontáneo; no espontáneo; espontáneo; no espontáneo; espontáneo; espontáneo

Q16.1.4

Un globo lleno de helio se desinfla espontáneamente durante la noche mientras los átomos de He se difunden a través de la pared del globo Describir la redistribución de la materia y/o energía que acompaña a este proceso.

Q16.1.5

Muchos materiales plásticos son polímeros orgánicos que contienen carbono e hidrógeno. La oxidación de estos plásticos en el aire para formar dióxido de carbono y agua es un proceso espontáneo; sin embargo, los materiales plásticos tienden a persistir en el ambiente. Explique.

S16.1.5

Aunque la oxidación de los plásticos es espontánea, la tasa de oxidación es muy lenta. Por lo tanto, los plásticos son cinéticamente estables y no se descomponen apreciablemente incluso durante períodos de tiempo relativamente largos.

16.2: Ejercicios de entropía

Q16.2.1

En la siguiente Figura se muestran todas las distribuciones y microestados posibles para cuatro partículas diferentes compartidas entre dos cajas. Determinar el cambio de entropía, Δ S, si las partículas se distribuyen inicialmente de manera uniforme entre las dos cajas, pero al redistribuir todas terminan en la Caja (b).

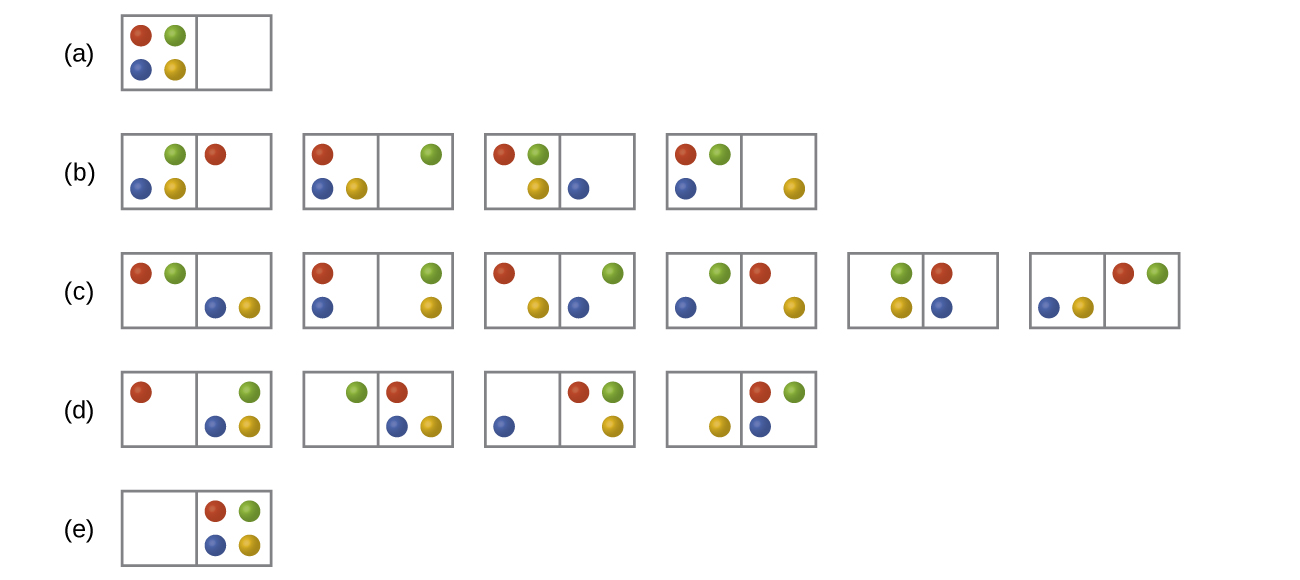
Q16.2.2

En la Figura se muestran todas las distribuciones y microestados posibles para cuatro partículas diferentes compartidas entre dos cajas. Determinar el cambio de entropía, Δ S, para el sistema cuando se convierte de distribución a distribución (d).

S16.2.2

Hay cuatro microestados iniciales y cuatro microestados finales.

\[ΔS=k\ln\dfrac{W_\ce{f}}{W_\ce{i}}=\mathrm{1.38×10^{−23}\:J/K×\ln\dfrac{4}{4}=0}\]

Q16.2.3

¿Cómo se relaciona el proceso descrito en el ítem anterior con el sistema mostrado en [link]?

Q16.2.4

Considera un sistema similar al de abajo, excepto que contiene seis partículas en lugar de cuatro. ¿Cuál es la probabilidad de tener todas las partículas en solo una de las dos cajas del estuche? Compárelo con la probabilidad similar de que el sistema de cuatro partículas que hemos derivado sea igual a\(\dfrac{1}{8}\). ¿Qué nos dice esta comparación sobre sistemas aún más grandes?

S16.2.4

La probabilidad de que todas las partículas estén en un lado es\(\dfrac{1}{32}\). Esta probabilidad es notablemente menor que el\(\dfrac{1}{8}\) resultado para el sistema de cuatro partículas. La conclusión que podemos llegar es que la probabilidad de que todas las partículas permanezcan en una sola parte del sistema disminuirá rápidamente a medida que aumenta el número de partículas y, por ejemplo, la probabilidad de que todas las moléculas de gas se reúnan en un solo lado de una habitación a temperatura y presión ambiente es insignificante ya que el número de moléculas de gas en la habitación es muy grande.

Q16.2.5

Considera el sistema que se muestra en la Figura. ¿Cuál es el cambio en la entropía para el proceso donde la energía se asocia inicialmente solo con la partícula A, pero en el estado final la energía se distribuye entre dos partículas diferentes?

Q16.2.6

Considera el sistema que se muestra en la Figura. ¿Cuál es el cambio en la entropía para el proceso donde la energía se asocia inicialmente con las partículas A y B, y la energía se distribuye entre dos partículas en diferentes cajas (una en A-B y la otra en C-D)?

S16.2.6

Sólo hay un estado inicial. Para el estado final, la energía puede estar contenida en pares A-C, A-D, B-C o B-D. De esta manera, hay cuatro estados finales posibles.

\[ΔS=k\ln\left(\dfrac{W_\ce{f}}{W_\ce{i}}\right)=\mathrm{1.38×10^{−23}\:J/K×\ln\left(\dfrac{4}{1}\right)=1.91×10^{−23}\:J/K}\]

Q16.2.7

Organizar los siguientes conjuntos de sistemas en orden de entropía creciente. Asumir un mol de cada sustancia y la misma temperatura para cada miembro de un conjunto.

1. H ₂ (g), HBro ₄ (g), HBr (g)
2. H ₂ O (l), H ₂ O (g), H ₂ O (s)
3. Él (g), Cl ₂ (g), P ₄ (g)

Q16.2.8

A temperatura ambiente, la entropía de los halógenos aumenta de I ₂ a Br ₂ a Cl ₂. Explique.

S16.2.8

Las masas de estas moléculas sugerirían la tendencia opuesta en sus entropías. La tendencia observada es el resultado de la variación más significativa de la entropía con un estado físico. A temperatura ambiente, I ₂ es un sólido, Br ₂ es un líquido y Cl ₂ es un gas.

Q16.2.9

Considera dos procesos: sublimación de I ₂ (s) y fusión de I ₂ (s) (Nota: este último proceso puede ocurrir a la misma temperatura pero presión algo mayor).

\[\ce{I2}(s)⟶\ce{I2}(g)\]

\[\ce{I2}(s)⟶\ce{I2}(l)\]

¿El Δ S es positivo o negativo en estos procesos? ¿En cuál de los procesos será mayor la magnitud del cambio de entropía?

Q16.2.11

Indicar qué sustancia en los pares dados tiene el mayor valor de entropía. Explique sus elecciones.

1. C ₂ H ₅ OH (l) o C ₃ H ₇ OH (l)
2. C ₂ H ₅ OH (l) o C ₂ H ₅ OH (g)
3. 2Hor H (g)

S16.2.11

C ₃ H ₇ OH (l) ya que es una molécula más grande (más compleja y más masiva), por lo que más microestados que describen sus movimientos están disponibles a cualquier temperatura dada. C ₂ H ₅ OH (g) como está en estado gaseoso. 2H (g), ya que la entropía es una propiedad extensa, y así dos átomos de H (o dos moles de átomos de H) poseen el doble de entropía que un átomo (o un mol de átomos).

Q16.2.11

Predecir el signo del cambio de entropía para los siguientes procesos:

1. Un cubito de hielo se calienta cerca de su punto de fusión.
2. El aliento exhalado forma niebla en una mañana fría.
3. La nieve se derrite.

Q16.2.12

Predecir el signo del cambio de entalpía para los siguientes procesos. Da una razón para tu predicción.

1. \(\ce{Pb^2+}(aq)+\ce{S^2-}(aq)⟶\ce{PbS}(s)\)
2. \(\ce{2Fe}(s)+\ce{3O2}(g)⟶\ce{Fe2O3}(s)\)
3. \(\ce{2C6H14}(l)+\ce{19O2}(g)⟶\ce{14H2O}(g)+\ce{12CO2}(g)\)

S16.2.12

Negativo. La precipitación sólida relativamente ordenada disminuye el número de iones móviles en solución. Negativo. Hay una pérdida neta de tres moles de gas desde los reactivos hasta los productos. Positivo. Hay un incremento neto de siete moles de gas de los reactivos a los productos.

Q16.2.13

Escribir la ecuación química balanceada para la combustión de metano, CH ₄ (g), para dar dióxido de carbono y vapor de agua. Explique por qué es difícil predecir si Δ S es positivo o negativo para esta reacción química.

Q16.2.14

Escribir la ecuación química balanceada para la combustión del benceno, C ₆ H ₆ (l), para dar dióxido de carbono y vapor de agua. ¿Esperaría que Δ S fuera positivo o negativo en este proceso?

S16.2.14

\[\ce{C6H6}(l)+7.5\ce{O2}(g)⟶\ce{3H2O}(g)+\ce{6CO2}(g)\]

Hay 7.5 moles de gas inicialmente, y 3 + 6 = 9 moles de gas al final. Por lo tanto, es probable que la entropía aumente como resultado de esta reacción, y Δ S sea positiva.

16.3: La Segunda y Tercera Ley

Q16.3.0

¿Cuál es la diferencia entre Δ S, Δ S°, y\(ΔS^\circ_{298}\) para un cambio químico?

Q16.3.1

Calcular\(ΔS^\circ_{298}\) para los siguientes cambios.

1. \(\ce{SnCl4}(l)⟶\ce{SnCl4}(g)\)
2. \(\ce{CS2}(g)⟶\ce{CS2}(l)\)
3. \(\ce{Cu}(s)⟶\ce{Cu}(g)\)
4. \(\ce{H2O}(l)⟶\ce{H2O}(g)\)
5. \(\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(l)\)
6. \(\ce{2HCl}(g)+\ce{Pb}(s)⟶\ce{PbCl2}(s)+\ce{H2}(g)\)
7. \(\ce{Zn}(s)+\ce{CuSO4}(s)⟶\ce{Cu}(s)+\ce{ZnSO4}(s)\)

S16.3.1

107 J/K; −86,4 J/K; 133,2 J/K; 118,8 J/K; −326,6 J/K; −171,9 J/K; (g) −7.2 J/K

Q16.3.2

Determinar el cambio de entropía para la combustión de etanol líquido, C ₂ H ₅ OH, bajo condiciones de estado estándar para dar dióxido de carbono gaseoso y agua líquida.

Q16.3.3

Determinar el cambio de entropía para la combustión de propano gaseoso, C ₃ H ₈, bajo condiciones de estado estándar para dar dióxido de carbono gaseoso y agua.

S16.3.3

100.6 J/K

Q16.3.4

Las reacciones de “termita” se han utilizado para soldar piezas metálicas como rieles ferroviarios y en refinación de metales. Una de tales reacciones de termita es:

\[\ce{Fe2O3}(s)+\ce{2Al}(s)⟶\ce{Al2O3}(s)+\ce{2Fe}(s)\]

¿La reacción es espontánea a temperatura ambiente bajo condiciones estándar? Durante la reacción, los alrededores absorben 851.8 kJ/mol de calor.

Q16.3.5

Utilizando los\(S^\circ_{298}\) valores relevantes enumerados en el Apéndice G, calcule\(S^\circ_{298}\) para los siguientes cambios:

1. \(\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g)\)
2. \(\ce{N2}(g)+\dfrac{5}{2}\ce{O2}(g)⟶\ce{N2O5}(g)\)

S16.3.5

−198,1 J/K; −348,9 J/K

Q16.3.6

A partir de la siguiente información, determine\(ΔS^\circ_{298}\) para lo siguiente:

1. \(\ce{N}(g)+\ce{O}(g)⟶\ce{NO}(g) \hspace{20px} ΔS^\circ_{298}=\,?\)
2. \(\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g) \hspace{20px} ΔS^\circ_{298}=\mathrm{24.8\: J/K}\)
3. \(\ce{N2}(g)⟶\ce{2N}(g) \hspace{20px} ΔS^\circ_{298}=\mathrm{115.0\: J/K}\)
4. \(\ce{O2}(g)⟶\ce{2O}(g) \hspace{20px} ΔS^\circ_{298}=\mathrm{117.0\: J/K}\)

Q16.3.7

Al calcular Δ S _univ a cada temperatura, determinar si la fusión de 1 mol de NaCl (s) es espontánea a 500 °C y a 700 °C.

\[S^\circ_{\ce{NaCl}(s)}=\mathrm{72.11\:\dfrac{J}{mol⋅K}}\hspace{40px} S^\circ_{\ce{NaCl}(l)}=\mathrm{95.06\:\dfrac{J}{mol⋅K}}\hspace{40px ΔH^\circ_\ce{fusion}=\mathrm{27.95\: kJ/mol}\]

¿Qué suposiciones se hacen sobre la información termodinámica (valores de entropía y entalpía) utilizada para resolver este problema?

S16.3.7

Como Δ S _univ < 0 a cada una de estas temperaturas, la fusión no es espontánea en ninguna de ellas. Los valores dados para entropía y entalpía son para NaCl a 298 K. Se supone que estos no cambian significativamente a las temperaturas más altas utilizadas en el problema.

Q16.3.8

Utilice los datos estándar de entropía del Apéndice G para determinar el cambio en la entropía para cada una de las reacciones enumeradas en [link]. Todos se ejecutan en condiciones estatales estándar y 25 °C.

Q16.3.8

2.86 J/K; 24.8 J/K; −113.2 J/K; −24.7 J/K; 15.5 J/K; 290.0 J/K

16.4: Energía Libre

Q16.4.1

¿Cuál es la diferencia entre Δ G, Δ G°, y\(ΔG^\circ_{298}\) para un cambio químico?

Q16.4.2

A reacciones tiene\(ΔH^\circ_{298}\) = 100 kJ/mol y\(ΔS^\circ_{298}=\textrm{250 J/mol⋅K}\). ¿La reacción es espontánea a temperatura ambiente? De no ser así, ¿bajo qué condiciones de temperatura se volverá espontáneo?

S16.4.2

La reacción es no espontánea a temperatura ambiente. Por encima de 400 K, Δ G se volverá negativo, y la reacción se volverá espontánea.

Q16.4.3

Explica lo que sucede cuando una reacción comienza con Δ G < 0 (negativo) y alcanza el punto donde Δ G = 0.

Utilice los datos estándar de energía libre de formación en el Apéndice G para determinar el cambio de energía libre para cada una de las siguientes reacciones, las cuales se ejecutan en condiciones de estado estándar y 25 °C. Identifique cada una como espontánea o no espontánea en estas condiciones.

1. \(\ce{MnO2}(s)⟶\ce{Mn}(s)+\ce{O2}(g)\)
2. \(\ce{H2}(g)+\ce{Br2}(l)⟶\ce{2HBr}(g)\)
3. \(\ce{Cu}(s)+\ce{S}(g)⟶\ce{CuS}(s)\)
4. \(\ce{2LiOH}(s)+\ce{CO2}(g)⟶\ce{Li2CO3}(s)+\ce{H2O}(g)\)
5. \(\ce{CH4}(g)+\ce{O2}(g)⟶\ce{C}(s,\,\ce{graphite})+\ce{2H2O}(g)\)
6. \(\ce{CS2}(g)+\ce{3Cl2}(g)⟶\ce{CCl4}(g)+\ce{S2Cl2}(g)\)

S16.4.3

465.1 kJ no espontáneo; −106.86 kJ espontáneo; −53.6 kJ espontáneo; −83.4 kJ espontáneo; −406.7 kJ espontáneo; −30.0 kJ espontáneo

Q16.4.4

Utilice los datos estándar de energía libre en el Apéndice G para determinar el cambio de energía libre para cada una de las siguientes reacciones, las cuales se ejecutan en condiciones de estado estándar y 25 °C. Identifique cada una como espontánea o no espontánea en estas condiciones.

1. \(\ce{C}(s,\, \ce{graphite})+\ce{O2}(g)⟶\ce{CO2}(g)\)
2. \(\ce{O2}(g)+\ce{N2}(g)⟶\ce{2NO}(g)\)
3. \(\ce{2Cu}(s)+\ce{S}(g)⟶\ce{Cu2S}(s)\)
4. \(\ce{CaO}(s)+\ce{H2O}(l)⟶\ce{Ca(OH)2}(s)\)
5. \(\ce{Fe2O3}(s)+\ce{3CO}(g)⟶\ce{2Fe}(s)+\ce{3CO2}(g)\)
6. \(\ce{CaSO4⋅2H2O}(s)⟶\ce{CaSO4}(s)+\ce{2H2O}(g)\)

Dado:

\[\ce{P4}(s)+\ce{5O2}(g)⟶\ce{P4O10}(s) \hspace{20px} ΔG^\circ_{298}=\mathrm{−2697.0\: kJ/mol}\]

\[\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(g) \hspace{20px} ΔG^\circ_{298}=\mathrm{−457.18\: kJ/mol}\]

\[\ce{6H2O}(g)+\ce{P4O10}(g)⟶\ce{4H3PO4}(l) \hspace{20px} ΔG^\circ_{298}=\mathrm{−428.66\: kJ/mol}\]

Q16.4.5

1. Determinar la energía libre estándar de formación,\(ΔG^\circ_\ce{f}\), para el ácido fosfórico.
2. ¿Cómo se compara su resultado calculado con el valor del Apéndice G? Explique.

S16.4.5

−1124.3 kJ/mol para el cambio de energía libre estándar. El cálculo concuerda con el valor en el Apéndice G porque la energía libre es una función de estado (al igual que la entalpía y entropía), por lo que su cambio depende únicamente de los estados inicial y final, no del camino entre ellos.

Q16.4.6

¿La formación de ozono (O ₃ (g)) a partir del oxígeno (O ₂ (g)) es espontánea a temperatura ambiente bajo condiciones de estado estándar?

Q16.4.7

Considerar la descomposición del óxido rojo de mercurio (II) bajo condiciones de estado estándar.

\[\ce{2HgO}(s,\,\ce{red})⟶\ce{2Hg}(l)+\ce{O2}(g)\]

1. ¿La descomposición es espontánea bajo condiciones estándar del estado?
2. ¿Por encima de qué temperatura se vuelve espontánea la reacción?

S16.4.7

La reacción es no espontánea; Por encima de 566 °C el proceso es espontáneo.

Q16.4.8

Entre otras cosas, un combustible ideal para los propulsores de control de un vehículo espacial debe descomponerse en una reacción exotérmica espontánea cuando se expone al catalizador apropiado. Evaluar las siguientes sustancias bajo condiciones estatales estándar como candidatos adecuados para combustibles.

1. Amoníaco:\(\ce{2NH3}(g)⟶\ce{N2}(g)+\ce{3H2}(g)\)
2. Diborano:\(\ce{B2H6}(g)⟶\ce{2B}(g)+\ce{3H2}(g)\)
3. Hidrazina:\(\ce{N2H4}(g)⟶\ce{N2}(g)+\ce{2H2}(g)\)
4. Peróxido de hidrógeno:\(\ce{H2O2}(l)⟶\ce{H2O}(g)+\dfrac{1}{2}\ce{O2}(g)\)

Q16.4.9

Calcular Δ G° para cada una de las siguientes reacciones a partir de la constante de equilibrio a la temperatura dada.

1. \(\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g) \hspace{20px} \mathrm{T=2000\:°C} \hspace{20px} K_p=4.1×10^{−4}\)
2. \(\ce{H2}(g)+\ce{I2}(g)⟶\ce{2HI}(g) \hspace{20px} \mathrm{T=400\:°C} \hspace{20px} K_p=50.0\)
3. \(\ce{CO2}(g)+\ce{H2}(g)⟶\ce{CO}(g)+\ce{H2O}(g) \hspace{20px} \mathrm{T=980\:°C} \hspace{20px} K_p=1.67\)
4. \(\ce{CaCO3}(s)⟶\ce{CaO}(s)+\ce{CO2}(g) \hspace{20px} \mathrm{T=900\:°C} \hspace{20px} K_p=1.04\)
5. \(\ce{HF}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{F-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=7.2×10^{−4}\)
6. \(\ce{AgBr}(s)⟶\ce{Ag+}(aq)+\ce{Br-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=3.3×10^{−13}\)

S16.4.9

1.5 × 10 ² kJ; −21.9 kJ; −5.34 kJ; −0.383 kJ; 18 kJ; 71 kJ

Q16.4.10

Calcular Δ G° para cada una de las siguientes reacciones a partir de la constante de equilibrio a la temperatura dada.

1. \(\ce{Cl2}(g)+\ce{Br2}(g)⟶\ce{2BrCl}(g) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=4.7×10^{−2}\)
2. \(\ce{2SO2}(g)+\ce{O2}(g)⇌\ce{2SO3}(g) \hspace{20px} \mathrm{T=500\:°C} \hspace{20px} K_p=48.2\)
3. \(\ce{H2O}(l)⇌\ce{H2O}(g) \hspace{20px} \mathrm{T=60\:°C} \hspace{20px} K_p=\mathrm{0.196\: atm}\)
4. \(\ce{CoO}(s)+\ce{CO}(g)⇌\ce{Co}(s)+\ce{CO2}(g) \hspace{20px} \mathrm{T=550\:°C} \hspace{20px} K_p=4.90×10^2\)
5. \(\ce{CH3NH2}(aq)+\ce{H2O}(l)⟶\ce{CH3NH3+}(aq)+\ce{OH-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=4.4×10^{−4}\)
6. \(\ce{PbI2}(s)⟶\ce{Pb^2+}(aq)+\ce{2I-}(aq) \hspace{20px} \mathrm{T=25\:°C} \hspace{20px} K_p=8.7×10^{−9}\)

Q16.4.11

Calcular la constante de equilibrio a 25 °C para cada una de las siguientes reacciones a partir del valor de Δ G° dado.

1. \(\ce{O2}(g)+\ce{2F2}(g)⟶\ce{2OF2}(g) \hspace{20px} ΔG°=\mathrm{−9.2\: kJ}\)
2. \(\ce{I2}(s)+\ce{Br2}(l)⟶\ce{2IBr}(g) \hspace{20px} ΔG°=\mathrm{7.3\: kJ}\)
3. \(\ce{2LiOH}(s)+\ce{CO2}(g)⟶\ce{Li2CO3}(s)+\ce{H2O}(g) \hspace{20px} ΔG°=\mathrm{−79\: kJ}\)
4. \(\ce{N2O3}(g)⟶\ce{NO}(g)+\ce{NO2}(g) \hspace{20px} ΔG°=\mathrm{−1.6\: kJ}\)
5. \(\ce{SnCl4}(l)⟶\ce{SnCl4}(l) \hspace{20px} ΔG°=\mathrm{8.0\: kJ}\)

S16.4.11

K = 41; K = 0.053; K = 6.9 × 10 ¹³; K = 1.9; K = 0.04

Q16.4.2

Calcular la constante de equilibrio a 25 °C para cada una de las siguientes reacciones a partir del valor de Δ G° dado.

1. \(\ce{I2}(s)+\ce{Cl2}(g)⟶\ce{2ICl}(g) \hspace{20px} ΔG°=\mathrm{−10.88\: kJ}\)
2. \(\ce{H2}(g)+\ce{I2}(s)⟶\ce{2HI}(g) \hspace{20px} ΔG°=\mathrm{3.4\: kJ}\)
3. \(\ce{CS2}(g)+\ce{3Cl2}(g)⟶\ce{CCl4}(g)+\ce{S2Cl2}(g) \hspace{20px} ΔG°=\mathrm{−39\: kJ}\)
4. \(\ce{2SO2}(g)+\ce{O2}(g)⟶\ce{2SO3}(g) \hspace{20px} ΔG°=\mathrm{−141.82\: kJ}\)
5. \(\ce{CS2}(g)⟶\ce{CS2}(l) \hspace{20px} ΔG°=\mathrm{−1.88\: kJ}\)

Q16.4.13

Calcular la constante de equilibrio a la temperatura dada.

1. (a)\(\ce{O2}(g)+\ce{2F2}(g)⟶\ce{2F2O}(g) \hspace{20px} \mathrm{(T=100\:°C)}\)
2. \(\ce{I2}(s)+\ce{Br2}(l)⟶\ce{2IBr}(g) \hspace{20px} \mathrm{(T=0.0\:°C)}\)
3. \(\ce{2LiOH}(s)+\ce{CO2}(g)⟶\ce{Li2CO3}(s)+\ce{H2O}(g) \hspace{20px} \mathrm{(T=575\:°C)}\)
4. \(\ce{N2O3}(g)⟶\ce{NO}(g)+\ce{NO2}(g) \hspace{20px} \mathrm{(T=−10.0\:°C)}\)
5. \(\ce{SnCl4}(l)⟶\ce{SnCl4}(g) \hspace{20px} \mathrm{(T=200\:°C)}\)

S16.4.13

En cada una de las siguientes, el valor de Δ G no se da a la temperatura de la reacción. Por lo tanto, debemos calcular Δ G° a partir de los valores Δ H° y Δ S° y luego calcular Δ G a partir de la relación ΔG° = ΔH° − TΔS°.

1. K = 1.29
2. K = 2.51 × 10 ⁻³
3. K = 4.83 × 10 ³
4. K = 0.219
5. K = 16.1

Q16.4.14

Calcular la constante de equilibrio a la temperatura dada.

1. (a)\(\ce{I2}(s)+\ce{Cl2}(g)⟶\ce{2ICl}(g) \hspace{20px} \mathrm{(T=100\:°C)}\)
2. \(\ce{H2}(g)+\ce{I2}(s)⟶\ce{2HI}(g) \hspace{20px} \mathrm{(T=0.0\:°C)}\)
3. \(\ce{CS2}(g)+\ce{3Cl2}(g)⟶\ce{CCl4}(g)+\ce{S2Cl2}(g) \hspace{20px} \mathrm{(T=125\:°C)}\)
4. \(\ce{2SO2}(g)+\ce{O2}(g)⟶\ce{2SO3}(g) \hspace{20px} \mathrm{(T=675\:°C)}\)
5. \(\ce{CS2}(g)⟶\ce{CS2}(l) \hspace{20px} \mathrm{(T=90\:°C)}\)

Q16.4.15

Considere la siguiente reacción a 298 K:

\[\ce{N2O4}(g)⇌\ce{2NO2}(g) \hspace{20px} K_P=0.142\]

¿Cuál es el cambio estándar de energía libre a esta temperatura? Describir lo que sucede con el sistema inicial, donde los reactivos y productos se encuentran en estados estándar, a medida que se acerca al equilibrio.

S16.4.16

El cambio de energía libre estándar es\(ΔG^\circ_{298}=−RT\ln K=\mathrm{4.84\: kJ/mol}\). Cuando los reactivos y productos están en sus estados estándar (1 bar o 1 atm), Q = 1. A medida que la reacción avanza hacia el equilibrio, la reacción se desplaza a la izquierda (la cantidad de productos disminuye mientras la cantidad de reactivos aumenta): Q < 1, y\(ΔG_{298}\) se vuelve menos positiva a medida que se acerca a cero. En equilibrio, Q = K y Δ G = 0.

Q16.4.17

Determinar el punto de ebullición normal (en kelvin) del dicloroetano, CH ₂ Cl ₂. Encuentre el punto de ebullición real usando Internet o alguna otra fuente, y calcule el porcentaje de error en la temperatura. Explique las diferencias, en su caso, entre los dos valores.

Q16.4.18

¿Bajo qué condiciones es\(\ce{N2O3}(g)⟶\ce{NO}(g)+\ce{NO2}(g)\) espontáneo?

S16.4.18

La reacción será espontánea a temperaturas superiores a 287 K.

Q16.4.19

A temperatura ambiente, la constante de equilibrio (K _w) para la autoionización del agua es 1.00 × 10 ⁻¹⁴. Con esta información, se calcula el cambio estándar de energía libre para la reacción acuosa del ion hidrógeno con el ion hidróxido para producir agua. (Pista: La reacción es la inversa de la reacción de autoionización.)

Q16.4.20

El sulfuro de hidrógeno es un contaminante que se encuentra en el gas natural. Después de su eliminación, se convierte en azufre por la reacción\(\ce{2H2S}(g)+\ce{SO2}(g)⇌\dfrac{3}{8}\ce{S8}(s,\,\ce{rhombic})+\ce{2H2O}(l)\). ¿Cuál es la constante de equilibrio para esta reacción? ¿La reacción es endotérmica o exotérmica?

S16.4.20

K = 5.35 × 10 ¹⁵

El proceso es exotérmico.

Q16.4.21

Considere la descomposición de CaCo ₃ (s) en CaO (s) y CO ₂ (g). ¿Cuál es la presión parcial de equilibrio del CO ₂ a temperatura ambiente?

Q16.4.22

En el laboratorio, el cloruro de hidrógeno (HCl (g)) y el amoníaco (NH ₃ (g)) a menudo escapan de las botellas de sus soluciones y reaccionan para formar el cloruro de amonio (NH ₄ Cl (s)), el esmalte blanco que a menudo se ve en la cristalería. Suponiendo que el número de moles de cada gas que escapa a la habitación es el mismo, ¿cuál es la presión parcial máxima de HCl y NH ₃ en el laboratorio a temperatura ambiente? (Sugerencia: Las presiones parciales serán iguales y están en su valor máximo cuando están en equilibrio.)

S16.4.22

1.0 × 10 ⁻⁸ atm. Esta es la presión máxima de los gases bajo las condiciones señaladas.

Q16.4.23

El benceno se puede preparar a partir de acetileno. \(\ce{3C2H2}(g)⇌\ce{C6H6}(g)\). Determinar la constante de equilibrio a 25 °C y 850 °C. ¿La reacción es espontánea a alguna de estas temperaturas? ¿Por qué no se encuentra todo el acetileno como benceno?

Q16.4.24

El dióxido de carbono se descompone en CO y O ₂ a temperaturas elevadas. ¿Cuál es la presión parcial de equilibrio del oxígeno en una muestra a 1000 °C para la cual la presión inicial de CO ₂ fue de 1.15 atm?

\[x=\mathrm{1.29×10^{−5}\:atm}=P_{\ce{O2}}\]

Q16.4.25

El tetracloruro de carbono, un importante disolvente industrial, se prepara mediante la cloración de metano a 850 K.

\[\ce{CH4}(g)+\ce{4Cl2}(g)⟶\ce{CCl4}(g)+\ce{4HCl}(g)\]

¿Cuál es la constante de equilibrio para la reacción a 850 K? ¿Necesitaría calentarse o enfriarse el recipiente de reacción para mantener constante la temperatura de la reacción?

Q16.4.25B

El ácido acético, CH ₃ CO ₂ H, puede formar un dímero, (CH ₃ CO ₂ H) ₂, en fase gaseosa.

\[\ce{2CH3CO2H}(g)⟶\ce{(CH3CO2H)2}(g)\]

El dímero se mantiene unido por dos enlaces de hidrógeno con una fuerza total de 66.5 kJ por mol de dímero.

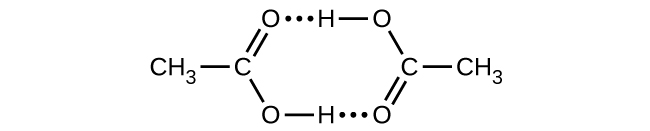
A 25 °C, la constante de equilibrio para la dimerización es de 1.3 × 10 ³ (presión en atm). ¿Qué es Δ S° para la reacción?

S16.4.25B

−0.16 kJ

Q16.4.26

El ácido nítrico, HNO ₃, se puede preparar mediante la siguiente secuencia de reacciones:

\[\ce{4NH3}(g)+\ce{5O2}(g)⟶\ce{4NO}(g)+\ce{6H2O}(g)\]

\[\ce{2NO}(g)+\ce{O2}(g)⟶\ce{2NO2}(g)\]

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(l)+\ce{NO}(g)\]

How much heat is evolved when 1 mol of NH₃(g) is converted to HNO₃(l)? Assume standard states at 25 °C.

Q16.4.27A

Determine ΔG for the following reactions.

(a) Antimony pentachloride decomposes at 448 °C. The reaction is:

\[\ce{SbCl5}(g)⟶\ce{SbCl3}(g)+\ce{Cl2}(g)\]

An equilibrium mixture in a 5.00 L flask at 448 °C contains 3.85 g of SbCl₅, 9.14 g of SbCl₃, and 2.84 g of Cl₂.

Chlorine molecules dissociate according to this reaction:

\[\ce{Cl2}(g)⟶\ce{2Cl}(g)\]

1.00% of Cl₂ molecules dissociate at 975 K and a pressure of 1.00 atm.

S16.4.27A

1. (a) −22.1 kJ;
2. 61.6 kJ/mol

Q16.4.27

Given that the \(ΔG^\circ_\ce{f}\) for Pb²⁺(aq) and Cl⁻(aq) is −24.3 kJ/mole and −131.2 kJ/mole respectively, determine the solubility product, K_sp, for PbCl₂(s).

Q16.4.28

Determine the standard free energy change, \(ΔG^\circ_\ce{f}\), for the formation of S²⁻(aq) given that the \(ΔG^\circ_\ce{f}\) for Ag⁺(aq) and Ag₂S(s) are 77.1 k/mole and −39.5 kJ/mole respectively, and the solubility product for Ag₂S(s) is 8 × 10⁻⁵¹.

S16.4.28

90 kJ/mol

Q16.4.29

Determine the standard enthalpy change, entropy change, and free energy change for the conversion of diamond to graphite. Discuss the spontaneity of the conversion with respect to the enthalpy and entropy changes. Explain why diamond spontaneously changing into graphite is not observed.

Q16.4.30

The evaporation of one mole of water at 298 K has a standard free energy change of 8.58 kJ.

\[\ce{H2O}(l)⇌\ce{H2O}(g) \hspace{20px} ΔG^\circ_{298}=\mathrm{8.58\: kJ}\]

1. (a) Is the evaporation of water under standard thermodynamic conditions spontaneous?
2. Determine the equilibrium constant, K_P, for this physical process.
3. By calculating ∆G, determine if the evaporation of water at 298 K is spontaneous when the partial pressure of water, \(P_{\ce{H2O}}\), is 0.011 atm.
4. If the evaporation of water were always nonspontaneous at room temperature, wet laundry would never dry when placed outside. In order for laundry to dry, what must be the value of \(P_{\ce{H2O}}\) in the air?

S16.4.30

(a) Under standard thermodynamic conditions, the evaporation is nonspontaneous; K_p = 0.031; The evaporation of water is spontaneous; \(P_{\ce{H2O}}\) must always be less than K_p or less than 0.031 atm. 0.031 atm represents air saturated with water vapor at 25 °C, or 100% humidity.

Q16.4.31

In glycolysis, the reaction of glucose (Glu) to form glucose-6-phosphate (G6P) requires ATP to be present as described by the following equation:

\[\mathrm{Glu + ATP ⟶ G6P + ADP} \hspace{20px} ΔG^\circ_{298}=\mathrm{−17\: kJ}\]

In this process, ATP becomes ADP summarized by the following equation:

\[\mathrm{ATP⟶ADP} \hspace{20px} ΔG^\circ_{298}=\mathrm{−30\: kJ}\]

Determine the standard free energy change for the following reaction, and explain why ATP is necessary to drive this process:

\[\mathrm{Glu⟶G6P} \hspace{20px} ΔG^\circ_{298}=\:?\]

Q16.4.32

One of the important reactions in the biochemical pathway glycolysis is the reaction of glucose-6-phosphate (G6P) to form fructose-6-phosphate (F6P):

\[\mathrm{G6P⇌F6P} \hspace{20px} ΔG^\circ_{298}=\mathrm{1.7\: kJ}\]

1. (a) Is the reaction spontaneous or nonspontaneous under standard thermodynamic conditions?
2. Standard thermodynamic conditions imply the concentrations of G6P and F6P to be 1 M, however, in a typical cell, they are not even close to these values. Calculate ΔG when the concentrations of G6P and F6P are 120 μM and 28 μM respectively, and discuss the spontaneity of the forward reaction under these conditions. Assume the temperature is 37 °C.

S16.4.32

(a) Nonspontaneous as \(ΔG^\circ_{298}>0\); \(ΔG^\circ_{298}=−RT\ln K,\) \(ΔG = 1.7×10^3 + \left(8.314 × 335 × \ln\dfrac{28}{128}\right) = \mathrm{−2.5\: kJ}\). The forward reaction to produce F6P is spontaneous under these conditions.

Q16.4.33

Without doing a numerical calculation, determine which of the following will reduce the free energy change for the reaction, that is, make it less positive or more negative, when the temperature is increased. Explain.

1. (a) \(\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g)\)
2. \(\ce{HCl}(g)+\ce{NH3}(g)⟶\ce{NH4Cl}(s)\)
3. \(\ce{(NH4)2Cr2O7}(s)⟶\ce{Cr2O3}(s)+\ce{4H2O}(g)+\ce{N2}(g)\)
4. \(\ce{2Fe}(s)+\ce{3O2}(g)⟶\ce{Fe2O3}(s)\)

When ammonium chloride is added to water and stirred, it dissolves spontaneously and the resulting solution feels cold. Without doing any calculations, deduce the signs of ΔG, ΔH, and ΔS for this process, and justify your choices.

S16.4.33

ΔG is negative as the process is spontaneous. ΔH is positive as with the solution becoming cold, the dissolving must be endothermic. ΔS must be positive as this drives the process, and it is expected for the dissolution of any soluble ionic compound.

Q16.4.34

An important source of copper is from the copper ore, chalcocite, a form of copper(I) sulfide. When heated, the Cu₂S decomposes to form copper and sulfur described by the following equation:

\[\ce{Cu2S}(s)⟶\ce{Cu}(s)+\ce{S}(s)\]

1. (a) Determine \(ΔG^\circ_{298}\) for the decomposition of Cu₂S(s).
2. The reaction of sulfur with oxygen yields sulfur dioxide as the only product. Write an equation that describes this reaction, and determine \(ΔG^\circ_{298}\) for the process.
3. The production of copper from chalcocite is performed by roasting the Cu₂S in air to produce the Cu. By combining the equations from Parts (a) and (b), write the equation that describes the roasting of the chalcocite, and explain why coupling these reactions together makes for a more efficient process for the production of the copper.

Q16.4.35

What happens to \(ΔG^\circ_{298}\) (becomes more negative or more positive) for the following chemical reactions when the partial pressure of oxygen is increased?

1. (a) \(\ce{S}(s)+\ce{O2}(g)⟶\ce{SO2}(g)\)
2. \(\ce{2SO2}(g)+\ce{O2}(g)⟶\ce{SO3}(g)\)
3. \(\ce{HgO}(s)⟶\ce{Hg}(l)+\ce{O2}(g)\)

S16.4.35

1. (a) Increasing \(P_{\ce{O2}}\) will shift the equilibrium toward the products, which increases the value of K. \(ΔG^\circ_{298}\) therefore becomes more negative.
2. Increasing \(P_{\ce{O2}}\) will shift the equilibrium toward the products, which increases the value of K. \(ΔG^\circ_{298}\) therefore becomes more negative.
3. Increasing \(P_{\ce{O2}}\) will shift the equilibrium the reactants, which decreases the value of K. \(ΔG^\circ_{298}\) therefore becomes more positive.