4.9: Integración

Hay información adicional obtenida de la espectroscopía de RMN ^1H que normalmente no está disponible a partir de la espectroscopía de RMN ¹³ C. El desplazamiento químico puede mostrar cuántos tipos diferentes de hidrógenos se encuentran en una molécula; la integración revela el número de hidrógenos de cada tipo.

Al observar el espectro del etanol, se puede ver que hay tres tipos diferentes de hidrógenos en la molécula. También se puede ver por integración que hay tres hidrógenos de un tipo, dos del segundo tipo, y uno del tercer tipo —correspondientes al grupo CH ₃ o metilo, al grupo CH ₂ o metileno y al grupo OH o hidroxilo. Esa información ayuda a reducir el número de posibles estructuras de la muestra, por lo que facilita mucho la elucidación de la estructura de una muestra desconocida.

• la integración revela la relación de un tipo de hidrógeno a otro dentro de una molécula.

Los datos integrales se pueden dar en diferentes formas. Debes estar al tanto de todas ellas. En forma cruda, una integral es una línea horizontal que recorre el espectro de izquierda a derecha. Donde la línea cruza la frecuencia de un pico, se mide el área del pico. Esta medición se muestra como un salto o paso hacia arriba en la línea integral; la distancia vertical que sube la línea es proporcional al área del pico. El área está relacionada con la cantidad de ondas de radio absorbidas a esa frecuencia, y la cantidad de ondas de radio absorbidas es proporcional al número de átomos de hidrógeno que absorben las ondas de radio.

El siguiente espectro se registró con una muestra de etanol en deuterocloroformo (CdCl ₃). El etanol tiene la fórmula condensada CH ₃ CH ₂ OH. Su espectro de RMN ^1H debe reflejar una relación 3:2:1 de hidrógenos.

Esas proporciones se muestran por la altura que la línea integral azul “salta” o “escalona” a medida que pasa por cada pico. Hay tres picos en etanol: un pico agudo cerca de 4 ppm, una pequeña mancha cerca de 1.5 ppm y otro pico agudo cerca de 1 ppm. El primer paso en la línea integral, cerca de 4 ppm, es bastante grande. El segundo escalón, cerca de 1.5 ppm, es solo aproximadamente la mitad de grande que el primero. El tercer paso, cerca de 1 ppm, parece un poco más grande que el primero. Sin sacar un gobernante, es difícil juzgar exactamente qué tan grande, pero tal vez sea 1.5 veces más grande que el primero.

Figura\(\PageIndex{1}\): Espectro de RMN ^1H de etanol con línea integral continua.

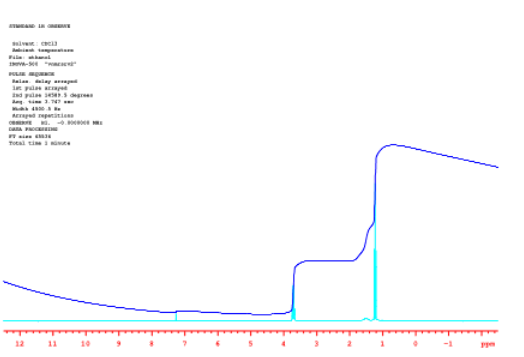
Fuente: Espectro tomado en CdCl ₃ en un Espectrómetro Varian Gemini 2000 con imán Oxford de 300 MHz.

Eso significa que la relación de estos picos es 1:0. 5:1 .5. Eso es lo mismo que una relación 2:1:3. Probablemente estamos viendo, de izquierda a derecha, el CH ₂, el OH y el CH ₃ en el etanol.

Volveremos a mirar esa proporción dentro del etanol en un momento. En tanto, vale la pena señalar que hay un pico adicional, pequeño en el espectro cercano a 7.25 ppm. Eso es un poco de cloroformo regular, CHCl ₃, en el disolvente CDCl ₃ utilizado para el espectro de RMN. Se podría imaginar que es bastante difícil separar dos compuestos que difieren entre sí sólo por la presencia o ausencia de un neutrón. En consecuencia, siempre hay una pequeña cantidad de CHCl ₃ en una botella de CdCl ₃. Pero, ¿por qué ese pico es tan pequeño? nd ¿por qué la línea integral apenas se movía hacia arriba a medida que pasa sobre el pico? Si hay un H en CHCl ₃, ¿su integral debe coincidir con el 1H en etanol?

Volvamos al espectro del etanol y veamos algunas formas diferentes en las que podemos ver la integración. En ocasiones, la línea integral se corta en integrales separadas para cada pico para que puedan compararse entre sí más fácilmente.

Figura\(\PageIndex{2}\): Espectro de RMN ^1H de etanol con línea integral discontinua.

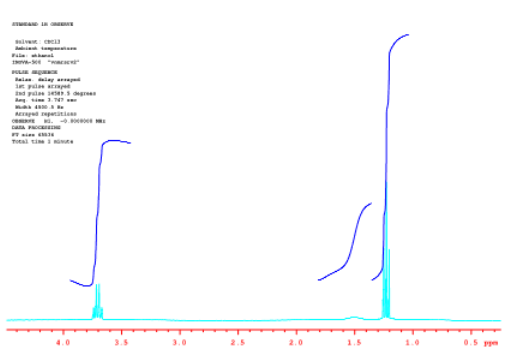
Fuente: Espectro tomado en CdCl ₃ en un Espectrómetro Varian Gemini 2000 con imán Oxford de 300 MHz.

En la imagen de arriba, es más fácil ver la relación 2:1:3 entre los picos.

A menudo, en lugar de mostrar datos brutos, las integrales se miden y sus alturas se muestran en el espectro.

Figura\(\PageIndex{3}\): Espectro de RMN ^1H de etanol con integrales numéricas.

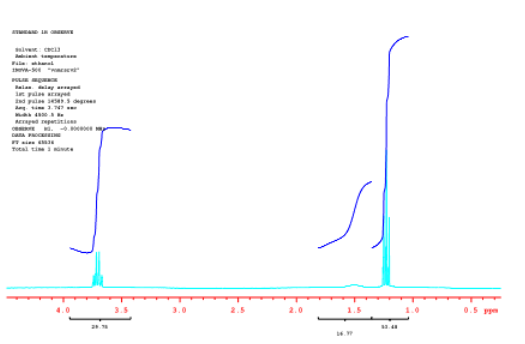
Fuente: Espectro tomado en CdCl ₃ en un Espectrómetro Varian Gemini 2000 con imán Oxford de 300 MHz.

Los números bajo el espectro leían, de izquierda a derecha, 29.76, luego 14.99 y finalmente 53.48. Aproximadamente, estos números son 30:15:54. Eso es cercano a una relación 2:1:3, aunque 30:15:45 sería un ajuste aún mejor. Tenga en cuenta que la impresión numérica que obtenemos no coincide exactamente con la relación que esperamos; de hecho, parece un poco peor que la relación que estimamos aproximadamente a simple vista. Eso es porque realmente es peor que la proporción que medimos aproximadamente a ojo.

Cuando comparaste las integrales a simple vista, estabas mirando una línea integral azul completa y comparándola con otra línea integral azul completa. Estabas realizando lo que se llama “análisis mulivariable”. Cada línea integral está compuesta por docenas o cientos de puntos de datos. Tu cerebro toma toda esa información y la pesa cuidadosamente para llegar a una idea de cuán altos son los pasos integrales a medida que pasa por un pico.

Es difícil encontrar un software de RMN que realice este análisis de la mejor manera posible. Puede llegar a números mucho más precisos de lo que puedas, pero sus números son menos confiables que los tuyos. Eso es porque la computadora solo está haciendo un análisis de dos puntos de datos; mide el cambio en la coordenada y desde el inicio de la línea azul hasta el final de la línea azul. Sigue siendo útil, pero ten en cuenta que no va a estar muerto, sobre todo si los extremos de la línea integral están inclinados.

A veces las alturas se “normalizan”. Se reducen a un factor común más bajo para que sus proporciones sean más fáciles de comparar. Estos números podrían corresponder a números de hidrógenos, o simplemente a sus factores comunes más bajos. Dos picos en una relación de 1H:2H podrían corresponder a uno y dos hidrógenos, o podrían corresponder a dos y cuatro hidrógenos, etc.

Figura\(\PageIndex{4}\): Espectro de RMN ^1H de etanol con números integrales normalizados.

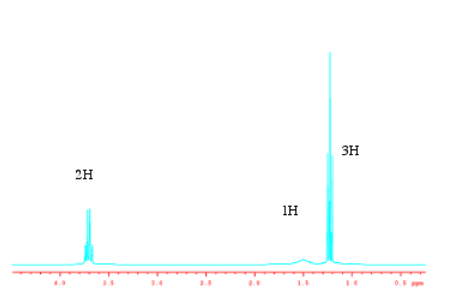
Fuente: Espectro tomado en CdCl ₃ en un Espectrómetro Varian Gemini 2000 con imán Oxford de 300 MHz.

Tenga en cuenta que la relación no se parece en nada a una comparación de las alturas de los picos. Si solo tuviéramos que estimar las alturas de los picos, podríamos llegar a algo así como 1:0. 1:3 o 10:1:30. Las integrales están midiendo el área total del pico, por lo que el ancho del pico importa así como su altura.

Ejercicio\(\PageIndex{1}\)

Debido a que el espectro de RMN 1H tiene una resolución relativamente baja, los espectros de hidrocarburos saturados de cadena lineal son todos similares: un pico para los hidrógenos de metilo a 0.9 ppm y un pico para los hidrógenos de metileno (CH ₂) a 1.0 ppm. Sin embargo, diferentes hidrocarburos pueden ser identificados por sus valores de integración.

Predecir las integraciones para los siguientes compuestos:

a) pentano b) octano c) decano d) heptano e) hexano

Responder

a) 0.9 ppm, 6H; 1.0 ppm, 6H (relación 1:1)

b) 0.9 ppm, 6H; 1.0 ppm, 12H (relación 1:2)

c) 0.9 ppm, 6H; 1.0 ppm, 16H (relación 3:8)

d) 0.9 ppm, 6H; 1.0 ppm, 10H (relación 3:5)

e) 0.9 ppm, 6H; 1.0 ppm, 8H (relación 3:4)

Ejercicio\(\PageIndex{2}\)

Dibuje un espectro de RMN predicho para cada uno de los siguientes compuestos, con una línea integral sobre cada pico.

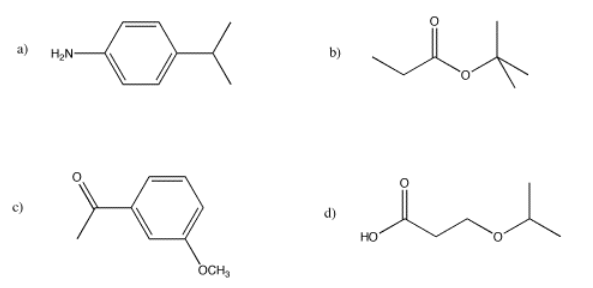
Responder

a)

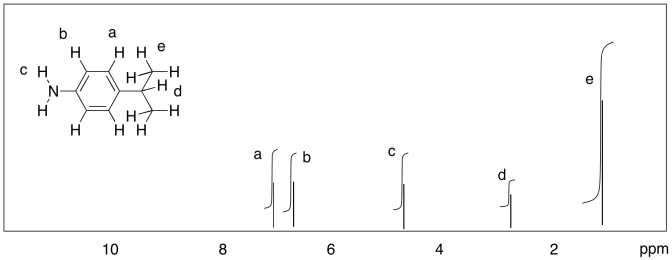
b)

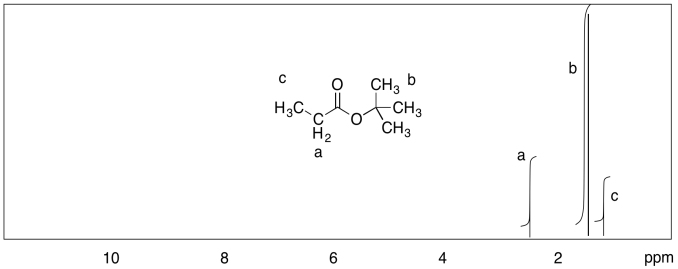
c)

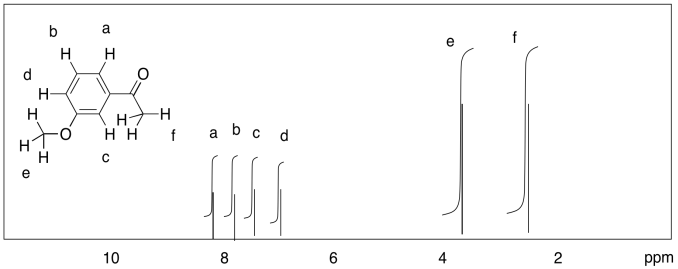
d)

Ejercicio\(\PageIndex{3}\)

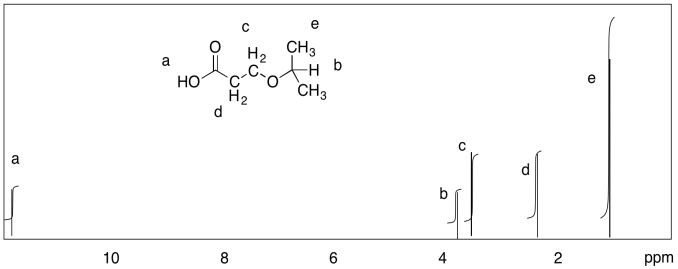
Mida las integrales en los siguientes compuestos. Dadas las proporciones integrales y los cambios químicos, ¿puedes hacer coincidir cada pico con un conjunto de protones?

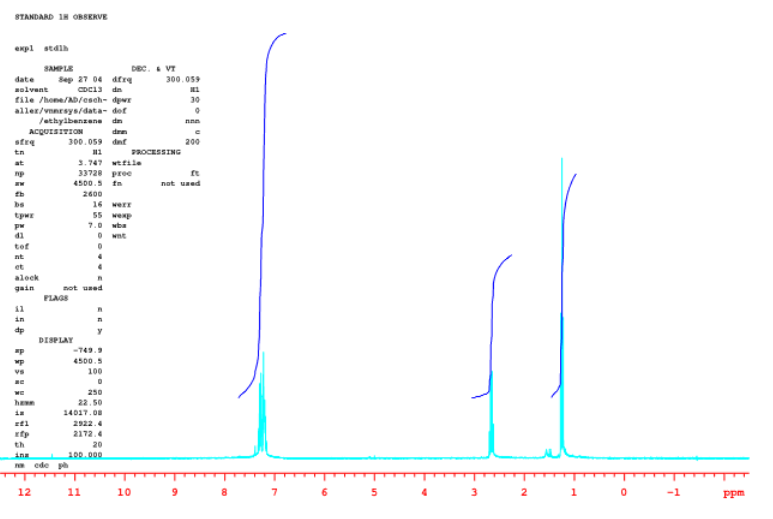
Responder

a) 5:2:3