4.11: Acoplamiento más complicado

Última actualización
Guardar como PDF

Page ID: 79122

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

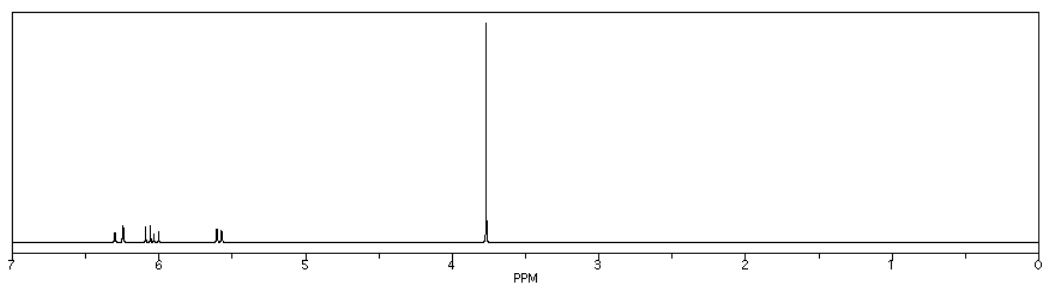
La regla n + 1 (número de líneas en un multiplete = número de H + 1 vecinos) funcionará para la mayoría de los problemas que pueda encontrar. Ocasionalmente, es posible que veas un acoplamiento más complicado. El espectro del acrilato de metilo es un buen ejemplo. Hay un par de puntos a anotar en este espectro, comenzando por el número de picos.

Figura\(\PageIndex{1}\): Espectro de RMN ^1H de acrilato de metilo.

Fuente: Espectro simulado.

la porción vinílica del espectro (hidrógenos adyacentes al doble enlace C=C) muestra tres picos, no solo dos.
aunque hay dos protones en un carbono vinílico, cada H es diferente debido a las relaciones cis/trans: uno H es cis al carbonilo y el otro es trans a él.
estos hidrógenos son simetría inequivalente.

Además, existe un problema con el acoplamiento en la región vinílica.

el protón adyacente al carbonilo, a 6 ppm, tiene dos vecinos y debe dar un triplete.
en cambio, el pico de este protón muestra cuatro líneas, no tres.
este pico no es un cuarteto; los dos picos medios no son tres veces más altos que los de borde.
las líneas dentro de este multiplete están simétricamente espaciadas, pero no uniformemente; el espacio medio es más pequeño que los espacios en los bordes.

A este patrón se le llama “doblete de dobletes”. Los dos vecinos de simetría-inequivalente en el otro extremo del doble enlace actúan cada uno como si el otro no estuviera ahí. Se acoplan al protón junto al carbonilo independientemente, dividiendo cada uno el pico para este protón en un doblete separado.

Hay algunos casos en los que este acoplamiento independiente ocurrirá en lugar del acoplamiento de tipo (n+1) que vimos primero. Generalmente, el acoplamiento independiente ocurre cuando los protones no giran libremente. Eso puede suceder si uno de los protones está unido a un carbono de doble enlace, porque no podemos rotar alrededor de un doble enlace. También puede ocurrir con protones que están directamente unidos a los carbonos de un anillo.

Para ver por qué sucede esto, necesitas saber más sobre el acoplamiento.

en acoplamiento, la información magnética se comparte entre dos protones. Cuán completamente se comparte esta información depende del ángulo entre los hidrógenos a medida que mira hacia abajo el enlace C-C de conexión.
para el acoplamiento (n+1), el ángulo de rotación alrededor del enlace C-C que conecta los dos protones (o 'ángulo diédrico' entre los hidrógenos acoplados) debe ser irrestricto. El enlace debe poder rotar libremente.
si el enlace puede girar libremente, cualquier protón en el carbono vecino puede asumir cualquier ángulo diedro con el protón siendo observado. Eso significa que la información de acoplamiento de un protón vecino es indistinguible de otro, por lo que todos los protones vecinos afectan al protón observado por igual.

Figura\(\PageIndex{2}\): Proyección de corzo (arriba) y proyección Newman de etanol (abajo), mostrando la relación angular entre hidrógenos en carbonos vecinos. El ángulo entre dos grupos en los carbonos vecinos se denomina ángulo diedro. Debido a la libre rotación alrededor del enlace C-C, los tres hidrógenos en el metilo tienen una relación espacial equivalente a los hidrógenos en el grupo CH ₂.

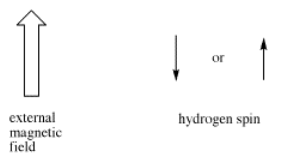
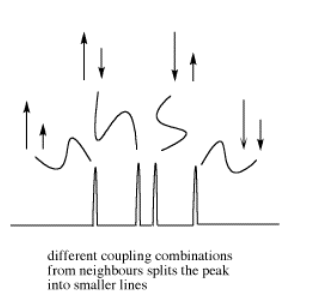
A veces, la información de acoplamiento se representa como una flecha. Esta flecha representa la constante de acoplamiento entre dos protones. La constante de acoplamiento está relacionada con el espín de un átomo de hidrógeno. El giro (relacionado con el momento magnético) puede alinearse con el campo magnético externo (lo mostraremos apuntando hacia arriba) o bien contra él; no se permiten otras posibilidades.

Si hay dos hidrógenos vecinos, ambos espines podrían estar alineados con el campo externo, ambos podrían estar alineados contra él, o uno podría estar alineado en cada sentido. Eso significa que hay tres combinaciones magnéticas diferentes que tendrán cada una un efecto diferente sobre el protón observado: aumento del campo magnético, disminución del campo magnético y ningún efecto neto (cancelación).

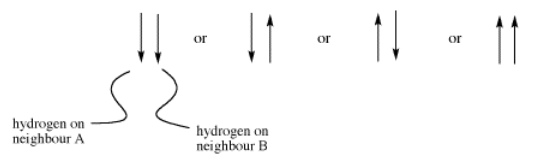
Estas tres combinaciones dan como resultado que el protón observado absorba a tres frecuencias diferentes, ya que la frecuencia que absorbe es sensible al campo magnético que experimenta. Tenga en cuenta que hay dos formas de llegar a la posibilidad media, con un vecino spin up y el otro spin down. Estadísticamente, esta posibilidad es el doble de probable que ambos giros hacia arriba o ambos giros hacia abajo. Por lo tanto, es dos veces más probable que el protón observado experimente ese efecto, y así la línea media en un triplete es dos veces más alta que las otras dos líneas.

Figura\(\PageIndex{3}\): Efectos de protones vecinos sobre un pico observado. Este caso supone que todos los protones vecinos tienen un efecto equivalente (tienen la misma constante de acoplamiento con el protón observado).

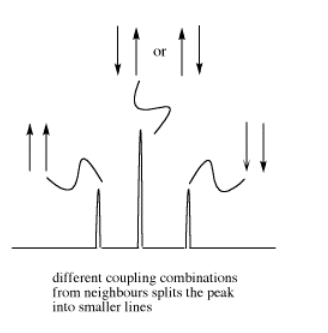
Sin embargo, el tamaño de esa flecha, la constante de acoplamiento, es solo el mismo para dos hidrógenos vecinos si tienen la misma relación espacial con el hidrógeno observado. Eso no siempre es cierto.

si el ángulo diedro es limitado, se produce un acoplamiento complejo.
el acoplamiento complejo ocurre porque un hidrógeno vecino solo puede adoptar un rango limitado de ángulos diedros. Otro protón vecino también puede adoptar un rango limitado de ángulos diedros, pero estos dos rangos no se superponen.

Como resultado, las dos constantes de acoplamiento son diferentes. Podemos representar esa situación usando flechas de diferentes longitudes para los dos giros de protones vecinos. Cada giro puede ser hacia arriba o hacia abajo, pero ahora dos giros opuestos no se cancelan. El resultado son cuatro combinaciones de giro de igual probabilidad, no sólo tres.

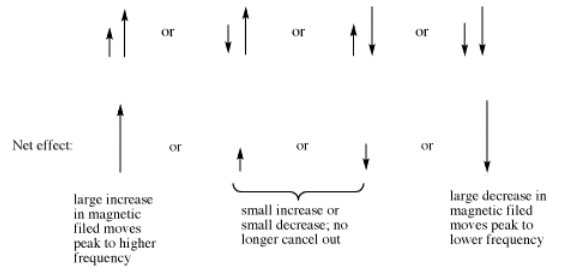
El doblete de dobletes es de cuatro líneas de alturas aproximadamente iguales. La distancia entre los dos pares de líneas en cada borde

Figura\(\PageIndex{4}\): Efectos de protones vecinos sobre un pico observado. Este caso asume que los protones vecinos tienen efectos inequivalentes (tienen diferentes constantes de acoplamiento con el protón observado).

El ángulo diedro está limitado en solo unos pocos casos específicos:

hay un doble enlace. Los dobles enlaces no pueden rotar porque eso requeriría romper el enlace pi. En un enlace pi, los orbitales p en los dos carbonos deben permanecer coplanares para superponerse y formar un enlace.
hay un anillo. En un anillo, no puede haber una rotación completa alrededor de un enlace porque el anillo se torcería en un pretzel.
en algunos casos, puede haber grupos tan grandes de átomos en cada extremo de un enlace que es difícil rotar el enlace sin que estos grupos choquen entre sí.

Ejercicio\(\PageIndex{1}\)

Espectros de bosquejo para los siguientes compuestos.

a) alcohol alílico o 2-propeno-1-ol, HOCH ₂ CH=CH ₂

b) estireno o vinilbenceno, C ₆ H ₅ CH=CH ₂

c) trans-1-cloropropeno, CH ₃ CH=CHCl

Ejercicio\(\PageIndex{2}\)

Se demostró que un compuesto por espectrometría de masas de alta resolución tenía la fórmula probable C ₆ H ₁₀ O ₂.

a) ¿Cuál es el grado de saturación en este compoud?

b) La espectroscopia IR dio los siguientes datos: 3105 (w), 2950 (m), 1517 (m), 1235 (s), 1056 (s), 715 (m) cm ^-1. Proporcione una tabla de datos con posibles asignaciones para estos picos.

c) La espectroscopía de RMN ^1H proporcionó el siguiente espectro. Proporcionar una tabla de datos con estructuras parciales para cada pico.

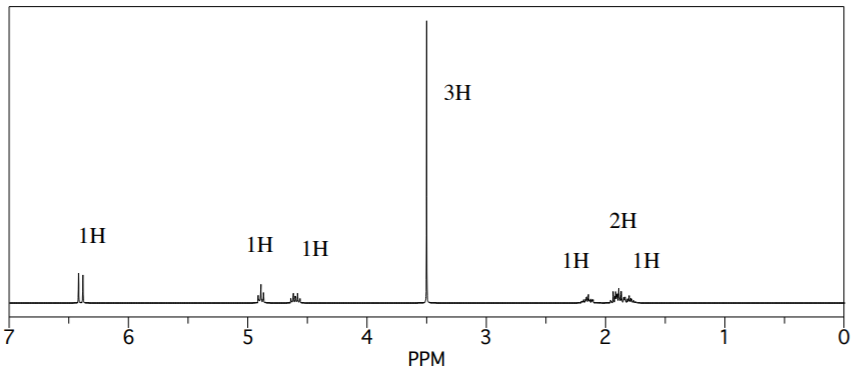
d) Sugerir una estructura probable para este compuesto

Ejercicio\(\PageIndex{3}\)

Se demostró que un compuesto por espectrometría de masas de alta resolución tenía la fórmula probable C ₅ H ₈ O ₂.

¿Cuál es el grado de saturación en este compuesto?
La espectroscopia IR dio los siguientes datos: 2950 (m), 2825 (m), 2716 (m), 1724 (s), 1505 (m), 1056 (w) cm ^-1. Proporcione una tabla de datos con posibles asignaciones para estos picos.
La espectroscopía de RMN ^1H proporcionó el siguiente espectro. Proporcionar una tabla de datos con estructuras parciales para cada pico.
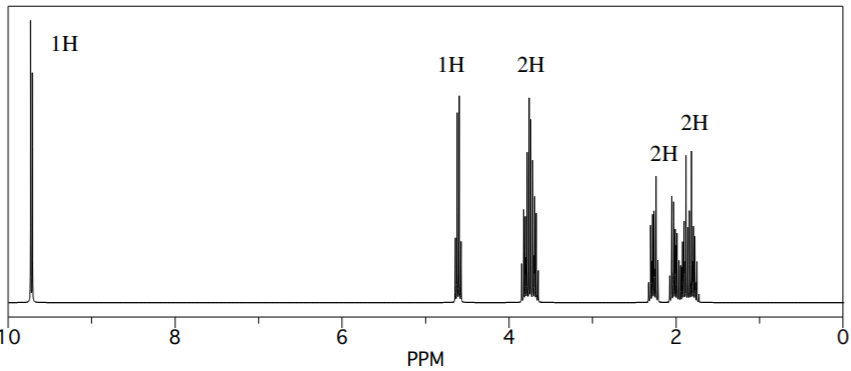
Sugerir una estructura probable para este compuesto.

Ejercicio\(\PageIndex{4}\)

Se aisló una muestra de un producto natural de material vegetal y se sometió a análisis.

La espectroscopia IR dio los siguientes datos: 3097 (m), 2975 (m), 1600 (m), 1495 (m), 1235 (s), 1056 (s), 747 (m), 705 (m) cm ^-1. Proporcione una tabla de datos con posibles asignaciones para estos picos.
Se demostró que el compuesto por espectrometría de masas de alta resolución tenía la fórmula probable C ₁₀ H ₁₂ O. ¿Cuál es el grado de insaturación en este compuesto?
La espectroscopía de RMN ^1H proporcionó el siguiente espectro. Proporcionar una tabla de datos con estructuras parciales para cada pico.
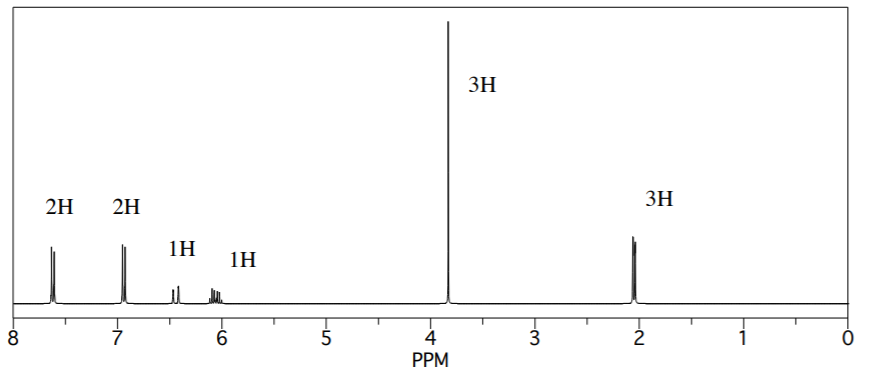
Sugerir una estructura probable para este compuesto.