6.26: Difusión en Estado Constante, Coeficiente de Difusión, Segunda Ley de Fick

Difusión en estado estacionario

La difusión se refiere al movimiento neto de una especie por un gradiente de concentración, de un área de alta concentración a un área de baja concentración. Es importante destacar que la difusión puede tener lugar en cualquier fase de la materia, ¡incluso en sólidos! La difusión en estado estacionario (independiente del tiempo) es descrita por la primera ley de Fick:

$J=-D \dfrac{d C}{d x}$

Aquí,$\mathrm{J}$ está el flujo de difusión: la velocidad a la que una cantidad de una sustancia pasa a través de un área superficial. El flujo de difusión tiene unidades de$\frac{\text { amount }}{\text { areaxtime }}$, o$\frac{\mathrm{mol}}{\mathrm{m}^2 s}$. $\mathrm{D}$es el coeficiente de difusión, que a veces se llama difusividad. Depende de las circunstancias específicas en las que se esté produciendo la difusión, incluyendo qué materiales están involucrados y el estado del entorno circundante. Cuenta con unidades de$\frac{m^2}{s}$. Finalmente, aquí$\mathrm{C}$ está la concentración ($M$o$\frac{\mathrm{mol}}{\text { volume }}$, también lo$\frac{d C}{d x}$ es el cambio en la concentración con respecto al cambio de posición. Por lo tanto, la primera ley de Fick nos dice cómo el cambio de concentración fluye sobre la región entre dos concentraciones diferentes.

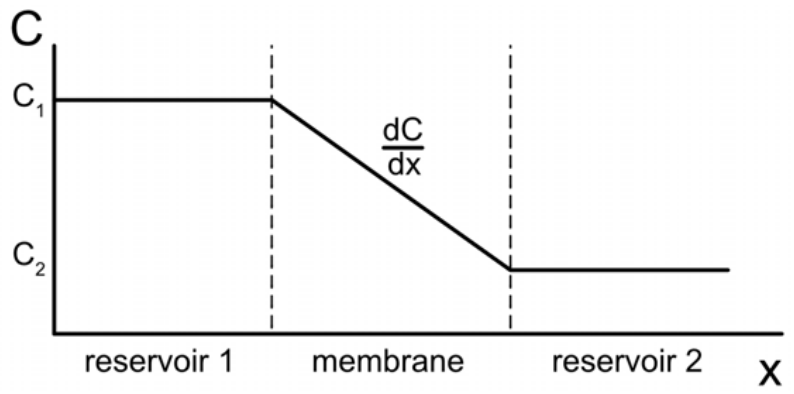
Ejemplo: Si calientas acero en una atmósfera rica en carbono, los átomos de carbono se difundirán en el acero, endureciéndolo. Calcular la difusividad de una placa de acero si el flujo de átomos de carbono a través de la placa es$2 \times 10^{-6} \frac{g}{m^2 s}$, la concentración$2 \mathrm{~mm}$ bajo la superficie es$300 \frac{g}{m^3}$, y la concentración$5 \mathrm{~mm}$ debajo de la superficie es$100 \frac{g^3}{m^3}$.

Contestar

Podemos reorganizar la primera ley de Fick y conectar:

\ begin {reunió}
D=-J\ izquierda (\ dfrac {d C} {d x}\ derecha) ^ {-1} =-J\ izquierda (\ dfrac {x_2-x_1} {C_2-C_1}\ derecha) =-2\ veces 10^ {-6}\ dfrac {g} {m^2 s}\ izquierda (\ dfrac {\ izquierda (2\ tiempos 10^ {-3} -5\ veces 10^ {-3}\ derecha) m} {\ izquierda (3\ veces 10^2-1\ veces 10^2\ derecha)\ frac {g} {m^3}}\ derecha)\\
D=3\ veces 10^ {- 11}\ dfrac {m^2} {\ mathrm {~s}}
\ final {reunidos}

Donde hemos aproximado el gradiente de concentración como lineal.

Coeficiente de difusión

La difusión es un proceso activado térmicamente y la dependencia de la temperatura se refleja en el coeficiente de difusión. El coeficiente de difusión (difusividad) también es descrito por una relación Arrhenius! Imagínese un átomo que se difunde a través de un sólido cristalino: tiene que moverse a través de la celosía. Una forma en que esto puede suceder es, si el átomo es suficientemente pequeño, puede viajar lúpulo de sitio intersticial a sitio intersticial. Los átomos más grandes también pueden difunderse, pero es un proceso que consume más energía. Un mecanismo para que esto suceda es si primero se crea una vacante en la red, y luego el átomo difusor se mueve hacia el sitio de la red ahora vacante. A medida que las vacantes se difunden a través de la red, otras especies pueden seguir. Por supuesto, hay más partes móviles con este proceso, y se requiere más energía.

La energía requerida para que ocurra la difusión puede considerarse como una energía de activación. El coeficiente de difusión es

$D=D_0 e^{-\dfrac{E_a}{k_B T}}$

Aquí,$D_0$ es el valor máximo de difusividad,$E_a$ es la energía de activación,$k_B$ es la constante de Boltzmann, y$T$ es la temperatura. Al describir el coeficiente de difusión con una relación Arrhenius, recordemos que estamos diciendo que a una temperatura dada$T$,, la relación de la energía térmica dada por$k_B T$ a la energía de activación$E_a$ establece el valor del coeficiente de difusión, y se maximiza a temperatura infinita .

Segunda ley de Fick

Si el perfil de concentración varía con respecto al tiempo, la suposición de estado estacionario ya no se mantiene, y en su lugar se usa la segunda ley de Fick:

$\dfrac{\partial C}{\partial t}=D \dfrac{\partial^2 C}{\partial x^2}$

Las soluciones a la segunda ley de Fick son de la forma

$\dfrac{C(x, t)-C_0}{C_s-C_0}=1-\operatorname{erf}\left(\dfrac{x}{2 \sqrt{D t}}\right)$

Aquí,$C_s$ es la concentración de la fuente,$C_0$ es la concentración inicial,$C(x, t)$ es la expresión para la concentración en función de la posición y el tiempo,$\mathrm{D}$ es el coeficiente de difusión, y erf es la función de error.