2.2: Construcción de orbitales moleculares a partir de orbitales atómicos

La teoría orbital molecular implica resolver (aproximadamente) la ecuación de Schrödinger para los electrones en una molécula. Para revisar desde el Capítulo 1, se trata de una ecuación diferencial en la que los términos primero y segundo a la derecha representan las energías cinética y potencial:

\[E \psi = -\frac{\hbar^{2}}{2\mu} \nabla^{2} \psi + V \psi\]

Si bien la ecuación de Schrödinger puede resolverse analíticamente para el átomo de hidrógeno, la función de energía potencial V se vuelve más complicada -y la ecuación solo puede resolverse numéricamente- cuando hay muchos electrones (mutuamente repulsivos) en una molécula. Entonces como primera aproximación asumiremos que los orbitales s, p, d, f, etc. de los átomos que componen la molécula son buenas soluciones a la ecuación de Schrödinger. Entonces podemos permitir que estas funciones de onda interfieran constructiva y destructivamente a medida que juntamos los átomos para hacer enlaces. De esta manera, utilizamos los orbitales atómicos (AO) como base para construir MO.

LCAO-MO = combinación lineal de orbitales atómicos. En física, esto se llama a esto la aproximación de unión apretada.

De hecho, hemos visto combinaciones lineales de orbitales atómicos antes cuando construimos orbitales híbridos en el Capítulo 1. Las reglas básicas que desarrollamos para la hibridación también se aplican aquí: los orbitales se agregan con coeficientes escalares (c) de tal manera que los orbitales resultantes son ortogonales y normalizados. La diferencia es que en el caso MO, los orbitales atómicos provienen de diferentes átomos.

La combinación lineal de orbitales atómicos siempre devuelve el mismo número de orbitales moleculares. Entonces, si comenzamos con dos orbitales atómicos (por ejemplo, un orbital s y un p _z como se muestra en la Fig. \(\PageIndex{1}\)), terminamos con dos orbitales moleculares. Cuando los orbitales atómicos se suman en fase, obtenemos interferencia constructiva y un orbital de menor energía. Cuando se suman fuera de fase, obtenemos un nodo y el orbital resultante tiene mayor energía. Los MO de menor energía se están uniendo y los MO de mayor energía son antiaglutinantes.

Figura\(\PageIndex{1}\): Combinaciones de unión sigma y antiunión de un orbital s y p

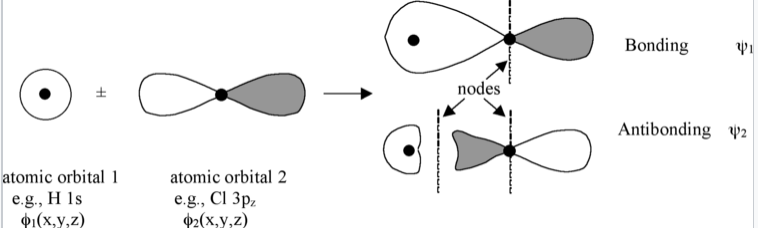
Los orbitales moleculares también se denominan funciones de onda (ψ), porque son soluciones a la ecuación de Schrödinger para la molécula. Los orbitales atómicos (también llamados funciones base) están etiquetados como φ, por ejemplo, φ _1s y φ _3pz o simplemente como φ ₁ y φ ₂.

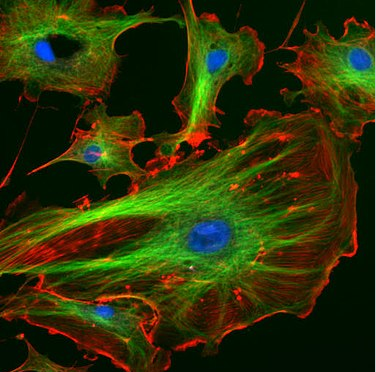
En principio, necesitamos resolver la ecuación de Schrödinger para todos los orbitales en una molécula, y luego llenarlos de pares de electrones como lo hacemos para los orbitales en átomos. En la práctica estamos realmente interesados sólo en los MO que derivan de los orbitales de valencia de los átomos constituyentes, porque estos son los orbitales que están involucrados en la unión. Estamos especialmente interesados en los orbitales fronterizos, es decir, el orbital molecular ocupado más alto (el HOMO) y el orbital molecular desocupado más bajo (el LUMO). Los orbitales llenos que son mucho más bajos en energía (es decir, orbitales centrales) no contribuyen a la unión, y los orbitales vacíos a mayor energía tampoco contribuyen. Sin embargo, esos orbitales son importantes en fotoquímica y espectroscopia, que implican transiciones electrónicas de orbitales ocupados a vacíos. Los colorantes fluorescentes que tiñen las células mostradas en la Fig. \(\PageIndex{2}\)absorber la luz promoviendo electrones en el HOMO para vaciar MO y emitir luz cuando los electrones descienden de nuevo a sus niveles de energía originales.

Figura\(\PageIndex{2}\): Los diferentes componentes de las células endoteliales se tiñen con colorantes fluorescentes azul, verde y rojo. Para cada colorante el color de la luz emitida corresponde a la energía emitida cuando un electrón cae del LUMO al HOMO de la molécula.

Como ejemplo del enfoque LCAO-MO podemos construir dos MO (ψ ₁ y ψ ₂) de la molécula de HCl a partir de dos AO φ ₁ y φ ₂ (Fig. 2.1.1). Para hacer estas dos combinaciones lineales, escribimos:

\[\Psi_{1}=c_{1}\varphi_{1} + c_{2}\varphi_{2}\]

y

\[\Psi_{2}=c_{1}\varphi_{1} - c_{2}\varphi_{2}\]

Los coeficientes c ₁ y _c2 serán iguales (o casi así) cuando los dos AO a partir de los cuales se construyen son los mismos, por ejemplo, cuando dos orbitales de hidrógeno 1s se combinan para hacer MOs de enlace y antienlace en H ₂. Serán desiguales cuando haya una diferencia de energía entre los AO, por ejemplo cuando una orbital de hidrógeno 1s y una orbital de cloro 3p se combinan para hacer un enlace polar H-Cl.

Nodos:

Las funciones de onda φ y ψ son amplitudes que están relacionadas con la probabilidad de encontrar el electrón en algún punto del espacio. Tienen lóbulos con signos (+) o (-), los cuales indicamos por sombreado o color. Dondequiera que la función de onda cambie signo tenemos un nodo. Como se puede ver en la Fig. \(\PageIndex{1}\), los nodos en MO son el resultado de la interferencia destructiva de las funciones de onda (+) y (-). Generalmente, cuantos más nodos, mayor es la energía de la órbita.

En el ejemplo anterior hemos dibujado una imagen simplificada del orbital Cl 3p _z y los MOs resultantes, dejando fuera el nodo radial. Recordemos que los orbitales 2p no tienen nodos radiales, los orbitales 3p tienen uno, como se ilustra en la Fig. \(\PageIndex{3}\). Los orbitales 4p tienen dos nodos radiales, y así sucesivamente. Los MO que hacemos combinando los AO también tienen estos nodos.

Figura\(\PageIndex{3}\): Estructura nodal de orbitales 2p y 3p

Normalización:

Cuadramos las funciones de onda para obtener probabilidades, que siempre son positve o cero. Entonces, si un electrón está en orbital φ ₁, la probabilidad de encontrarlo en el punto xyz es el cuadrado ^[1] de φ ₁ (x, y, z). La probabilidad total no cambia cuando combinamos AO para hacer MOs, así que para el caso simple de combinar φ ₁ y φ ₂ para hacer ψ ₁ y ψ ₂,

\[\Psi_{1}^{2} + \Psi_{2}^{2} = \varphi_{1}^{2} + \varphi_{2}^{2}\]

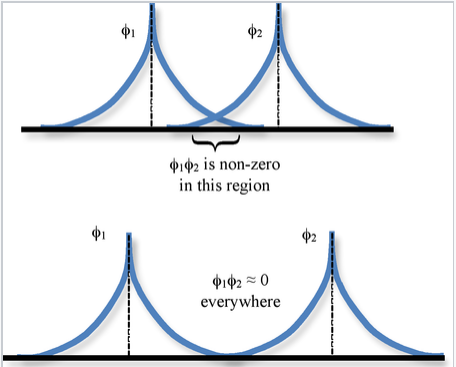
Integral de superposición:

El solapamiento espacial entre dos orbitales atómicos φ ₁ y φ ₂ se describe por la integral de superposición S,

\[S_{12} = \int \varphi_{1} * \varphi_{2} d\tau \]

donde la integración está en todo el espacio\(d\tau = dx dy dz\).

Figura\(\PageIndex{4}\): Las funciones de onda de los orbitales atómicos disminuyen exponencialmente con la distancia. El solapamiento orbital es distinto de cero cuando dos átomos están muy juntos, como se ilustra para los orbitales de 1s en la figura superior. La cifra inferior muestra orbitales que están demasiado lejos para interactuar. En este caso tanto S como β están cerca de cero.

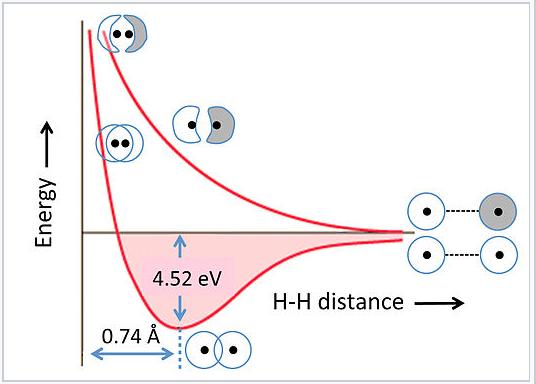
Energías de MoS de unión y antiadhesión:

Las energías de los orbitales enlazantes y antiligantes dependen fuertemente de la distancia entre los átomos. Esto se ilustra en la Fig. 2.1.5 para la molécula de hidrógeno, _H2. A distancias muy largas, esencialmente no hay diferencia de energía entre las combinaciones en fase y fuera de fase de los orbitales H 1s. A medida que se acercan, la combinación en fase (unión) disminuye de energía porque los electrones se comparten entre los dos núcleos cargados positivamente. La energía alcanza un mínimo a la distancia de enlace de equilibrio (0.74 Å) y luego vuelve a subir a medida que los núcleos se acercan. La combinación antiunión tiene un nodo entre los núcleos por lo que su energía aumenta continuamente a medida que los átomos se juntan.

Figura\(\PageIndex{5}\): Energía en función de la distancia para los orbitales de unión y antiunión de la molécula _H2

A la distancia de enlace de equilibrio, las energías de los orbitales moleculares de enlace y antiunión (ψ ₁, ψ ₂) son menores y mayores, respectivamente, que las energías de los orbitales de base atómica φ ₁ y φ ₂. Esto se muestra en la Fig. \(\PageIndex{6}\)para los MO de la molécula H ₂.

Figura\(\PageIndex{6}\): Diagrama de energía orbital molecular para la molécula _H2

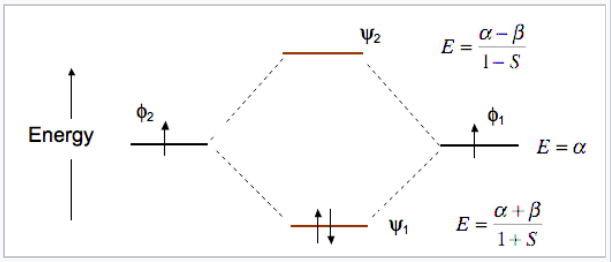
La energía de un electrón en uno de los orbitales atómicos es α, la integral Coulomb.

\[\alpha = \int \varphi_{1} H \varphi_{1}d\tau\]

donde H es el operador hamiltoniano. Esencialmente, α representa la energía de ionización de un electrón en orbital atómico φ ₁ o φ ₂.

La diferencia de energía entre un electrón en los AO y los MO está determinada por la integral de intercambio β,

\[\beta = \int \varphi_{1}H\varphi_{2}d\tau\]

β es una cantidad importante, porque nos habla de la energía de unión de la molécula, y también de la diferencia de energía entre orbitales ligantes y antiligantes. El cálculo de β no es sencillo para las moléculas de múltiples electrones porque no podemos resolver analíticamente la ecuación de Schrödinger para las funciones de onda. Sin embargo, podemos hacer algunas aproximaciones para calcular las energías y las funciones de onda numéricamente. En la aproximación de Hückel, que puede ser utilizada para obtener soluciones aproximadas para orbitales moleculares π en moléculas orgánicas, simplificamos la matemática tomando S=0 y estableciendo H=0 para cualquier orbitales p que no sean adyacentes entre sí. El método extendido de Hückel, ^[2] desarrollado por Roald Hoffmann, y otros métodos semiempíricos se pueden utilizar para obtener rápidamente energías orbitales relativas, funciones de onda aproximadas y degeneraciones de orbitales moleculares para una amplia variedad de moléculas y sólidos extendidos. Los métodos ab initio más sofisticados ahora están disponibles en paquetes de software y se pueden usar para calcular energías orbitales precisas para moléculas y sólidos.

Podemos obtener los coeficientes _c1 y _c2 para la molécula de hidrógeno aplicando el criterio de normalización:

\[\Phi_{1} = (\varphi_{1} + \varphi_{2})/(\sqrt{2(1+S)}) \textrm{(bonding orbital)}\]

y

\[\Phi_{2} = (\varphi_{1} - \varphi_{2})/(\sqrt{2(1-S)}) \textrm{(antibonding orbital)}\]

En el caso donde S≈0, podemos eliminar los términos 1-S y ambos coeficientes se convierten en 1/√2

Tenga en cuenta que el orbital de unión en el diagrama MO de H ₂ está estabilizado por una energía β/1+S y el orbital antiadhesión se desestabiliza por β/1-S. Es decir, el orbital antiadhesión sube en energía más de lo que baja el orbital de unión. Esto significa que H ₂ (ψ ₁ ² ψ ₂ ⁰) es energéticamente más estable que dos átomos de H, pero He ₂ con cuatro electrones (ψ ₁ ^{2 ψ 2 ₂}) es inestable en relación con dos átomos de He.

Orden de enlace: En cualquier diagrama MO, el orden de enlace se puede calcular como ½ (# de electrones de unión - # de electrones antiunión). Para H ₂ la orden de fianza es 1, y para He ₂ la orden de fianza es cero.

Caso heteronuclear (p. ej., HCl) - Enlaces polares

Aquí introducimos una diferencia de electronegatividad entre los dos átomos que forman el enlace químico. La energía de un electrón en el orbital H 1s es mayor (es más fácil de ionizar) que la del electrón en el orbital de cloro 3p _z. Esto da como resultado una mayor diferencia de energía entre los orbitales moleculares resultantes ψ ₁ y ψ ₂, como se muestra en la Fig. \(\PageIndex{7}\). Cuanto mayor es la diferencia de electronegatividad entre los orbitales atómicos (cuanto mayor es Δα), más “φ ₂ carácter” tiene el orbital de unión, es decir, más se parece al orbital Cl 3p _z en este caso. Esto es consistente con la idea de que H-Cl tiene un enlace sencillo polar: los dos electrones residen en un orbital molecular de enlace que se localiza principalmente en el átomo de Cl.

Figura\(\PageIndex{7}\): Diagrama de energía orbital molecular para la molécula de HCl

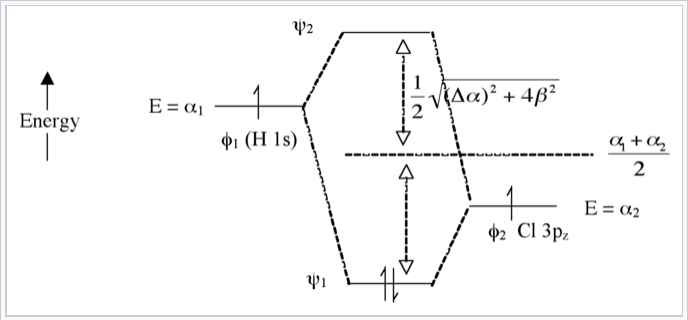
El orbital antiadhesión (vacío) tiene más carácter H. El orden de enlace es nuevamente 1 porque hay dos electrones en el orbital de unión y ninguno en el orbital antienlace.

Caso extremo - Unión iónica (NaF): Δα muy grande

En este caso, no hay mucha mezcla entre los AO porque sus energías están muy separadas (Fig. \(\PageIndex{8}\)). Los dos electrones de enlace están localizados en el átomo F, por lo que podemos escribir la molécula como Na ⁺ F ^-. Tenga en cuenta que si tuviéramos que excitar un electrón de ψ ₁ a ψ ₂ usando luz, la configuración electrónica resultante sería (ψ ₁ ¹ ψ ₂ ¹) y tendríamos Na ⁰ F ⁰. Esto se llama transición de transferencia de carga.

Figura\(\PageIndex{8}\): Diagrama de energía orbital molecular que ilustra la unión iónica en la molécula de NaF

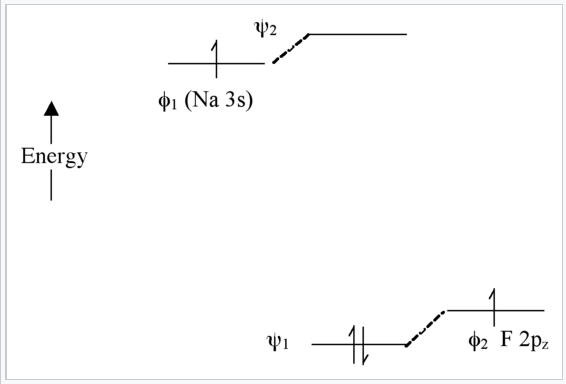
Resumen de la teoría orbital molecular hasta el momento:

• Sumar y restar funciones de onda AO para hacer MOs. Dos AO → dos MO. De manera más general, el número total de MO es igual al número de orbitales de base AO.

• Mostramos el caso más simple (sólo dos orbitales básicos). Los cálculos más precisos utilizan un conjunto de bases mucho mayor (más AO) y resuelven para la matriz de c's que da la energía total más baja, utilizando aproximaciones matemáticamente amigables de la función de energía potencial que forma parte del operador hamiltoniano H.

• Más nodos → MO de mayor energía

• Orden de enlace = ½ (# de electrones de unión - # de electrones antiunión)

• La polaridad del enlace emerge en la imagen MO como “carácter” orbital.

• Los AO que están muy separados en energía no interactúan mucho cuando se combinan para hacer MOs.