2.6: Llenado orbital

Los MO se llenan desde abajo según el principio de Aufbau y la regla de Hund, como aprendimos para los orbitales atómicos.

Pregunta: ¿cuál es la base mecánica cuántica de la regla de Hund?

Consideremos el caso de dos orbitales degenerados, como los orbitales π o π* en una molécula diatómica de segunda fila. Si cada uno de estos orbitales contiene un electrón, sus espines pueden ser paralelos (como lo prefiere la regla de Hund) o antiparalelos. El principio de exclusión Pauli dice que no hay dos electrones en un orbital que puedan tener el mismo conjunto de números cuánticos (n, l, m _l, m _s). Eso quiere decir que, en el caso paralelo, el principio Pauli impide que los electrones se visiten alguna vez los orbitales de los demás. En el caso antiparalelo, son libres de ir y venir porque tienen diferentes números cuánticos de m _s. Sin embargo, tener dos electrones en un mismo orbital es energéticamente desfavorable porque cargas similares se repelen. Así, el arreglo paralelo, gracias al principio Pauli, tiene menor energía.

Para O ₂ (12 electrones de valencia), obtenemos el diagrama de energía MO a continuación. Las formas de los orbitales moleculares se muestran a la derecha.

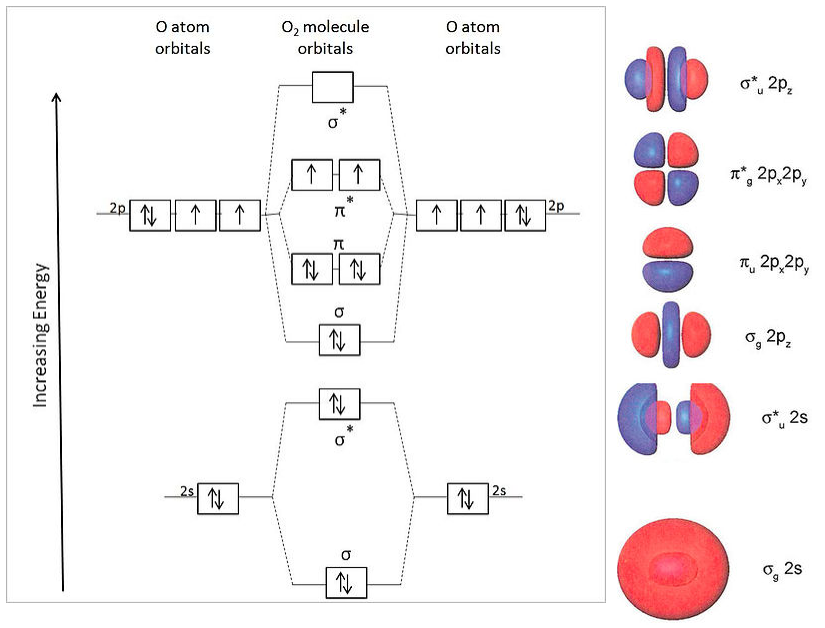
Este orden de energía de los MOS predice correctamente dos electrones desapareados en el orbital π* y un orden de enlace neto de dos (8 electrones de unión y 4 electrones antiunión). Esto es consistente con el paramagnetismo observado experimentalmente de la molécula de oxígeno.

Otras predicciones interesantes de la teoría MO para diatómicas de segunda fila son que la molécula C ₂ tiene un orden de enlace de 2 y que la molécula B ₂ tiene dos electrones desapareados (ambos verificados experimentalmente).

También podemos predecir (usando el diagrama O ₂, F ₂, Ne ₂ anterior) que NO tiene un orden de enlace de 2.5, y CO tiene un orden de bonos de 3.

Los símbolos “g” y “u” en las etiquetas orbitales, que solo incluimos en el caso de las moléculas centrosimétricas, se refieren a su simetría con respecto a la inversión. Los orbitales de Gerade (g) son simétricos, lo que significa que la inversión a través del centro deja la órbita sin cambios. Ungerade (u) significa que el signo de la órbita es revertido por la operación de inversión. Debido a que los orbitales g y u tienen simetrías diferentes, tienen cero solapamiento entre sí. Como veremos a continuación, factorizar orbitales según la simetría g y u simplifica la tarea de construir orbitales moleculares en moléculas más complicadas, como el butadieno y el benceno.

Las formas orbitales mostradas anteriormente se calcularon utilizando un modelo de un electrón de la molécula, como lo hicimos para los AO similares a hidrógeno para obtener las formas de orbitales s, p y d. Para obtener energías MO precisas y diagramas para moléculas de múltiples electrones (es decir, todas las moléculas reales), debemos incluir el hecho de que los electrones están “correlacionados”, es decir, que se evitan entre sí en las moléculas debido a su carga negativa. Este problema no se puede resolver analíticamente, y se resuelve aproximadamente en cálculos numéricos mediante el uso de la teoría funcional de la densidad (DFT). Aprenderemos sobre las consecuencias de la correlación electrónica en sólidos (como los superconductores) en el Capítulo 10.

Las estrellas gigantes rojas se caracterizan por la presencia de moléculas C 2 en sus atmósferas. Dado que C 2 tiene un orden de enlace neto de dos, reacciona rápidamente a medida que se enfría de la fase gaseosa para hacer otras formas de carbono como fullerenos, grafito y diamante, todos los cuales tienen cuatro enlaces por cada dos átomos de carbono.