2.8: Unión de tres centros

Muchos (pero no todos) de los problemas que resolveremos con la teoría MO derivan del diagrama MO de la molécula H ₂ (Fig. 2.1.5), que es un caso de unión de dos centros. El resto lo resolveremos por analogía al ion H ₃ ⁺, que introduce el concepto de unión de tres centros.

Podemos dibujar el ion H ₃ ⁺ (y también H ₃ y H ₃ ^-) en una geometría lineal o triangular.

Diagrama de correlación de Walsh para H ₃ ⁺:

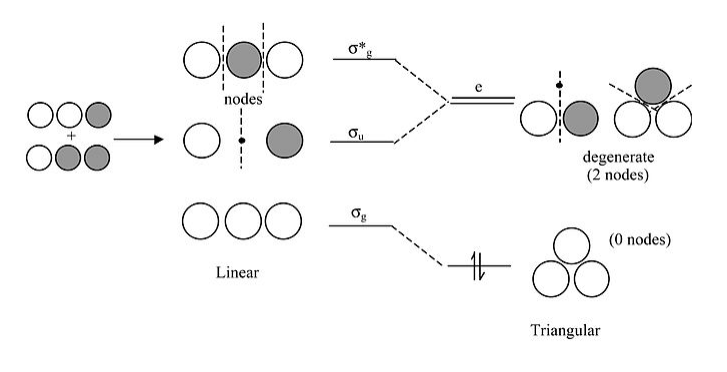
Algunos puntos importantes sobre este diagrama:

• Para la forma lineal del ion, los MO más altos y más bajos son simétricos con respecto al centro de inversión en la molécula. Tenga en cuenta que el orbital central 1s tiene simetría g, por lo que por simetría tiene superposición cero con la combinación u de los dos orbitales 1s en los extremos. Esto hace que el σ _u orbital sea un orbital no ligado.

• En la forma triangular de la molécula, los orbitales que derivan de σ _u y σ* _g se degeneran (es decir, tienen idénticamente la misma energía por simetría). El término símbolo “e” significa doblemente degenerado. Veremos más adelante que “t” significa triplicamente degenerado. Tenga en cuenta que dejamos caer la “g” y la “u” para los orbitales triangulares porque un triángulo no tiene un centro de inversión.

• La forma triangular es más estable porque los dos electrones en H ₃ ⁺ tienen menor energía en el orbital más bajo. Doblar la molécula crea una tercera interacción de unión entre los orbitales 1s en los extremos.

Diagrama MO para XH ₂ (X = Be, B, C...):

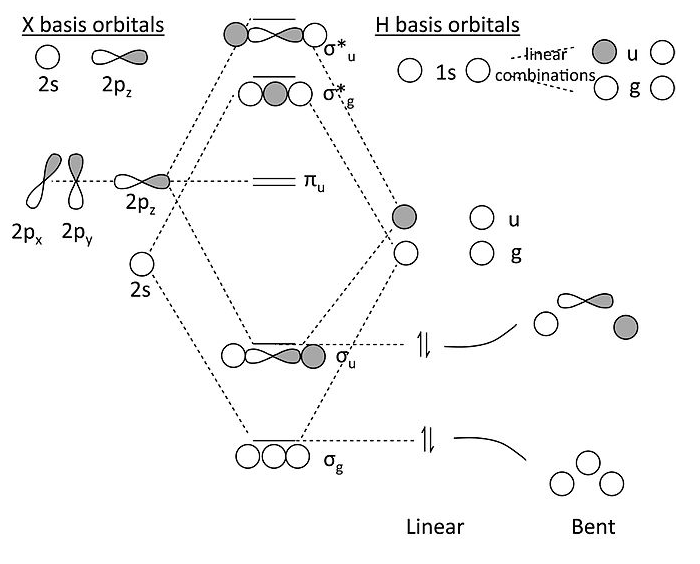
Algunos puntos clave sobre este diagrama MO:

• En la forma lineal de la molécula, que tiene simetría de inversión, los orbitales 2s y 2p del factor átomo X en tres clases de simetría:

2s = σ _g

2p _z = σ _u

2p _x, 2p _y = π _u

• De igual manera, podemos ver que los dos orbitales H 1s hacen dos combinaciones lineales, una con simetría σ _g y otra con simetría σ _u. Parecen los MO de unión y antiunión de la molécula H ₂ (por eso decimos que usamos ese problema para resolver este).

• Los orbitales π _u deben ser no vinculantes porque no hay una combinación de los orbitales H 1s que tenga simetría π _u.

• En el diagrama MO, hacemos combinaciones de unión y antiunión de las σ _g's y σ _u's. Para BeH ₂, luego poblamos los dos orbitales más bajos con los cuatro electrones de valencia y descubrimos (no es sorprendente) que la molécula tiene dos enlaces y puede escribirse H-Be-H. El diagrama de correlación muestra que una forma doblada de la molécula debe ser menos estable.

Una historia interesante sobre este diagrama MO es que es difícil predecir a priori si CH ₂ debe ser lineal o doblado. En 1970, Charles Bender y Henry Schaefer, utilizando cálculos químicos cuánticos, predijeron que el estado fundamental debería ser un triplete doblado con un ángulo H-C-H de 135°. ^[4] Los mejores experimentos en ese momento sugirieron que el metileno era un singlete lineal, y los teóricos argumentaron que el resultado experimental era incorrecto. ¡Experimentos posteriores demostraron que tenían razón!

“Una teoría es algo que nadie cree, excepto la persona que la hizo. Un experimento es algo que todos creen, excepto la persona que lo hizo”. — Einstein