5.3: Electrolitos
( \newcommand{\kernel}{\mathrm{null}\,}\)
¿Qué es un electrolito?
La corriente eléctrica se define como el movimiento de las cargas eléctricas. Las sustancias a través de las cuales puede fluir una corriente eléctrica se denominan conductores eléctricos, y las otras son no conductores eléctricos. Los metales son conductores eléctricos porque los electrones de valencia de los átomos metálicos pueden moverse en una pieza de metal. Los compuestos iónicos están compuestos por cationes y aniones, pero los iones en un sólido no pueden moverse. Por lo tanto, los compuestos iónicos sólidos son no conductores eléctricos. El agua pura no tiene una concentración suficiente de iones en ella y es un no conductor eléctrico. Los compuestos iónicos se disocian en iones cuando se disuelven en agua. La solución de compuestos iónicos en agua es un conductor eléctrico debido a que los iones pueden moverse en la solución, como se ilustra en la Fig. 5.3.1.
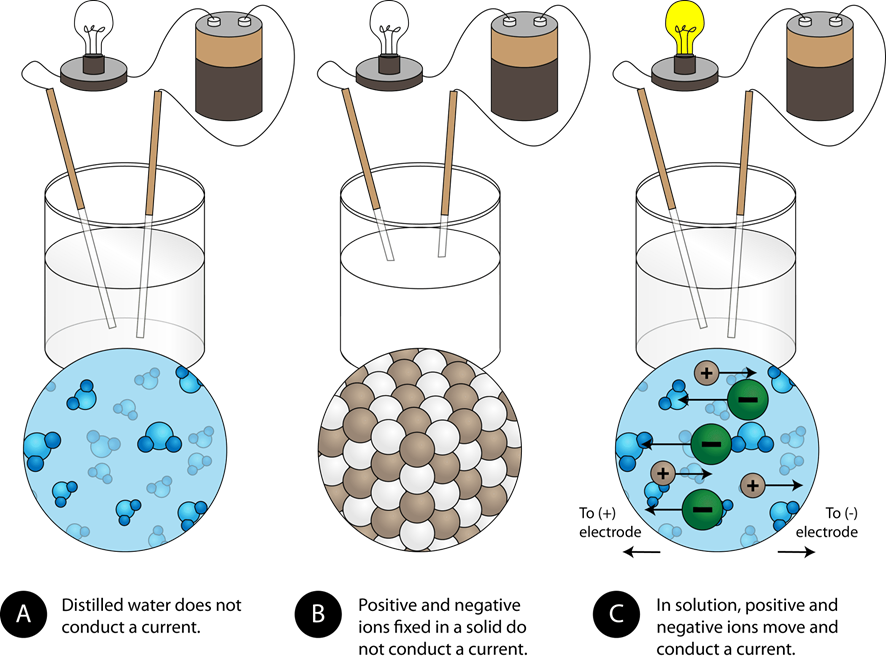
Las sustancias que producen solución conductora de electricidad cuando se disuelven en agua (o en otro disolvente polar) se denominan electrolitos.
Todos los compuestos iónicos, ácidos y bases producen iones en el agua y se clasifican como electrolitos.
Las sustancias que producen una solución eléctricamente no conductora cuando se disuelven en agua se denominan no electrolitos.
Los compuestos moleculares distintos de los ácidos y bases, como el metanol, la acetona, el azúcar y la glucosa, permanecen moléculas neutras cuando se disuelven en agua. Los solutos moleculares, distintos de ácidos y bases, no son electrolitos.
Electrolitos fuertes y débiles
Las sustancias que casi el 100% se disocian en iones cuando se disuelven en agua son electrolitos fuertes.
- Todos los compuestos iónicos que son solubles en agua son electrolitos fuertes.
- Los ácidos fuertes son electrolitos fuertes.
- Las bases fuertes son compuestos iónicos y electrolitos fuertes.
Un electrolito fuerte no significa que necesariamente sea altamente soluble en agua. Significa que la porción del soluto que se disuelve, también se disocia al 100% en iones en agua, por ejemplo, todos los compuestos iónicos. La solubilidad Ca (OH) 2 es solo 0.16 g Ca (OH) 2 /100 g agua a 20 o C, pero todos los Ca (OH) 2 disueltos se disocian en iones Ca 2 + y OH -.
Las bases fuertes son hidróxidos de metales alcalinos, es decir, LiOH, NaOH, KOH, RbOH y CsOH, e hidróxidos de metales alcalinotérreos pesados, es decir, Ca (OH) 2, Sr (OH) 2 y Ba (OH) 2, que son electrolitos fuertes. Los ácidos fuertes, es decir, HCl, HBr, HI, HClO 4, HNO 3 y H 2 SO 4, son compuestos moleculares pero son electrolitos fuertes porque se disocian casi 100% en iones cuando se disuelven en agua. Por ejemplo, el HCl se disocia casi por completo en iones cuando se disuelve en agua.
\ begin {ecuación}
\ mathrm {HCl} (\ mathrm {g}) +\ mathrm {H} _ {2}\ mathrm {O} (\ mathrm {l})\ rightarrow\ mathrm {H} _ {3}\ mathrm {O} ^ {1+} (\ mathrm {aq}) +\ mathrm {Cl} ^ {1-} (\ mathrm {aq})\ nonumber
\ fin {ecuación}
Las sustancias que se disocian parcialmente en iones cuando se disuelven en agua son electrolitos débiles. Los ácidos débiles y las bases débiles son electrolitos débiles.
Los ácidos semanales y las bases semanales, como el ácido acético (CH 3 COOH) y el amoníaco (NH 3), son solubles en agua, pero se disocian parcialmente en iones. Por ejemplo, si se disuelve 1 mol de ácido acético o 1 mol de amoníaco en 1 litro de agua a temperatura ambiente, establecen el siguiente equilibrio entre moléculas disueltas e iones disociados:
\ begin {ecuación}
\ begin {alineada}
&\ mathrm {CH} _ _ {3}\ mathrm {COOH} (\ mathrm {l})\ stackrel {\ text {Agua}} {\ longrightarrow}\ mathrm {CH} _ _ {3}\ mathrm {COOH} (\ mathrm {aq}) +\ mathrm {H} _ {2}\ mathrm {O} (\ mathrm {l})\ stackrel {\ rightarrow} {\ longleftarrow}\ mathrm {CH} _ {3}\ mathrm {COO} ^ {1-} (\ mathrm {aq}) +\ mathrm {H} _ {3}\ mathrm {O} ^ {1+} (\ mathrm {aq}),\\
&\ mathrm {NH} _ {3} (\ mathrm {~g})\ quad\ stackrel {\ texto {Agua}} {\ longrightarrow}\ mathrm {NH} _ {3} (\ mathrm {aq}) +\ mathrm {H} _ {2}\ mathrm {O} (\ mathrm {l})\ quad\ stackrel {\ rightarrow} {\ longleftarrow}\ mathrm {NH} _ {4} {} ^ {1+} (\ mathrm {aq}) +\ mathrm {OH} ^ {1-} (\ mathrm {aq}),
\ end {alineado}\ nonumber
\ end {ecuación}
donde solo aproximadamente 0.4% de las moléculas disueltas se disocian en iones, el restante aproximadamente 99.6% de las moléculas permanecen neutras. Los ácidos débiles y las bases débiles son electrolitos débiles.
La Fig. 5.3.2 ilustra la diferencia entre no electrolitos, electrolitos fuertes y electrolitos débiles.
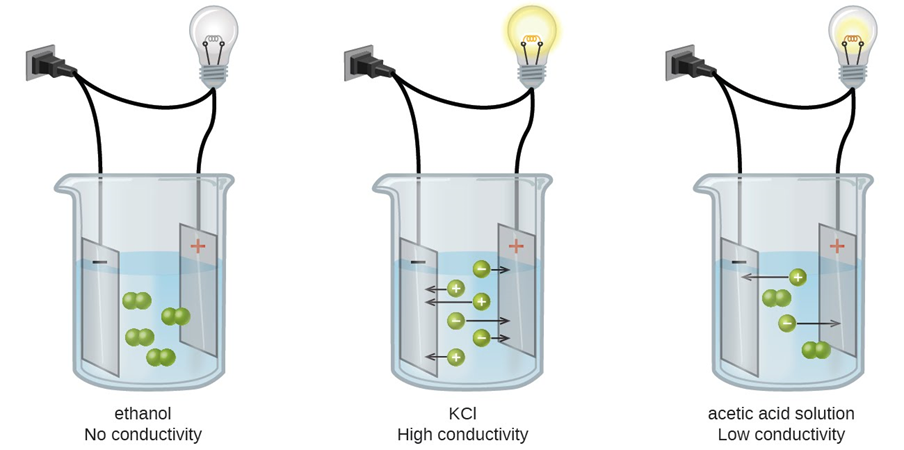
Figura\PageIndex{2}: Ilustración de un no electrolito que no conduce electricidad, un electrolito fuerte que tiene alta conductividad eléctrica y un electrolito débil que tiene baja conductividad eléctrica. Fuente: Karishma50/ (https; //creativecommons.org/licencias/by-sa/4.0)
Equivalente
La cantidad de moléculas y átomos se suele medir en moles. Los compuestos iónicos están compuestos por iones pero son neutros en general porque la carga +ve se equilibra con la carga —ve. Por lo tanto, la relación molar de cationes a aniones no siempre es de uno a uno. Por ejemplo, NaCl tiene una relación molar uno a uno de Na + y Cl -, pero CaCl 2 tiene una relación uno a dos de Ca 2 + y Cl -. Se introduce una nueva unidad, llamada equivalente (abreviada oficialmente como Equiv pero comúnmente abreviada como Eq), para diferenciar entre un mol de ion y un mol de carga en el ion.
El equivalente es la cantidad de una sustancia necesaria para reaccionar o suministrar un mol de iones hidrógeno (H +) en una reacción ácido-base, o reaccionar con o suministrar un mol de electrones en una reacción redox. En otras palabras, el número de equivalentes de un ion dado en una solución es igual al número de moles de ese ion multiplicado por su valencia.
1 \mathrm{~mol} \mathrm{~Na}^{+}=1 \mathrm{~Eq} \mathrm{~Na}^{+} \text {, but } \quad 1 \mathrm{~mol} \mathrm{~Ca}^{2+}=2 \mathrm{~Eq} \mathrm{~Ca}^{2+} \text {, and } 1 \mathrm{~mol} \mathrm{} \mathrm{~Al}^{3+}=3 \mathrm{~Ea} \mathrm{~Al}^{3+}\nonumber
Del mismo modo,
1 \mathrm{~mol} \mathrm{~Cl}^{-}=1 \mathrm{~Eq} \mathrm{~Cl}^{-}\text{, but} \quad 1 \mathrm{~mol} \mathrm{~CO}_{3}{ }^{2-}=2 \mathrm{~Eq} \mathrm{~CO}{ }_{3}{ }^{2-}\text{ and } 1 \mathrm{~mol} \mathrm{~PO}_{4}{ }^{3-}=3 \mathrm{~Ea} \mathrm{~PO}_{4}{ }^{3-}\nonumber
Las soluciones de electrolitos son globalmente neutras eléctricamente, es decir, el número de equivalentes de cationes es igual al número de equivalentes de aniones en la solución.
Por ejemplo, si se disuelve 1 mol de NaCl en agua, hay 1 Eq de iones Na + y 1 Eq de iones Cl - en la solución. Si se disuelve un mol de CaCl 2 en el agua hay 2 Eq de iones Ca 2 + y 2 Eq de iones Cl - en la solución. De igual manera, si se disuelven 1 mol de NaCl y 1 mol de AlCl 3 en el agua hay 1 Eq de iones Na +, 3 Eq de iones Al 3 +, y 4 Eq de iones Cl - para equilibrar los cationes en el agua.
La igualdad da dos factores de conversión. Por ejemplo, la igualdad 1 mol Ca 2 + = 2 Eq Ca 2 + da los siguientes dos factores de conversión:
\frac{1 \operatorname{~mol~} C a^{2+}}{2 ~E q ~C a^{2+}}\nonumber
y
\frac{2 ~E a ~C a^{2+}}{1 ~m o l ~C a^{2+}}\nonumber
El primer factor de conversión convierte la cantidad dada en equivalentes a moles, y el segundo convierte la cantidad dada en moles en equivalentes del ion como se explica en los siguientes ejemplos.
a) Calcular MeQ de Fe 3 + en 0.0200 mol de Fe 3 +? b) si el ión cloruro es el único anión en la solución, ¿cuántos MeQ de Cl - están presentes en la solución?
Solución
a) Dado 0.0200 mol Fe 3 +. MeQ Fe deseada 3 +.
La igualdad: 1 mol Fe 3 + = 3 Eq Fe 3 + da el factor de conversión\frac{3 ~E q ~F e^{3+}}{1 ~m o l ~F e^{3+}} que convierte la cantidad dada en moles a Eq de Fe 3 +. Otra igualdad: 1 Eq Fe 3 + = 1000 MeQ Fe 3 + da el factor de conversión\frac{1000 ~m E q ~F e^{3+}}{1 ~E q ~F e^{3+}}, que convierte la Eq de Fe 3 + en MeQ de Fe 3 +.
Cálculos:0.0200 \cancel{\text { mol } ~F e^{3+}} \times \frac{3 \cancel{~E q ~F e^{3+}}}{1 \cancel{~m o l ~F e^{3+}}} \times \frac{1000 ~m E q ~F e^{3+}}{1 \cancel{~E q ~F e^{3+}}}=60 ~mE q ~F e^{3+}\nonumber
Una solución salina interviniente contiene 145 mEq/L de Na +. ¿Cuántos moles de Na + hay en 0.500 L de la solución?
Solución
a) Dado: 145 mEq Na + /L de solución y 0.500 L de solución, Deseada:? mol Na +
Factores de conversión necesarios: La concentración en mEq/L es el primer factor para la conversión de L a mEq, la igualdad 1 mEq Na + = 1 mmol Na + da la segunda conversión necesaria para la conversión de MeQ a mmol, y la igualdad 1000 mmol Na + = 1 mol Na + dada la tercera factor de conversión necesario para la conversión de mEq a mol. Los tres factores de conversión se aplican uno tras otro en una sola fila en el siguiente cálculo:
0.500 \cancel{\text { L solution }} \times \frac{145 \cancel{\mathrm{~mEq} \mathrm{~Na}}}{1 \cancel{\text {L solution }}} \times \frac{1 \cancel{\mathrm{~mmol} \mathrm{~Na}^{+}}}{1 \cancel{\mathrm{~mEq} \mathrm{~Na}^{+}}} \times \frac{1 \mathrm{~mol} \mathrm{~Na}^{+}}{1000 \cancel{\mathrm{~mmol} \mathrm{~Na}^{+}}}=0.0725 \mathrm{~mol} \mathrm{~Na}^{+}\nonumber
Observe cómo las unidades del numerador en una fracción son canceladas por las unidades del denumerador de la siguiente fracción dejando solo las unidades deseadas sin cancelar que se convierten en las unidades del número de respuesta.
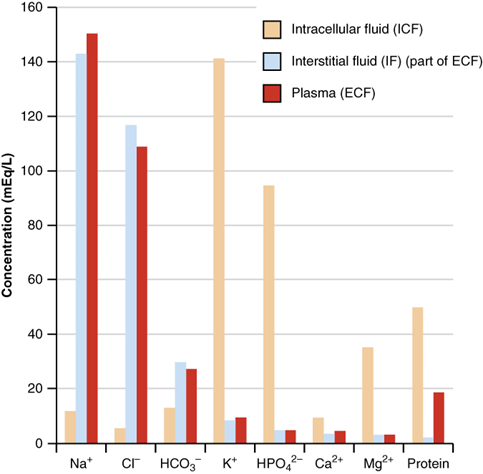
Electrolitos en fluidos corporales
La Fig. 5.3.3 muestra los electrolitos y sus concentraciones que se encuentran comúnmente en los fluidos corporales. Desempeñan un papel esencial en las funciones celulares y corporales. Por ejemplo, los iones de sodio regulan el contenido de agua y juegan un papel en la transmisión de impulsos eléctricos en el sistema nervioso. Los iones de potasio juegan un papel en el mantenimiento de un latido cardíaco regular y también juegan un papel en la transmisión de impulsos eléctricos. Los iones cloruro están ahí para equilibrar la carga. Los iones carbonato están involucrados en el mantenimiento del pH de la sangre.
Las concentraciones de electrolitos en los fluidos corporales no son lo suficientemente altas como para ser reportadas en un mol o unidades equivalentes. Los electrolitos en los fluidos corporales generalmente se reportan en unidades milimoles (mmol) o miliequivalentes (mEQ), donde:1000 \mathrm{~mmol}=1 \mathrm{~mol} y1000 \mathrm{~mEq}=1 \mathrm{~Eq}.
La concentración global de electrolitos en los fluidos intravenosos que se administran a los pacientes es aproximadamente la misma que la de los electrolitos en los fluidos corporales. Por ejemplo, la solución de lactato de Ringer contiene aproximadamente: 130 mEq/L Na +, 4 mEq/L K +, 3 mEq/L Ca 2 +, 109 mEq/L Cl - y 28 mEq/L lactato -. Tenga en cuenta que la carga total +ve (130+4+3= 137 meq/L) es igual a la carga general —ve (109+28 = 137 meq/L).