5.4: Concentración de soluciones

La concentración de una solución indica la cantidad de soluto disuelto en una cantidad dada de solución.

Hacer una solución de concentración de conocimiento

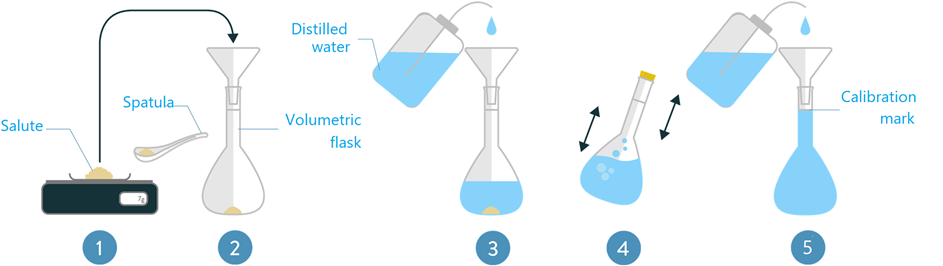
Una cantidad medida de soluto se disuelve en suficiente disolvente para hacer el volumen deseado de la solución, como se ilustra en la Fig. 5.4.1. La concentración de la solución se puede expresar de diferentes maneras usando unidades de masa, volumen o moles, como se explica a continuación.

Figura\(\PageIndex{1}\): Elaboración de una solución acuosa: 1) medir la masa del soluto en una balanza analítica, 2) verter el soluto en un matraz aforado de volumen conocido, 3) agregar agua destilada (o disolvente) a más de la mitad llenar el matraz, 4) tapar el matraz y agitarlo para disolver el soluto, 5) agregar más agua para llenar el matraz hasta la marca de calibración —medir desde el punto más bajo del menisco de agua, 6) tapar el matraz y agitar nuevamente para hacer una solución homogénea. Fuente: modificado de https://www.hiclipart.com/free-trans...cvcrq/download

Concentración en porcentaje (%)

Qué es por ciento (%)

El porcentaje (%) es un número o razón que representa una fracción de 100.

Por ejemplo, 5% significa 5:100, donde 5 es la parte, y 100 es el total. El porcentaje se calcula como cien veces de parte por total, es decir,

\ begin {ecuación}
\ texto {Porcentaje} (\%) =\ frac {\ texto {parte}} {\ texto {Total}}\ veces 100. \ nonumber
\ end {ecuación}

Ejemplo\(\PageIndex{1}\)

Se disuelve un NaCl de 50.0 g en agua para hacer una solución de 500 g. ¿Cuál es el porcentaje de NaCl en la solución?

Solución

Parte dada = 50.0 g NaCl, y total = 500 g de solución. Deseado: ¿% NaCl en la solución?

Fórmula:\(\text { Percentage }(\%)=\frac{\text { part }}{\text { Total }} \times 100 \text {. }\nonumber\)

Cálculos:\(\text { Percentage }(\%)=\frac{50.0 cancel{\mathrm{~g}}}{500 cancel{\mathrm{~g}}} \times 100=10.0 ~\% \mathrm{NaCl}\)

Las unidades cancelan en la parte de cálculo de fracciones, y se agrega un signo de% a la respuesta para decir que es una fracción de cien.

Porcentaje de masa (m/m)% de concentración

La concentración porcentual en masa expresa las unidades de masa de soluto en cien unidades de masa de la solución.

\ begin {ecuación}
\ nombreoperador {Masa} (\%) =\ frac {\ text {masa de soluto} (g)} {\ text {masa de soluto} (g) +\ text {masa de solvente} (g)}\ times 100=\ frac {\ text {masa de soluto} (g)} {\ text {masa de solución} (g)}\ veces 100\ nonumber
\ end {ecuación}

Obsérvese que el total es soluto y disolvente añadidos juntos, es decir, solución.

Ejemplo\(\PageIndex{2}\)

¿Cuál es el% en masa de NaOH en una solución preparada disolviendo 10.0 g NaOH en 100 g de agua?

Solución

Dado soluto = 10.0 g, y disolvente = 100 g, Deseado: Masa% NaOH?

Fórmula:\(\text { Mass }(\%)=\frac{\text { mass of solute }(g)}{\text { mass of solute }(g)+\text { mass of solvent }(g)} \times 100\)

Cálculos:\(\text { Mass }(\%)=\frac{10.0 \mathrm{~g} \mathrm{NaOH}}{(10.0 \mathrm{~g}+100 \mathrm{~g}) \text { solution }} \times 100=9.09 \% \mathrm{NaOH}\)

Tenga en cuenta que la concentración de% en masa y su recíproco son dos factores de conversión:\(\frac{\text { given } g \text { solute }}{100 g \text { solution }}\) y\(\frac{100 g \text { solution }}{\text { given g solute }}\)

Ejemplo\(\PageIndex{3}\)

El antibiótico de neosporina es una solución de neomicina al 3.5% m/m. ¿Cuántos gramos de neomicina hay en 50 g de ungüento?

Solución

Dado:\(3.5 \% \text { neomycin }=\frac{3.5 \mathrm{~g} \text { neomycin }}{100 \mathrm{~g} \text { solution }}\), y Cantidad de solución = 50 g, Deseado:? g neomicina

Cálculos:\[50 \cancel{\mathrm{~g} \text { solution }} \times \frac{3.5 \mathrm{~g} \text { neomycin }}{100 \cancel{\mathrm{~g} \text { solution }}}=1.8 \mathrm{~g} \text { neomycin. }\nonumber\]

Porcentaje en volumen (v/v)% de concentración

La concentración porcentual en volumen expresa las unidades de volumen de soluto en cien unidades de volumen de la solución.

La forma matemática del% v/v es:

\ begin {ecuación}
\ text {Volumen} (\%) =\ frac {\ text {volumen de soluto} (\ mathrm {mL})} {\ text {volumen de solución} (\ mathrm {mL})}\ times 100\ nonumber
\ end {ecuación}

La Fig. 5.4.2 muestra los intervalos de concentración porcentual en volumen de diferentes clases de fragancias.

Figura\(\PageIndex{2}\): Esta infografía explica las diferencias entre Parfums, Perfumes, Eau de Perfume, Eau de Parfum, Eau de Toilette y Colonia. También da una idea aproximada de cómo varía la concentración de aceites Parfum a medida que avanzamos hacia aromas más ligeros. Fuente: Nicole Smith/CC BY-SA (https://creativecommons.org/licenses/by-sa/4.0)

Ejemplo\(\PageIndex{4}\)

¿Cuál es el% en volumen de extracto de rosa en una solución preparada disolviendo 14.0 mL de extracto de rosa en un solvente para hacer 200 mL de solución?

Solución

Dado: Soluto = 14.0 g, y solución = 200 g, Deseado: Volumen% solución de rosa?

Fórmula:\ begin {ecuación}
\ text {Volumen} (\%) =\ frac {\ text {volumen de soluto} (m L)} {\ text {volumen de solución} (m L)}\ times 100\ nonumber
\ end {ecuación}

Cálculos:\ begin {ecuación}
\ text {Volumen} (\%) =\ frac {14\ mathrm {~mL}\ text {extracto de rosa}} {200\ mathrm {~mL}\ text {solution}}\ times 100=7.0\%\ text {solución rosa}\ nonumber
\ end {ecuación}

Los dos factores de conversión para v/v% concentración son:\ begin {ecuación}
\ frac {\ text {dado mL soluto}} {100\ mathrm {~mL}\ text {solution}}\ quad\ text {, y}\ quad\ frac {100\ mathrm {~mL}\ text {solution}} {\ text {dado}\ mathrm {~mL}\ text {soluto}\ nonumbte er
\ end {ecuación}

Ejemplo\(\PageIndex{5}\)

¿Cuál es el volumen de bromo (Br ₂) en 250 mL de 4.8% v/v de solución de Br ₂ en tetracloruro de carbono?

Solución

Dado: Concentración 4.8% v/v bromo\(=\frac{4.8 ~m L \text { bromine }}{100 ~m L \text { solution }}\), volumen de solución = 250 mL, Deseado: Volumen de soluto, es decir,? mL de bromo.

Cálculos:\ [
250\ mathrm {~mL}\ text {solution}\ times\ frac {4.8\ mathrm {~mL}\ text {bromo}} {100\ mathrm {~mL}\ text {solution}.} =12\ mathrm {~mL ~bromo}\ text {.}\ nonumber\]

Porcentaje masa/volumen (m/v)% de concentración

La concentración porcentual masa/volumen expresa las unidades de masa de soluto en cien unidades de volumen de solución.

La forma matemática de m/v% es:

\ begin {ecuación}
\ text {masa/volumen} (\%) =\ frac {\ text {masa de soluto} (g)} {\ text {volumen de solución} (m L)}\ times 100\ nonumber
\ end {ecuación}

Ejemplo\(\PageIndex{6}\)

¿Cuál es el% masa/volumen de solución de glucosa que se prepara disolviendo 50 g de glucosa en agua suficiente para hacer 1000 mL de solución?

Solución

Dado: Soluto = 50.0 g, y Solución = 1000 mL, Deseado: Masa/volumen% solución de glucosa?

Fórmula:\ begin {ecuación}
\ text {masa/volumen} (\%) =\ frac {\ text {masa de soluto} (g)} {\ text {volumen de solución} (m L)}\ times 100\ nonumber
\ end {ecuación}

Cálculos:\ begin {ecuación}
\ frac {\ text {Mass}} {\ text {volume}} (\%) =\ frac {50\ mathrm {~g}\ text {glucosa}} {1000\ mathrm {~mL}\ text {solution}}\ times 100=5.0\%\ text {solución de glucosa por}\ frac {\ mathrm {m}} {\ mathrm {v}}. \ nonumber
\ end {ecuación}

Los dos factores de conversión de ms/v% concentración son:\ begin {equation}
\ frac {\ text {dado} g\ text {soluto}} {100\ mathrm {~mL}\ text {solution}}\ quad\ text {y}\ quad\ frac {100\ mathrm {~mL}\ text {solution}} {\ text {dado}\ mathrm {g}\ text {soluto}}\ nonumber
\ end { ecuación}

Ejemplo\(\PageIndex{7}\)

¿Cuántos gramos de antibióticos de clindamicina hay en una cápsula de 45 mL de la clindamicina al 1.0% (m/v)?

Solución

Dado:% m/v concentración: 1.08% m/v clindamicina\(=\frac{1.0 \mathrm{~g} \text { clindamycin }}{100 \mathrm{~mL} \text { solution }}\), y volumen de solución = 45 mL, Deseado:? g clindamicina?

Cálculos:\ begin {ecuación}
45\ text {mL solution}\ times\ frac {1.0\ mathrm {~g}\ text {clindamicina}} {100\ mathrm {~mL}\ text {solution}} =4.5\ mathrm {~g}\ text {clindamicina.}\ nonumber
\ end {ecuación}

Concentración de partes por millón (ppm) y partes por mil millones (ppb)

Partes por millón (ppm) es un número o proporción expresado como una fracción de millón (10 ⁶).

Por ejemplo, 2 ppm significa\(\frac{2}{1,000,000}\) o 2:1 ,000,000, donde 2 es la parte, y 1,000,000 es el total. La concentración en ppm se calcula como un millón de veces de parte por total, es decir:\ begin {ecuación}
\ text {Concentración en ppm} =\ frac {p a r t} {\ text {Total}}\ times 10^ {6}\ nonumber
\ end {ecuación}

Partes por mil millones (ppb) es un número o proporción expresado como una fracción de mil millones (10 ⁹).

Es decir:\ begin {ecuación}
\ text {Concentración en ppb} =\ frac {\ text {part}} {\ text {Total}}\ times 10^ {9}\ nonumber
\ end {ecuación}

Al igual que la concentración porcentual, los ppm y ppb pueden ser masa/masa (m/m), volumen/volumen (v/v) o masa/volumen (m/v).

Ejemplo\(\PageIndex{8}\)

El límite de acción de la EPA para el cobre es de 1.3 mg/L en agua potable. ¿Cuál es este límite en ppm de cobre m/v en el agua potable?

Solución

Dado: 1.3 mg de cobre en solución de 1L, Deseado:? ppm m/v de Cobre en agua

Fórmula:\(\text { Concentration in ppm }=\frac{\operatorname{solute}(\mathrm{~g})}{\operatorname{solution}(\mathrm{~mL})} \times 10^{6}\)

Cálculos: Primero, convierta las unidades dadas de masa y volumen en las unidades correspondientes que tome la fórmula, luego conecte los valores en la fórmula y calcule.

\[\text { Solute }=1.3 \mathrm{~mg} \times \frac{1 \mathrm{~g}}{1000 \mathrm{~mg}}=0.0013 \mathrm{~g}\nonumber\]

\[\text { Solution }=1 \mathrm{~L} \times \frac{1000 \mathrm{~mL}}{1 \mathrm{~L}}=1000 \mathrm{~mL}\nonumber\]

\[\text { Concentration in ppm }=\frac{0.0013 \mathrm{~g}}{1000 \mathrm{~mL}} \times 10^{6}=1.3 \mathrm{~ppm} \text { copper } v / \mathrm{m}\nonumber\]

Ejemplo\(\PageIndex{9}\)

El límite de acción de la EPA para el plomo es de 0.015 mg/L en agua potable. ¿Cuál es este límite en ppb de plomo m/v en el agua potable?

Solución

Dado: 0.015 mg en solución de 1L, Deseado:? ppb m/v de Plomo en agua

Fórmula:\(\text { Concentration in ppb }=\frac{\operatorname{solute}(g)}{\operatorname{solution}(\mathrm{mL})} \times 10^{9}\)

Cálculos: Primero, convierta las unidades dadas de masa y volumen en las unidades correspondientes que tome la fórmula, luego conecte los valores en la fórmula y calcule.

\[\text { Solute }=0.015 \mathrm{~mg} \times \frac{1 \mathrm{~g}}{1000 \mathrm{~mg}}=0.000015 \mathrm{~g}\nonumber\]

\[\text { Solution }=1 \mathrm{~L} \times \frac{1000 \mathrm{~mL}}{1 \mathrm{~L}}=1000 \mathrm{~mL}\nonumber\]

\[\text { Concentration in ppb }=\frac{0.000015 \mathrm{~g}}{1000 \mathrm{~mL}} \times 10^{9}=15 \mathrm{~ppb} \text { lead } \mathrm{v} / \mathrm{m}\nonumber\]

Molaridad

La molaridad (M) expresa los moles de soluto en un litro de solución.

La unidad de concentración de solución más común utilizada en química es la molaridad (M):

\[\operatorname{Molarity}~({M})=\frac{n~(\text {moles of solute })}{V ~\text { (Litters of solution })}\nonumber\]

Ejemplo\(\PageIndex{10}\)

¿Cuál es la molaridad (M) de una solución preparada disolviendo 50.0 g de NaOH en suficiente agua para hacer 250 mL de solución?

Solución

Dado: Soluto = 50.0 g NaOH, Volumen de solución = 250 mL, Deseado:? ¿Solución M de NaOH?

Fórmula:\(\text { Molarity }(M)=\frac{n~(\text {moles of solute })}{V~(\text {Litters of solution })}\)

Cálculos: Primero, convierta las unidades dadas de masa y volumen en las unidades correspondientes que tome la fórmula, luego conecte los valores en la fórmula y calcule.

\[\text { Solute }=50.0 \mathrm{~g} \mathrm{~NaOH} \times \frac{1 \mathrm{~mol} \mathrm{~NaOH}}{40.00 \mathrm{~g} \mathrm{~NaOH}}=1.25 \mathrm{~mol} \mathrm{~NaOH}\nonumber\]

\[\text { Solution }=250 \mathrm{~mL} \times \frac{1 \mathrm{~L}}{1000 \mathrm{~mL}}=0.250 \mathrm{~L}\nonumber\]

\[\text { Molarity }(M)=\frac{1.25 \mathrm{~mol} \mathrm{~NaOH}}{0.250 \mathrm{~L} \mathrm{~solution}}=5.00 \mathrm{~M} \mathrm{~NaOH}\nonumber\]

Los dos factores de conversión de molaridad son los siguientes:

\[\frac{n \text { (moles of solute) }}{V \text { (Litters of solution) }} \quad\text { and }\quad \frac{V \text { (Litters of solution) }}{n \text { (moles of solute })}\nonumber\]

Ejemplo\(\PageIndex{11}\)

¿Cuántas camadas de solución de HCl 0.211 M se necesitan para proporcionar 0.400 mol de HCl?

Solución

Dado: cantidad de soluto = 0.400 mol HCl, Concentración de soluto = 0.211M =\(\frac{0.211 \text { mol HCl}}{1 L \text { solution }}\)

Cálculos:\[\text { Liters of solution needed }=0.400 \mathrm{~mol} \mathrm{~HCl} \times \frac{1 \mathrm{~L} \text { soluton }}{0.211 \mathrm{~mol} \mathrm{~HCl}}=1.90 \mathrm{~L} \text { solution }\nonumber\]

Ejemplo\(\PageIndex{12}\)

Una solución de 2.50 L de NaOH 1.12 M contiene ¿cuántos moles de NaOH?

Solución

Dado: Volumen de solución = 2.50 L de solución, concentración de solución =\(1.12 \mathrm{~M} \mathrm{~NaOH}=\frac{1.12 \mathrm{~mol} \mathrm{~NaOH}}{1 \mathrm{~L} \text { solution }}\), Deseado:? ¿moles de NaOH?

Cálculos:\[\text { Moles of } \mathrm{~NaOH} \text { in the solution }=2.50 \text { L solution } \times \frac{1.12 \mathrm{~mol} \mathrm{~NaOH}}{1 \mathrm{~L} \text { solution }}=2.80 \mathrm{~mol} \mathrm{} \mathrm{~NaOH}\nonumber\]

Dilución de soluciones

La dilución de una solución es la adición de un disolvente para disminuir la concentración de soluto del soluto en la solución.

El producto de concentración (C) y volumen (V) es la cantidad de soluto, es decir,

\ begin {ecuación}
\ text {Cantidad de soluto} =C\ text {in}\ frac {\ text {cantidad de soluto}} {\ text {volumen de solución}}\ veces V\ text {en volumen de solución.}\ nonumber
\ end {ecuación}

La cantidad de soluto no cambia añadiendo disolvente. Por lo tanto, el producto de concentración y volumen, es decir, CV, que es la cantidad de soluto, es una constante, es decir,

\ begin {ecuación}
C_ {1} V_ {1} =C_ {2} V_ {2} =\ texto {cantidad de soluto}\ nonumber
\ end {ecuación}

Figura\(\PageIndex{3}\): Esta imagen ilustra que cuando se mezcla más disolvente con la solución, la cantidad de soluto permanece igual, pero su concentración disminuye. Fuente: Theislikerice/CC BY-SA (https://creativecommons.org/licenses/by-sa/4.0)

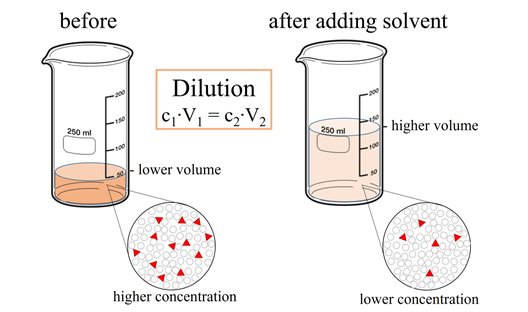
_{La Fig. 5.4.3 muestra que si la concentración inicial es C1, el volumen inicial es V 1, y después de la dilución, la concentración final es C 2, el volumen final es V 2, luego C 1 V 1 = C 2 V 2 = cantidad de} soluto que es constante. Si se conocen tres de las cuatro variables en esta ecuación, se puede calcular la que falta, como se explica en el siguiente ejemplo.

Precaución

Tenga en cuenta que las concentraciones y volúmenes deben estar en las mismas unidades en ambos lados de la ecuación: C ₁ V ₁ = C ₂ V ₂. Si no están en las mismas unidades, conviértalas a las mismas unidades antes de sumergirlas en la fórmula.

Ejemplo\(\PageIndex{13}\)

¿Cuánto volumen de HCl 11.3 M se necesita para preparar 250 mL de HCl 2.00 M?

Solución

Dado: C ₁ = 11.3 M HCl, C ₂ = 2.00 M HCl, V ₂ = 250 mL solución, Deseado V ₁ =?

Fórmula: C ₁ V ₁ = C ₂ V ₂, reordenarlo para aislar el parámetro deseado:\(V_{1}=\frac{C_{2} V_{2}}{C_{1}}\)

Cálculos:\[V_{1}=\frac{C_{2} V_{2}}{C_{1}}=\frac{2.00 \mathrm{~M~HCl} \times 250 \mathrm{~mL} \text { solution }}{11.3 \mathrm{~M} \mathrm{~HCl}}=44.2 \mathrm{~mL} \text { solution }\nonumber\]

Ejemplo\(\PageIndex{14}\)

¿Cuál es la molaridad de la solución de NaOH preparada diluyendo 100 mL de solución de NaOH 0.521 M a 500 mL?

Solución

Dado C ₁ = 0.521 M NaOH, V ₁ = 100 mL solución, V ₂ = 500 mL solución, Deseado: Concentración de la solución final C ₂ =? NaOH M

Fórmula: C ₁ V ₁ = C ₂ V ₂, reorganizar para aislar el parámetro deseado:\(C_{2}=\frac{C_{1} V_{1}}{V_{2}}\)

Cálculos:\[C_{2}=\frac{C_{1} V_{1}}{V_{2}} = \frac{0.521 \mathrm{~M~NaOH} \times 100 \mathrm{~mL} \mathrm{~NaOH}}{500 \mathrm{~mL} \mathrm{~NaOH}}=0.104 \mathrm{~M~NaOH}\nonumber\]

Ejemplo\(\PageIndex{15}\)

La dopamina se administra por vía intravenosa a un paciente para aumentar la presión arterial. ¿Cuántos mililitros (mL) de una solución de dopamina al 4.0% (m/v) se necesitan para preparar 250 mL de una solución al 0.030% m/v)?

Solución

Dado: C ₁ = 4.0% (m/v), C ₂ = 0.030% (m/v), V ₂ = 250 mL solución, Deseado V ₁ =?

Fórmula: C ₁ V ₁ = C ₂ V ₂, reorganizar para aislar el parámetro deseado:\(V_{1}=\frac{C_{2} V_{2}}{C_{1}}\)

Cálculos:\[V_{1}=\frac{C_{2} V_{2}}{C_{1}}=\frac{0.030 \% \times 250 \mathrm{~mL} \text { solution }}{4.0 \%}=5.0 \mathrm{~mL} \text { of solution }\nonumber\]

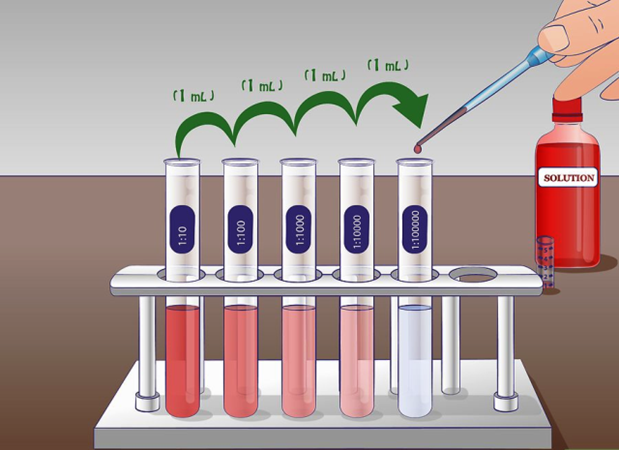
dilución logarítmica

Tomar un volumen unitario de una solución dada y agregar suficiente disolvente para aumentar el volumen de la solución 10 veces para un diluitón logarítmico.

Una dilución logarítmica es diez veces la dilución, es decir, probada por la siguiente fórmula:\[C_{2}=\frac{C_{1} V_{1}}{V_{2}}=\frac{1 \mathrm{~mL} \times C_{1}}{10 \mathrm{~mL}}=0.1 \times C_{1}\nonumber\]

Repetir el paso anterior con la solución diluida da como resultado 10x10 = dilución de 100 veces, y repetir la tercera vez resulta en 10x10x10 = dilución de 1000 veces. Esta dilución de 10 veces en cada paso se denomina dilución logarítmica. La Fig. 5.4.4 muestra que cinco etapas de dilución logarítmica en una solución inicial al 10% dan como resultado una concentración de 10 ppm en la solución final.

Figura\(\PageIndex{4}\): Dilución logarítmica: cinco etapas de dilución logarítmica sobre una solución inicial al 10% dan como resultado una concentración de 10 ppm de la solución final. Fuente: Grasso Luigi/CC BY-SA (https://creativecommons.org/licenses/by-sa/4.0)