6.6: Las leyes simples del gas
- Page ID
- 72352
- Conoce lo que se entiende por el término leyes de gas.
- Conoce las diferentes unidades de presión.
- Aprender y aplicar la ley de Boyle.
- Aprender y aplicar la ley de Carlos.
- Aprender y aplicar la ley de Gay-Lussac.
El comportamiento de los gases se puede modelar con leyes de gas. La ley de Boyle relaciona la presión y el volumen de un gas a temperatura y cantidad constantes. La ley de Charles relaciona el volumen y la temperatura de un gas a presión y cantidad constantes. En las leyes de gas, las temperaturas siempre deben expresarse en Kelvin.
Un barómetro mide la presión del gas por la altura de la columna de mercurio. Una unidad de presión de gas es el milímetro de mercurio\(\left( \text{mm} \: \ce{Hg} \right)\). Una unidad equivalente a la\(\text{mm} \: \ce{Hg}\) se llama la\(\text{torr}\), en honor al inventor del barómetro, Evangelista Torricelli. El pascal\(\left( \text{Pa} \right)\) es la unidad estándar de presión. Un pascal es una cantidad muy pequeña de presión, por lo que la unidad más útil para las presiones diarias de gas es el kilopascal\(\left( \text{kPa} \right)\). Un kilopascal equivale a 1000 pascales. Otra unidad de presión comúnmente utilizada es la atmósfera\(\left( \text{atm} \right)\). La presión atmosférica estándar se llama\(1 \: \text{atm}\) de presión y es igual a\(760 \: \text{mm} \: \ce{Hg}\) y\(101.3 \: \text{kPa}\). La presión atmosférica también se indica a menudo como libras por pulgada cuadrada\(\left( \text{psi} \right)\). La presión atmosférica al nivel del mar es\(14.7 \: \text{psi}\).
\[1 \: \text{atm} = 760 \: \text{mm} \: \ce{Hg} = 760 \: \text{torr} = 101.3 \: \text{kPa} = 14.7 \: \text{psi} \nonumber \]
Ley de Boyle: Presión y Volumen
Cuando los científicos del siglo XVII comenzaron a estudiar las propiedades físicas de los gases, notaron algunas relaciones simples entre algunas de las propiedades medibles del gas. Toma presión (P) y volumen (V), por ejemplo. Los científicos señalaron que para una cantidad dada de un gas (generalmente expresado en unidades de moles [n]), si la temperatura (T) del gas se mantenía constante, la presión y el volumen estaban relacionados: A medida que uno aumenta, el otro disminuye. A medida que uno disminuye, el otro aumenta. Decimos que la presión y el volumen están inversamente relacionados.
Sin embargo, hay más: la presión y el volumen de una cantidad dada de gas a temperatura constante están relacionados numéricamente. Si toma el valor de presión y lo multiplica por el valor de volumen, el producto es una constante para una cantidad dada de gas a una temperatura constante:
\[P × V = \text{ constant at constant n and T} \nonumber \]
Si el volumen o la presión cambian mientras la cantidad y la temperatura permanecen iguales, entonces la otra propiedad debe cambiar para que el producto de las dos propiedades siga igual a esa misma constante. Es decir, si las condiciones originales están etiquetadas\(P_1\) y\(V_1\) y las nuevas condiciones están etiquetadas\(P_2\) y\(V_2\), tenemos
\[P_1V_1 = \text{constant} = P_2V_2 \nonumber \]
donde se supone que las propiedades se multiplican juntas. Dejando fuera la parte media, simplemente tenemos
\[P_1V_1 = P_2V_2 \text{ at constant n and T} \nonumber \]
Esta ecuación es un ejemplo de una ley de gas. Una ley de gas es una fórmula matemática simple que permite modelar, o predecir, el comportamiento de un gas. Esta particular ley del gas ia llamó a la ley de Boyle, después del científico inglés Robert Boyle, quien la anunció por primera vez en 1662. La figura\(\PageIndex{1}\) muestra dos representaciones de cómo funciona la ley de Boyle.
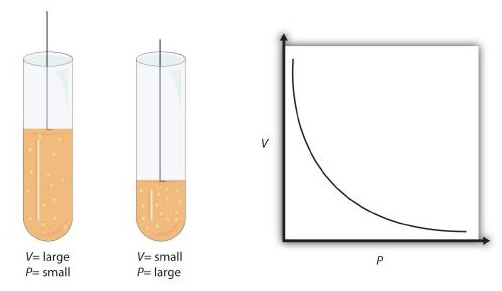
La ley de Boyle es un ejemplo de un segundo tipo de problema matemático que vemos en la química, uno basado en una fórmula matemática. Las tácticas para trabajar con fórmulas matemáticas son diferentes de las tácticas para trabajar con factores de conversión. Primero, la mayoría de las preguntas que tendrás que responder usando fórmulas son preguntas tipo palabra, por lo que el primer paso es identificar qué cantidades se conocen y asignarlas a variables. Segundo, en la mayoría de las fórmulas, se deben realizar algunos reordenamientos matemáticos (es decir, álgebra) para resolver una variable desconocida. La regla es que para encontrar el valor de la variable desconocida, se debe aislar matemáticamente la variable desconocida por sí misma y en el numerador de un lado de la ecuación. Por último, las unidades deben ser consistentes. Por ejemplo, en la ley de Boyle hay dos variables de presión; deben tener la misma unidad. También hay dos variables de volumen; también deben tener la misma unidad. En la mayoría de los casos, no importará cuál sea la unidad, pero la unidad debe ser la misma en ambos lados de la ecuación.
Una muestra de gas tiene una presión inicial de 2.44 atm y un volumen inicial de 4.01 L. Su presión cambia a 1.93 atm. ¿Cuál es el nuevo volumen si la temperatura y la cantidad se mantienen constantes?
Solución
Pasos para la resolución de problemas |
Ejemplo\(\PageIndex{1}\) |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | \ (\ pageIndex {1}\)” style="vertical-align:middle; ">
Dado: P 1 = 2.44 atm y V 1 = 4.01 L P 2 = 1.93 atm Encuentra: V 2 =? L |
| Enumere otras cantidades conocidas. | \ (\ PageIndex {1}\)” style="vertical-align:middle; ">none |
| Planear el problema. | \ (\ pageIndex {1}\)” style="vertical-align:middle; ">
Primero, reorganizar la ecuación algebraicamente para resolver para\(V_2\). \[V_2 = \frac{P_1 \times V_1}{P_2} \nonumber \] |
| Cancelar unidades y calcular. | \ (\ pageIndex {1}\)” style="vertical-align:middle; ">
Ahora sustituya las cantidades conocidas en la ecuación y resuelva. \[V_2 = \frac{2.44 \: \cancel{\text{atm}} \times 4.01 \: \text{L}}{1.93 \: \cancel{atm}} = 5.07 \: \text{L} \nonumber \] |
| Piensa en tu resultado. | \ (\ PageIndex {1}\)” style="vertical-align:middle; ">Sabemos que la presión y el volumen están inversamente relacionados; a medida que uno disminuye, el otro aumenta. La presión está disminuyendo (de 2.44 atm a 1.93 atm), por lo que el volumen debe estar aumentando para compensar, y es (de 4.01 L a 5.07 L). Entonces la respuesta tiene sentido basada en la ley de Boyle. |
Si P 1 = 334 torr, V 1 = 37.8 mL, y P 2 = 102 torr, ¿qué es V 2?
- Contestar
-
124 mL
Como se mencionó, puede usar cualquier unidad para presión o volumen, pero ambas presiones deben expresarse en las mismas unidades, y ambos volúmenes deben expresarse en las mismas unidades.
Una muestra de gas tiene una presión inicial de 722 torr y un volumen inicial de 88.8 mL. Su volumen cambia a 0.663 L. ¿Cuál es la nueva presión?
Solución
Pasos para la resolución de problemas |
Ejemplo\(\PageIndex{2}\) |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | \ (\ PageIndex {2}\)” style="vertical-align:middle; ">
Dado: P 1 = 722 torr y V 1 = 88.8 mL V 2 = 0.633 L Encuentra: P 2 =? torr |
| Enumere otras cantidades conocidas. | \ (\ PageIndex {2}\)” style="vertical-align:middle; ">1 L = 1000 mL para tener las mismas unidades para volumen. |
| Planear el problema. | \ (\ PageIndex {2}\)” style="vertical-align:middle; ">
1. Realizar la conversión de la segunda unidad de volumen de L a mL. 2. Reorganizar la ecuación algebraicamente para resolver para\(P_2\). \[P_2 = \frac{P_1 \times V_1}{V_2} \nonumber \] |
| Cancelar unidades y calcular. | \ (\ PageIndex {2}\)” style="vertical-align:middle; ">
1. \[0.663\, \cancel{L}\times \frac{1000\, ml}{1\, \cancel{L}}=663\, ml \nonumber \] 2. Sustituir las cantidades conocidas en la ecuación y resolver. \[P_2 = \frac{722 \: \text{torr} \times 88.8 \: \cancel{\text{mL}}}{663 \: \cancel{\text{mL}}} = 96.7 \: \text{torr} \nonumber \] |
| Piensa en tu resultado. | \ (\ PageIndex {2}\)” style="vertical-align:middle; ">Cuando el volumen aumentó, la presión disminuyó, que es como se esperaba para la ley de Boyle. |
Si V 1 = 456 mL, P 1 = 308 torr y P 2 = 1.55 atm, ¿qué es V 2?
- Contestar
-
119 mL
Ley de Carlos: Temperatura y Volumen
El físico francés Jacques Charles (1746 - 1823) estudió el efecto de la temperatura sobre el volumen de un gas a presión constante. La Ley de Carlos establece que el volumen de una masa dada de gas varía directamente con la temperatura absoluta del gas cuando la presión se mantiene constante. La temperatura absoluta es la temperatura medida con la escala Kelvin. Se debe usar la escala Kelvin porque cero en la escala Kelvin corresponde a una detención completa del movimiento molecular.
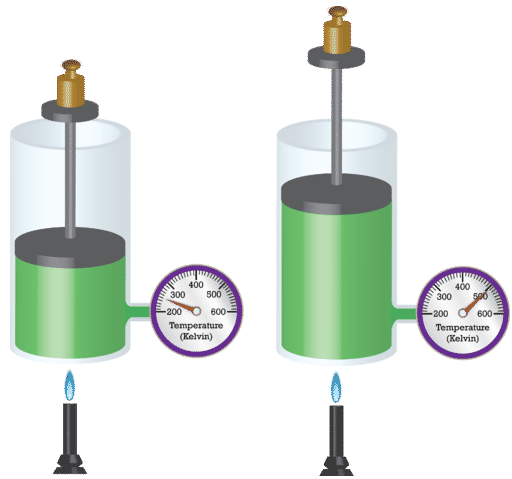
Matemáticamente, la relación directa de la Ley de Carlos puede ser representada por la siguiente ecuación:
\[\frac{V}{T} = k \nonumber \]
Al igual que con la Ley de Boyle,\(k\) es constante sólo para una muestra de gas dada. La siguiente tabla muestra los datos de temperatura y volumen para una cantidad establecida de gas a presión constante. La tercera columna es la constante para este conjunto de datos en particular y siempre es igual al volumen dividido por la temperatura Kelvin.
| Temperatura\(\left( \text{K} \right)\) | Volumen\(\left( \text{mL} \right)\) | \(\frac{V}{T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) |
|---|---|---|
| \ (\ left (\ text {K}\ right)\)” style="vertical-align:middle; text-align:center; ">50 | \ (\ left (\ text {mL}\ right)\)” style="vertical-align:middle; text-align:center; ">20 | \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="vertical-align:middle; text-align:center;" >0.40 |
| \ (\ left (\ text {K}\ right)\)” style="vertical-align:middle; text-align:center; ">100 | \ (\ left (\ text {mL}\ right)\)” style="vertical-align:middle; text-align:center; ">40 | \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="vertical-align:middle; text-align:center;" >0.40 |
| \ (\ left (\ text {K}\ right)\)” style="vertical-align:middle; text-align:center; ">150 | \ (\ left (\ text {mL}\ right)\)” style="vertical-align:middle; text-align:center; ">60 | \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="vertical-align:middle; text-align:center;" >0.40 |
| \ (\ left (\ text {K}\ right)\)” style="vertical-align:middle; text-align:center; ">200 | \ (\ left (\ text {mL}\ right)\)” style="vertical-align:middle; text-align:center; ">80 | \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="vertical-align:middle; text-align:center;" >0.40 |
| \ (\ left (\ text {K}\ right)\)” style="vertical-align:middle; text-align:center; ">300 | \ (\ left (\ text {mL}\ right)\)” style="vertical-align:middle; text-align:center; ">120 | \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="vertical-align:middle; text-align:center;" >0.40 |
| \ (\ left (\ text {K}\ right)\)” style="vertical-align:middle; text-align:center; ">500 | \ (\ left (\ text {mL}\ right)\)” style="vertical-align:middle; text-align:center; ">200 | \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="vertical-align:middle; text-align:center;" >0.40 |
| \ (\ left (\ text {K}\ right)\)” style="vertical-align:middle; text-align:center; ">1000 | \ (\ left (\ text {mL}\ right)\)” style="vertical-align:middle; text-align:center; ">400 | \ (\ frac {V} {T} = k\)\(\left( \frac{\text{mL}}{\text{K}} \right)\) "style="vertical-align:middle; text-align:center;" >0.40 |
Cuando se grafica estos datos, el resultado es una línea recta, indicativa de una relación directa, que se muestra en la siguiente figura.
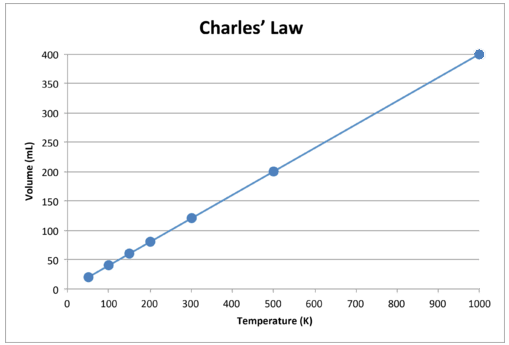
Observe que la línea va exactamente hacia el origen, es decir, que a medida que la temperatura absoluta del gas se acerca a cero, su volumen se acerca a cero. Sin embargo, cuando un gas se lleva a temperaturas extremadamente frías, sus moléculas eventualmente se condensarían en estado líquido antes de alcanzar el cero absoluto. La temperatura a la que se produce este cambio al estado líquido varía para los diferentes gases.
La Ley de Carlos también se puede utilizar para comparar las condiciones cambiantes de un gas. Ahora usamos\(V_1\) y\(T_1\) para reposar el volumen inicial y la temperatura de un gas, mientras\(V_2\) y\(T_2\) representamos el volumen y la temperatura finales. La relación matemática de la Ley de Carlos se convierte en:
\[\frac{V_1}{T_1} = \frac{V_2}{T_2} \nonumber \]
Esta ecuación se puede utilizar para calcular cualquiera de las cuatro cantidades si se conocen las otras tres. La relación directa sólo se mantendrá si las temperaturas se expresan en Kelvin. Las temperaturas en Celsius no funcionarán. Recordemos la relación que\(\text{K} = \: ^\text{o} \text{C} + 273\).
Un globo se llena a un volumen de\(2.20 \: \text{L}\) a una temperatura de\(22^\text{o} \text{C}\). Luego se calienta el balón a una temperatura de\(71^\text{o} \text{C}\). Encuentra el nuevo volumen del globo.
Solución
Pasos para la resolución de problemas |
Ejemplo\(\PageIndex{3}\) |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | \ (\ PageIndex {3}\) ">
Dado: \(V_1 = 2.20 \: \text{L}\)y \(T_1 = 22^\text{o} \text{C} = 295 \: \text{K}\) \(T_2 = 71^\text{o} \text{C} = 344 \: \text{K}\) Encuentra: V 2 =? L |
| Enumere otras cantidades conocidas. | \ (\ PageIndex {3}\) ">Las temperaturas se han convertido primero a Kelvin. |
| Planear el problema. | \ (\ PageIndex {3}\) ">
Primero, reorganizar la ecuación algebraicamente para resolver para\(V_2\). \[V_2 = \frac{V_1 \times T_2}{T_1} \nonumber \] |
| Cancelar unidades y calcular. | \ (\ PageIndex {3}\) ">
Ahora sustituya las cantidades conocidas en la ecuación y resuelva. \[V_2 = \frac{2.20 \: \text{L} \times 344 \: \cancel{\text{K}}}{295 \: \cancel{\text{K}}} = 2.57 \: \text{L} \nonumber \] |
| Piensa en tu resultado. | \ (\ PageIndex {3}\) ">El volumen aumenta a medida que aumenta la temperatura. El resultado tiene tres cifras significativas. |
Si V 1 = 3.77 L y T 1 = 255 K, ¿qué es V 2 si T 2 = 123 K?
- Contestar
-
1.82 L
Una muestra de un gas tiene un volumen inicial de 34.8 L y una temperatura inicial de −67°C. ¿Cuál debe ser la temperatura del gas para que su volumen sea 25.0 L?
Solución
Pasos para la resolución de problemas |
Ejemplo\(\PageIndex{4}\) |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | \ (\ PageIndex {4}\) “>
Dado: Dado: T 1 = -27 o C y V 1 = 34.8 L V 2 = 25.0 L Encuentra: T 2 =? K |
| Enumere otras cantidades conocidas. | \ (\ PageIndex {4}\) “>K = -27 o C + 273 |
| Planear el problema. | \ (\ PageIndex {4}\) “>
1. Convertir la temperatura inicial a Kelvin 2. Reorganizar la ecuación algebraicamente para resolver para\(T_2\). \[T_2 = \frac{V_2 \times T_1}{V_1} \nonumber \] |
| Cancelar unidades y calcular. | \ (\ PageIndex {4}\) “>
1. −67 °C + 273 = 206 K 2. Sustituir las cantidades conocidas en la ecuación y resolver. \[T_2 = \frac{25.0 \: \cancel{\text{L}} \times 206 \: \text{K}}{34.8 \: \cancel{\text{L}}} = 148 \: \text{K} \nonumber \] |
| Piensa en tu resultado. | \ (\ PageIndex {4}\) “>Esto también es igual a −125°C. A medida que disminuye la temperatura, el volumen disminuye, lo que hace en este ejemplo. |
Si V 1 = 623 mL, T 1 = 255°C, y V 2 = 277 mL, ¿qué es T 2?
- Contestar
-
235 K, o −38°
Ley de Gay-Lussac: Temperatura y Presión
Cuando se incrementa la temperatura de una muestra de gas en un recipiente rígido, también aumenta la presión del gas. El aumento de la energía cinética da como resultado que las moléculas de gas golpeen las paredes del contenedor con más fuerza, resultando en una mayor presión. El químico francés Joseph Gay-Lussac (1778 - 1850) descubrió la relación entre la presión de un gas y su temperatura absoluta. La Ley de Gay-Lussac establece que la presión de una determinada masa de gas varía directamente con la temperatura absoluta del gas, cuando el volumen se mantiene constante. La Ley de Gay-Lussac es muy similar a la Ley de Carlos, siendo la única diferencia el tipo de contenedor. Mientras que el contenedor en un experimento de la Ley de Carlos es flexible, es rígido en un experimento de Ley de Gay-Lussac.
Las expresiones matemáticas para la Ley de Gay-Lussac son igualmente similares a las de la Ley de Carlos:
\[\frac{P}{T} \: \: \: \text{and} \: \: \: \frac{P_1}{T_1} = \frac{P_2}{T_2} \nonumber \]
Un gráfico de presión vs. temperatura también ilustra una relación directa. A medida que un gas se enfría a volumen constante, su presión disminuye continuamente hasta que el gas se condensa en un líquido.
El gas en una lata de aerosol está bajo una presión de\(3.00 \: \text{atm}\) a una temperatura de\(25^\text{o} \text{C}\). Es peligroso desechar una lata de aerosol por incineración. ¿Cuál sería la presión en el aerosol a una temperatura de\(845^\text{o} \text{C}\)?
Solución
Pasos para la resolución de problemas |
Ejemplo\(\PageIndex{5}\) |
|---|---|
| Identifica la información “dada” y cuál es el problema que te pide “encontrar”. | \ (\ PageIndex {5}\) ">
Dado: \(P_1 = 3.00 \: \text{atm}\) \(T_1 = 25^\text{o} \text{C} = 298 \: \text{K}\) \(T_2 = 845^\text{o} \text{C} = 1118 \: \text{K}\) Encuentra: \(P_2 = ? \: \text{atm}\) |
| Enumerar otras cantidades conocidas | \ (\ PageIndex {5}\) ">Las temperaturas se han convertido primero a Kelvin. |
| Planear el problema | \ (\ PageIndex {5}\) ">
Primero, reorganizar la ecuación algebraicamente para resolver para\(P_2\). \[P_2 = \frac{P_1 \times T_2}{T_1} \nonumber \] |
| Calcular | \ (\ PageIndex {5}\) ">
Ahora sustituya las cantidades conocidas en la ecuación y resuelva. \[P_2 = \frac{3.00 \: \text{atm} \times 1118 \: \cancel{\text{K}}}{298 \: \cancel{\text{K}}}= 11.3 \: \text{atm} \nonumber \] |
| Piensa en tu resultado. | \ (\ PageIndex {5}\) ">La presión aumenta dramáticamente debido al gran aumento de la temperatura. |
Volumen molar
Ya debería ser obvio que algunas propiedades físicas de los gases dependen fuertemente de las condiciones. Lo que necesitamos es un conjunto de condiciones estándar para que las propiedades de los gases puedan compararse adecuadamente entre sí. Temperatura y Presión Estándar (STP) se define como exactamente 100 kPa de presión (0.986 atm) y 273 K (0°C). Para simplificar, utilizaremos 1 atm como presión estándar. Definir STP nos permite comparar más directamente las propiedades de los gases que difieren entre sí.
Una propiedad compartida entre los gases es el volumen molar. El volumen molar es el volumen de 1 mol de un gas. En STP, el volumen molar de un gas se puede determinar fácilmente usando la ley de gas ideal:
\[(1\, atm)V=(1\, mol)(0.08205\frac{L.atm}{mol.K})(273\, K) \nonumber \]
Todas las unidades cancelan excepto L, la unidad de volumen. Entonces V = 22.4 L
Obsérvese que no hemos especificado la identidad del gas; solo hemos especificado que la presión es de 1 atm y la temperatura es de 273 K. Esto hace que sea una aproximación muy útil: cualquier gas en STP tiene un volumen de 22.4 L por mol de gas; es decir, el volumen molar a STP es de 22.4 L/mol (Fig. 6.6.1 Molar Volumen). Este volumen molar hace un factor de conversión útil en problemas estequiométricos si las condiciones están en STP. Si las condiciones no están en STP, no es aplicable un volumen molar de 22.4 L/mol. Sin embargo, si las condiciones no están en STP, se puede usar la ley de gas combinado para calcular cuál sería el volumen del gas si se encuentra en STP; entonces se puede usar el volumen molar de 22.4 L/mol.
¿Cuántos moles de Ar están presentes en 38.7 L en STP?
Solución
Podemos usar el volumen molar, 22.4 L/mol, como factor de conversión, pero necesitamos revertir la fracción para que las unidades L cancelen y se introduzcan unidades mol. Se trata de una conversión de un solo paso:
\[38.7\, \not{L}\times \frac{1\, mol}{22.4\not{L}}=1.73\, mol \nonumber \]
¿Qué volumen tiene 4.87 mol de Kr en STP?
109 L
La química está en todas partes: la respiración
La respiración (más propiamente llamada respiración) es el proceso por el cual aspiramos aire a nuestros pulmones para que nuestros cuerpos puedan tomar oxígeno del aire. Apliquemos las leyes de gas a la respiración.
Comience por considerar la presión. Atraemos aire a nuestros pulmones porque el diafragma, un músculo debajo de los pulmones, se mueve hacia abajo para reducir la presión en los pulmones, haciendo que el aire externo se apresure para llenar el volumen de menor presión. Expultimos aire por el diafragma empujando contra los pulmones, aumentando la presión dentro de los pulmones y forzando el aire de alta presión a salir. ¿Cuáles son los cambios de presión involucrados? ¿Un cuarto de ambiente? ¿Una décima parte de un ambiente? En realidad, en condiciones normales, es solo 1 o 2 torr de diferencia de presión lo que nos hace inhalar y exhalar.
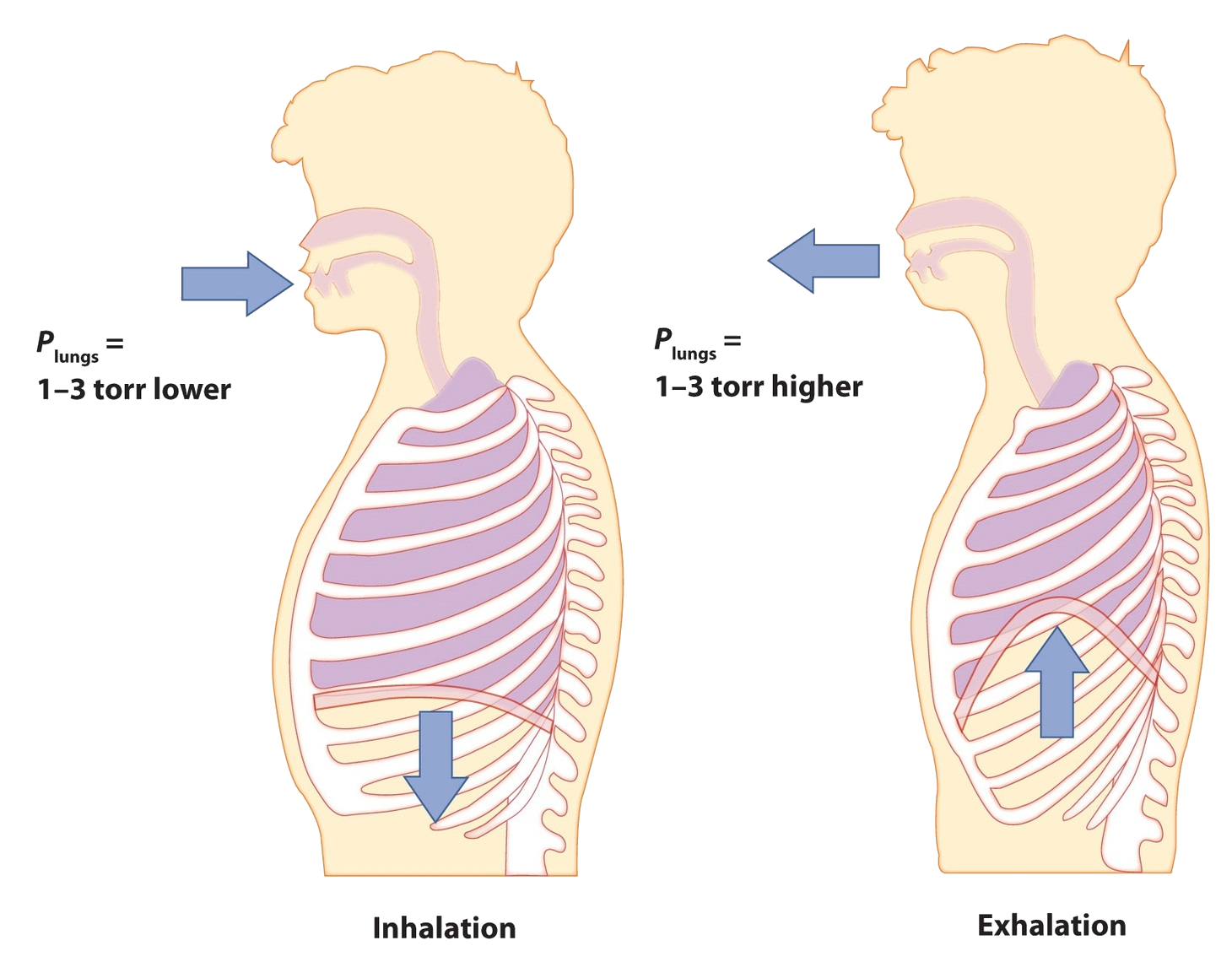
Una respiración normal es de aproximadamente 0.50 L. Si la temperatura ambiente es de aproximadamente 22°C, entonces el aire tiene una temperatura de aproximadamente 295 K. Con una presión normal de 1.0 atm, ¿cuántos moles de aire absorbimos por cada respiración? La ley de gas ideal nos da una respuesta:
\[(1.0\, atm)(0.50\, L)=n(0.08205\frac{L.atm}{mol.K})(295\, K) \nonumber \]
Resolviendo por el número de lunares, obtenemos
n = 0.021 mol de aireEsto termina siendo alrededor de 0.6 g de aire por respiración—no mucho sino suficiente para mantenernos vivos.
Resumen
- El comportamiento de los gases se puede modelar con leyes de gas.
- La ley de Boyle relaciona la presión y el volumen de un gas a temperatura y cantidad constantes.
- La ley de Charles relaciona el volumen y la temperatura de un gas a presión y cantidad constantes.
- La Ley de Gay-Lussac establece que la presión de una determinada masa de gas varía directamente con la temperatura absoluta del gas, cuando el volumen se mantiene constante.
- En las leyes de gas, las temperaturas siempre deben expresarse en Kelvin.
Colaboradores y Atribuciones
CK-12 Foundation by Sharon Bewick, Richard Parsons, Therese Forsythe, Shonna Robinson, and Jean Dupon.
Henry Agnew (UC Davis)