4.3: Reología

Las mediciones de viscosidad son el reino de un campo de la ciencia llamado reología. La reología es, literalmente, el estudio del flujo. Otra definición muy sencilla, atribuida al ingeniero químico Chris Macosko de la Universidad de Minnesota, es el estudio de “qué pasa cuando aplasta cosas”. Aquí también entra en juego un elemento de fuerza o presión.

Una de las formas comunes de evaluar propiedades en reología es colocar una muestra entre dos placas paralelas y mover una placa con respecto a la otra. Un plato dice quieto y el otro se mueve. ¿Qué pasa con el líquido entre las placas? Debe haber cierta fricción entre la placa estacionaria y el líquido que mantendrá el líquido quieto. También debería haber cierta fricción entre la placa móvil y el líquido que hará que el líquido se mueva a la misma velocidad que esa placa. Entonces en un extremo, el líquido se mueve junto con la placa deslizante y en el otro extremo el líquido está perfectamente quieto. Si imaginamos que el líquido entre estos dos extremos se divide en capas muy delgadas, entonces cada capa debe estar moviéndose a una velocidad ligeramente diferente a la siguiente.

En el diagrama, el símbolo, u, representa la velocidad de la capa de líquido. La flecha al lado de la capa está destinada a transmitir su velocidad relativa: la capa superior se mueve más rápido, la siguiente capa es un poco más lenta, y así sucesivamente; la capa inferior no se mueve en absoluto. Existe una cantidad importante, llamada tasa de deformación o velocidad de cizallamiento (dada como símbolo la letra griega gamma, γ, con un punto en la parte superior) que describe cómo cambia la velocidad del líquido que se mueve a lo largo del eje x (izquierda a derecha), capa por capa, en la dirección y.

¿Qué tiene que ver esta imagen con la viscosidad? Bueno, para que esa placa superior se mueva, tenemos que aplicarle algún tipo de fuerza. En reología la fuerza se da por unidad de área (como presión); esta fuerza por unidad de área se describe como la tensión (dada como símbolo la letra griega sigma, σ).

¿Y si quisiéramos deslizar la placa aún más rápido? ¿Qué pasaría con el líquido? Bueno, la velocidad de cizallamiento subiría. La capa superior se estaría moviendo aún más rápido, y la capa inferior aún estaría estacionaria. ¿Y qué tendríamos que hacer para conseguir esa velocidad de cizallamiento más rápida? Tendríamos que empujar un poco más fuerte la placa superior. El resultado es una gráfica que se ve así:

El gráfico dice que el esfuerzo cortante y la velocidad de cizallamiento están directamente relacionados. El esfuerzo se llama “esfuerzo cortante” debido a la dirección de la fuerza paralela al líquido, causando deformación por cizallamiento. Cuando aumentamos la velocidad de cizallamiento, el esfuerzo cortante también aumenta proporcionalmente. Entonces, si hiciéramos este experimento usando agua como líquido entre las placas, obtendríamos una relación lineal entre el esfuerzo cortante y la velocidad de cizallamiento. Así describió Sir Isaac Newton el comportamiento de los líquidos, así que cuando vemos esa relación lineal entre tensión y deformación, describimos al líquido como un líquido newtoniano.

¿Qué pasa si hacemos el experimento con miel en lugar de agua? ¿Qué pasaría, por ejemplo, si ejerciéramos cierta tensión para obtener cierta velocidad de cizallamiento con el agua, y quisiéramos obtener la misma tasa de cizallamiento usando miel? Bueno, la miel es más espesa que el agua. No se va a mover tan fácilmente. Tendremos que aplicar un mayor esfuerzo para lograr la misma velocidad de cizallamiento que medimos con agua.

Eso sería cierto para cada velocidad de cizallamiento posible. Si tuviéramos que graficar el esfuerzo cortante vs. esfuerzo cortante con miel, obtendríamos una relación lineal, tal como lo hicimos con el agua, pero el valor del esfuerzo cortante siempre sería mayor que para el agua. La pendiente de la línea para la miel sería mayor que la pendiente de la línea para el agua.

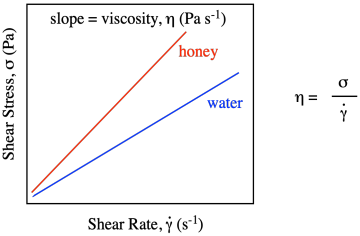
La viscosidad se define formalmente como la pendiente de esa línea. La miel, al ser más espesa que el agua, requiere tensiones cada vez mayores para lograr las mismas tasas de deformación que obtendrías usando tensiones más bajas con agua. En el sencillo análogo de cocina del experimento, tienes que empujar la cuchara más fuerte para revolver la miel de lo que haces si solo estás revolviendo agua.

La miel y el agua son líquidos newtonianos. La relación es simple: aumentar el esfuerzo cortante y aumentar la velocidad de cizallamiento. No todos los líquidos se comportan de esa manera. Las soluciones poliméricas no lo hacen, por ejemplo. Presentan una relación no lineal, en la que las tensiones de cizallamiento necesarias para obtener velocidades de cizallamiento más altas no son tan altas como cabría esperar.

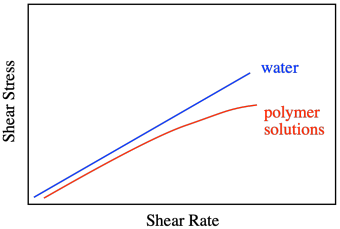
Ese comportamiento se describe como adelgazamiento por cizallamiento. ¿Qué hace que las soluciones poliméricas hagan eso? Recuerde que, en solución, una molécula de polímero individual tiende a arrollarse en una bola. Normalmente, esas bolas son esféricas. A altas velocidades de cizallamiento, se distorsionan en elipses. Eso reduce la cantidad de arrastre, haciendo que la solución sea un poco menos viscosa de lo que cabría esperar. El esfuerzo cortante aún aumenta con mayores velocidades de cizallamiento, pero no tanto como si se tratara de un fluido newtoniano.

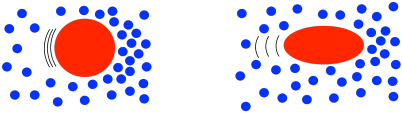
Eso no es todo. Recuerde, los polímeros muestran enredos de cadena, especialmente cuando son muy grandes. El enredo de la cadena aumenta la viscosidad de la solución. Estas cadenas son móviles porque el polímero está constantemente experimentando cambios conformacionales. A medida que la solución se esquilea, algunas de las cadenas de polímero pueden moverse sueltas de sus vecinos, pero los cambios conformacionales aleatorios siempre darán como resultado nuevos enredos de inmediato.

Pero, ¿qué sucede a una tasa muy alta de deformación por cizallamiento? Las cadenas de polímeros aún se desenredan, pero no tienen tiempo para formar nuevos enredos, porque todo está zumeando demasiado rápido. Sin esos enredos, la viscosidad no aumenta tan bruscamente como cabría esperar.

Algunos líquidos se comportan igual que el agua, pero las soluciones de polímeros no. Esa es una consecuencia de las estructuras de cadena enormemente larga de los polímeros. Vale la pena señalar que hay otras cosas que no se comportan de la manera “normal”. Los coloides suelen mostrar espesamiento por cizallamiento. Se pueden ver ejemplos de esto en videos de personas corriendo por pozas para vadear llenas de almidón de maíz y agua, una mezcla coloidal en la que las partículas sólidas de almidón de maíz simplemente se suspenden en el agua, no disueltas. Si cruzas la piscina, te hundes. Si corres, te quedas en la cima. Eso es espesamiento por cizallamiento, y tiene que ver con cómo esas partículas sólidas se mueven durante el cizallamiento. Cuando caminas, simplemente se deslizan uno junto al otro, pero cuando corres, todos chocan y se detienen.

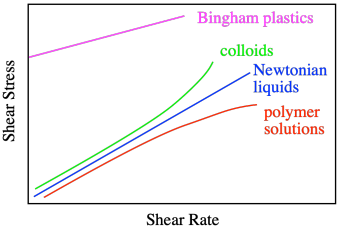
Un plástico Bingham, en cambio, en realidad parece ser un sólido hasta que le das un buen empujón; luego fluye como un líquido. La mantequilla de maní se comporta así.

Ejercicio 4.3.1

La miel es un fluido newtoniano, pero la melaza se somete a adelgazamiento por cizalladura. ¿Qué podrías deducir sobre la composición de la melaza y la miel?