IV. Explicando la filicidad radical

A. Teoría de los Vínculos de Valencia

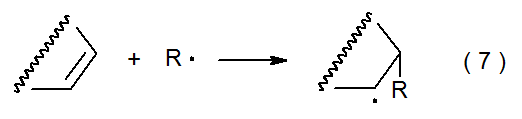
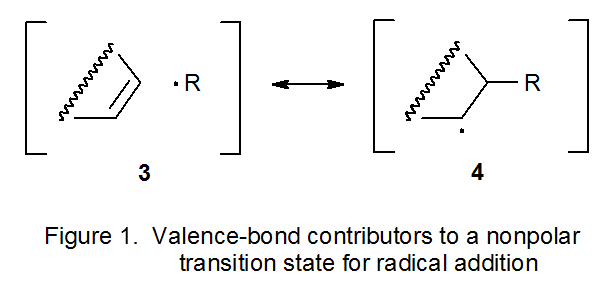
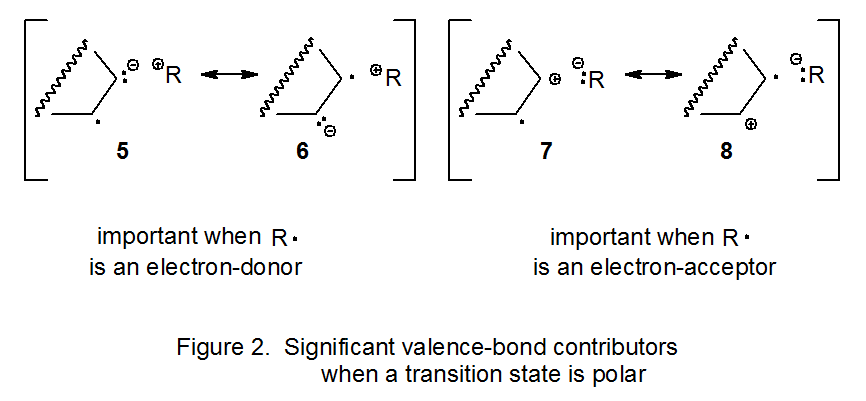
Una forma de explicar la existencia de filicidad radical comienza con la reacción de adición mostrada en la ecuación 7. La estructura de estado de transición en esta reacción se puede representar como un híbrido de estructuras de enlace de valencia. Si no hay separación de carga, el estado de transición puede ser representado por los contribuyentes 3 y 4 mostrados en la Figura 1. La distribución desigual de electrones en el estado de transición se puede tener en cuenta al incluir contribuyentes de resonancia adicionales. Si en el estado de transición hay una transferencia de densidad electrónica de R· al doble enlace C-C, esta transferencia se puede representar sumando los contribuyentes 5 y 6 (Figura 2). Si la transferencia de electrones está en la otra dirección, los contribuyentes de resonancia 7 y 8 (pero no 5 y 6) hacen una contribución significativa a la estructura del estado de transición (Figura 2).

1. Radicales Nucleofílicos

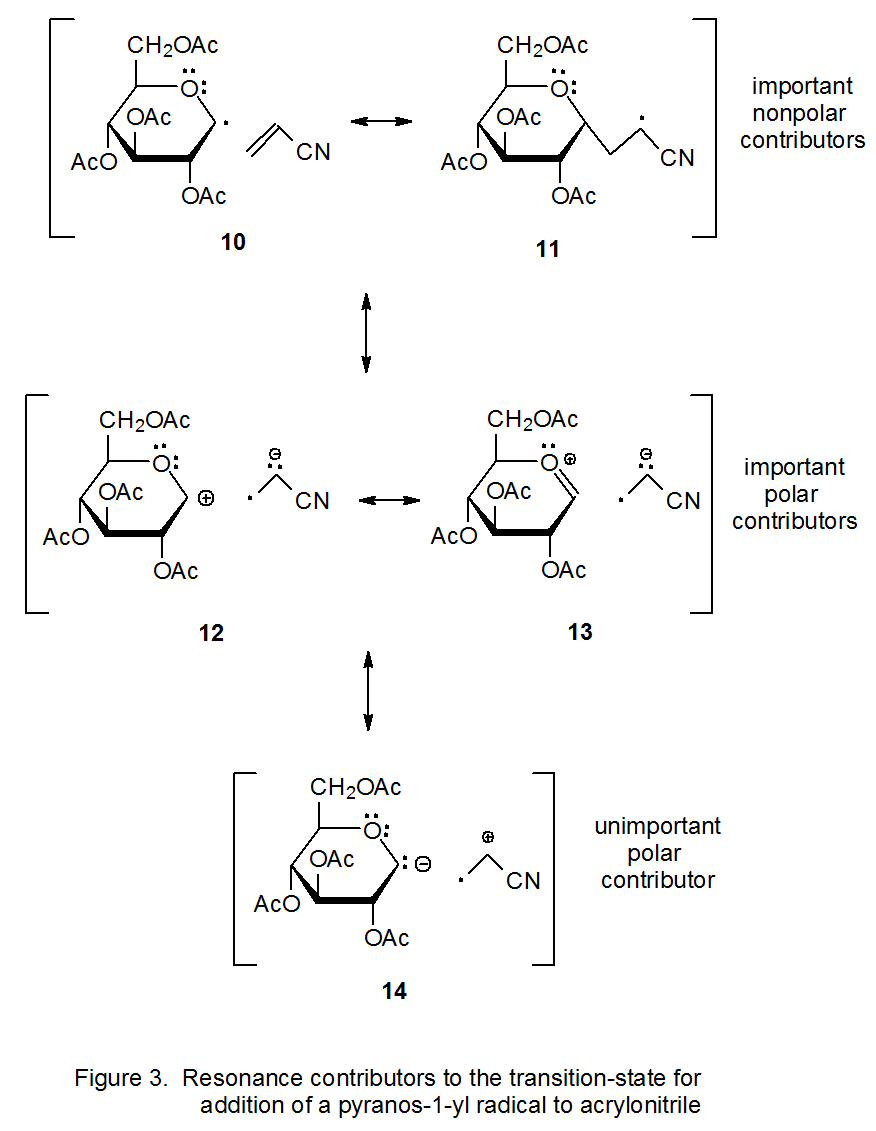
Para ilustrar la forma en que la teoría del enlace de valencia explica la nucleofilia radical, es instructivo examinar la reacción mostrada en la ecuación 8. En esta reacción el radical D-glucopiranos-1-ilo 9 se considera nucleófilo debido a que se suma al doble enlace deficiente en electrones en acrilonitrilo. ²⁴ Las estructuras de enlace de valencia 10 - 14 (Figura 3) contribuyen potencialmente a la estructura de estado de transición en esta reacción. Las estructuras 10 y 11 son contribuyentes importantes que no tienen separación de carga. Las estructuras 12 y 13 son contribuyentes menores pero significativos, menores porque implican separación de carga pero significativas porque estabilizan efectivamente las cargas negativas (12) o positivas y negativas (13). La estructura 14 no es significativa porque tiene separación de carga y las cargas no están efectivamente estabilizadas. Dado que las estructuras 12 y 13 hacen una mayor contribución que 14 al estado de transición en esta reacción (eq 8), el radical 9 se convierte en un donador de electrones neto en el estado de transición y, por lo tanto, se considera nucleófilo.

2. Radicales electrofílicos

Si un centro radical tiene un sustituyente (o sustituyentes) atrayentes de electrones suficientemente fuertemente unidos, el carácter inherentemente nucleófilo de un radical centrado en carbono se reduce hasta el punto de que el radical se vuelve electrófilo. ¹⁸ Por ejemplo, el radical malonilo 1, que tiene dos grupos aceptores de electrones unidos al centro radical, se considera electrofílico porque se suma al doble enlace rico en electrones en el D-glucal 2 (eq 3). ⁷ La electrofilicidad de 1 puede entenderse principalmente en términos de la importancia para la estructura de estado de transición del contribuyente de transferencia de carga 15, una estructura en la que los grupos metoxicarbonil aceptores de electrones estabilizan la carga negativa y la átomo de oxígeno del anillo estabiliza la carga positiva (Figura 4). Juntas, estas interacciones estabilizadoras aumentan la contribución en el estado de transición desde una estructura en la que el radical 1 está actuando como electrófilo al aceptar la densidad electrónica del D-glucal 2. La estructura de resonancia 16 no es un contribuyente importante en el estado de transición porque dentro de 16 hay un desplazamiento desestabilizador de la densidad electrónica lejos de un centro radical que contiene sustituyentes metoxicarbonil aceptores de electrones.

3. Radicales ambifílicos

Inherente a definir la filicidad radical en términos de transferencia de electrones es la idea de que la filicidad de un radical es una función de la reacción en cuestión. Esto significa que en lugar de describir a un radical como nucleofílico, debe describirse como nucleofílico en una reacción particular. Es justo decir, sin embargo, que los radicales que son moderadamente o fuertemente electrofílicos o nucleófilos en una reacción probablemente tengan la misma filicidad en todas las reacciones, pero los radicales que son débilmente nucleofílicos o electrófilos en una reacción son mejores candidatos para un cambio de filicidad en una reacción. Los radicales que son nucleofílicos en una reacción pero electrófilos en otra se clasifican como ambifílicos.

B. Teoría Orbital Molecular: Interacciones Fronteria-Orbital

Cuando una estructura de estado de transición para una reacción se asemeja a la estructura de los materiales de partida, las interacciones frontera-orbital proporcionan información cualitativa sobre los cambios energéticos que ocurren en el estado de transición. (Dado que los orbitales fronterizos se basan en las estructuras de los materiales de partida, cuanto más lejos esté el estado de transición a lo largo de la vía de reacción, las interacciones frontera-orbital menos confiables serán en la predicción o racionalización de la reactividad). Según el postulado de Hammond ²⁵, una reacción exotérmica debe tener un estado de transición temprana con una estructura parecida a la de los materiales de partida; por lo tanto, dicha reacción debería ser adecuada para su análisis por interacciones fronte-orbital. Una reacción que implica la adición de un radical centrado en carbono a un doble enlace carbono-carbono es un candidato principal para este tipo de análisis porque dicha reacción reemplaza un enlace π por un enlace σ más estable, un cambio que debería producir una reacción decididamente exotérmica. ^1,3,6,26

1. Radicales Nucleofílicos

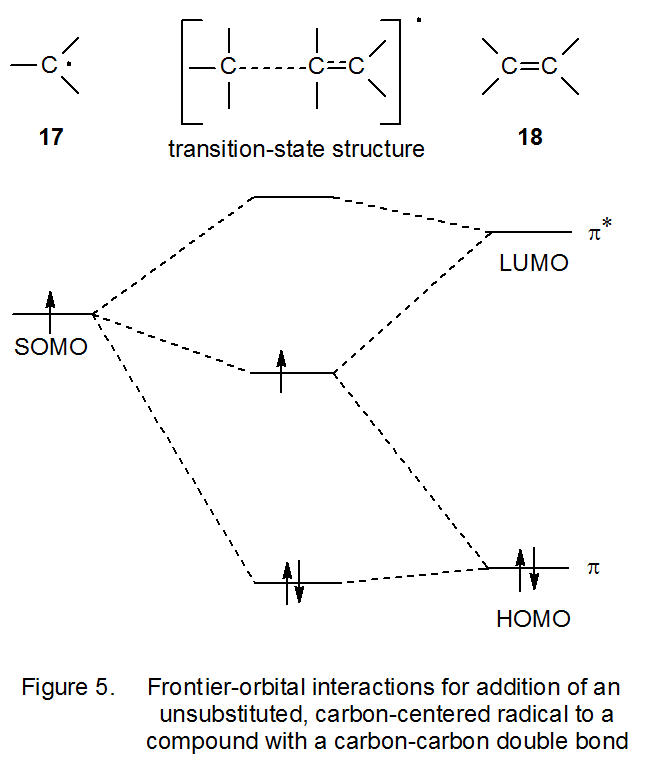
Un punto de partida para explicar la nucleofilia radical en términos de interacciones frontera-orbital se encuentra en la Figura 5, que muestra el orbital molecular ocupado individualmente (SOMO) en el radical 17 interactuando con los orbitales π* (LUMO) y π (HOMO) del alqueno 18. Identificar la interacción más importante es fundamental para determinar la nucleofilia del radical sumador. Cuando el SOMO de 17 interactúa con el alqueno 18, la mayor interacción es con el orbital π* del alqueno (Figura 5). ⁶ La evidencia convincente que respalda esta posición proviene de graficar las energías HOMO y LUMO calculadas de alquenos sustituidos contra el logaritmo natural de las constantes de velocidad relativa (ln k _rel) para la adición de un radical centrado en carbono (el radical terc- butilo fue usado) a estos alquenos. ²⁷ Existe una correlación lineal entre las energías ln k _rel y LUMO, pero no existe tal correlación entre las energías ln k _rel y HOMO. La correlación con las energías LUMO es entonces consistente con la interacción fronte-orbital dominante entre el SOMO del radical 17 y el orbital π* del alqueno 18 (Figura 5).

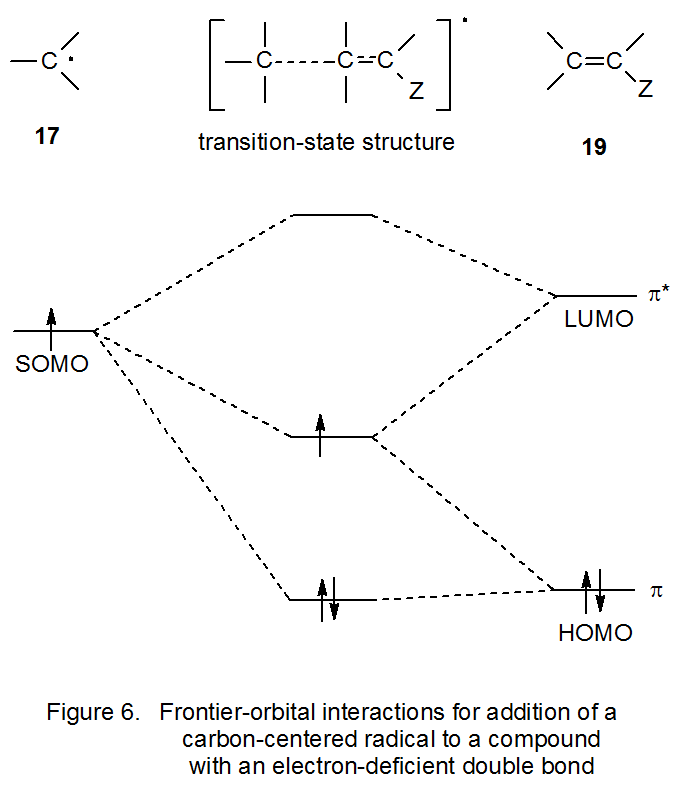
El siguiente paso para entender cómo las interacciones frontera-orbital pueden explicar la nucleofilia radical implica la adición del radical 17 al alqueno 19, un compuesto en el que el doble enlace contiene el sustituyente aceptor de electrones Z (Figura 6). Cuando Z reemplaza uno de los átomos de hidrógeno unidos a un átomo de carbono doblemente unido, el orbital π* se estabiliza y el nivel de energía asociado se acerca al del SOMO de 17. ²⁸ Este cambio en la posición del nivel de energía aumenta la interacción entre el SOMO y el orbital π* (Figura 6). Una mayor interacción se traduce en una barrera de estado de transición inferior para la reacción; por lo tanto, el radical 17 se agregará más rápidamente al alqueno que contiene el grupo Z aceptor de electrones que a un alqueno no sustituido. Esta reacción preferencial con alquenos deficientes en electrones hace que el radical 17 sea nucleófilo.

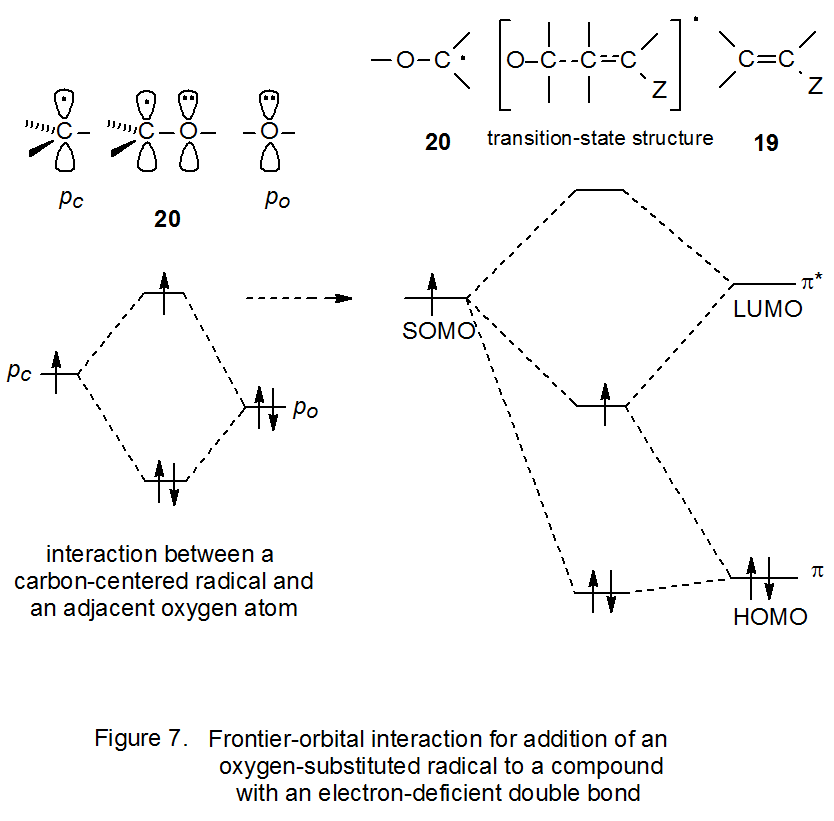
Es posible aumentar aún más la nucleofilia de un radical centrado en carbono si su nivel de energía SOMO se acerca aún más al del orbital π* de un alqueno. Este tipo de cambio ocurre cuando un átomo de oxígeno se une directamente al centro radical porque la interacción entre el orbital de tipo p en el átomo de carbono y el orbital de tipo p en el átomo de oxígeno adyacente eleva el nivel de energía SOMO en el radical resultante (20) ( Figura 7). Este nivel de energía superior coloca el SOMO más cerca energéticamente al orbital π* del alqueno reactivo. Tal cambio aumenta aún más la interacción orbital y al hacerlo provoca una mayor estabilización del estado de transición. La reactividad potenciada, debido a la presencia del átomo de oxígeno unido, significa que el radical 20 será aún más nucleófilo que 17; así, este radical sustituido con oxígeno (20) se considera fuertemente nucleófilo.

Existe una forma adicional de ver la interacción frontera-orbital entre un alqueno y un radical centrado en carbono. Comprender esta visión alternativa comienza recordando que la mayor interacción frontera-orbital entre un radical centrado en carbono y un compuesto insaturado es entre el SOMO del radical y el orbital π* (LUMO) del alqueno (Figuras 5-7). Dado que la interacción SOMO-LUMO es la más importante y dado que cualquier donación de electrones en el estado de transición resultante de esta interacción debe implicar la transferencia de electrones desde el SOMO (el LUMO no tiene electrones para transferir), el radical está actuando como donante de electrones y, por lo tanto, se está comportando como un núcleo phile. ²⁹

2. Radicales electrofílicos

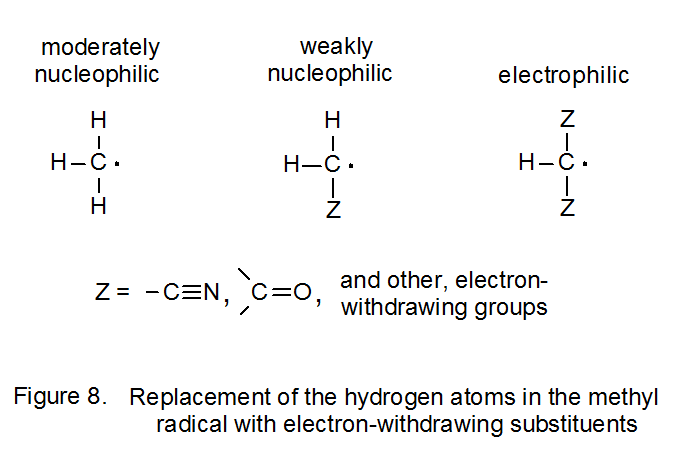
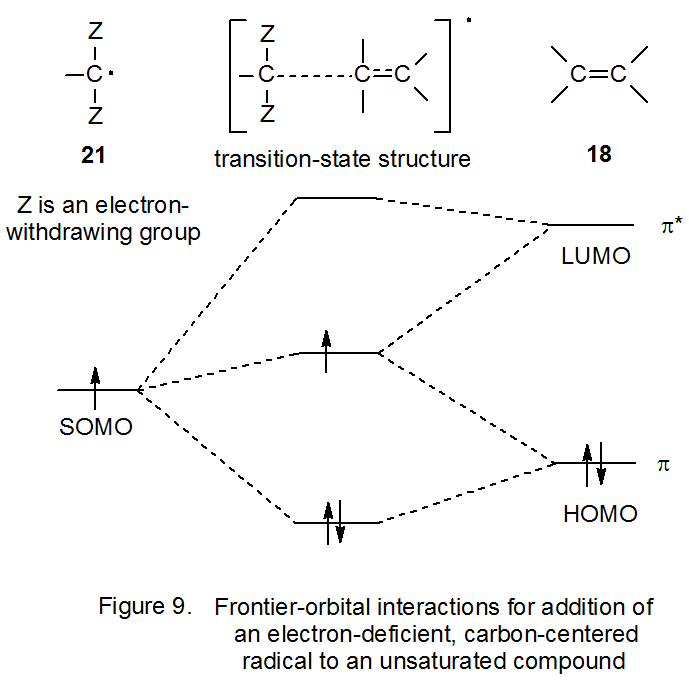
Si un átomo de hidrógeno unido a un radical centrado en carbono se reemplaza por un sustituyente aceptor de electrones (por ejemplo, un grupo ciano o carbonilo), el radical resultante se vuelve más electrófilo. ^6,18,30,31 La sustitución adicional de este tipo aumenta aún más la electrofilicidad radical (Figura 8). El grupo aceptor de electrones hace que el nivel de energía asociado con el orbital molecular ocupado individualmente del radical sustituido se mueva a una posición más baja en energía; es decir, el radical se vuelve más estable. ^6,32 Cuando el nivel de energía de un SOMO en un radical centrado en carbono se vuelve suficientemente bajo, la interacción mayor frontera-orbital con un alqueno cambia; es decir, la interacción primaria ya no es con el orbital π* del alqueno sino con su orbital π (Figura 9). Cuando se produce este cambio, el desplazamiento primario en la densidad electrónica en el estado de transición se aleja del HOMO lleno hacia el SOMO parcialmente lleno; así, el radical es electrófilo.

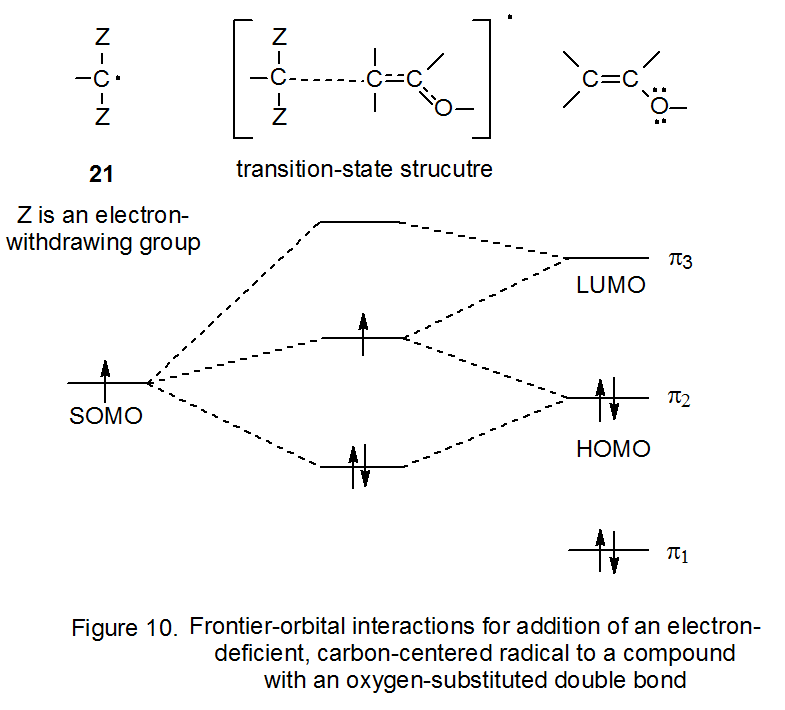
La Figura 10 representa la interacción frontera-orbital del radical 21 con un alqueno que tiene un sustituyente donador de electrones. Dado que el HOMO para el alqueno sustituido (Figura 10) es mayor en energía que el HOMO del alqueno no sustituido (Figura 9), ²⁸ estabilización en estado de transición a partir de la interacción SOMO-HOMO será mayor para la reacción que involucra al alqueno sustituido (Figura 10). Debido a esta mayor estabilización, el radical 21 reacciona más rápidamente con el alqueno más rico en electrones, comportamiento esperado de un intermedio electrófilo.

C. Equilibrio de los efectos polares y de entalpía

La discusión al inicio de este capítulo se centró en grupos de reacciones similares que obedecen a la relación Evans-Polanyi, es decir, reacciones en las que las energías de activación pueden determinarse a partir de entalpías de reacción usando la ecuación 1. La atención luego se volvió hacia reacciones donde esta relación simple (eq 1) no se sostiene. Las energías de activación para reacciones que no obedecen a la relación Evans-Polanyi están influenciadas por efectos polares operativos en el estado de transición. Dado que algunas reacciones están más sujetas a efectos de entalpía y otras a efectos polares, surge naturalmente la pregunta de cuál es el equilibrio entre estas dos. El análisis de componentes principales responde a esta pregunta con el hallazgo de que “los factores dominantes que influyen en las reacciones de adición de radicales son los efectos polares solos para radicales fuertemente nucleófilos o fuertemente electrofílicos... y los efectos de entalpía solos para radicales débilmente nucleofílicos o débilmente electrófilos”. ¹⁸ Para los radicales moderadamente nucleofílicos o moderadamente electrofílicos son importantes tanto los efectos polares como los de entalpía. ¹⁸