VI. Constantes de velocidad para la abstracción de átomos de hidrógeno por radicales de carbohidratos

Última actualización
Guardar como PDF

Page ID: 79609

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

A. Extrapolación de los resultados de los radicales modelo

La filicidad radical se encontró primero en este capítulo en las reacciones de compuestos orgánicos simples (Sección I.B). Se supuso que la información sobre la reactividad de estos compuestos podría extrapolarse a otros más complejos, específicamente a carbohidratos. Los datos experimentales apoyaron la validez de esta suposición al proporcionar ejemplos de reacciones de radicales carbohidrato que comparaban cualitativamente a las de radicales más simples. Por ejemplo, las reacciones en la ecuación 2 mostraron que el radical ciclohexilo (un modelo de carbohidratos) era nucleófilo porque se sumaba más rápidamente a enlaces múltiples deficientes en electrones que a los ricos en electrones. ⁶ Se observó un comportamiento nucleofílico similar en las reacciones del radical carbohidrato 26 (Esquema 2). En otro ejemplo, las reacciones descritas en las ecuaciones 4 y 5 para moléculas orgánicas simples mostraron que la coincidencia de polaridad incrementó la tasa de abstracción de átomos de hidrógeno. Extender la coincidencia de polaridad a los radicales carbohidrato ofreció una justificación para que el radical electrófilo 22 abstrayera un átomo de hidrógeno rico en electrones más rápidamente que uno deficiente en electrones (Esquema 1). Existe, por supuesto, una limitación a la extrapolación de los resultados obtenidos de radicales simples a radicales que son más complicados. Identificar una limitación, como se hace en la siguiente sección, puede ser útil y puede conducir a una mayor comprensión de la reactividad del radical más complicado.

B. Una limitación en la extrapolación de la reactividad del radical alquilo a los radicales carbohidrato

La extrapolación de los resultados de reacciones de intermedios estructuralmente simples a veces proporciona la única información disponible para juzgar la reactividad de otros más complejos. La extrapolación exitosa genera confianza en los modelos seleccionados, pero como los sistemas modelo por su propia naturaleza tienen limitaciones, dicha extrapolación siempre está sujeta a cierta incertidumbre. La reacción mostrada en la ecuación 9 ilustra la necesidad de precaución al proyectar la reactividad de un radical simple a uno más complejo. Los datos de la Tabla 2 muestran que las constantes de velocidad para la abstracción de átomos de hidrógeno a partir de compuestos con enlaces H-Sn, H-S y H-Si son esencialmente independientes de si el radical de abstracción es primario, secundario o terciario. (Los factores estéricos tienen poco efecto sobre las constantes de velocidad para la abstracción de hidrógeno. ⁴¹) Extendiendo este patrón de reactividad a compuestos con enlaces H—Se y sabiendo que la constante de velocidad para la abstracción de átomos de hidrógeno a partir de C ₆ H ₅ SeH por el radical primario 27 es 2.1 x 10 ⁹ ^M-1 s ^-1 a 25 ^o C ¹⁴ lleva a la predicción de que la constante de velocidad para la reacción del radical piranos-1-ilo 9 con C ₆ H ₅ sEH debería tener un valor similar. No lo hace; el valor es mucho menor (3.6 x 10 ⁶ M ^‑1 s ^-1 a 78 ^o C). ¹⁵

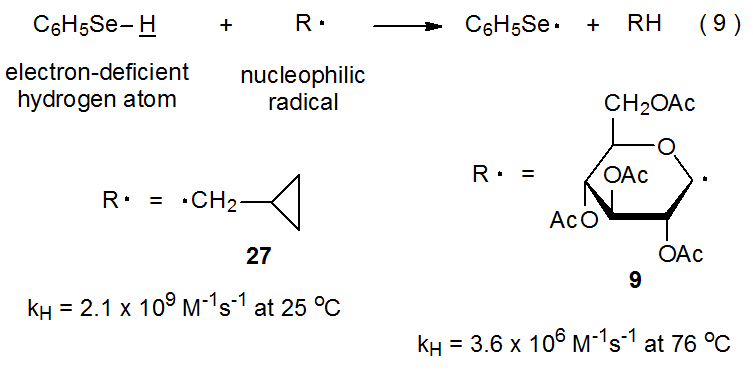(9) .png

C. Una explicación para la extrapolación infructuosa: pérdida de estabilización del estado de transición

Al tratar de comprender la constante de velocidad menor de lo esperado para la abstracción de átomos de hidrógeno por el radical 9, es útil recordar del Capítulo 6 (Sección IV.A.2.c) que la conformación de los radicales piranos-1-ilo depende del efecto cuasianomérico, es decir, de la estabilización interacción del orbital σ* del enlace _C2-O con los orbitales de tipo p en el átomo de oxígeno del anillo y C-1. Este efecto es lo suficientemente potente como para hacer que 9 adopte la conformación de barco, por lo demás inestable, mostrada en la Figura 12. Dado que la estabilización cuasianomérica solo puede existir en sistemas estructuralmente complejos, los radicales simples están limitados en su capacidad para modelar radicales piranos-1-ilo. El efecto cuasianomérico proporciona una base para comprender el valor menor de lo esperado para la constante de velocidad para la abstracción de átomos de hidrógeno por el radical 9.

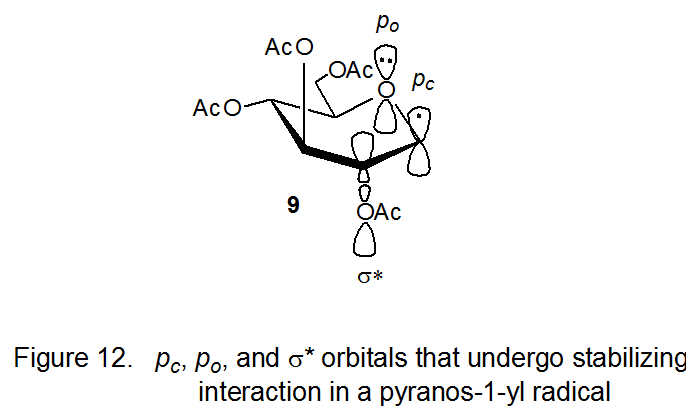
A medida que la reacción de abstracción de átomos de hidrógeno mostrada en la ecuación 9 (R· = 9) se mueve hacia el estado de transición, las interacciones orbitales (Figura 12) que provocan la deslocalización de electrones que estabiliza al radical 9 están desapareciendo. (Se han ido totalmente cuando se alcanza el producto.) Esta pérdida de estabilización significa que la energía de activación para la abstracción de átomos de hidrógeno en 9 será mayor que la del radical 27, para lo cual no hay una reducción comparable en la deslocalización de electrones a medida que avanza la reacción. ¹⁵ La abstracción de átomos de hidrógeno, en efecto, obliga a una localización electrónica que provoca una pérdida de estabilización para el radical deslocalizado 9 pero no para el localizado 27. Esta disminución en la estabilización en el estado de transición para la reacción de un radical piranos-1-ilo reduce su constante de velocidad para la abstracción de átomos de hidrógeno.

La propuesta de que la pérdida en estado de transición de estabilización cuasianomérica en los radicales piranos-1-ilo es responsable de su reducida capacidad de abstracción de hidrógeno conlleva la predicción de que los radicales carbohidrato que no están tan estabilizados deberían tener mayores constantes de velocidad para la abstracción de átomos de hidrógeno. La información cuantitativa necesaria para evaluar esta predicción no existe, pero sí hay información cualitativa que sustenta la idea básica. Como se menciona en la Sección V del Capítulo 6, los radicales piranos-1-ilo pueden generarse y observarse en tolueno o tetrahidrofurano, pero los radicales centrados en C-2, C-3 o C-4 (sin átomo de oxígeno unido al centro radical y, por lo tanto, no es posible una estabilización cuasianomérica) no se pueden observar en estos solventes porque tales radicales abstraen rápidamente los átomos de hidrógeno del solvente. (Solo se observan radicales α-tetrahidrofurilo en reacciones realizadas en tetrahidrofurano y solo se detectan radicales bencilo en reacciones en tolueno. ⁴²)

La posibilidad de que una pérdida de estabilización del estado de transición debido a la disminución de la deslocalización sea responsable de una constante de velocidad menor de lo esperado para la abstracción de átomos de hidrógeno por un radical piranos-1-ilo conduce a la propuesta de que una pérdida similar de estabilización debería tener un efecto similar sobre el hidrógeno- abstracción de átomos por otros radicales. Las constantes de velocidad para la abstracción de C ₆ H ₅ SH inciden en esta propuesta. Los radicales primarios, secundarios y terciarios simples tienen constantes de velocidad para la abstracción de átomos de hidrógeno de C ₆ H ₅ SH cerca de 1 x 10 ⁸ M ^-1 s ^-1 a 25 ^o C (Tabla 2), pero la constante de velocidad para la abstracción de este tiol por el radical bencilo es mucho más pequeño (3.13 x 10 ⁵ M ^‑1 s ^-1 25 ^o C). ¹³ Debido a que el radical bencilo pierde estabilización de resonancia a medida que tiene lugar la abstracción de átomos de hidrógeno, se esperaría que paralelamente al radical piranos-1-ilo en tener una abstracción de átomos de hidrógeno constante de velocidad menor que la 1 x 10 ⁸ M ^-1 s ^-1 observada para radicales no estabilizados. El hecho de que la constante de velocidad para la abstracción de átomos de hidrógeno por el radical bencilo (3.13 x 10 ⁵ M ^‑1 s ^-1) sea sustancialmente menor que 1 x 10 ⁸ M ^-1 s ^-1 fortalece la explicación de deslocalización decreciente para reducir reactividad del radical piranos-1-ilo 9.